9. Энтропия и беспорядок

Первое начало термодинамики, представленное нами в предыдущей главе, выдвигает на передний план важный запрет: невозможность создания энергии. Настало время рассмотреть второе начало термодинамики, которое выдвигает другой, не менее строгий запрет: невозможность создания порядка. Мы должны будем дать точное определение понятию порядка, введя связанную с ним физическую величину – энтропию. Мы увидим, что невозможно создать порядок в одном месте, не уменьшив его одновременно в другом. Например, создание компьютера, в высшей степени упорядоченной системы, не может произойти без увеличения хаоса на Земле. Мы откроем неизбежное трагическое последствие: необратимый характер любых наших действий, которые неотвратимо увеличивают хаос во Вселенной без всякой возможности вернуться назад.

1. Неизбежное увеличение хаоса

Что такое энтропия?

Энтропия понятие довольно сложное и вместе с тем исключительно полезное, ибо она является ценнейшим источником информации для понимания некоторых необратимых процессов во Вселенной.

Чтобы ее понять, мы понаблюдаем за естественным изменением тела, которому не будет сообщаться никакой энергии: энергия тела остается постоянной, но это не означает, что ничего не происходит. В термодинамике тело, которое не обменивается материей и энергией с внешней средой, называется изолированным.

Первый опыт

Перенесемся в космический корабль, в котором шлюзовая камера отделяет отсек с воздухом от отсека с вакуумом. Когда мы откроем шлюзовую камеру, воздух хлынет во второй отсек и поспешит заполнить все уголки доступного ему пространства. Причина этого в том, что молекулы воздуха испытывают толчки сзади (оттуда, где есть воздух), но не спереди (оттуда, где воздуха нет), – эти толчки вытесняют их в безвоздушное пространство, которое ими наполнится.

Вывод: газ стремится заполнить любое пустое пространство. И наоборот: чтобы его сжать и уменьшить его объем, необходимо проделать некоторую работу (нужна внешняя сила, которая переместит текучую среду, а если есть «сила» и «перемещение», значит, есть и «работа»). Но в этом случае тело перестает быть изолированным, поскольку мы придаем ему энергии с помощью работы.

С другой стороны, объем жидкости или твердого тела не меняется или меняется очень мало, потому что молекулы уже находятся в контакте друг с другом (сжатое состояние).

Итак, запомним: «как правило, объем изолированного тела не может уменьшиться, а может только увеличиваться или оставаться постоянным».

Второй опыт

Толкнем какой-нибудь предмет так, чтобы он проскользил по полу. В конце концов он остановится сам по себе. Если мы считаем, что система (пол+предмет) не взаимодействует ни с чем другим, общая энергия должна сохраняться: мы видели, что на практике она становилась микроскопической (повышение температуры).

Чтобы понять, что происходит на микроскопическом уровне, необходимо знать, что молекулы перемещаются каждое мгновение в самых разных направлениях с разной скоростью. Например, температура 20 °C указывает, что молекулы обладают определенной средней кинетической энергией, но каждая из молекул обладает разной скоростью: некоторые не двигаются, другие перемещаются со скоростью 10 м/с, третьи со скоростью 100 м/с и так далее.

На практике бесконечные столкновения вызывают постоянный обмен энергией между молекулами, которые то ускоряются, то тормозят, что объясняет разницу их скоростей.

Таким образом, столкновения приводят к совершенно хаотичному обмену энергией между молекулами и стремятся придать им такие же случайные направления. В нашем предмете, скользящем по полу, основное направление движения молекул сосредоточено в системе отсчета пола (движения по нему): столкновения с полом постарались восстановить равновесие между различными направлениями. В каком-то смысле молекулы, двигаясь в среднем быстрее в направлении движения объекта, претерпели столкновения более сильные, которые сильнее их затормозили.

В конечном итоге кинетическая энергия молекул сохранилась, но общее движение прекратилось: макроскопическая энергия исчезла и превратилась в микроскопическую.

Результат будет таким же для любого движения между двумя телами (например, для двух газов, которые двигаются относительно друг друга). В любом случае макроскопическое движение одного тела относительно другого стремится уменьшиться в пользу беспорядочного микроскопического движения молекул (повышение температуры).

Чтобы проделать обратную операцию (воссоздать макроскопическое движение), необходимо вмешательство извне (например, толкнуть объект). Но в этом случае система (пол+предмет) получает энергию и перестает быть изолированной.

Запомним: в основном температура изолированного тела не может уменьшаться, она может только увеличиваться или оставаться постоянной.

Первые выводы

Подведем итоги этих двух опытов.

• Объем изолированного тела обычно стремится к увеличению. Это значит, что молекулы стремятся занять как можно больше места в пространстве. Если мы заинтересуемся одной определенной молекулой, будет очень трудно узнать, где именно она находится, поскольку ее придется искать в более широком пространстве. По аналогии с повседневной жизнью, мы скажем, что «беспорядок» увеличился (молекулы больше не сосредоточены в ограниченном пространстве).

• Температура изолированного тела обычно стремится к повышению. Это значит, что молекулы стараются приобрести как можно больше различных скоростей: действительно, повышенная температура говорит о том, что некоторые молекулы двигаются очень быстро, но другие продолжают двигаться медленно. В каком-то смысле набор скоростей молекул увеличивается, когда повышается температура. Можно сказать, что «беспорядок» усилился: на этот раз речь идет о хаосе скоростей, а не расположения.

Два первых опыта показывают, что хаос в изолированной системе может только увеличиваться.

Третий опыт

Представим формирующуюся планету. Предположим, что огромное количество газа равномерно распределено вокруг рождающейся планеты. Под действием гравитации газ будет притянут планетой: приближаясь к планете, он будет сгущаться. Молекулы будут скапливаться рядом с поверхностью планеты, что будет создавать давление вверх, компенсирующее гравитацию. Как и на Земле, когда равновесие будет достигнуто, давление у поверхности будет больше, чем на высоте.

В процессе этих трансформаций общая энергия тела сохранилась. И действительно, планета, конечно, проделывает работу относительно газа, но это лишь уменьшает потенциальную энергию газа в пользу его кинетической энергии (как в отношении мяча, который падает). Другими словами, речь идет о «консервативной работе».

Таким образом, мы констатируем, что газ сгустился сам по себе, мы не придавали ему энергии. В опыте 1 мы указали, что обычно объем газа стремится увеличиться, если нет притока энергии. Здесь мы видим, что так происходит не всегда.

Но интересно то, что первоначальная потенциальная энергия газа превратилась в микроскопическую кинетическую (макроскопическая энергия равна нулю, поскольку газ достиг равновесия), – иначе говоря, температура повысилась.

В опыте 2 мы показали, что температура тела стремилась к повышению при отсутствии обмена энергией, – это же мы наблюдаем в опыте 3.

В действительности в третьем опыте все происходит так, словно газ «разрывается» между двумя противоположными «устремлениями»: с одной стороны, он хочет увеличиться в объеме (даже если понизится температура), с другой – повысить температуру (даже если уменьшится объем). Если он выберет второй путь, значит, «желание» увеличить температуру больше «желания» увеличить объем.

ОПРЕДЕЛЕНИЕ ЭНТРОПИИ

Чтобы более точно определить понятие энтропии, рассмотрим на микроскопическом уровне поведение газа, в котором (условно) всего четыре молекулы: красная, зеленая, синяя и желтая.

Предположим, что эти молекулы помещены в некое огороженное пространство, которые мы мысленно поделим на четыре части (см. схему ниже). Мы не берем в расчет гравитацию. Столкновения между молекулами приводят к тому, что они занимают все ячейки пространства. Если мы в определенный момент сфотографируем огороженное пространство, где мы увидим молекулы?

Из-за толчков любое положение равновероятно: мы привели два примера на схеме.

Слева все молекулы находятся в одной зоне. Подобных расположений может быть четыре, поскольку пространство поделено на четыре зоны.

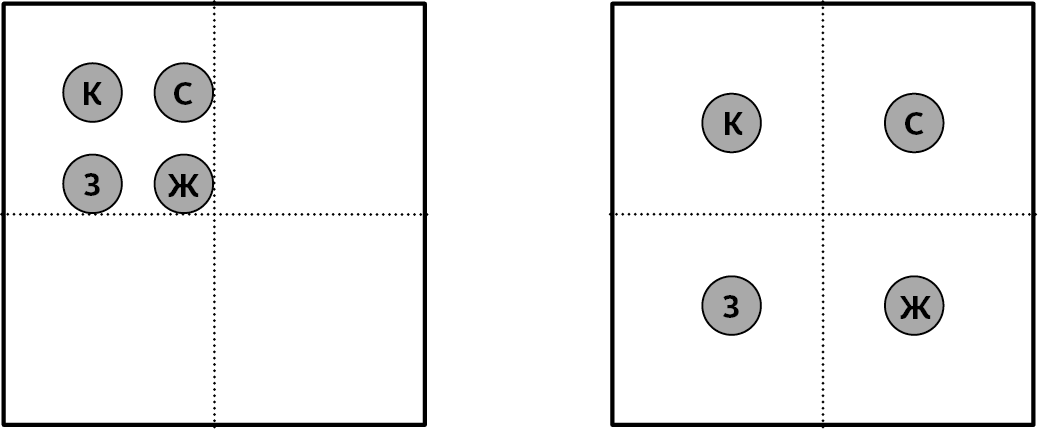
На схеме справа, напротив, в каждой зоне по одной молекуле. Сколько же может быть подобных комбинаций?

В таблице ниже мы приведем все возможные примеры того, как молекулы могут располагаться в четырех разных зонах: цифра соответствует номеру зоны, в которой находится молекула. Каждая строчка представляет новое расположение.

В шести указанных комбинациях каждая молекула находится в отдельной зоне. Здесь представлены варианты, когда красная молекула всегда в зоне № 1. Мы можем привести примеры, когда она будет в зонах 2, 3 и 4. Итого это даст 24 различные комбинации.

Сравним это с четырьмя вариантами, когда все молекулы сосредоточены в одной зоне. Поскольку каждый вариант одинаково возможен, это значит, что гораздо больше вероятности обнаружить молекулы рассредоточенными по всему пространству, чем сгруппированными в одном углу.

В реальности газ содержит огромное количество молекул в значительном объеме, так что предыдущий результат можно существенно дополнить. Если мы сделаем снимок в определенный момент, со 100-процентной уверенностью можно сказать, что молекулы будут равномерно распределены по всему пространству. Это установилось равновесие на макроскопическом уровне.

Таким образом, оперируя статистическими терминами, мы обнаруживаем, что газ стремится равномерно распределиться по всему доступному ему пространству.

Символом Ω обозначается число расположений молекул: формула энтропии выглядит как S = k ⋅ ln(Ω) (где k – постоянная Больцмана, уже упоминавшаяся в главе 8). Изолированный газ стремится занять все возможные позиции равновероятным способом: то есть энтропия S стремится к увеличению до тех пор, пока не достигнет максимума при равновесии.

В предыдущем примере мы рассматривали только расположение молекул, но мы можем провести точно такие же рассуждения относительно их скоростей. Предположим, что общая энергия газа равна U и состоит только из кинетической энергии молекул. Как она распределяется между разными молекулами? Необходимо снова пересмотреть все конфигурации, при которых общая энергия молекул равна U. И тогда можно продемонстрировать, что распределение молекул в зависимости от их скорости будет следующей:

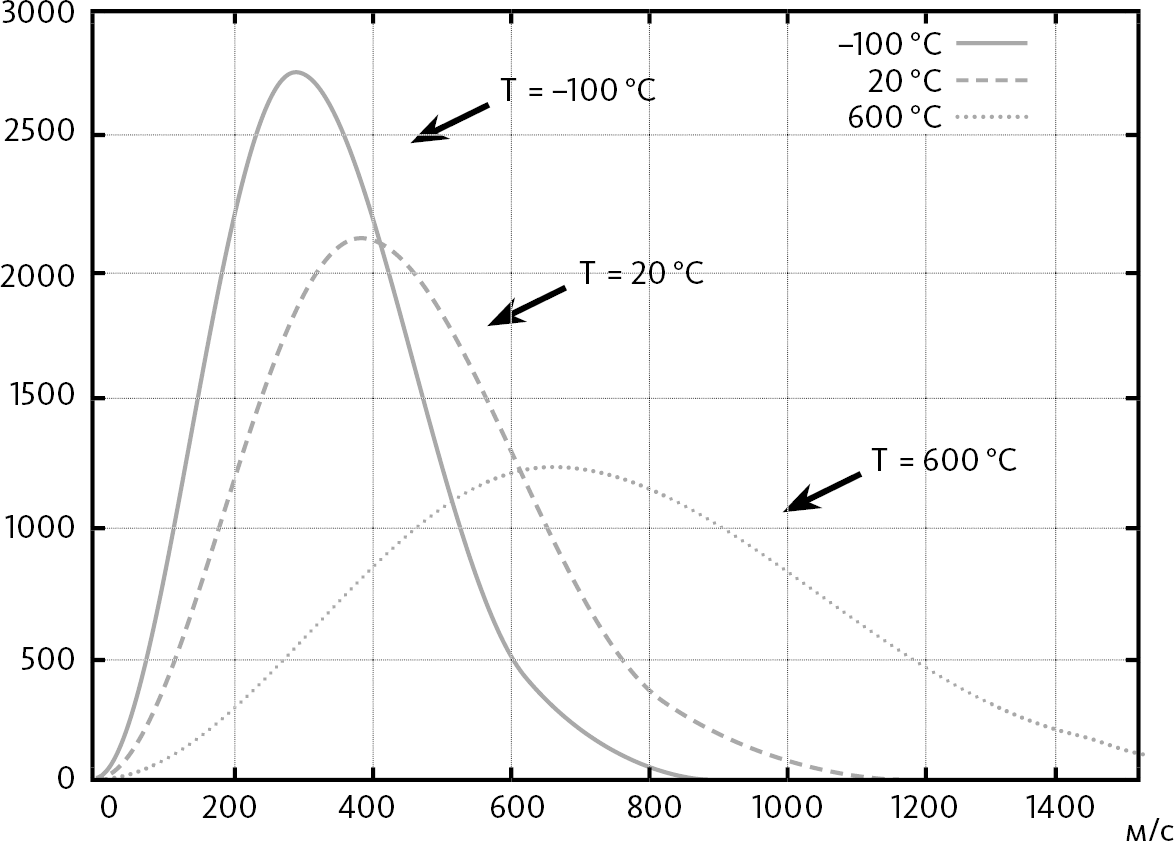
Эти кривые показывают, что некоторые скорости дают особый результат. Например, при температуре T = –100 °C многие молекулы двигаются со скоростью 300 м/с. Чем выше температура, тем выше эти особые скорости, что логично, поскольку температура связана со средней кинетической энергией молекул.

С другой стороны, мы видим, что скорости движения молекул сильно отличаются друг от друга: при T = –100 °C диапазон скоростей составляет примерно от 0 до 800 м/с. При T = 600 °C диапазон скоростей от 0 до 1600 м/c. Мы видим, что чем выше температура, тем больше разброс скоростей молекул. Именно об этом мы говорили в самом начале данной главы.

Мы определили энтропию в виде S = k ⋅ ln(Ω), где Ω – количество вариантов не только расположений, но и скоростей молекул. Чем больше объем, тем больше вариантов позиций. Чем выше температура, тем больше вариантов скоростей.

Во всех случаях энтропия изолированной системы может только увеличиваться (общее количество конфигураций стремится к постоянному увеличению).

Уточним: когда уменьшается объем, уменьшается «беспорядок» в распределении молекул. Но когда повышается температура, «беспорядок» в скоростях молекул усиливается. Можно продемонстрировать, что во время этого действия «усиление беспорядка» из-за температуры интенсивнее, чем «уменьшение беспорядка» из-за объема: в совокупности беспорядок усиливается.

На практике изолированное тело всегда выбирает путь, который увеличивает беспорядок.

Обобщение

Такое понятие беспорядка может показаться неопределенным и расплывчатым; на самом деле можно дать более точное определение беспорядка, но оно будет довольно сложным. Именно поэтому мы вынесли его во врезку выше.

Достаточно запомнить, что бесчисленные столкновения влекут за собой самое беспорядочное распространение энергии тела: мы неотвратимо стремимся к распространению всеобщего беспорядка. На деле этот беспорядок проявляется в распределении молекул (увеличение объема) и их скоростей (повышение температуры).

Слову «беспорядок» физики предпочитают термин «энтропия», и мы видим, что это понятие в основном связано с объемом и температурой тела.

Запомним: При отсутствии обмена энергией с внешней средой энтропия тела неизбежно увеличивается. Она достигает максимума, когда достигнуто равновесие».

Это составляет второе начало термодинамики.

Последствия увеличения энтропии

В качестве примера изолированной системы мы можем взять саму Вселенную: она изолирована по определению, потому что включает в себя все, что существует. Согласно рассуждениям в предыдущем параграфе, энтропия Вселенной может только увеличиваться.

Фактически там, где есть уменьшение объема (например, формирование планет и звезд), оно сопровождается повышением температуры. С другой стороны, если энтропия локально уменьшается (например, охлаждение без потери объема), это обязательно увеличивает энтропию в другом месте, по меньшей мере в таком же количестве.

Например, энтропия внутри холодильника уменьшается, когда мы его включаем, но это нагревает комнату. На деле увеличение энтропии комнаты больше, чем уменьшение энтропии холодильника. То есть общая энтропия увеличивается.

ФЕНОМЕН РАССЕЯНИЯ

Испеките пирог в печи. Его запах заполнит все помещение. Однако воздух выглядит неподвижным. Как же пахучие молекулы распространились по комнате?

Из-за столкновений каждая молекула газа имеет самую хаотичную траекторию. Сначала пахучие молекулы были сконцентрированы возле печи, но такая ситуация соответствует очень слабой энтропии, потому что молекулы далеки от того, чтобы занимать все возможные позиции в доступном для них пространстве. Мало-помалу из-за столкновений распространение молекул стремится стать равномерным, между тем растет энтропия газа.

Таким образом, рассеяние одного газа в другом является прекрасным примером роста энтропии путем увеличения объема. В человеческом теле или в компьютере, напротив, каждая молекула удерживается удерживается на определенном месте, что и позволяет всей системе функционировать… Это значит, что в подобных строго структурированных системах необходимо бороться против естественного стремления молекул заполнить собой все пространство, что привело бы к формированию однородного сгустка, лишенного всякой функциональности. Чуть позже мы вернемся к средствам, с помощью которых человеческое тело способно поддерживать столь слабую энтропию.

Термическая диффузия является очень похожим примером такого рассеяния: ваша батарея обогревает всю комнату, хотя никакого движения воздуха не наблюдается. На самом деле рядом с батареей молекулы воздуха двигаются быстрее, чем где-либо, то есть это еще один пример недостаточно высокой энтропии. Благодаря столкновениям повышенная кинетическая энергия будет распространяться от одной молекулы к другой до тех пор, пока температура в комнате не станет везде одинаковой. Следовательно, энтропия достигла максимума.

Таким образом, что бы вы ни делали, вы увеличиваете энтропию вокруг себя. Это происходит, даже когда вы лежите и ничего не делаете. Ваше тело с его температурой 36,6 °C постоянно нагревает атмосферу.

Аналогично этому технические работники собирают компьютеры, локально уменьшая энтропию: материя здесь строго упорядочена, и различные молекулы не смешиваются хаотичным образом по всему пространству. Однако во время сборки техники невольно нагревают воздух: во время сборки компьютера общая энтропия значительно возрастает.

Значит ли это, что глобальное потепление неизбежно? Так было бы, если бы Земля являлась изолированным объектом, но, к счастью, в космосе происходят постоянные переносы энергии. На практике радиация стремится удалить энтропию, созданную на Земле. Это значит, что для того, чтобы остановить глобальное потепление, необходимо как можно больше энтропии отправить в космос, облегчив путь радиации.

Однако газы, создающие парниковый эффект, как раз стремятся изолировать Землю от космоса, создавая экран, препятствующий распространению земного излучения. По этой причине остановить глобальное потепление можно прежде всего сокращением выброса парниковых газов. Это сделало бы Землю менее изолированной и позволило бы энтропии, которую мы неизбежно создаем, легче уходить в космос…