3. Возвращение к сохранению энергии

Пример системы двух планет

В предыдущей главе мы сказали, что общая энергия изолированного объекта сохранялась. Чтобы показать, что этот результат не столь очевиден, как кажется, возьмем для примера две планеты («темную» и «светлую»), которые изолированы в межпланетном пространстве.

Никакая внешняя сила не действует на эту систему из двух планет (принцип изолированной системы), то есть никакая внешняя работа не применяется. Согласно выражению ΔE = A_NC напрашивается поспешный вывод о том, что энергия не меняется. Однако благодаря выражению ΔE_k = A следует также сделать вывод, что нет изменения кинетической энергии. В то же время, если мы поместим наши планеты друг против друга, они будут притягиваться, и их кинетическая энергия увеличится (➙ рис. 8.6). Значит, в наших рассуждениях где-то содержится ошибка.

На самом деле в выражении ΔE_C = A A представляет собой работу, которая применяется к обеим планетам, то есть работа, действующая на темную планету, плюс работа, действующая на светлую. Сюда входит работа внешних сил и работа внутренних сил. Однако темная планета испытывает работу, которая является результатом силы притяжения светлой планеты. В свою очередь, и светлая планета подвержена работе благодаря темной планете.

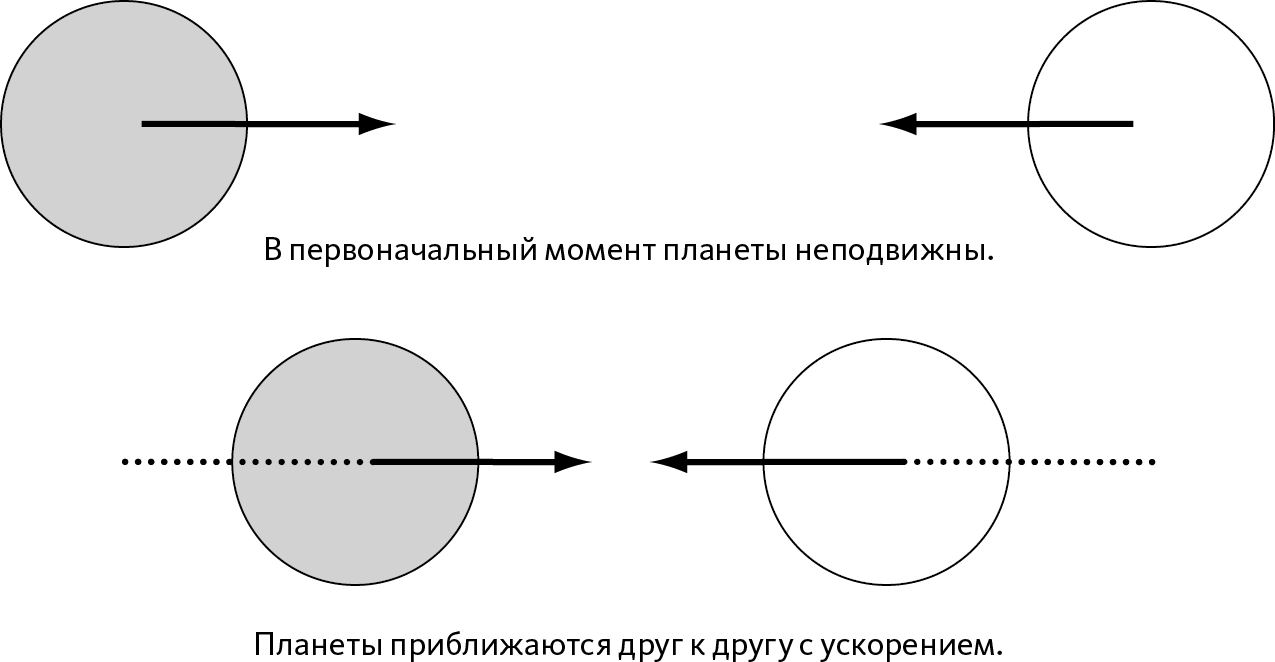
Рис. 8.6 – Притяжение между двумя планетами

Две силы противоположны друг другу, но обе они создают положительную механическую работу, то есть общая сила равна нулю, но общая работа не равна нулю. Это объясняет, что кинетическая энергия системы увеличивается, несмотря на то что она изолирована от всякого внешнего воздействия.

В противоположность тому, что можно было бы подумать, работа темной планеты по отношению к светлой не противоположна работе светлой по отношению к темной: сумма обеих работ не равна нулю.

Наличие ненулевой общей работы A указывает, что в системе есть изменение кинетической энергии ΔE_k.

Это легко проверить с помощью рис. 8.6: силы, действующие на каждую из планет, противоположны (принцип взаимодействия), но перемещение планет также происходит в противоположных направлениях. Таким образом, мы имеем дело с двумя случаями механической работы (сила, способствующая перемещению), то есть с положительной работой, а сумма двух положительных работ не может равняться нулю.

Потенциальная энергия взаимодействия

Остается понять, почему общая энергия системы сохраняется, в отличие от общей кинетической энергии.

Ни для одной из отдельно взятых планет мы не можем определить потенциальную энергию. В самом деле, каждая планета испытывает действие силы тела, которое не является неподвижным, то есть не соблюдается критерий, согласно которому можно было бы определить потенциальную энергию.

В свою очередь, общая работа, осуществляемая двумя силами, зависит только от расстояния между двумя планетами (это легко продемонстрировать математически). Таким образом, если планеты перейдут от расстояния d₁ к расстоянию d₂, общая работа будет такой же, независимо от пройденного пути от d₁ к d₂. То есть мы можем присвоить системе из двух планет вполне вычисляемую «потенциальную энергию», которая зависит лишь от расстояния между двумя объектами.

Эта общая потенциальная энергия двух взаимодействующих тел называется просто гравитационной энергией. Необходимо хорошенько усвоить, что, если потенциальная энергия системы определена таким образом, потенциальные энергии одной и другой планеты по отдельности не имеют никакого смысла.

В конечном итоге работа, не зависящая от пройденного пути, является консервативной: она сохраняет общую энергию системы двух планет. Увеличение общей кинетической энергии сопровождается автоматическим равноценным уменьшением потенциальной энергии взаимодействия.

Внешняя и внутренняя работа

Вывод о гравитационном взаимодействии аналогичен выводу о электростатическом взаимодействии (мы помним о сходстве двух этих сил). Между тем объект, каким бы он ни был, состоит из миллиардов и миллиардов атомов или молекул, находящихся в электростатическом взаимодействии. Это взаимодействие распространяет во все стороны разные силы, то есть огромное количество работы, которая действует на каждую молекулу. Но эта внутренняя работа объекта является консервативной: общая внутренняя работа, конечно, не равна нулю, но она проявляется в виде изменения микроскопической потенциальной энергии.

То есть внутренняя работа не меняет общую энергию объекта, поскольку является консервативной (ΔE = A_NC = 0). С другой стороны, она может менять кинетическую энергию объекта (ΔE_k = A≠ 0).

Например, во время химической реакции происходит перегруппировка молекул, что меняет потенциальную микроскопическую энергию вещества (действие электростатической работы). Это может повлечь за собой увеличение микроскопической кинетической энергии вещества (повышение температуры). Кинетическая энергия увеличилась за счет потенциальной: общая энергия сохранилась.

Запомним: Изменение общей энергии объекта является результатом только неконсервативной работы внешних сил, потому что внутренняя работа всегда консервативна. В частности, если объект является изолированным, его энергия сохраняется.

СОХРАНЕНИЕ ЭНЕРГИИ В МАТЕМАТИЧЕСКИХ ТЕРМИНАХ

Если работа всех сил не зависит от пройденного пути, значит, мы можем говорить о потенциальной энергии, как ΔE_p = –A. Поскольку ΔE_k = A, из этого следует, что ΔE_k = –ΔE_p. Мы убеждаемся в том, что потенциальная энергия изменяется противоположно изменению кинетической. Следовательно, ΔE_k + ΔE_p = 0, или ΔE = 0: общая энергия сохраняется.

В этом же мы могли убедиться, рассматривая выражение ΔE = A_NC. Общая работа является консервативной: A_NC = 0, то есть ΔE = 0.

СЛЕДУЕТ ЗАПОМНИТЬ

• Мощность является способностью силы увеличивать кинетическую энергию объекта за одну секунду. Она зависит от силы, ее направления и скорости объекта и выражается в ваттах.

• Работа является способностью силы увеличивать кинетическую энергию объекта за определенный отрезок времени. Она зависит от силы, ее направления и расстояния, пройденного объектом. Выражается в джоулях.

• Если работа, проделанная силой, не зависит от пройденного пути, мы можем определить потенциальную энергию, связанную с этой силой. В этом случае данная сила не меняет общую энергию объекта, поскольку увеличение кинетической энергии сопровождается уменьшением потенциальной. Такую силу называют консервативной.

• Изменение кинетической энергии объекта равно общей работе задействованных сил (как внешних, так и внутренних по отношению к объекту).

• Изменение общей энергии объекта равно общей работе внешних неконсервативных сил. Работа внутренних сил всегда консервативна и не меняет энергию объекта.

• Теплота является микроскопической работой объекта на молекулярном уровне, результат действия которой проявляется на микроскопическом уровне (в частности, изменение температуры).