2. Первый закон термодинамики

Консервативные и неконсервативные силы

Потенциальную энергию по-прежнему невозможно определить

Работа силы позволяет объекту приобрести кинетическую энергию. Однако мы говорили, что потенциальная энергия представляет собой кинетическую энергию, которая может себя проявить. Таким образом, между работой и потенциальной энергией существует очевидная связь.

Если кинетическая энергия способна увеличиться с 0 до E_kmax, это значит, что изначальная потенциальная энергия объекта E_kmax. Кроме того, когда объект достигнет максимальной кинетической энергии E_kmax, еще большей энергии он уже не достигнет, и его потенциальная энергия снизится до 0.

Таким образом, если кинетическая энергия E_k повышается от 0 до E_kmax, его потенциальная энергия E_p снижается с E_kmax до 0. Изменение E_p прямо противоположно изменению E_k. Поскольку ΔE_k = A, значит, ΔE_p = –A. Это та самая связь, которую мы искали между потенциальной энергией и работой.

СВЯЗЬ МЕЖДУ «НЕИЗМЕННОЙ ОКРУЖАЮЩЕЙ СРЕДОЙ» И ПРОДЕЛАННОЙ РАБОТОЙ

В предыдущей главе мы говорили, что определить потенциальную энергию можно, если окружающая среда остается неизменной. В этой главе мы говорили, что нужно, чтобы работа не зависела от пройденного пути. Совместимы ли оба этих утверждения?

Чтобы ответить на этот вопрос, необходимо вспомнить, что все силы Вселенной являются проявлением двух фундаментальных сил: гравитации и электромагнетизма. Если окружающая среда неизменна, причиной этого является электростатическая сила.

Изменение этих двух сил обратно пропорционально квадрату расстояния между объектом и притягивающим (отталкивающим) телом. В таком случае проделанная работа зависит только от изменения этого расстояния (математика очень просто это демонстрирует). Если притягивающее (отталкивающее) тело неподвижно, значит, работа зависит исключительно от изменения положения объекта. То есть работа не зависит от пути, пройденного между двумя различными точками.

Таким образом, какой бы ни была сила, если окружающая среда, которая воздействует с помощью этой силы, остается неизменной (на макро- и микроскопическом уровнях), то работа не зависит от пройденного пути, и можно определить потенциальную энергию.

Увы, если кинетическая энергия остается определенной (E_K = ½ mν²), с потенциальной все гораздо сложнее. В самом деле, мы видели в предыдущей главе, что для определения потенциальной энергии материальное окружение объекта должно оставаться неизменным. Если окружение объекта меняется, становится невозможно предсказать, какую кинетическую энергию приобретет объект, поскольку «предсказание» будет подвергнуто сомнению изменением окружающей среды.

Если окружение неизменно, можно показать, что возможное приобретение объектом кинетической энергии зависит только от его первоначальной позиции и не зависит от его скорости в этой точке (см. врезку ниже): в этой единственной точке сосредоточена точно определенная потенциальная энергия.

Представим теперь объект, который перемещается из точки А в точку В. Изменение его потенциальной энергии ΔE_p зависит только от его первоначальной позиции (А) и финальной (В). Это изменение будет одинаковым, независимо от того, какой путь прошел объект от точки А в точку В. Поскольку ΔE_p = –A, из этого следует, что работа тоже не должна зависеть от пройденного пути.

Чтобы это продемонстрировать, возьмем два разных примера.

Примеры

Пример 1. Заберемся на возвышение А и бросим с него мяч так, чтобы он упал на пол в определенной точке В. Существует множество способов бросить мяч таким образом: рис. 8.3 иллюстрирует два из них.

Земля, которая притягивает мяч, неподвижна, а это значит, что мы можем определить потенциальную энергию мяча. В связи с этим работа веса должна быть неизменной, независимо от того, какой путь пройден от А до В.

Быстрый подсчет (который мы оставим в стороне) позволяет убедиться в этом. На траектории (2) пройденное расстояние, конечно, больше, но необходимо отметить, что работа от А до D равна нулю (наполовину сила сопротивления от А до С, наполовину движущая сила от С до D). Что касается работы от D до В, можно продемонстрировать, что она равна работе от А до В (тоже изменение высоты).

Поскольку ΔE_C + A, а ΔE_p = –A, то ΔE_k + ΔE_p = 0: общее изменение энергии (кинетическая + потенциальная) равно нулю. Таким образом, мы имеем сохранение энергии.

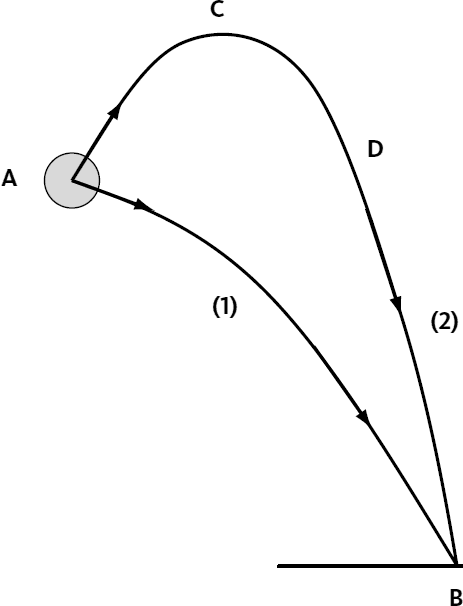
Рис. 8.3 – Мяч в свободном падении перемещается из точки А в точку В по двум разным траекториям

Пример 2. Толкнем шайбу так, чтобы она проехала по полу двумя разными путями: один прямой, а другой с двумя последовательными рикошетами (➙ рис. 8.4). Сила трения производит работу, которая заставляет шайбу терять кинетическую энергию. На этот раз окружающее пространство, оказывающее действие силы, движется (не будем забывать, что трение вызвано столкновением молекул воздуха и атомов пола с шайбой). То есть мы не можем определить потенциальную энергию шайбы.

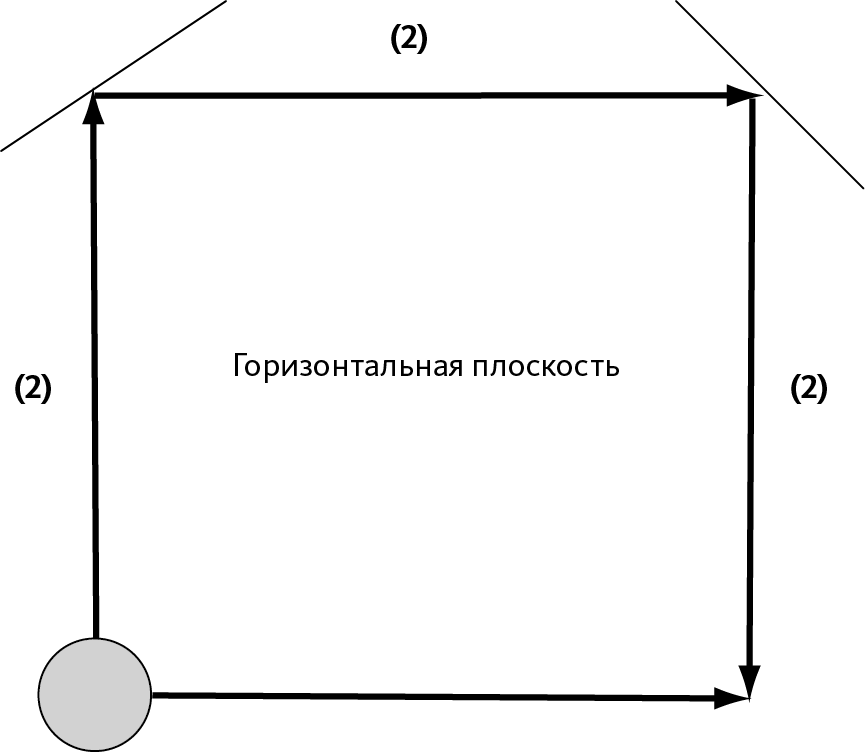
Рис. 8.4 – Путь шайбы от А до В двумя различными способами

Теперь можно легко убедиться в том, что работа силы трения зависит от пройденного пути: путь (2) втрое длиннее пути (1), и сила трения выполняет втрое большую работу.

На этот раз общая энергия шайбы отождествляется с ее кинетической энергией (потенциальная энергия отсутствует). Поскольку ΔE_k= A, а работа отрицательная (трение), это значит, что шайба теряет энергию во время движения. Сохранения энергии нет.

Три типа силы

В примере 1 мы смогли определить потенциальную энергию. Говорят, что сила тяжести происходит из потенциальной энергии. В этом случае существует сохранение общей энергии объекта, потому что «потенциальная» энергия превращается в кинетическую в процессе движения. По этой причине силу тяжести называют «консервативной» силой (она сохраняет общую энергию объекта).

Чтобы определить консервативную силу, необходимо убедиться, что ее работа не зависит от пройденного пути. Такова сила тяжести. В более общем смысле таковыми являются гравитация и электростатическая сила, когда притягивающее (или отталкивающее) тело остается неподвижным. Сюда же относится возвратная сила пружины (которая, напомним, зависит только от растяжения пружины). А также к ним относится сила инерции переноса, если система отсчета равномерно вращается вокруг неподвижной оси.

В примере 2, напротив, не была определена никакая потенциальная энергия: проделанная работа изменила общую энергию объекта, поскольку теперь она отождествляется с кинетической энергией. Это называется «неконсервативной силой».

Сила трения (твердых тел или текучей среды) – самая распространенная из неконсервативных сил. В общем случае давление также входит в эту категорию (мы не будем вводить «потенциальную энергию давления»).

Различают также и третий тип сил: те, которые не работают, то есть не меняют кинетическую энергию объекта. Таковы силы, которые всегда перпендикулярны движению: например, реакция опоры при отсутствии трения или натяжение нерастяжимой нити. Прекрасным примером этого служит сила Кориолиса (она лишь изгибает траекторию). В конце концов мы увидим, что магнетизм тоже входит в эту категорию.

Поскольку эти силы не меняют общей энергии объекта, мы можем классифицировать их консервативные силы. Однако они представляют собой совершенно особый случай, потому что соответствующая потенциальная энергия равна нулю (кинетическая энергия невозможна). Одним словом, эти силы не играют никакой роли с точки зрения энергии.

В конечном итоге изменение общей энергии объекта производят только неконсервативные силы: запишем ΔE = A_NC (NC – non conservative).

Теплота

Определение

Среди сил, упомянутых в предыдущем параграфе, некоторые возникают при взаимодействии на микроскопическом уровне. Например, сила трения есть результат электростатического взаимодействия молекул. Тем не менее влияние этих сил проявляется и на макроскопическом уровне: не обязательно брать микроскоп, чтобы увидеть, как предмет тормозит из-за силы трения.

Легко представить, что эти силы оказывают влияние и на микроскопическом уровне: переверните велосипед и попробуйте остановить рукой быстро вращающееся колесо. Вы обожжетесь. Иначе говоря, трение не только тормозит колесо, но и повышает температуру вашей руки. Это значит, что средняя кинетическая энергия молекул вашей руки увеличилась.

В физике работа силы, которая таким образом проявляет себя на микроскопическом уровне, называется теплотой и обозначается Q. То есть теплота является частным случаем работы.

В примере с колесом трение вашей руки осуществило макроскопическую работу по отношению к колесу и уменьшило макроскопическую кинетическую энергию колеса (оно затормозило). В свою очередь, трение колеса оказало на вашу руку действие теплоты, что увеличило микроскопическую кинетическую энергию вашей руки (повышение температуры).

В физике необходимо четко различать понятие теплоты (энергии, которую сила придала объекту) и понятие температуры (показатель энергии, которой обладает объект). Одним словом, положительная теплота в целом стремится повысить температуру, а отрицательная – понизить.

Пример

Чтобы внести ясность, приведем другой пример обмена энергией с помощью теплоты.

Распахните дверь своего дома среди зимы. Даже если не будет ни малейшего ветра, температура в помещении быстро начнет понижаться. Почему? Потому что даже если мы этого не видим, молекулы воздуха на улице и в помещении сталкиваются на большой скорости. Однако молекулы в помещении в среднем обладают большей кинетической энергией, чем те, что снаружи.

На рис. 8.5 показано, что происходит во время этого столкновения: более быстрая молекула придает кинетической энергии более медленной. Таким образом, действующая электростатическая сила совершила положительную работу на более медленную молекулу (придала ей ускорение) и отрицательную работу на более быструю молекулу (затормозила ее).

Эта работа производится на микроскопическом уровне, и ее последствия тоже микроскопического уровня: вырабатывается теплота. В итоге эта теплота подогрела воздух снаружи и охладила воздух внутри: произошел обмен энергией, хотя материя никак не изменилась (воздух остался на своем месте: человек в кресле вдыхает те же молекулы, хотя и более «охлажденные»).

В предыдущем примере энергия перешла из помещения на улицу с помощью теплоты. Мы предположили, что общая энергия системы сохранилась, а это значит, что теплота, переданная помещением улице, прямо противоположна теплоте, переданной улицей помещению. Однако даже если этот вывод выглядит интуитивным, он далеко не обычен.

На самом деле этот обмен энергией, уже упомянутый в предыдущей главе, достаточно важен, чтобы мы снова заострили на нем внимание. Мы еще раз уточним условия, при которых он возможен, обозначив при этом все подводные камни, которые следует обойти.

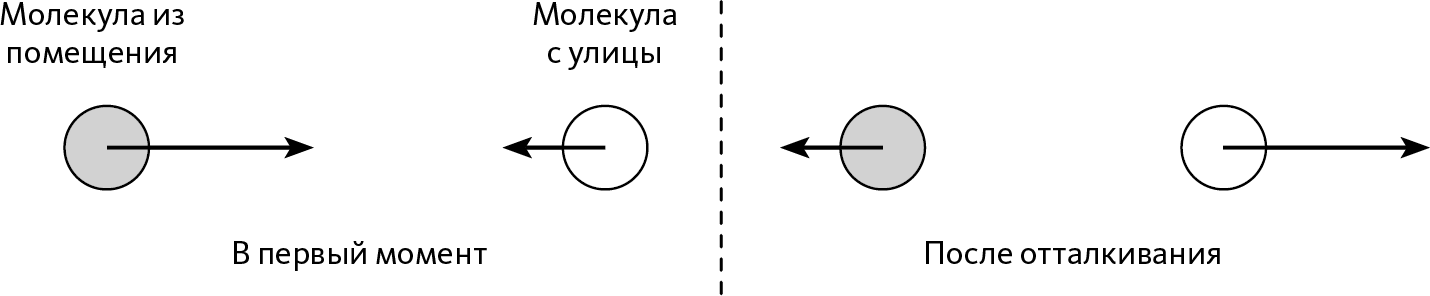
Рис. 8.5 – Столкновение двух молекул

Молекула из помещения осуществила положительную работу в отношении молекулы с улицы, повысив ее кинетическую энергию. Молекула с улицы осуществила отрицательную работу в отношении молекулы из помещения, уменьшив ее кинетическую энергию.

ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ

Мы описывали действие неконсервативной работы в виде: ΔE = A_NC, где ΔE – изменение энергии объекта.

Мы подразделяем неконсервативную работу на макроскопическую часть (A_NC^mac) и микроскопическую (теплота Q): A_NC = A_NC^mac + Q.

Мы подразделяем энергию на макроскопическую (механическая энергия E_m) и микроскопическую (внутренняя энергия U): E = E_m + U.

Теперь выражение принимает вид: ΔE_m + ΔU = A_NC^mac + Q.

(A_NC^mac представляет всю неконсервативную работу, кроме теплоты).

По ходу уточним, что теплота всегда является неконсервативной работой.

Выражение, записанное таким образом, называется первым началом термодинамики. Отметим, что данный закон не является результатом опыта, универсальность которого мы могли бы предположить, – это всего лишь следствие наших определений энергии и работы¹.