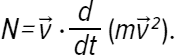8. Обмен энергией

В предыдущей главе говорилось о том, что мы можем терять или приобретать энергию с помощью обмена: как именно происходит этот обмен? Что необходимо предпринять, чтобы обрести энергию вновь? Для этого нам понадобится ввести новые понятия, связанные с передачей энергии: мощность и работа. Мы также уточним определение теплоты, которая является частным случаем работы и отличительным понятием температуры.

1. Работа и мощность

Что такое мощность?

Цель: повысить кинетическую энергию

«Воплощенной» формой энергии является энергия кинетическая, будь то макро- или микроскопическая. Именно ее мы в дальнейшем будем стараться увеличить. К потенциальной энергии мы вернемся позднее.

Как увеличить кинетическую энергию объекта? Необходимо, чтобы к нему была приложена какая-то сила, чтобы у него увеличилось ускорение. Но этого недостаточно, чтобы увеличить его скорость.

Возьмем Луну на ее круговой орбите: притяжение Земли удерживает Луну на ее орбите, но скорость ее остается постоянной. И действительно, сила перпендикулярна траектории Луны, то есть она придает ей нормальное ускорение, которое изгибает траекторию, но не увеличивает скорость (➙ рис. 8.1).

Теперь бросим яблоко. На этот раз гравитация позволит увеличить его скорость. Сила направлена по траектории яблока, то есть она оказывает тангенциальное ускорение, которое состоит в том, что увеличивает скорость.

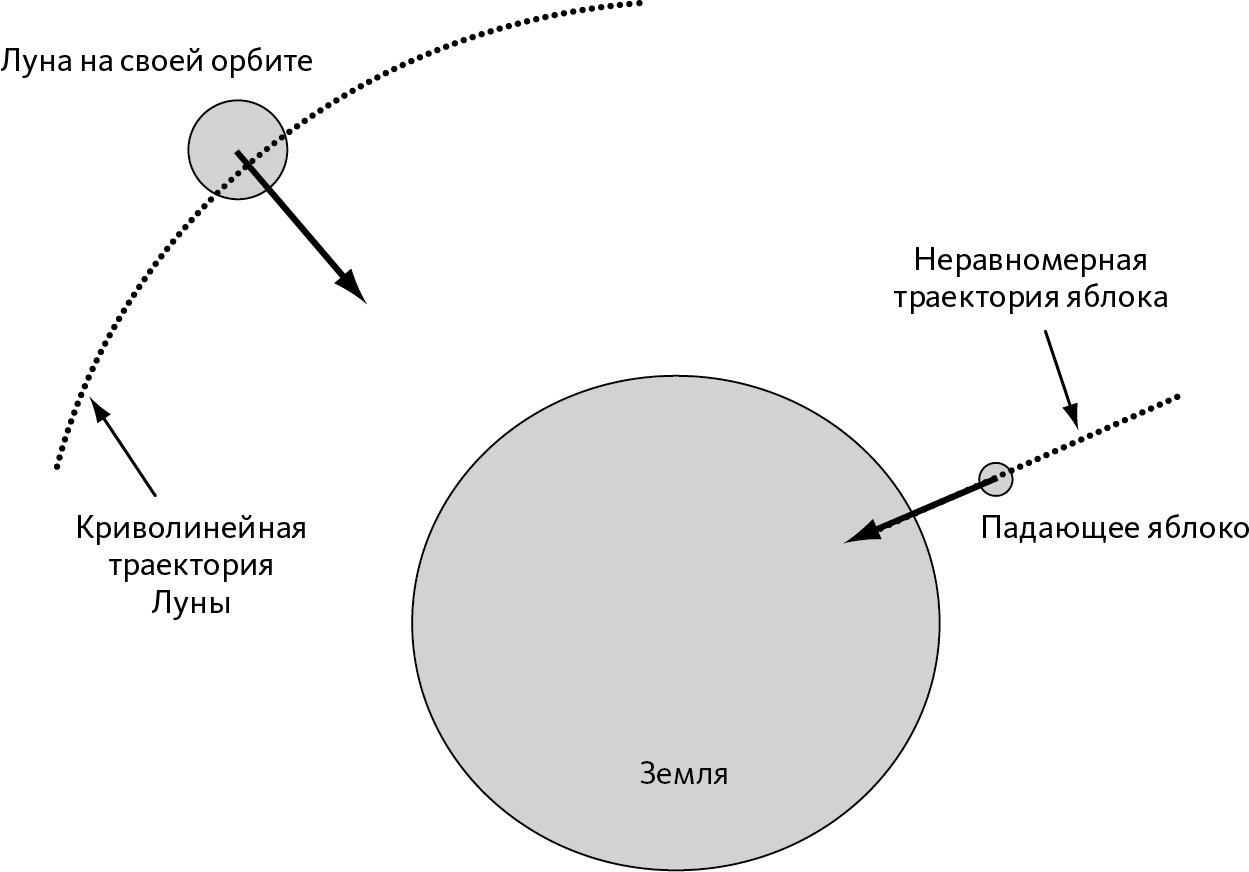
Рис. 8.1 – Сила, с которой Земля действует на Луну и на яблоко

Одним словом, чтобы кинетическая энергия объекта увеличилась, присутствия силы недостаточно: важно также ее направление. Посмотрим на рис. 8.2: в (а) сила увеличивает скорость объекта больше, чем в (b), потому что угол между вектором этой силы и траекторией объекта меньше. Мы скажем, что «мощность» этой силы больше.

Если угол 0 °, мощность максимальная, потому что сила целиком направлена на увеличение скорости объекта. Если угол 90°, мощность нулевая, потому что сила не увеличивает скорость. Если угол больше 90°, мы видим, что сила, напротив, тормозит объект (➙ рис. 8.2.с). В данном случае мы скажем, что мощность «отрицательная».

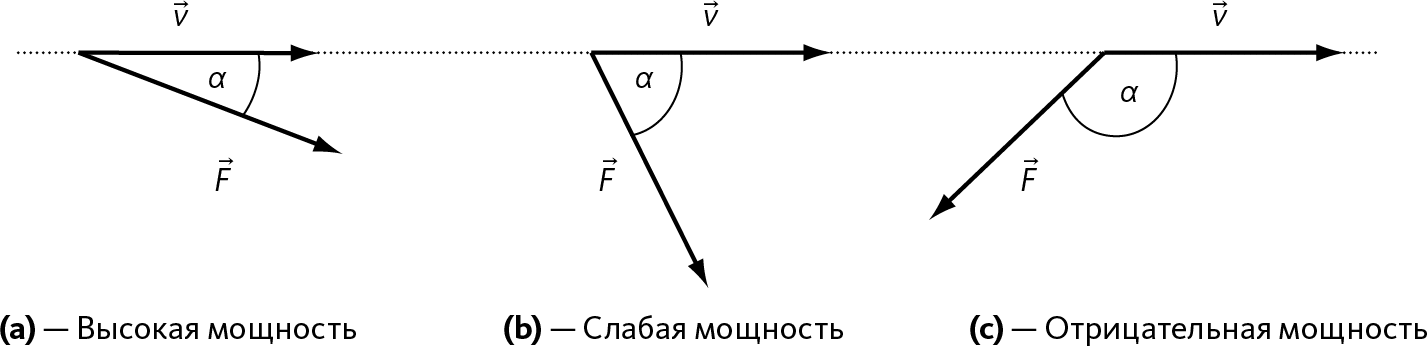
Рис. 8.2 – Мощность силы в зависимости от ее направленности

Если точнее, мощность будет пропорциональна cos α (если α = 0, cos α максимальный; если α = 90°, cos α = 0; если α > 90°, cos α – отрицательный).

Мощность представляет собой способность силы увеличить кинетическую энергию объекта ½mν² за единицу времени. Чтобы вывести формулу мощности, подведем итоги.

• Сила F^→; удовлетворяет выражению F^→; = ma^→; (где m – масса объекта, а a^→; – его ускорение), то есть она меняет mν^→; (где ν^→; – вектор скорости) за единицу времени.

• Произведение F cos α меняет mν (ν на этот раз величина скорости (➙ рис. 8.2).

• То есть произведение F ν cos α заставляет меняться ½mν²: речь идет о мощности.

Таким образом, формула мощности P выглядит P = F ν cos α.

Она пропорциональна приложенной силе F, косинусу угла α между этой силой и траекторией, а еще скорости ν объекта. Это означает, что чем быстрее двигается объект, тем большей мощности силу нужно приложить, чтобы увеличить его кинетическую энергию за определенный отрезок времени.

Запомним: мощность силы, приложенной к объекту, движущемуся со скоростью ν, определяется формулой P = F ν cos α. Она выражает изменение кинетической энергии, которую сила может вызвать за единицу времени. В этом случае общая мощность силы, с которой действует окружающая среда, равна изменению кинетической энергии объекта за одну секунду.

ВЫРАЖЕНИЕ МОЩНОСТИ: МАТЕМАТИЧЕСКОЕ ПОДТВЕРЖДЕНИЕ

Наша задача определить общую мощность, которая соответствует изменению кинетической энергии объекта за единицу времени: или .

Эта производная считается просто:

А поскольку , мы получаем N = ν^→; ⋅ F^→; (где F^→; – общая сила, которую оказывает окружающая среда).

Таким образом, мы находим F^→; ⋅ ν^→; = F ν cos α – определение мощности, которое используют физики. Речь идет об общей мощности, результате равнодействующей силы F^→;. Таким же способом мы можем определить мощность каждой силы в отдельности.

По ходу дела мы видим целесообразность коэффициента ½ в выражении кинетической энергии. Он исчезает, когда мы вычисляем производную от ν², что позволяет получить чрезвычайно простую формулу мощности: N = ν^→; ⋅ F^→;.

Некоторые обозначения мощности

Мощность выражается в ваттах. Мы уже немного знакомы с этой единицей благодаря электрическим приборам. Возьмем, к примеру, пылесос мощностью 1500 Вт (Вт – ватт): теперь мы знаем, что это означает. Такую электрическую мощность потребляет пылесос для выработки кинетической энергии за одну секунду. Эта энергия воплощается в очень разных процессах:

• сначала воздух приводится в движение, чтобы «засасывать» пыль, – это «полезная» кинетическая энергия пылесоса;

• коснувшись пылесоса, мы почувствуем, что он нагрелся, то есть он выработал микроскопическую кинетическую энергию (повышение температуры);

• наконец, пылесос производит много шума. Но шум производится молекулами воздуха, которые бьют по нашим барабанным перепонкам (к этому мы еще вернемся). То есть шум также связан с кинетической энергией.

Для наглядности приведем пример: мощность 1500 Вт необходима, чтобы сдвинуть с места автомобиль весом в 1000 кг, так чтобы его скорость за одну секунду изменилась с 0 км/ч до 6 км/ч. Для человека эта мощность весьма значительна, и без машин ему пришлось бы довольствоваться более низкими мощностями.

ДРУГИЕ ВЕЛИЧИНЫ МОЩНОСТИ

Мощность, вырабатываемая микроволновой печью и стиральной машиной, примерно одинакова (около 2000 Вт). Разница в том, что печь производит энергию на микроскопическом уровне (нагрев), а стиральная машина на макроскопическом (вращает барабан).

Сила тяжести также может выработать значительную мощность: тело в свободном падении приобретает скорость от 0 до 10 м/с за 1 секунду (таково ускорение свободного падения). То есть мощность, действующая на человека массой 60 кг, равна 3000 Вт.

Что касается мощности, которую может выработать человек, она весьма незначительна: велосипедист, разгоняющийся с 0 до 20 км/ч за 4 секунды, вырабатывает мощность всего лишь порядка 300 Вт.

В свою очередь, автомобиль при столкновении, которое за 100 миллисекунд заставляет его перейти от скорости 50 км/ч до 0 км/ч, испытывает отрицательную мощность около миллиона ватт. Такой удар очень болезнен.

Работать и только работать

Определение работы

Мощность силы соответствует изменению кинетической энергии, которое она может передать объекту за 1 секунду. Если эта мощность действует в течение четырех секунд, изменение энергии будет в четыре раза больше. Таким образом, если мы хотим узнать, на сколько изменится кинетическая энергия за отрезок времени t, нужно умножить мощность на количество времени t.

При постоянной мощности изменение кинетической энергии объекта в определенном промежутке времени равно произведению общей приложенной мощности N и количеству прошедшего времени t.

Это произведение Nt называется «работой» и обозначается буквой А (от нем. Arbeit – работа). Таким образом, работой силы называется прирост кинетической энергии, который она способна придать объекту за определенный отрезок времени.

Напомним, что мощность пропорциональна приложенной силе и скорости объекта. Работа также пропорциональна истекшему времени.

Как известно, при определенной скорости чем больше пройдет времени, тем большее расстояние пройдет объект. То есть работа попросту пропорциональна приложенной силе и расстоянию, пройденному объектом.

Пример

Проиллюстрируем определение работы на примере, чтобы сделать его понятнее.

Попробуйте сдвинуть шкаф. Если шкаф не движется, вы не оказываете на него никакой работы и никакой мощности (шкаф не приобрел кинетической энергии). То есть между вами и шкафом нет передачи энергии.

Но если вам удастся сдвинуть его, значит, вам удалось применить к нему работу: чем дальше вы его сдвинете, тем больше будет работа и тем больше энергии вы ему передадите.

Однако после того, как шкаф будет передвинут, он вновь останется неподвижным. Куда же делась кинетическая энергия, которую вы ему передали? Всему причиной трение поверхности: оно также проделало работу, но отрицательную, поскольку трение препятствовало движению. Таким образом:

• вы проделали положительную работу над шкафом («работа движущей силы»), благодаря чему ваша энергия передалась мебели: кинетическая энергия шкафа повысилась;

• трение поверхности осуществило отрицательную работу на шкаф («работа силы трения»), что передало энергию поверхности: это уменьшило кинетическую энергию шкафа.

В конечном итоге кинетическая энергия шкафа не увеличилась, а энергия, которую вы ему передали, перешла к полу (в микроскопической форме: шум и повышение температуры).

Итоги

В физике понятие работы является основополагающим, поскольку именно работа позволяет приобрести (или утратить) столь необходимую кинетическую энергию.

Если А означает общую приложенную работу, а E_k кинетическую энергию объекта, это записывают A = ΔE_k.

Символ Δ в физике означает изменение. Таким образом, это выражение означает, что изменение кинетической энергии объекта равно общей приложенной к нему работе (в том числе силы инерции, если она присутствует).

Работа представляет собой передачу энергии, и ее величина обозначается в джоулях, как и величина кинетической энергии. Благодаря электрическим компаниям нам известна и другая единица измерения: киловатт-час (кВт ⋅ ч): она представляет собой среднюю потребленную мощность (в киловаттах), помноженную на общее количество часов работы (на электросчетчике это количество часов может отображаться за многие годы, во время которых потреблялась электроэнергия).

Так, если счетчик, установленный год назад, показывает 5000 кВт ⋅ ч (что соответствует всей проделанной работе), это значит, что в среднем вы потребили 550 Вт мощности за час (в году 8760 часов). Держу пари, что общая кинетическая энергия, которую вы при этом приобрели, проявилась в основном на микроскопическом уровне: вы подогрели планету…