22‒симметричная красавица
Квадрат числа 222=484 запоминается из красоты симметрии. Внутри числа 22 есть число 11, поэтому при возведении этого числа в квадрат можно воспользоваться свойством умножения на 11.
222=22*22=2*11*2*11=44*11=484
Если к этому времени уже запомнили квадрат 21, то можно воспользоваться методом близкого квадрата.
212=441
222=441+21+22=484
Квадрат 484 является вторым числом-палиндромом.
23 – отличница
Число 23 детям называли «отличница в двадцать девятом царстве». Также его назвали «число-сумма» в двадцать девятом царстве».
Данные запоминалки придуманы потому, что
232=529
2+3=5
Запоминалка: «Ученики, которые учились на 2 и 3, вдруг стали учиться на 5 в 29-м царстве.
24 и 26 – первая пара близнецов
Это первая пара, в которой дети подмечают небольшую симметрию
242=576 и 262=676.
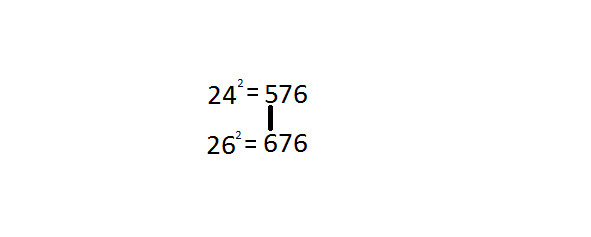
Квадраты чисел-близнецов 24 и 26
Если детьми не подмечено, что квадраты чисел оканчиваются на 76, то на это необходимо обратить внимание детей. Так как это позволит быстрее запомнить значение квадратов чисел без всяких расчётов. В то же время 76=100—24, а 26 и 76 просто созвучны.
В самих числах 24 и 26 тоже много особенностей:
1) числа 24 и 26 очень похожи друг на друга и различаются на одну цифру;
2) они расположены на числовой оси на одинаковом расстоянии от 25, одно слева, а другое справа;
3) 24+26=26+24=50, то есть они дополняют друг друга до 50.
Расчет значений этих чисел описан в главе Метод близкого квадрата. В данном случае близкий квадрат для удобного расчёта
252=625
242=625-25-24=576
262=625+25+26=676
Квадрат 676 является третьим и последним числом палиндромом.
27 – красавица смотрится в зеркало
272=729
Можно заметить, что 27 и 72 это зеркальные числа.
Можно придумать образ запоминалку:
«Число 27 смотрится в зеркало и видит 72 в 9-том королевстве».
28 – трудное число, расставь знаки
282=784
Для числа 28 и его квадрата нечего придумано не было. Рабочим названием для напоминания было «трудное число». Это название так и осталось как напоминание.
Потом для этому квадрата было придумано следующее:
28=7*4
Цифра 8 от числа 28 встаёт между множителями 7 и 4, получим 784. Ещё одно наблюдение, которое поможет сформировать нужные нейронные связи и поможет вспоминанию (2+8+2) *7=84. Таким образом в выражении 282=784 нужно просто переписать цифры с этого примера 282784 и расставить арифметические знаки по другому (2+8+2) *7=84.
29 – квадрат братьев, вежливый квадрат
292=841
Как заметила моя ученица Диана (в 2018 году Диана училась в третьем классе).
22=4
92=81
Старший квадрат 81 расступается и даёт место в серединке младшему квадрату 4, получается 841. Старший квадрат и будет вежливым.
Ещё этот квадрат легко считается от следующего квадрата
841=900-30-29.
31‒второе число-оборотень
312=961
Этот квадрат быстро и легко считается от предыдущего квадрата и в запоминании не нуждается.
312=900+30+31=961
Можно также заметить, что 132=169, можно также прочитать задом наоборот:
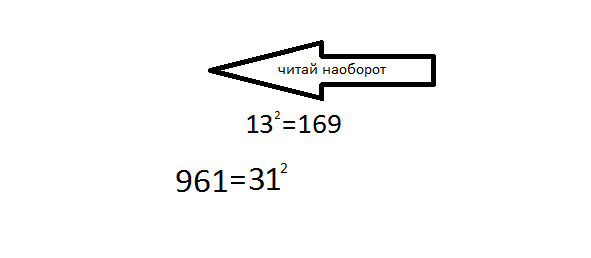
31-Второй квадрат-оборотень
Первый квадрат оборотень было число 441=212, поэтому 312=961 будет второй квадрат-оборотень.
32 – число кибернетики, выскочка единица
322=1024
Этот квадрат знают многие увлекающиеся программированием
322= (25) 2=210=1024
Можно также заметить такую связь между числами, которая поможет запомнить квадрат этого числа:
3+22=1+0+2+4
Таким образом цифра 3, разбивается на три цифры 0, 1, 2. И единица (выскочка) хочет стать первой в ряде последовательных цифр из двоичного кода 0, 1, 2, 4.
0=00
1=20
2=21
4=22
33, 66, 99‒три брата, квадраты 33 и 99 числа-оборотни
Числа 33, 66 и 99 вместе со своими квадратами тесно связаны с числом 99.
А связаны они с друг другом математическими соотношениями
33+66=99
332=1089
662=4356
992=9801
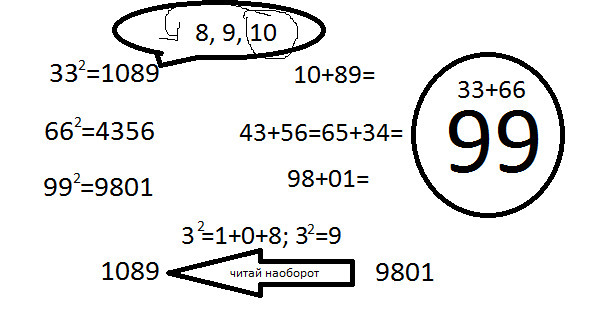
Квадраты 33, 66 и 99
Квадраты 1089 и 9801 читаются справа налево и слева направо. Такие квадраты (1089 и 9801) называем оборотни, но в данном случае сами числа (33 и 99) не оборотни.
В квадрате 4356, есть четыре последовательных цифры: 3, 4, 5 и 6.
Сами квадраты связаны с 99, через такие соотношения
10+89=43+56=65+34 =98+01=99
Для запоминания первого квадрата можно подметить
32=1+0+8, 32=9.
Также можно заметить, что, если взять три числа 8, 9, 10 и переставить число 10 в числе 8910 на первое место, то будет 1089.
34 дружит с барабанными палочками
Квадрат числа 34 поможет запомнить следующее наблюдение
342=1156
3+1+1=5
4+1+1=6
34+2*11=56

Квадрат 34
Осталось добавить, что в мнемотехнике 11 называют «барабанными палочками», а 34 связано со знаменитым танком Т-34.
36 – акробат
362=1296
Этот квадрат заучить просто по созвучию и как стихи:
«Тридцать шесть – тысяча двести девяносто шесть».
«Тридцать шесть – двенадцать и девяносто шесть».
Конечно можно поискать какие-либо математические связи
3=1+2. А 62 пишем два раза цифру 6, сначала перевёрнуто 9, а потом правильно.
(6+2) *12=8*12=96.

