Мнемотехника для запоминания квадратов чисел
Поскольку данная методика применялась в группах детей от третьего класса, то придумывались запоминалки и образы (узелки на память) для детей такого возраста. Некоторые из узелков на память придумывались сами детьми. В данном разделе я их приведу для облегчения внедрения методики.
На легкие числа (те, которые легко считаются в уме), никакие запоминалки не придумывались, так как их можно быстро посчитать в уме. Это числа оканчивающиеся на 0 и 5, а также из промежутка от 11 до 19.
Метод повторения через промежутки
Запоминаем квадраты находящиеся в одном десятке. Например,
1) квадраты чисел от 11 до 19
2) квадраты чисел от 21 до 29
3) квадраты чисел от 31 до 39
Знания квадратов от 11 до 39 достаточно для подсчета всех других квадратов методом кода числа. Но, если необходимо вспоминание менее секунды, то необходимо тренировать и другие квадраты.
Запоминание и вспоминание делаем в определенные промежутки, в зависимости от того, как прочно и как надолго собираетесь запомнить и будете ли применять в повседневной жизни (например вы математик или фокусник в математическом жанре).
1) первая неделя – вспоминаем и тренируем каждый день;
2) вторая неделя – вспоминаем и тренируем каждые 2—3 дня;
3) третья неделя – вспоминаем и тренируем в начале и конце недели;
4) четвертая неделя – вспоминаем и тренируем в середине недели;
5) 2 месяц – тренируем и вспоминаем 1 раз в 2 недели;
6) 3 месяц – тренируем и вспоминаем 1 раз в месяц;
7) 4—9 месяц (полгода) тренируем и вспоминаем 1 раз в три месяца
8) 1 год – тренируем и вспоминаем 1 раз в в полгода.
Симметрия квадратов
В таблице даже детьми младшего возраста наблюдается симметрия значений квадратов. Это уже не такая симметрия, которая описана в моей книге «Таблица умножения за 3 дня». Здесь уже наблюдается симметрия окончаний квадратов. Первую такую симметрию дети подмечают изучая квадраты чисел 24 и 26.
242=576 и 262=676
Далее дети подмечают другие такие близкие пары, например,
742=5476 и 762=5776
11—19
В принципе для этой группы не используются никакие приемы, кроме быстрого умножения. Группа этих чисел подробна рассмотрена в главе ФОРМУЛА КВАДРАТОВ ЧИСЕЛ ОТ 11 ДО 19.
Но все же некоторые подмеченные особенности я покажу. Вполне возможно, это поможет Вам быстрее запомнить данную группу.
Первая группа вообще не вызывает затруднений даже у школьников младших классов.
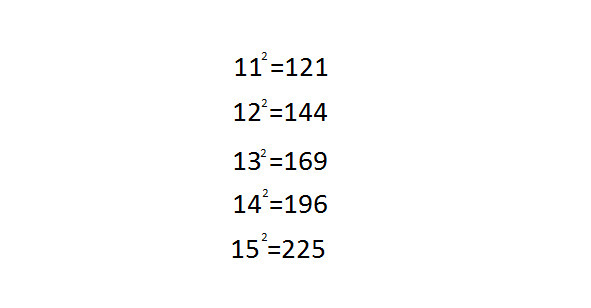
Квадраты чисел 11—15
112 можно умножать пользуясь правилом умножения на 11.
Для того, чтобы умножить на 11 двузначное число, необходимо это двузначное число раздвинуть на один разряд, а вместо этого разряда поместить сумму левого и правого чисел.
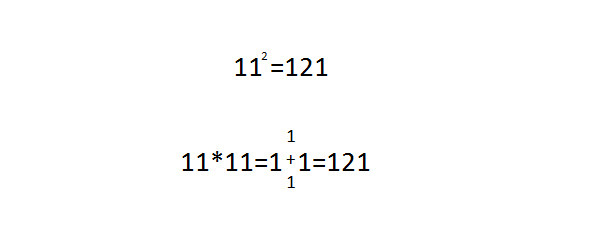
Квадрат 11
Квадрат 112=121 является первым трехзначным числом палиндромом.
122 также почему-то не вызывает трудностей, может быть из-за близкой ассоциации 22=4.
132 и 142 квадраты-зеркала и запоминаются совместно. Число 169, если перевернуть (отразить сверху вниз относительно горизонтали) будет 196 (если отразить по горизонтали, то цифра 1 отразится в 1, цифра 6 в 9, а цифра 9 в 6).
152 вполне можно быстро подсчитать по разным формулам (смотри главу ФОРМУЛА КВАДРАТОВ ДЛЯ ЧИСЕЛ, ОКАНЧИВАЮЩИХСЯ НА 5) и запоминается тоже хорошо.
А вот четыре других квадрата вызывают небольшую заминку при вспоминании, но тоже вполне хорошо запоминаются.
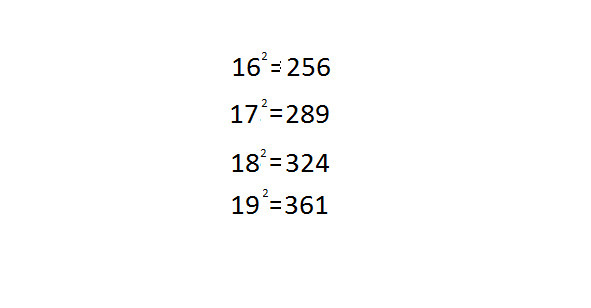
Квадраты чисел 16—19
162=256 вполне запоминается как рифма «шестью ю шесть тридцать шесть». Здесь рифма немного изменяется «шестнадцатью ю шестнадцать двести пятьдесят шесть».
172=289 объявите конкурс среди детей кто быстрее запомнит.
Можно заметить, что число 56789 своими цифрами участвует в образовании квадратов 256 и 172=289.
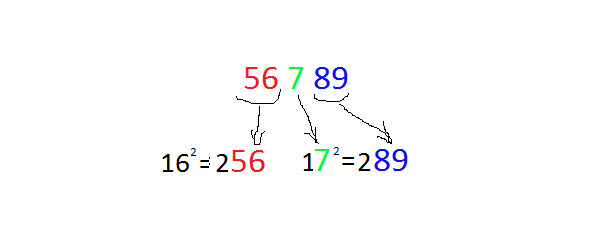
Квадраты 16 и 17
182 быстро считается по формуле: 182=260+64=324.
Для этого квадрата, если расположить цифры 182 и 324, то можно увидеть такую взаимосвязь.
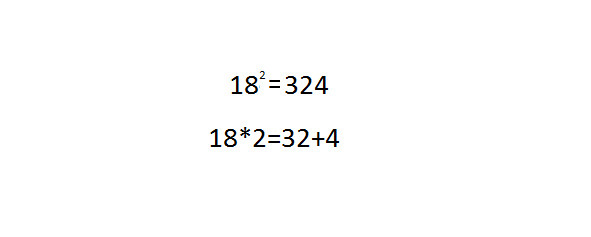
Квадрат 18
192 можно считать методом близкого квадрата от 202=400.
192=400-20-19=361
20, 30, 40, 50, 60, 70, 80, 90
Квадраты этих чисел очень легко считаются и остановились на них просто для законченности логики книги.
15, 25, 35, 45, 55, 65, 75, 85, 95
Квадрат таких чисел легко считаются методом квадратов, заканчивающихся на 5. Данная глава написана просто для порядка.
152=225
252=625
352=1225
452=2025
552=3025
652=4225
752=5625
852=7225
952=9025
21‒число и квадрат оборотни
Так это число назвал, из-за подмеченной зависимости от числа и квадрата 122=144. Если 12 прочитать задом наперёд, то получим 21. И если квадрат 122 прочитаем задом наперёд, то из 144, получим 441.
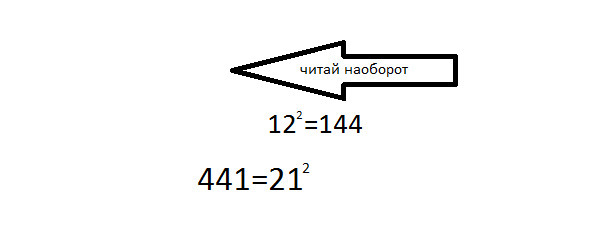
Квадрат 21 (число и квадрат оборотни)
Можно 212 также быстро считать по методу близкого квадрата от 202=400.
212=400+20+21=441.

