Метод основания
Метод применяется как частный случай умножения двух чисел, которые близки к какому-либо числу. Это близкое число называется основанием. Сам метод возведения таким способом будем называть методом основания. В качестве основания выбираются числа заканчивающиеся на 0. Если число заканчивается на 0, то на такое число легко умножать, так как здесь умножать нужно на однозначное число и потом приписать к результату 0 (умножить на 10).
Число которое заканчивается на 0 часто называют основанием. А сам метод называется метод по основанию или короче метод основания.
Правило:
Чтобы умножить два числа нужно увеличить и убавить оба числа на одно и тоже число (так чтобы одно из них стало основанием) и прибавить квадрат числа на которое изменяли оба числа.
Примеры:
1) 422
422= (42+2) * (42—2) +22=44*40+4=1764
2) 832= (83+3) * (83—3) +32=86*80+9=6889
3) Данное правило можно использовать для умножения не только квадратов
76*77= (80—4) * (80—3) =80*80—4*80—3*80+ (-4) * (-3) =80* (80-3-4) +12=80*73+12=5840+12=5852
Доказательство:
(10X+Y) * (10X+Z) =10X*10X+10XY+10XZ+Y*Z=10X * (10X+Y+Z) +Y*Z
Таким образом получили что основание для данного умножения будет 10х. А другое число (10X+Y+Z) получается, если к первому числу (10X+Y) добавить единицы Z второго числа, или наоборот ко второму числу 10X+Z добавить единицы Y первого числа. К получившемуся произведению добавить произведение единиц Y*Zпервого и второго чисел.
Аналогично
(10X-Y) * (10X-Z) =10X*10X-10XY-10XZ+Y*Z=10X * (10X+Y+Z) +Y*Z
(10X-Y) * (10X+Z) =10X*10X-10XY+10XZ-Y*Z=10X * (10X-Y+Z) -Y*Z
Данный метод применен в главе ФОРМУЛА КВАДРАТОВ ЧИСЕЛ ОТ 11 ДО 19 при Х=1.
Метод кода числа для квадратов
Этот авторский метод я использую для подсчёта и быстрого вспоминания квадрата. Несмотря на то, что теперь просто использую код для припоминания квадрата, метод позволяет со 100% точностью вычислить квадрат любого числа от 01 до 99. При большом навыке использования этот метод сначала позволяет быстро вычислить квадрат, а потом вспоминать его по первым двум цифрам. Я различаю несколько кодов числа для вспоминания квадрата:
1) вспомогательный код;
2) истинный код (в дальнейшем именно его буду называть просто код или код числа). Именно вычислить истинный код и является целью данного метода.
3) двойной код;
4) задний код.
У любого числа всегда есть истинный код. На этом коде и основан метод. Все другие коды не всегда имеются у числа и просто используются для быстро подсчёта либо истинного кода, либо самого квадрата. Например, двойной код есть только у чисел: 51, 68 и 84. Задний код только у чисел 68, 76. Вспомогательный код есть у всех чисел (86—99) лестницы.
Подробнее станет понятно, что автор имеет ввиду на примерах в разделе Мнемотехника.
Некоторые особенности возведения в квадрат
Если возвести все числа от 01 до 99 (можно взять и другие числа более 99, но цикл повторится) можно заметить, что квадраты чисел имеют вполне дискретный ряд двузначных окончаний.
Таких окончаний всего 22. Выпишем данный в порядке возрастания:
00, 01, 04, 09, 16, 21, 24, 25, 29, 36, 41, 44, 49, 56, 61, 64, 69, 76, 81, 84, 89, 96
Других окончаний любого квадрата быть не может. В конце главы докажем данное утверждение.
Также можно заметить, что квадраты чисел получающихся путём
Х, 50‒Х, 50+Х, 100‒Х, 100+Х, 150‒Х, 150+Х, 200‒Х, 200+Х, или n*50±Х, где n∈Z (0, ±1, ±2, ±3,…)
всегда заканчиваются на одно и тоже двузначное окончание. Это также можно доказать.
Примеры
1) Квадраты чисел 24, 26, 74, 76, 124, 126 и т. д. заканчиваются на 76
2) 3, 47, 53, 97, 103, 147, 153 и т. д. всегда заканчиваются на 09
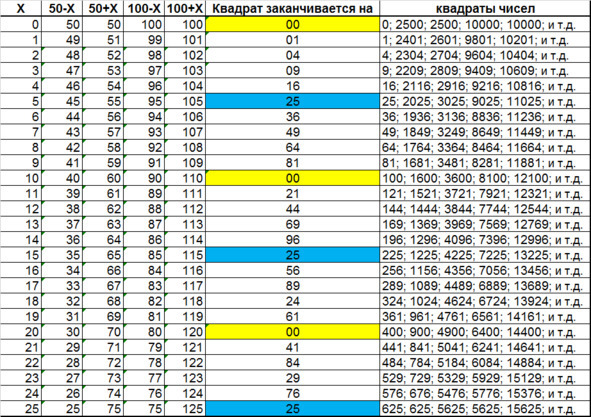
Зависимость окончания квадрата от числа
Из вышесказанного можно сделать вывод, что необязательно возводить большие числа любого ряда получающего таким образом, достаточно возвести первое или второе число.
Иногда быстрее будет не возвращаться к первому числу, а взять последние две цифры от второго числа. Данное обстоятельство станет понятнее при рассмотрении примеров в других главах книги. Пока не будет на этом останавливаться.
Остальная часть главы написана для любознательных, и читатель вполне может её пропустить.
Окончания квадратов также подчиняются внутренним правилам и для удобства их можно даже упорядочить в таблице и назвать.
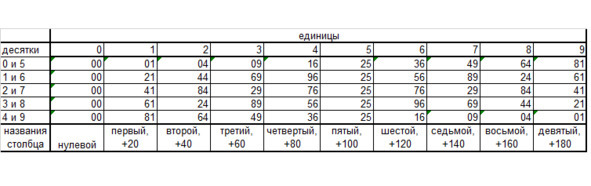
Окончания квадратов в таблице
Поясним данную таблицу.
Предположим хотим знать на какие две цифры, заканчивается квадрат 62. Смотрим по таблице: видим 6 десятков и 2 единицы. Значит квадрат числа закончится на 44. Действительно 622=3844. Также на 44 закончится и 12, 38=50—12, 62=50+12, 88=100—12:
122=0144
382=1444
622=3844
882=7744
Сами ряды также названы (название совпадает с количеством единиц) для лёгкого запоминания. И ряды легко получаются из значения первого путём добавления прибавления соответствующего числа (указано в названии внизу). Если число в результате суммирования становится трехзначным, то мы отбрасываем значения сотен и оставляем только две значащие цифры начиная справа (десятки и единицы).
Пример
1) Третий ряд начинается с 09, далее 09+60=69, 69+60=129 (отбрасываем сотни, остается 29), далее 29+60=89, потом 89+60=149 (оставляем 49).
2) Нулевой и пятый ряд получаются путём прибавления 00 или 100, но для пятого выбрано 100. Число 100 выбрано, чтобы вы увидели прогрессию в данной таблице.
Само число, которое нужно прибавлять для получения следующего окончания данного ряда вполне подчиняется формуле: количество единиц умножить на 20. Например шестой ряд содержит 6 единиц, значит нужно прибавлять 6*20=120.
Конечно таким образом вычислять окончания квадратов нам не придётся, таблица приведена в качестве небольшого исследования в данном вопросе.
Все окончания можно разделить на пары, которые являются дополнением друг друга. Можно выделить не только пары, но и ряды.
1
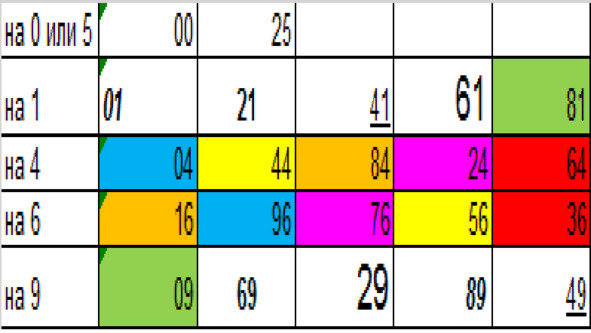
Окончания квадратов -пары
Как видно из рисунка, видно что можно условно все окончания квадратов выделить в различные ряды:
1) оканчиваются на 0 или 5;
2) оканчиваются на 1;
3) оканчиваются на 4;
4) оканчиваются на 6;
5) оканчиваются на 9.
Внутри ряда всех окончаний можно условно поделить на пары, которые в сумме дают 100. Таких пар шесть и они выделены цветом:
(04, 96), (09, 81), (16, 84), (24, 76), (36, 64), (44, 56)
Другие пары в сумме дают 90. Они по разному выделены различными шрифтами. Таких пар четыре:
(01, 89), (21, 69), (29, 61), (41, 49)
И последняя особая пара (00, 25). И то и другое окончание не изменяется в своём ряду.
Доказательство.
Утверждение 1. Квадраты чисел Х, 50-Х, 50+Х, 100-Х, 100+Х, …, чисел вида n*50±Х где Х, n∈Z (0, ±1, ±2, ±3,…) заканчиваются на одинаковое двузначное число.
Действительно, (n*50±Х) 2=2500*n2±100nХ+Х2=100* (25n2+nХ) +Х2
Выражение 100* (25n2+nХ) влияет только на значения цифр сотен в квадрате числа. Десятки и единицы всех чисел вида (n*50±Х) 2 и Х2 будут одинаковы, различие будет начинаться только с разряда сотен.
Утверждение 2. Окончаний квадратов всего 22: 00, 01, 04, 09, 16, 21, 24, 25, 29, 36, 41, 44, 49, 56, 61, 64, 69, 76, 81, 84, 89, 96.
Для доказательства Утверждения 2 достаточно выписать все квадраты от 1 до 25. Выше это сделано в таблице. Все другие окончания согласно Утверждения 1 будут повторяться.

