Формула квадратов чисел от 25 до 50
Многие вычислители (ментальные счётчики, фокусники-математики) используют следующую формулу для вычисления чисел из отрезка [25;50].
ХУ2= (ХУ-25) *100+ (50-ХУ) 2

Формула для вычислений квадратов чисел от 25 до 50 включительно
Для использования формулы потребуется хорошее знание квадратов чисел до 25.
Формула квадратов чисел от 50 до 100
Вторая формула применяемая вычислителями, используется для чисел от 50 до 100 включительно:
ХУ2= (ХУ-50) *200+ (100-ХУ) 2

Формула для вычисления квадратов чисел от 50 до 100 включительно
Использование формулы потребует знания квадратов чисел до 50.
Например, для подсчёта квадрата 67, необходимо знание квадрата числа 33=100—67.
Формулы сокращенного умножения
Для вычисления квадратов чисел используют всего две формулы из всех формул сокращенного умножения:
(a+b) 2=a2+2*a*b+b2;
(a‒b) 2=a2—2*a*b+b2.
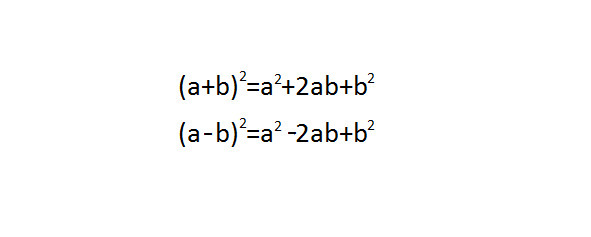
Формулы сокращённого умножения
Формулы сокращенного умножения в школьном курсе используются для подсчета квадратов для чисел близких к круглым.
Например, необходимо подсчитать квадрат числа 41. Тогда по формуле сокращенного умножения легко преобразовать:
412= (40+1) 2=402+2*40*1+12=1600+80+1=1681
392= (40—1) 2=402—2*40*1+12=1600—80+1=1521
Квадрат числа, которое на единицу отстаёт (возрастает) от легковычисляемого квадрата приведены выше. Вычислим квадраты чисел, которые отстают (возрастают) на 2 единицы.
422= (40+2) 2=402+2*40*2+12=1600+160+22=1764
382= (40—2) 2=402—2*40*2+22=1600—160+4=1444
Далее, если число отстаёт (возрастает) на 3 единицы сложность вычислений немного увеличивается:
432= (40+3) 2=402+2*40*3+32=1600+240+9=1849
372= (40—3) 2=402—2*40*3+32=1600—240+9=1369
Если рассматривать числа, которые отстают (возрастают) на 4 единицы, то сложность вычислений по сравнению с другими методами или даже другим выбором «круглого» квадрата очень большая:
442= (40+4) 2=402+2*40*4+42=1600+320+16=1936
362= (40—4) 2=402—2*40*4+42=1600—320+16=1296
Сравните с другими методами:
а) формула квадратов для чисел от 25 до 50
442= (44—25) *100+ (50—44) 2=1900+36=1936
362= (36—25) *100+ (50—36) 2=1100+196=1296;
б) формула сокращенного умножения с выбором другого квадрата
442= (45—1) 2=452—2*45*1+12=2025—90+1=1936
362= (35+1) 2=352+2*35*1+12=1225+70+1=1296
Таким образом можно сделать вывод что формулы сокращенного умножения удобно использовать, если число близко к круглому числу (оканчивающимся на 0 или на 5) на одну единицу. В остальных случаях (числа заканчиваются на цифры 3 и 7) лучше использовать другие формулы для вычислений.
Метод близкого квадрата
Метод близкого квадрата использует формулы сокращенного умножения в другом виде. Для использования метода необходимо знать квадрат числа соседнего с искомым числом. Соседнее число, это число на единицу больше или меньше числа, для которого ищем квадрат. Если непонятно сейчас, то на примерах станет понятно.
Правило:
Чтобы найти квадрат следующего (предыдущего) числа, необходимо к квадрату предыдущего числа прибавить (отнять) число, которое у которого знали квадрат и само число, у которого ищем квадрат.
Метод близкого квадрата неудобно применять для чисел, оканчивающихся на цифры 3 и 7, так обычно немногие помнят или могут быстро подсчитать ближайшие квадраты.
Пример 1.
Необходимо найти 312, зная квадрат числа 30: 302=900
Здесь 31 следующее число после 30. 900 квадрат числа 30, который известен или его легко подсчитать очень быстро.
312=900+30+31=961
Пример 2.
Необходимо найти 292, зная квадрат числа 30: 302=900
Здесь 29 предыдущее число от 30, квадрат, которого известен. Так как нам нужно квадрат предыдущего, то мы отнимаем числа:
292=900-30-29=841
Доказательство.
Доказательство сразу получается, если формулы сокращенного умножения немного переформулировать, учитывая, что b=1
(a+1) 2=a2+2*a*1+12= a2+2*a+1=a2+a+ (a+1)
(a‒1) 2=a2—2*a*1+12= a2—2*a+1=a2‒a‒ (a‒1)
Получим, что a+1 и а-1, это число, которое нужно возвести в квадрат. Число а это число квадрат, которого известен а2.
Формула для квадратов чисел от 91 до 99
На своих уроках я проделываю такой опыт. Выписываем все квадраты от 91 до 99. Квадраты можно посчитать различными способами (смотри соответствующие главы – Метод близкого квадрата, Формулы сокращенного умножения и др.):
912=8281
922=8464
932=8649
942=8836
952=9025
962=9216
972=9409
982=9604
992=9801
Далее даю задание ученикам: Как найти квадрат числа не прибегая к полному вычислению каким-либо способом. По-моему опыту с таким заданием справляются ученики 7—8 класса. Ученики подмечают, что ряд чисел, составленный из разрядов тысяч и сотен увеличивается на 2: 82, 84, 86, 88, 90, 92, 94, 96, 98. В тоже время ряд чисел, составленный из разрядов десятков и единиц это полные квадраты убывающего ряда чисел (9, 8, 7, 6, 5, 4, 3, 2, 1): 81, 64, 49, 36, 25, 16, 09, 04, 01.
Ещё немного подумав и отвечая на направляющие вопросы наконец самостоятельно находят способ как получать квадраты числа зная само число от 91 до 99. Совершив это маленькое открытие, они очень довольны собой и математика немного становится любимым предметом. А для кого-то эта красота мира чисел оказывает решающее значение и определяет выбор жизненного пути.
Для тех, кто не догадался о способах получения квадрата по числу от 91 до 99 приведу две формулы:
9Х2= (100‒ (10‒Х) *2) *100+ (10-Х) 2;
9Х2= (80+Х*2) *100+ (10-Х) 2
На самом деле формулы действительны для чисел от 90 до 99, но вычислять 90 таким способом слишком неоптимально. Поэтому число 90 исключено из этого промежутка. Вторая формула из представленных более предпочтительна.

