День второй

Квадраты

Наша неизученная таблица умножения содержит 49 примеров (рисунок 16). Второй день обучения начнем с главной диагонали – примеры умножения одинаковых чисел (синие числа в жёлтом квадратике). Такие результаты выделены в таблице квадратиками жёлтого цвета.

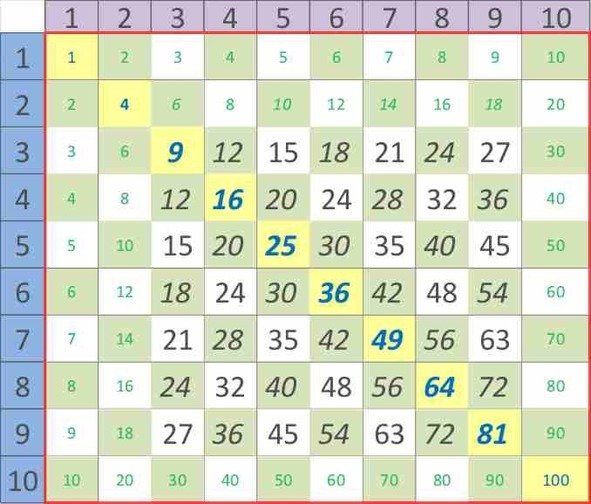
Рисунок 17. Примеры умножения на главной диагонали.

В старших классах, когда число умножается само на себя, говорят, что надо найти квадрат числа.

Выпишем все примеры умножения чисел с результатами на главной диагонали (квадраты).

Рисунок 18. Примеры с главной диагонали (неизученные).

Дальше найдите и дайте прослушать школьнику несколько раз песенку «Дважды два четыре» – слова Пляцковского М., музыка- Шаинского В. Если ребенок будет подпевать, то выучите несколько примеров на умножение.

В песне следующие примеры: 2*2=4, 3*3=9, 5*5=25, 6*8=48, 6*6=36.

Чтобы запомнить остальные примеры умножения одинаковых чисел, предлагаю воспользоваться отрывками из стихотворений М. Казариной и А. Усачёва.

Рисунок 19. Стихотворения для 4*4=16

Для примера 7*7=49.

Рисунок 20. Стихотворение для примера 7*7=49

Многие дети играли в шашки или шахматы и прекрасно знают, что 8 строк и 8 столбцов шахматной доски образуют 64 клетки шахматной доски -32 белых и 32 черных.

Рисунок 21. Шахматная доска, 8*8=64

Тем не менее привожу отрывки и для этого примера 8*8=64:

Рисунок 22. Стихотворение для примера 8*8=64

Остался последний пример этой главы 9*9=81. Разумеется, мы еще встретимся с этим примером, когда будем рассматривать умножение на 9. Умножение на 9 считается одним из легких – оно по легкости приближается к примерам умножения из первого раздела (умножение на 1, на 2, на 10). Запоминать этот пример необязательно, я его приведу для того, чтобы просто закончить данную главу:

Рисунок 23. Стихотворения для примера 9*9=81

После изучения этого раздела, в составе которого всего одна глава, нам осталось выучить 42 примера умножения.

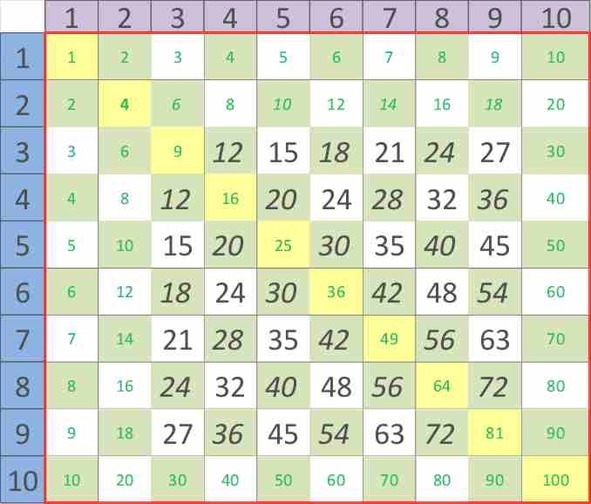
Рисунок 24. Таблица Пифагора, после второго дня методики

День третий

Симметрия таблицы Пифагора

Приступим к изучению оставшихся примеров умножения – их осталось 42 примера. Для того, чтобы облегчить себе задачу, рассмотрим симметрию таблицы Пифагора (математики говорят о симметричности умножения). О симметрии уже говорилось в разделе Введения, когда рассматривали пример 5*6=6*5=30. Если еще не увидели симметрию таблицы Пифагора относительно главной диагонали (примеры умножения числа самого на себя), то раскрашу таблицу таким образом:

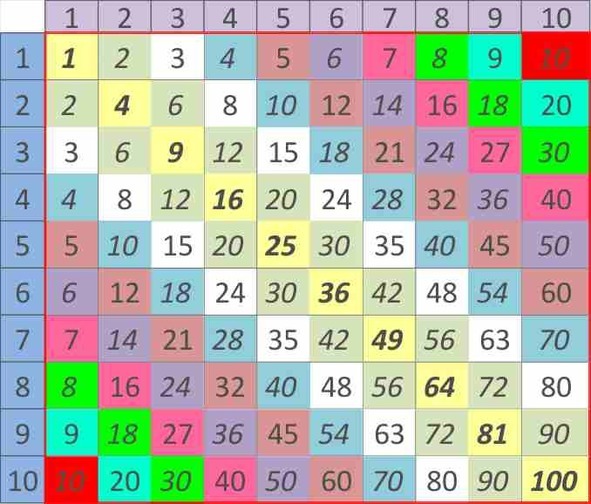
Рисунок 25. Симметрия таблицы Пифагора

Каждому квадратику таблицы, кроме жёлтых квадратиков главной диагонали, можно поставить в соответствие зеркального брата-близнеца.

Рисунок 26. Правило симметрии умножения

Из-за этого свойства симметрии вместо 42 примеров будем изучать ровно половину – 21 пример:

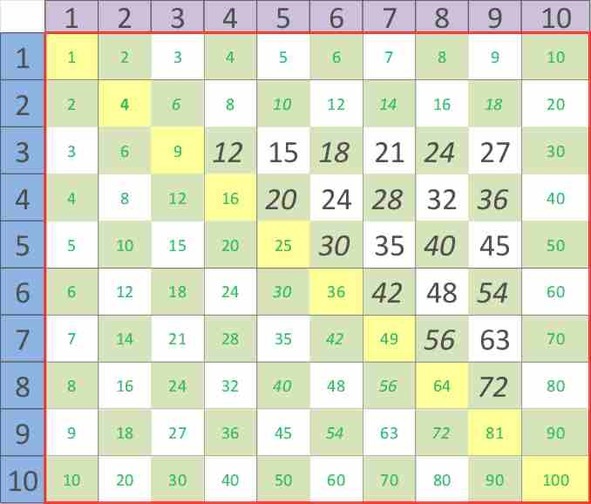
Рисунок 27. Таблица Пифагора для изучения (после применения правила симметрии)

Умножение на 9

Начнем изучение 21 примера с умножения на 9 – самых многочисленных из оставшихся примеров.

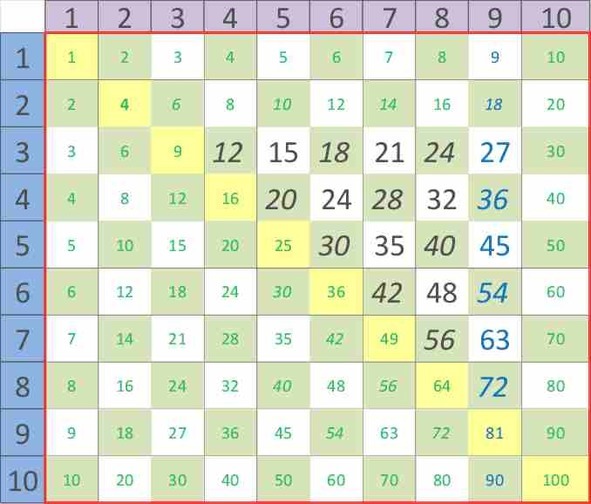
Рисунок 28. Умножение на 9.

Способов умножения на 9 несколько. Вот основные из них:

Рисунок 29. Способы умножения на 9

Умножение на 9- умножение на пальцах

Опишем способ умножения на 9 с помощью пальцев.

Для этого пронумеруем пальцы рук слева направо.

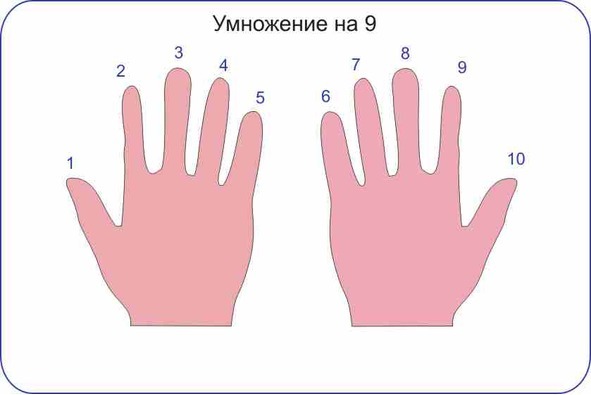
Рисунок 30. Нумерация пальцев рук

Для того, чтобы умножить число на 9, надо загнуть палец с этим номером. Количество пальцев до загнутого пальца (отмечу палец зеленой полоской) это десятки произведения, количество пальцев после загнутого пальца это единицы произведения.

Для примера умножим 3*9=?

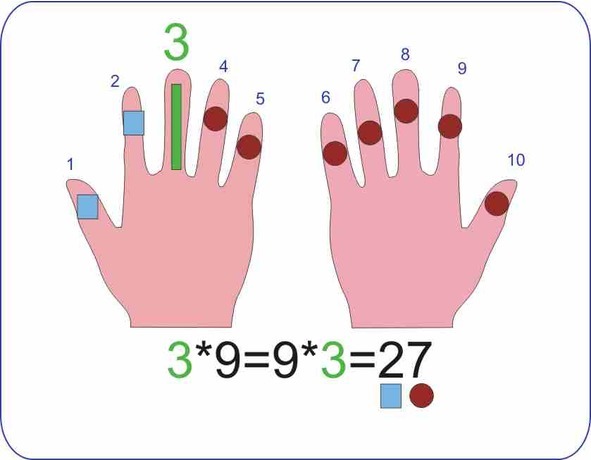
Рисунок 31. Как умножить 3*9 на пальцах рук

Второй пример, 9*9=?

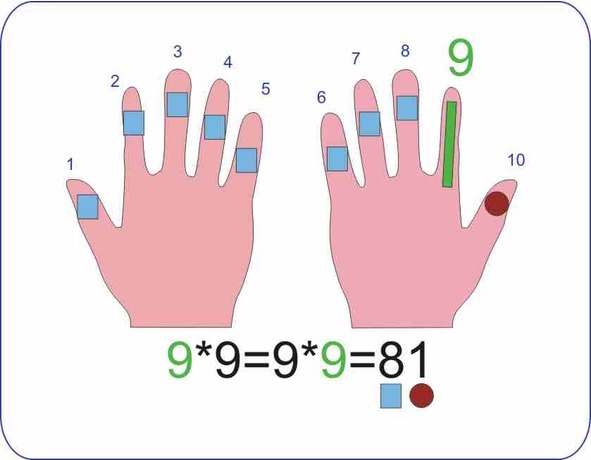
Рисунок 32. Как умножить 9*9 на пальцах рук

Умножение на 9. 9=10—1

Этот способ универсален и подходит для любых чисел.

Для того, чтобы умножить число на 9, сначала умножим его на 10 (припишем к числу 0 справа) и затем отнимем от результата умножения на 10 само число.

8*9=8 (10—1) =80—8=72

6*9=60—6=54

Свойство девятки (способ умножения на 9)

Данный способ распространяется на все числа, но мы рассмотрим его только для чисел от 1 до 10. Способ основан на признаке делимости на 9.

Рисунок 33. Способ умножения 9 (третий способ)

Покажем это на примерах, чтобы стало понятнее.

Итак, умножим 3*9=???

1. Отнимаем от 3 единицу 3—1=2 (получили число десятков)

2. Дописываем справа от десятков, число единиц кратное 9 (для этого от 9 отнимем полученное число десятков 2 – будет 9—2=7) Итак, 3*9=27

Еще пример, 6*9=???

1. 6—1=5 -число десятков

2. 9—5=4- число единиц Итак, 54=6*9=9*6

Последний пример 9*9=???

1.9—1=8

2. 9—8=1 Итак, 81=9*9 (как видим такой пример можно не учить, если знать правило умножения на 9).

После этой главы нам осталось 15 примеров умножения.

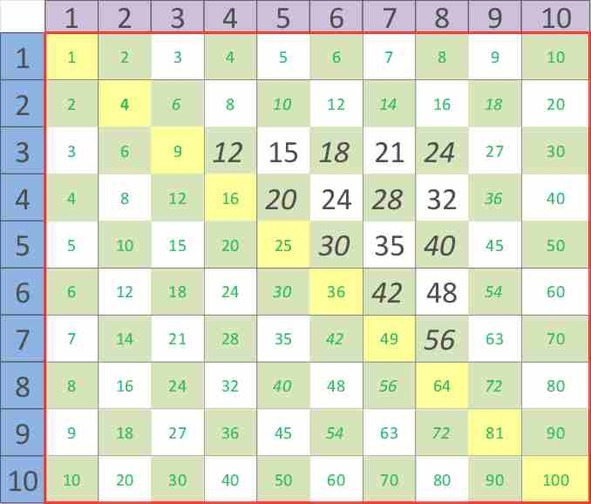
Рисунок 34. Таблица Пифагора -15 неизученных примеров