Что такое волна?

Какая-нибудь сплетня, начавшаяся в Вашингтоне, очень быстро доходит до Нью-Йорка, несмотря на то что ни одно лицо, принимавшее участие в ее распространении, не передвигалось между этими двумя городами. Имеются два совершенно различных способа передачи или движения слухов из Вашингтона в Нью-Йорк и движения лиц, передающих слух.

Порыв ветра, проносясь над хлебным полем, создает волну, которая распространяется по всему полю. И здесь опять мы должны различать между движением волны и движением отдельных растений, которые совершают лишь малые колебания. Все мы видели волны, которые распространяются все более и более широкими кругами, когда в воду брошен камень. Движение волны сильно отличается от движения частиц воды. Частицы движутся лишь вверх и вниз. Наблюдаемое движение волны – это перемещение состояния вещества, а не самого вещества. Пробка, плавающая на волне, ясно показывает это, ибо она движется вверх и вниз, подражая действительному движению воды, а не переносится вдоль волны.

Чтобы лучше понять механизм волны, рассмотрим опять идеализированный эксперимент. Предположим, что огромное пространство сплошь заполнено водой или воздухом, или какой-либо другой «средой». Где-то в центре имеется шар (рис. 36). В начале эксперимента никакого движения нет вовсе. Вдруг шар начинает ритмически «дышать», расширяясь и сжимаясь в объеме, однако все время оставаясь сферическим по форме. Что происходит в среде? Начнем рассмотрение в тот момент, когда шар начинает расширяться. Частицы среды, находящиеся в непосредственной близости к шару, отталкиваются, так что плотность прилегающего к шару слоя воды или воздуха увеличивается против своего нормального значения. Точно так же, когда шар сжимается, то плотность той части среды, которая непосредственно окружает шар, будет уменьшаться. Эти изменения плотности распространяются во всей среде. Частицы, составляющие среду, проделывают лишь малые колебания, но движение в целом – это движение поступательной волны. Существенно новым здесь является то, что впервые мы рассматриваем движение чего-то, что есть не вещество, а энергия, распространяющаяся в веществе.

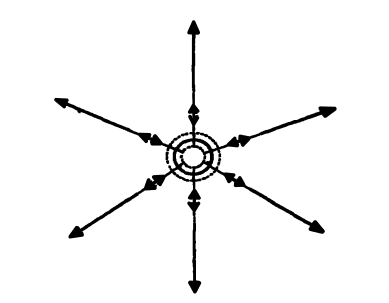
Рис. 36.

Применяя пример пульсирующего шара, мы можем ввести два общих физических понятия, важных для характеристики волн. Первое – это скорость, с которой распространяется волна. Она будет зависеть от среды и, например, различна для воды и воздуха. Второе понятие – длина волны. В волнах на поверхности моря или реки длина волны – это расстояние от углубления одной волны до углубления следующей или же расстояние от гребня одной волны до гребня следующей. Морские волны имеют большую длину волны, чем волны на реке. В наших волнах, образующихся благодаря пульсации шара, длина волны – это расстояние, взятое в некоторый определенный момент между двумя соседними шаровыми слоями, у которых одновременно плотность имеет максимальное или минимальное значение. Очевидно, что это расстояние зависит не только от среды. Большое влияние будет, конечно, иметь быстрота пульсации шара; так, длина волны будет короче, если пульсация становится быстрее, и длиннее, если пульсация медленнее.

Это понятие волны оказывается очень удачным в физике. Оно является определенно механическим понятием. Явление сводится к движению частиц, которые, согласно кинетической теории, образуют вещество. Таким образом, всякая теория, которая употребляет понятие волны, может, вообще говоря, считаться механической теорией. В частности, объяснение акустических явлений существенно опирается на это понятие. Колеблющиеся тела, например такие, как голосовые связки или скрипичные струны, являются источниками звуковых волн, которые распространяются в воздухе, аналогично тому, как это имеет место для волн, образующихся от пульсирующего шара. Вот так, с помощью понятия волны, можно все акустические явления свести к механическим.

Уже было подчеркнуто, что мы должны отличать друг от друга движение частиц и движение самой волны, которая является состоянием среды. Оба движения совершенно различны, но очевидно, что в нашем примере пульсирующего шара оба движения происходят вдоль одной и той же прямой. Частицы среды колеблются в небольших пределах, и плотность увеличивается и уменьшается периодически в соответствии с этим движением. Направление, в котором распространяются волны, и направление, вдоль которого совершаются колебания, одно и то же. Волны этого типа называются продольными. Но является ли этот тип волн единственным? Для наших дальнейших рассуждений важно ясно представить себе возможность другого типа волны, которая называется поперечной.

Изменим наш предыдущий пример. Пусть мы по-прежнему имеем шар, но он погружен в среду другого рода: вместо воздуха или воды взято нечто вроде студня или желе. Больше того, шар больше не пульсирует, а поворачивается на небольшой угол сначала в одном направлении, а затем в обратном, всегда с одним и тем же ритмом и вокруг определенной оси (рис. 37). Желе прилипает к шару, и прилипающие частицы вынуждены повторять его движение. Эти частицы вынуждают частицы, расположенные немного дальше, повторять то же движение и т. д., так что в среде возникает волна. Если мы помним о различии между движением среды и движением волны, то мы видим, что в данном случае они явно не совпадают. Волна распространяется в направлении радиуса шара, а частицы среды движутся перпендикулярно к этому направлению. Следовательно, мы создали поперечную волну.

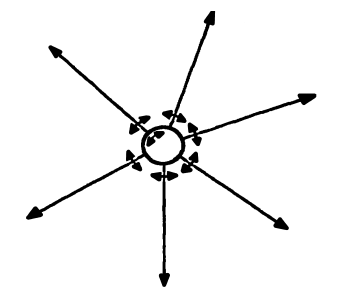
Рис. 37.

Волны, распространяющиеся на поверхности воды, поперечны. Плавающая пробка движется вверх и вниз, а волна распространяется вдоль горизонтальной плоскости. С другой стороны, звуковые волны дают нам наиболее известный пример продольных волн.

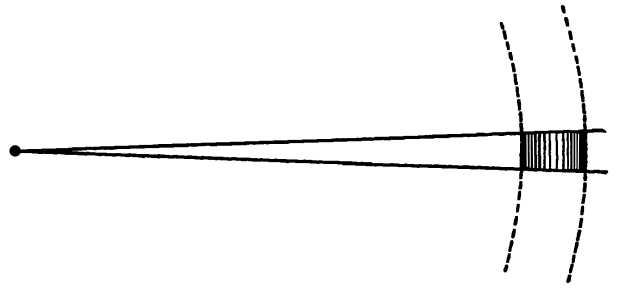
Рис. 38.

Еще одно замечание: волна, созданная пульсирующим или колеблющимся в однородной среде шаром, – это сферическая волна. Она называется так потому, что в любой данный момент все точки среды, размещающиеся на любой сфере, окружающей источник, ведут себя одинаковым образом. Рассмотрим часть такой сферы на большом расстоянии от источника (рис. 38). Чем дальше от источника мы берем такую часть сферы и чем меньшую часть мы берем, тем больше она похожа на часть плоскости. Не стремясь быть слишком строгими, мы можем сказать, что нет существенного различия между частью плоскости и частью сферы, радиус которой достаточно велик. Очень часто мы говорим о небольших частях сферической волны, далеко продвинувшейся от ее источника, как о плоских волнах. Чем дальше мы помещаем заштрихованную на рисунке часть поверхности от центра сферы и чем меньше угол между двумя радиусами, тем более она приближается к представлению о плоской волне. Понятие плоской волны, подобно многим другим физическим понятиям, есть не больше, как абстракция, которую мы можем осуществить лишь с известной степенью точности. Тем не менее это – полезное понятие, и оно нам понадобится в дальнейшем.