Волновая теория света

Вспомним, почему мы прекратили описание оптических явлений. Нашей целью было ввести другую теорию света, отличную от корпускулярной, но также пытающуюся объяснить ту же область фактов. Чтобы сделать это, мы должны были прервать наш рассказ и ввести понятие волн. Теперь мы можем вернуться к нашему предмету.

Первым, кто выдвинул совершенно новую теорию света, был современник Ньютона – Гюйгенс. В своем трактате о свете он писал:

«Если, кроме того, свет употребляет для своего прохождения некоторое время, – что мы сейчас проверим, – то из этого следует, что это движение, сообщенное окружающей материи, следует одно за другим во времени; поэтому оно, подобно звуку, распространяется сферическими поверхностями и волнами; я называю их волнами по тому сходству, которые они имеют с волнами, образующимися на воде, когда в нее брошен камень, и представляющими собой последовательно расширяющиеся круги, хотя они и возникают от другой причины и находятся лишь на плоской поверхности».

По Гюйгенсу, свет – это волна, передача энергии, а не субстанции. Мы видели, что корпускулярная теория объясняет многие наблюденные факты. В состоянии ли это сделать и волновая теория? Мы должны снова поставить те вопросы, на которые уже дали ответ с помощью корпускулярной теории, чтобы увидеть, может ли волновая теория ответить на них с таким же успехом. Сделаем это здесь в форме диалога между Н. и Г., где Н. – собеседник, убежденный в справедливости корпускулярной теории Ньютона, а Г. – убежденный в справедливости теории Гюйгенса. Ни тому, ни другому не разрешено применять доводов, полученных после того, как работа обоих великих мастеров была закончена.

Н. В корпускулярной теории скорость света имеет вполне определенный смысл. Это – скорость, с которой корпускулы движутся в пустом пространстве. Что она означает в волновой теории?

Г. Конечно, она означает скорость световой волны. Всякому известно, что волна распространяется с некоторой определенной скоростью, и то же должно быть с волнами света.

Н. Это не так просто, как кажется. Звуковые волны распространяются в воздухе, морские волны в воде. Каждая волна должна иметь материальную среду, в которой она распространяется. Но свет проходит через вакуум, в то время как звук не проходит. Предположить волну в пустом пространстве фактически означает вовсе не предполагать никакой волны.

Г. Да, это трудность, хотя и не новая для меня. Мой учитель изучал ее очень внимательно и решил, что единственный выход – предположить существование гипотетической субстанции, эфира, – передающей среды, заполняющей всю вселенную. Вселенная, так сказать, погружена в эфир. Если у нас есть смелость ввести это понятие, то все становится ясным.

Н. Но я возражаю против такого предположения. Вопервых, оно вводит новую гипотетическую субстанцию, а мы уже имеем слишком много субстанций в физике. Имеется также и другое основание против него. Вы не сомневаетесь в том, что мы должны все объяснять в пределах механики. А как относительно эфира? В состоянии ли вы ответить на простой вопрос о том, как эфир построен из своих элементарных частиц и как он обнаруживается в других явлениях?

Г. Ваше первое возражение, конечно, справедливо. Но, вводя некий искусственный невесомый эфир, мы сразу отделываемся от гораздо более искусственных световых корпускул. Мы имеем только одну «таинственную» субстанцию вместо бесконечного числа их, соответствующего огромному числу цветов в спектре. Не кажется ли вам, что это и есть настоящий прогресс? По крайней мере все трудности сконцентрированы в одном пункте. Мы не нуждаемся больше в искусственном предположении, что частицы, относящиеся к различным цветам, движутся с одной и той же скоростью в пустом пространстве. Ваше второе возражение тоже справедливо. Мы не можем дать механического объяснения эфира. Но нет никакого сомнения в том, что дальнейшее изучение оптических и, может быть, других явлений обнаружит его структуру. В настоящее время мы должны ожидать новых экспериментов и заключений, но я надеюсь, что, в конце концов, мы будем в состоянии разрешить проблему о механической структуре эфира.

Н. Оставим на время этот вопрос, так как он не может быть разрешен теперь. Мне хотелось бы видеть, как ваша теория, даже если мы отбросим трудности, объясняет те явления, которые так ясны и понятны в корпускулярной теории. Возьмем, например, тот факт, что световые лучи проходят в вакууме или в воздухе вдоль прямых. Кусок бумаги, помещенный перед свечой, создает четкую и резко очерченную тень на стене. Резкие тени были бы невозможны, если бы волновая теория была правильна, ибо волны огибали бы края бумаги и тем самым размазывали бы тень. Маленькое судно не является препятствием для морских волн, как вы знаете; они просто огибают его, не отбрасывая тени.

Г. Это не убедительный довод. Возьмите короткие волны на реке, ударяющие о борт большого корабля. Волны, возникающие на одной стороне корабля, не будут видны на другой. Если волны достаточно малы, а корабль достаточно велик, появляется очень четкая тень. Очень возможно, что свет кажется нам проходящим по прямым линиям лишь потому, что его длина волны очень мала в сравнении с величиной обычных препятствий и отверстий, употребляемых в экспериментах. Возможно, что, если бы мы могли создать достаточно малые препятствия, то никакой тени не было бы. Мы можем встретиться с большими экспериментальными трудностями в конструкции приборов, которые могли бы показать, в состоянии ли свет огибать препятствия. Тем не менее, если бы такой эксперимент можно было осуществить, он был бы решающим в борьбе между волновой и корпускулярной теориями света.

Н. Волновая теория может привести к новым фактам в будущем, но я не знаю каких-либо данных, убедительно ее подтверждающих. Пока с полной определенностью не доказано экспериментально, что свет может огибать препятствия, я не вижу какого-либо основания отказываться от корпускулярной теории, которая кажется мне проще и потому лучше, чем волновая.

На этом мы можем прервать диалог, хотя предмет его никоим образом не исчерпан.

Остается еще показать, как волновая теория объясняет преломление света и многообразие цветов. Как мы знаем, корпускулярная теория в состоянии дать такое объяснение. Мы начнем с преломления, но сначала будет полезно рассмотреть пример, не имеющий ничего общего с оптикой.

Пусть по большому открытому пространству прогуливаются два человека, держащие между собой твердый прут. Вначале они идут прямо вперед, оба с одинаковой скоростью. Пока их скорости одинаковы, велики они или малы – безразлично, прут будет совершать параллельное перемещение, то есть он не будет поворачиваться или изменять свое направление. Все последовательные положения прута параллельны друг другу. Но представим себе теперь, что в течение очень короткого времени, может быть, равного долям секунды, движения обоих людей стали неодинаковыми. Что произойдет? Ясно, что в течение этого времени прут будет поворачиваться, так что он не будет больше перемещаться параллельно своему первоначальному положению. Когда опять возобновится движение с равными скоростями, оно будет иметь направление, отличное от первоначального. Это ясно показано на рисунке 39. Изменение направления происходит в течение того промежутка времени, в котором скорость обоих пешеходов была различной.

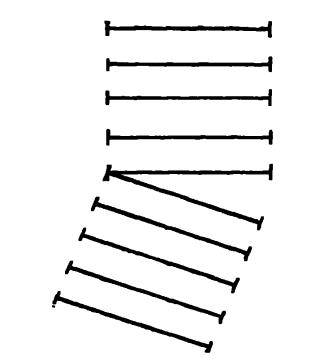
Рис. 39.

Этот пример позволит нам понять преломление волны. Плоскость волны, движущейся в эфире, ударяется о поверхность стекла. На следующем рисунке 40 мы видим волну с сравнительно широким фронтом, который перемещается вперед. Фронт волны – это плоскость, в которой в любой момент времени все части эфира находятся в одинаковом состоянии. Так как скорость зависит от среды, через которую в данный момент времени проходит свет, то скорость в стекле будет отличаться от скорости в пустом пространстве. В течение очень короткого времени, за которое фронт волны входит в стекло, различные части фронта волны будут иметь различные скорости. Ясно, что те части, которые уже достигли стекла, будут двигаться со скоростью света в стекле, в то время как другие части по-прежнему движутся со скоростью света в эфире. Благодаря этой разности в скоростях вдоль фронта волны, существующей в течение времени «погружения» в стекло, направление самой волны будет изменяться.

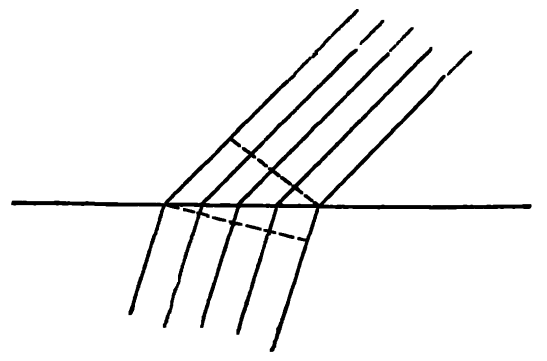
Рис. 40.

Итак, мы видим, что не только корпускулярная, но и волновая теория приводит к объяснению преломления. Дальнейшее рассмотрение и некоторое применение математики показывают, что объяснение волновой теории проще и лучше и что следствия из нее находятся в полном согласии с наблюдением. В самом деле, количественные методы рассмотрения позволяют нам вывести скорость света в преломляющей среде, если мы знаем, как преломляется луч, когда он входит в нее. Прямые измерения блестяще подтверждают эти предсказания, а тем самым и волновую теорию света.

Остается еще вопрос о цвете.

Необходимо вспомнить, что волна характеризуется двумя числами – ее скоростью и длиной. Весьма существенным является следующее утверждение волновой теории света: волны различной длины соответствуют различным цветам. Длина волны однородного желтого света отлична от длины волны синего или фиолетового. Вместо искусственного разделения корпускул, относящихся к разным цветам, мы имеем естественное различие по длине волны.

Отсюда следует, что эксперименты Ньютона по дисперсии света могут быть описаны двумя различными языками – языком корпускулярной теории и языком волновой теории. Например:

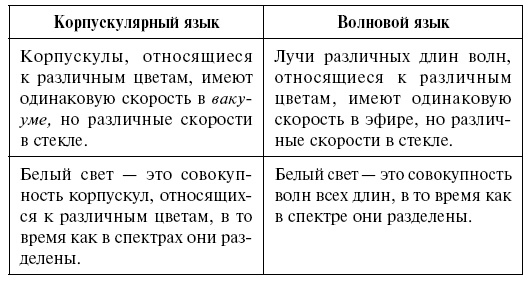
Кажется, было бы мудрым избежать двусмысленности, происходящей из факта существования двух различных теорий одних и тех же явлений, решив в пользу одной из них после внимательного рассмотрения достоинств и недостатков каждой. Диалог между Н и Г показывает, что это нелегкая задача. Решение с этой точки зрения было бы скорее делом вкуса, чем научного убеждения. Во времена Ньютона и в течение свыше ста лет спустя большинство физиков предпочитало корпускулярную теорию.

История вынесла свой приговор – в пользу волновой теории и против корпускулярной – гораздо позднее, в середине девятнадцатого столетия. Н. в своем разговоре с Г. заявлял, что в принципе возможно было экспериментальное решение спора между обеими теориями. Корпускулярная теория не разрешает свету огибать препятствия и требует наличия четких теней. С другой стороны, согласно волновой теории достаточно малые препятствия не будут отбрасывать никакой тени. В работах Юнга и Френеля этот результат был получен экспериментально, там же были сделаны теоретические выводы.

Мы уже обсуждали чрезвычайно простой эксперимент, в котором экран с отверстием помещался перед точечным источником света, а тень отбрасывалась на стену. В дальнейшем мы упростим эксперимент, полагая, что источник испускает однородный свет. Для получения наилучших результатов источник света должен быть сильным. Представим себе, что отверстие в экране делается все меньше и меньше. Если в нашем распоряжении есть сильный источник и нам удается сделать отверстие достаточно малым, то обнаруживаются новые и удивительные явления, совершенно непонятные с точки зрения корпускулярной теории. Нет больше резкого различия между светом и темнотой. Свет постепенно блекнет, переходя в темный фон через серию светлых и темных колец. Появление колец очень характерно для волновой теории. Объяснение чередования светлых и темных полос будет ясно в случае несколько иной экспериментальной установки. Предположим, что мы имеем лист черной бумаги с двумя булавочными дырочками, через которые может проходить свет. Если дырочки близко примыкают друг к другу и очень малы и если однородный свет достаточно силен, то на стене появится множество светлых и темных полос, постепенно ослабевающих и переходящих в темный фон. Объяснение очень простое. Темная полоса появляется там, где впадина волны от одной дырочки встречается с гребнем волны от другой, так что обе погашаются. Полоса света – там, где встречаются две впадины или два гребня от волн, идущих от обеих дырочек, и усиливают друг друга. Сложнее объяснение темных и светлых колец в предыдущем примере, в котором мы применяли экран с одним отверстием, но принципиально оно то же самое. Это появление темных и светлых полос при прохождении света через два отверстия и темных и светлых колец при прохождении одного отверстия следует иметь в виду, ибо позднее мы вернемся к обсуждению обеих различных картин.

Описанные здесь эксперименты обнаруживают дифракцию света – отклонение света от прямолинейного распространения, когда на пути световых волн расположены малые отверстия или препятствия (см. фото на стр. 127).

С небольшой помощью математики мы в состоянии пойти гораздо дальше. Можно установить, как велика, вернее, как мала должна быть длина волны, чтобы создать индивидуальную картину дифракции. Таким образом, описанные эксперименты позволяют нам определить длину волны однородного света. Чтобы дать представление о том, как малы эти величины, мы укажем длины волн крайних лучей видимого солнечного спектра, т. е. длины волн красного и фиолетового лучей.

Длина волны красного света равна 0,00008 сантиметра.

Длина волны фиолетового света равна 0,00004 сантиметра.

Мы не должны удивляться, что эти величины очень малы. Точно очерченная тень, т. е. явление прямолинейного распространения света, наблюдается в природе лишь потому, что обычно встречающиеся отверстия и препятствия чрезвычайно велики по сравнению с длиной волны света. Свою волновую природу свет обнаруживает лишь тогда, когда применяются очень малые отверстия и препятствия.

Но история поисков теории света никоим образом не окончена. Приговор девятнадцатого столетия не был последним и окончательным. Для современных физиков вся проблема выбора между корпускулами и волнами существует вновь, теперь уже в гораздо более глубокой и сложной форме. Примем поражение корпускулярной теории света до тех пор, пока мы не столкнемся с проблематичностью характера победы волновой теории.