«Ястребы и голуби» с большей ценой конфликта

Процессы эволюции еще интересней в ситуациях, где цена конфликта (С) очень высока по сравнению с ценностью желанной добычи. Предположим, что С = 24, а ценность добычи по-прежнему равна 20.

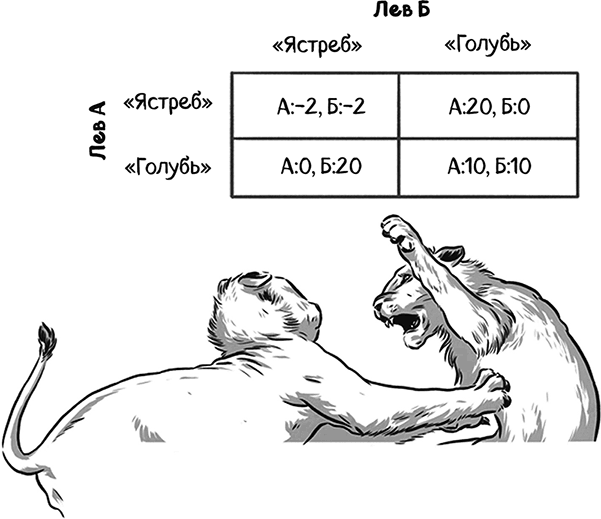
Высокая цена поражения в схватке значительно изменяет способность животного с поведением «ястреба» к выживанию и произведению потомства.

Предположим, что изначально часть популяции, условно названная «p», была запрограммирована на очень агрессивное поведение «ястреба». Оставшаяся часть популяции «(1-р)» перенимает линию поведения «голубя». Часть популяции «р» может опускаться до нуля (все животные в этой популяции – «голуби») или подниматься до единицы (все животные в этой популяции – «ястребы»).

«Голубь» ни за что не ввяжется в схватку с большой ценой, это та же самая ситуация, что и в случае с меньшей ценой конфликта. Однако было бы полезно более детально рассмотреть его ожидаемую эволюционную приспособленность.

«Голубь» вступает в схватку со случайным членом популяции. Это животное окажется «ястребом» с вероятностью «р». В этом случае противник получит добычу, а «голубь» не выиграет ничего.

Однако это животное может оказаться тоже «голубем», вероятность этого равна (1-р). В этом случае не будет физической схватки, и у животных будут равные шансы на победу. «Голубь» получает выигрыш в размере 10.

Таким образом ожидаемая эволюционная приспособленность «голубя» равняется сумме вероятности встречи с каждым из двух противников, умноженная на выигрыш в случае встречи:

Рассмотрим ситуацию с «ястребом»: это животное вступает в агрессивную схватку без страха за свою безопасность.

Вероятность того, что «ястреб» будет бороться с другим «ястребом», равна «р». Цена конфликта так высока, что перевешивает выгоду от желанной добычи, поэтому оба животных получат выигрыш в размере –2.

Вероятность того, что «ястреб» окажется в паре с «голубем», равна (1-р). Этот противник не станет вступать в схватку с агрессивным «ястребом», так что «голубь» получает весь выигрыш без физического боя и его выигрыш составляет 20.

Таким образом, ожидаемая эволюционная приспособленность «ястреба» равняется сумме вероятности встречи с каждым из двух противников, умноженная на выигрыш в случае встречи:

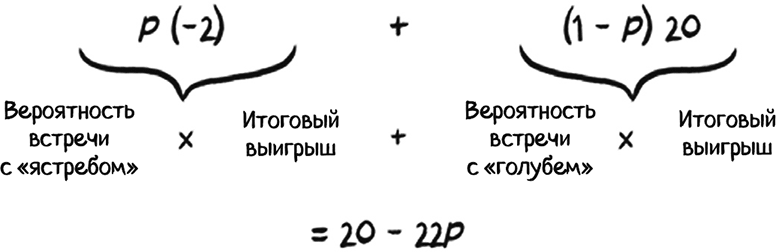
С помощью расчетов, приведенных на последних двух страницах, можно сказать, что ожидаемая эволюционная приспособленность «ястреба» выше, чем у «голубя», если:

20 – 22р > 10 – 10р

или

10 > 12 р

->

10/12 > р

->

5/6 > p

Если часть популяции, запрограммированная на поведение «ястреба» (р), меньше ⅚, то вероятность встречи двух «ястребов» и их схватки настолько мала, что ее перевешивает выгода от получения всего выигрыша при встрече с «голубем». Таким образом, со временем часть популяции «ястребов» (р) увеличится благодаря силам эволюции.

Если особей с поведением «ястреба» в популяции больше ⅚ (то есть, если р > ⅚), то «голуби» будут выживать и размножаться в больших количествах, чем «ястребы», так что часть популяции, запрограммированная на поведение «ястребов», (р) уменьшится.

В долгосрочной перспективе силы эволюции спровоцируют изменение в количестве особей каждого типа. Численность «ястребов» будет стремиться к ⅚ от всей популяции, а «голубей» – к ⅙. Мы имеем дело с такими точными пропорциями благодаря числам, которые мы указывали в платежной матрице. Однако как только цена конфликта станет выше ценности желанной добычи, эволюционные силы внесут свои коррективы в популяцию и заставят «голубей» и «ястребов» сосуществовать.

В долгосрочной перспективе «ястребы» и «голуби» будут сосуществовать в рамках одной популяции в соотношении 5 к 1, при этом оба вида в среднем будут нормально функционировать. При столкновении с «голубями» «ястребы» будут присваивать все ресурсы, но возможность серьезных увечий для них будет очень высока при схватке с другими «ястребами». «Голуби» не смогут удержать ресурсы, когда окажутся в паре с «ястребами», но никогда не пострадают в бою.

Такое долгосрочное эволюционное «устойчивое состояние», при котором количество «ястребов» в популяции равно ⅚, называется эволюционно стабильным равновесием. Это такое равновесие, которое сохраняет свою стабильность, даже если мы добавляем к одной группе животных некое количество особей, запрограммированных по-другому, в силу того, что эволюционные силы рано или поздно восстанавливают равновесие.

Вообще в эволюционных играх может быть множество исходов. В «Ястребах и голубях» наблюдается единственное эволюционно стабильное равновесие, а долгосрочное устойчивое состояние рано или поздно будет восстановлено, вне зависимости от того, сколько запрограммированных по-другому особей мы добавим.

Однако в некоторых играх возможно более чем одно эволюционно стабильное равновесие. В таких играх силы эволюции восстановят пропорции равновесия, если наблюдаются незначительные изменения в популяции. Но крупные изменения в составе популяции могут повлечь за собой совсем иное равновесие.

Некоторые игры вообще не имеют эволюционно стабильного равновесия. В таких играх популяция никогда не добьется стабильного устойчивого состояния. Наоборот, она окажется под влиянием цикличных изменений, при которых группы различных видов животных будут бесконечно то увеличиваться, то уменьшаться.