Эволюционная стабильность как усовершенствование равновесия
Интересно то, что эволюционно стабильное соотношение «ястребов» к остальной популяции (⅚) также было бы равно равновесной вероятности в равновесии Нэша в смешанных стратегиях, если бы животные выбирали стратегии рационально. И это не совпадение. Чтобы рассчитать равновесные вероятности в равновесии Нэша в смешанных стратегиях, мы должны найти такие вероятности, при которых игрокам безразлично, что выбрать – линию поведения «ястреба» или «голубя». В равновесии ожидаемые ценности обеих стратегий равны.
В «Ястребах и голубях» мы имеем дело с таким же уровнем ожидаемой эволюционной приспособленности обоих видов животных в эволюционно стабильных равновесных соотношениях. Если бы их приспособленность различалась, силам эволюции пришлось бы выделить один вид животных, существование которого было бы намного более благоприятным, чем у другого, вплоть до момента, когда было бы достигнуто устойчивое состояние.

В «Ястребах и голубях» эволюционно стабильное равновесие создает соотношение «ястребов» и «голубей» в рамках популяции, что похоже на интерпретацию равновесия Нэша в смешанных стратегиях в игре «Уклонение от уплаты налогов». В том случае равновесие создавало соотношение уклонистов и законопослушных налогоплательщиков, а решения, которые принимали игроки, были рациональными.
Когда речь идет об эволюции, концентрация на эволюционно стабильном равновесии разумна, так как она позволяет исключить равновесие, которое не выдержало бы и малейших изменений в популяции.

Игры с последовательными ходами
Часто так случается, что игроки могут проследить действия своих оппонентов перед принятием собственного решения. В некоторых играх существует порядок, в котором участники делают ходы. Они называются играми с последовательными ходами. В большинстве настольных игр, вроде шахмат, игроки совершают ходы последовательно, один за другим.
К примеру, предприниматель размышляет, стоит ей открывать кафе на определенном перекрестке или нет. При этом она может учитывать, какие магазины уже открыты поблизости, а также попробует предугадать, какие еще магазины появятся там в будущем, если она все-таки откроет там кафе.

Игры с последовательными ходами динамичны, то есть игроки могут принимать свои решения, базируясь на изучении предыдущих действий соперников и на ожиданиях их будущих действий. Участники пытаются предугадать, что их оппоненты предпримут в ответ на их возможные действия, и затем, разворачивая эту цепочку с конца, принимают решение.

Динамичная версия игры «Битва полов»
Мы можем рассмотреть трудности, которые возникают в играх с последовательными ходами, с помощью динамичной версии игры с одновременными ходами. Тут нам пригодится «Битва полов».
В обычной «Битве полов» Боб и Эми должны принять решение о планах на вечер поодиночке и одновременно. Они хотят провести вечер вместе, но им нравятся разные занятия. Помните стратегическую форму первой «Битвы полов»?

А теперь давайте немного изменим их историю. Предположим, что рабочий день Эми заканчивается на час раньше рабочего дня Боба. Она идет к месту проведения одного из занятий и звонит Бобу, чтобы сообщить, где находится. Как только она позвонила ему, у нее больше нет возможности поменять свое местоположение, но Боб пока может пойти на стадион или в танцевальный класс.

Расширенная форма игры
Эми делает первый ход, а Боб ходит вторым и учитывает выбор Эми. Нам больше ни к чему стратегическая форма игры, ведь она нужна была нам, когда игроки делали одновременные ходы, а стратегическая форма не фиксирует порядок принятия решений. Тут нам пригодится новая диаграмма, которая послужит иллюстрацией игры с последовательными ходами: представление расширенной формы, также известное как игровое дерево.
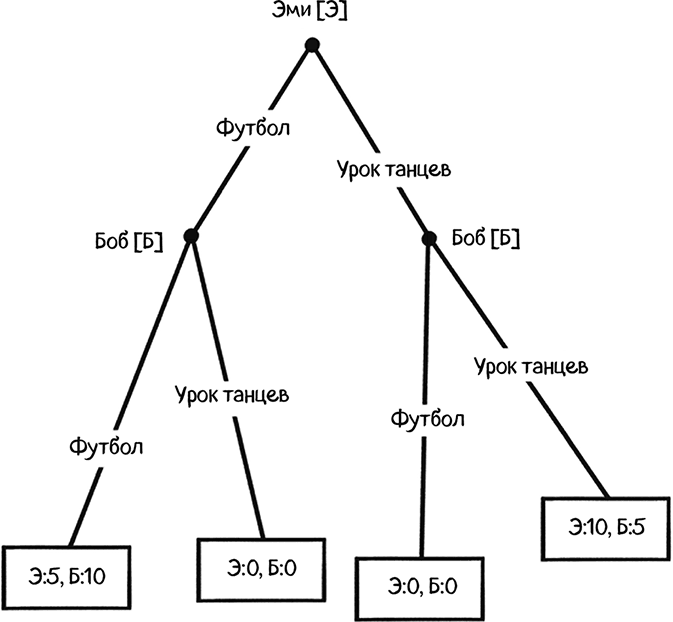
Расширенная форма вводит порядок возможных выборов с помощью точек принятия решения (то есть точек, которые указывают момент принятия решения).
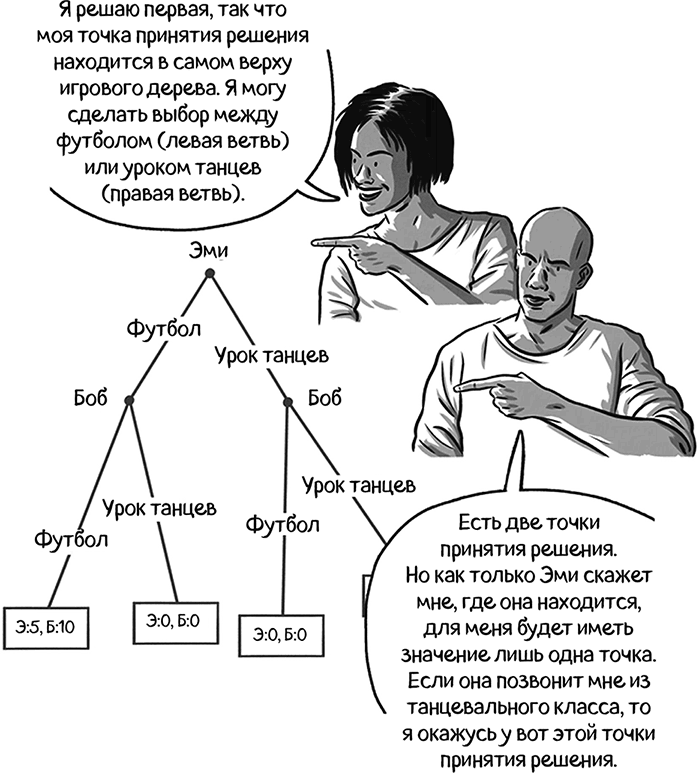
Когда Эми принимает свое решение, она знает, что Боб проследит ее выбор до принятия своего решения. Она также знает, что ее выбор повлияет на его выбор. Поэтому она постарается предугадать, как он отреагирует на каждый из ее возможных выборов.
Равновесие, совершенное по под-играм
Если бы Эми позвонила Бобу с футбольного стадиона, то для Боба имела бы значение лишь левая нижняя ветвь дерева. Так что мы может рассмотреть игру саму по себе с этой точки, которая называется «под-игра». Начиная с этого момента, Боб просто будет стараться сделать все от него зависящее.
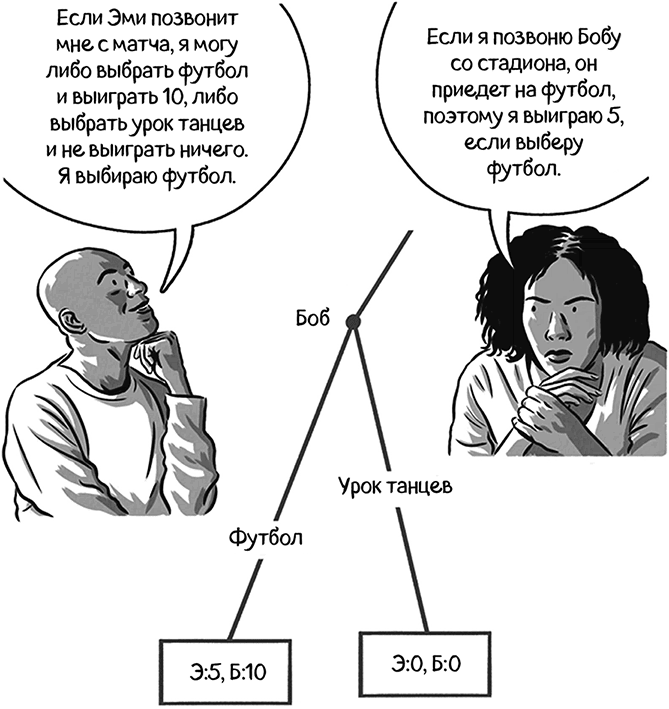
Эми также попробует предугадать, как поступит Боб, если она решит пойти на танцы. Если она позвонит Бобу из танцевального класса, Бобу пришлось бы играть в другую под-игру (правая ветвь расширенной формы).
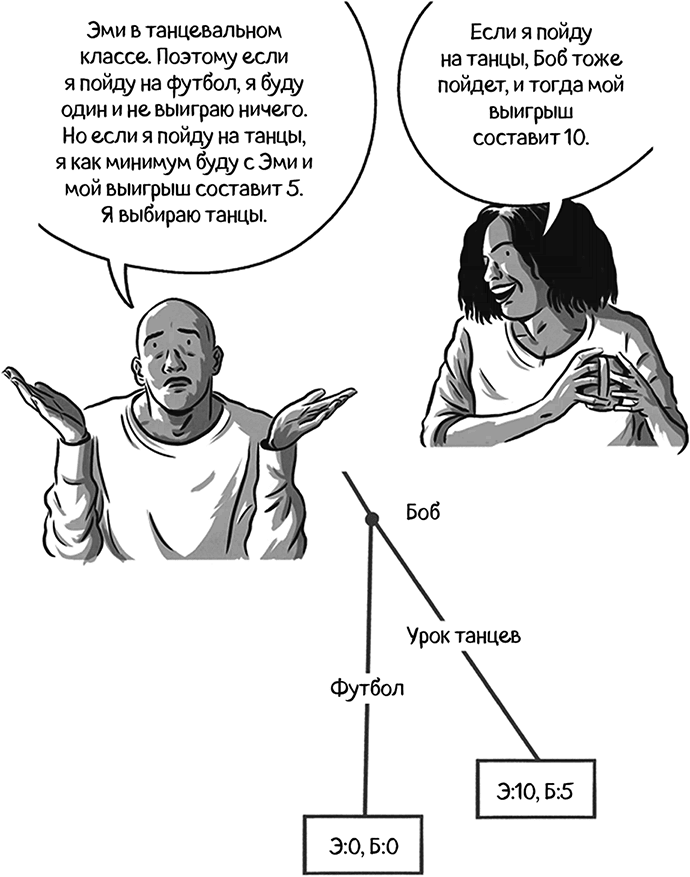
Динамическая игра Эми и Боба может быть разрешена с помощью обратной индукции. Эми предугадывает, что произойдет в конце игры, и распутывает всю игровую цепочку оттуда, пытаясь понять, каким будет ее оптимальный выбор.
С точки зрения Эми было бы рациональным пойти танцевать, так как она знает, что Боб присоединится к ней. Это равновесие, совершенное по под-играм: игроки делают оптимальные для них обоих выборы в каждой под-игре изначальной игры. Равновесие, совершенное по под-играм, означает, что игроки концентрируются на будущем. На каждой точке принятия решения они делают все возможное, не тая обид за прошлые действия.
В этой игре равновесие, совершенное по под-играм, особенно выгодно для Эми. Здесь проявляется преимущество первого хода.

Однако не все игры с последовательными ходами имеют такую черту, как преимущество первого хода. Существует множество игр, в которых первый ход ставит игрока в сложное положение.

