Глава 6
Музей Всех Возможных Раковин

Эволюция продвигается к вершинам горы Невероятности под давлением естественного отбора. Понятие давления в данном случае подходит как нельзя лучше. Слова “давление отбора” вызывают почти физическое ощущение того, как вид толкают вверх по склону, так что он просто вынужден эволюционировать. Мы говорим, что хищники создали давление естественного отбора, под воздействием которого у антилоп эволюционировала способность бегать быстрее. Но при этом мы понимаем, что имеется в виду на самом деле: вероятность того, что в желудках хищников перевариваются гены, связанные с развитием коротких ног, относительно выше, а следовательно, коротконогих антилоп в природе становится меньше. “Давление” со стороны разборчивых самочек стимулирует самцов фазанов одеваться в яркие перья. Это означает, что у гена, необходимого для красоты оперения, неплохие шансы проникнуть вместе со спермой в организм самки. Но, по нашей теории, самцы становятся красивее под “давлением” естественного отбора. Однако расфуфыренные фазаны обращают на себя взгляды не только своих подруг, но и врагов, поэтому хищники, безусловно, создают противодействующее “давление отбора”, которое заставляет птиц быть поскромнее. Не будь хищников, петухи ради самок обретали бы все более и более броскую окраску. Таким образом, давление естественного отбора с разных сторон может вызывать как противоположные эффекты, так и параллельные и даже (математики показали бы это наглядно) направленные под углом друг к другу. Более того, давление естественного отбора может быть “сильным” и “слабым” – понятные и привычные эпитеты отлично отражают смысл происходящего. Ряд поколений выбирает свой путь к вершине, испытывая давление естественного отбора со всех сторон, разные силы тянут и дергают вид то дружно, то вразнобой.

Но давление – это еще не все. Легким ли будет восхождение, зависит и от профиля склонов. Помимо того, что давление отбора с разной интенсивностью подталкивает вид то туда, то сюда, есть еще и линии наименьшего сопротивления и непреодолимые препятствия. Скажем, давление естественного отбора жестко определяет направление движения вида, но если на пути встанет отвесная стена, в нее все и упрется. У естественного отбора должен быть выбор. Без генетической изменчивости любое давление бессильно. Утверждать, что антилопы стали быстрее бегать под давлением естественного отбора, созданного хищниками, равносильно утверждению, что хищники пожирают тех животных, которые бегают медленнее. Но если нет возможности выбора между генами быстроногих и медлительных антилоп – иначе говоря, если различия между ними обусловлены только особенностями окружающей среды, – эволюция тут не спасет. На горе Невероятности может не оказаться подходящего склона для подъема на уровень высоких скоростей.

Мы подходим к проблеме безнадежной неопределенности и разброса мнений среди биологов. На одном полюсе находятся те, для кого генетическая изменчивость подразумевается по умолчанию. Было бы давление естественного отбора, считают они, а подходящие генетические вариации всегда найдутся. Траектория филогенетических групп в эволюционном пространстве зависит только от взаимодействия между разнонаправленными давлениями естественного отбора. Их оппоненты на противоположном полюсе полагают, что направление эволюции определяется в первую очередь наличием доступной вариации. Кое-кто идет еще дальше, приписывая естественному отбору второстепенную роль вспомогательного агента. Можно было бы нарисовать комикс с двумя персонажами, которые спорят о том, почему у свиней нет крыльев. Убежденный селекционист уверяет, что крылья не дали бы свинье никаких преимуществ, вот она ими и не обзавелась. Крылья принесли бы свиньям пользу, возражает его противник, но не случилось мутаций с образованием зачатков крыльев, естественному отбору не с чем было работать, поэтому крылья так и не сформировались.

Даже при допущении, что у горы Невероятности может быть много вершин, в терминах нашей географической модели эту куда более сложную дилемму не описать. Нужна новая метафора, и, наверное, она понравится математикам, хотя мы обойдемся без математических символов. Это отнимет у нас побольше сил, чем гора Невероятности, но игра стоит свеч. В “Слепом часовщике” я вкратце объяснил, что именно скрывается под разными названиями – “генетическое пространство”, “страна биоморфов” и “дорожная сеть мира животных”. Не так давно философ Дэниел Деннет глубже проник в эту неизведанную область – он дал ей поэтичное название “Менделевская библиотека” по ассоциации с “Вавилонской библиотекой” Борхеса. В этой главе я предлагаю посетить грандиозный музей зоологических фантазий.

Представьте себе музей с залами, простирающимися во все стороны, а также вверх и вниз сколько хватает глаз. В его хранилищах собраны все виды животных, которые когда‐либо существовали в природе или гипотетически могли бы существовать. Каждый вид помещается рядом с теми, на кого он больше всего похож. Направление одной музейной галереи – это одно измерение, отвечающее тому или иному направлению, в котором может проявляться изменчивость животных. Скажем, если вы пойдете по какой‐нибудь галерее на север, то заметите, что у экспонатов в витринах рога становятся все более длинными. Если развернетесь и направитесь на юг, то пойдете в сторону уменьшения рогов. К востоку рога меняться не будут, зато поменяется какой‐то другой признак – например, зубы станут острее. В западной стороне зубы будут более тупыми. Размер рогов и острота зубов – это лишь два из тысяч возможных направлений изменчивости животных, поэтому галереи должны пересекаться всевозможными способами и не только в привычном для нас и нашего восприятия трехмерном пространстве. Это я и имел в виду, когда сказал, что мы должны научиться мыслить математически.

Что значит мыслить в четырехмерном измерении? Допустим, мы измеряем четыре признака для антилоп – длину рогов, остроту зубов, длину кишечника и густоту шерсти. Если не принимать во внимание один из признаков – например, густоту шерсти, – можно отвести каждой антилопе место на трехмерной диаграмме (кубике) оставшихся признаков, то есть длины рогов, остроты зубов и длины кишечника. Как теперь добавить сюда же четвертый признак – густоту шерсти? Мы должны построить отдельные кубики для короткошерстных антилоп, для тех, у кого шерсть чуть длиннее и так далее. Сначала надо поместить антилопу в кубик, отведенный для ее длины шерсти, а затем, уже в пределах этого кубика, найти точку для ее рогов, зубов и кишечника. Густота шерсти – это четвертое измерение. По такому принципу можно выстроить семейство кубиков, кубик из кубиков, кубик кубиков из кубиков – пока все животные не займут свои места в многомерном пространстве.

Чтобы вы лучше поняли суть идеи Музея Всех Возможных Животных, в этой главе мы рассмотрим отдельный случай, более или менее применимый для анализа в трехмерном пространстве. В следующей главе я вернусь к тому спору, с которого начал эту главу, и попытаюсь предложить другой стороне кое‐какие конструктивные идеи, дабы найти мирное решение (я ведь убежден в своей правоте). В этой главе мы займемся трехмерными раковинами улиток и вообще витыми раковинами. Для описания большинства основных типов раковин достаточно трех переменных, поэтому их можно изучать в трехмерном пространстве. Далее я продолжу линию известного палеонтолога из Чикагского университета Дэвида Раупа. Самого Раупа вдохновил выдающийся шотландский биолог Дарси Томпсон, профессор прославленного старинного Сент-Эндрюсского университета, автор книги “О росте и форме” (On Growth and Form), впервые опубликованной в 1919 году. Эта книга в течение почти всего двадцатого столетия, оставаясь в стороне от основного направления развития науки, тем не менее оказывала заметное влияние на зоологов. Биология несколько проиграла от того, что Дарси Томпсон скончался до наступления компьютерной эры, ибо каждая страница его великого труда просит компьютера. Рауп написал программу генерирования форм раковин, а я написал похожую программу, чтобы проиллюстрировать эту главу, хотя, разумеется, встроил ее в программу искусственного отбора, подобную той, что описана в “Слепом часовщике”.

Раковины улиток и других моллюсков, как и раковины брахиопод (которые, несмотря на явное сходство с моллюсками, не имеют с ними ничего общего), растут совершенно особым образом, и их ростовые процессы совсем не похожи на наши. Мы начинаем свой жизненный путь малышами и растем равномерно, хотя одни органы могут развиваться быстрее других. В организме человека нельзя выделить фрагмент, который сохранился бы в младенческом состоянии. А в раковинах моллюсков такие фрагменты существуют. Крошечные раковины новорожденных моллюсков нарастают по направлению от центра к периферии, по краям, так что центральный отдел взрослой раковины представляет собой “детскую” раковину. Каждая особь всю жизнь носит с собой детский кусочек себя, самое узкое место своей раковины. Раковина моллюска наутилуса, уже знакомого нам обладателя глаза-дырочки, разделена на заполненные воздухом камеры; за счет них он держится на плаву, а в одной, самой просторной и новой, последней на растущем краю, живет сам на текущий момент времени (рис. 6.1).

Из-за того, что раковины расширяются по краям, все они имеют примерно одинаковую форму – объемной логарифмической (изогональной) спирали. Не путайте логарифмическую спираль с архимедовой, по которой матрос укладывает на палубе корабельный канат. Количество витков каната не имеет значения, ширина очередного витка постоянна и равна толщине каната. В логарифмической спирали, напротив, по мере удаления от центра кривая разгибается. Одни спирали разгибаются больше, другие меньше, но одна и та же – всегда одинаково. На рис. 6.2 показаны архимедова спираль и две логарифмические, раскрытые в разной степени.

Рис. 6.1. Раковина наутилуса в разрезе. Моллюск всегда выбирает для жизни самую последнюю, новенькую камеру.

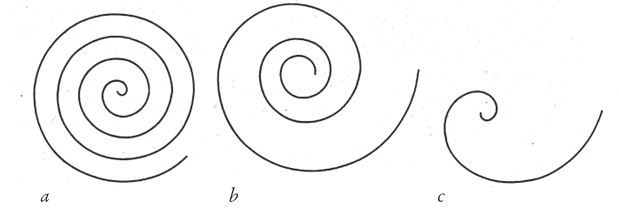
Рис. 6.2. Типы спирали: (а) архимедова; (b) логарифмическая с низкой степенью расширения; (с) логарифмическая с высокой степенью расширения.

Раковина нарастает не вдоль линии, а как труба. Для нашего случая примем, что сечение трубы круглое, хотя далеко не всегда раковина напоминает валторну. Условимся также, что спираль на рисунке – это внешняя сторона трубы. Возможен вариант, когда труба расширяется ровно так, чтобы ее внутренняя поверхность прилегала к предыдущему витку (рис. 6.3а). Но это необязательно. Если диаметр трубы увеличивается медленнее, чем раскручивается внешний край спирали, между соседними витками остается пробел, который тоже будет увеличиваться (рис. 6.3b). Чем шире пробел, тем более вероятно, что такая “разреженная” спираль подходит не улитке, а червю.

Чтобы описать форму спирали, Рауп ввел три параметра – W, D и T. Надеюсь, меня не осудят, если я назову их расширение, червячность (характеризует степень извива) и конусность. Так легче будет запомнить, какой коэффициент к какому свойству относится, чем если бы мы оперировали только буквенными обозначениями. Расширение показывает, с какой скоростью раскручивается (раскрывается) спираль. При расширении, равном 2, интервал между витками увеличивается вдвое после каждого полного оборота. Этот случай проиллюстрирован на рис. 6.2b. Спираль на рис. 6.2b с каждым новым витком удваивается в поперечном сечении. Спираль на рис. 6.2с раскручена еще сильнее – ее расширение равно 10. Если описать по этой спирали полный виток, ее общая ширина увеличится в 10 раз, хотя в природе спираль обрывается задолго до завершения витка. Скажем, расширение раковины двустворчатого моллюска сердцевидки измеряется тысячами, она раскрывается так быстро, что до настоящей спирали дело практически не доходит.

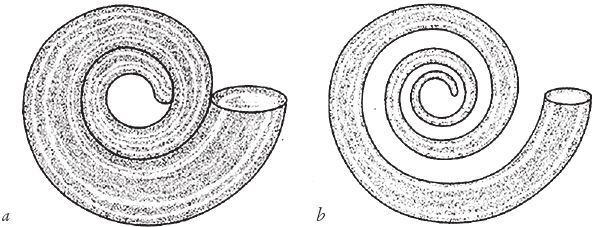
Рис. 6.3. Спирали одного типа при разных размерах трубы: (а) труба широкая, поэтому последовательные витки уложены вплотную; (b) труба узкая, поэтому между витками остается свободное пространство.

Я бы не хотел, чтобы вы решили, будто физический смысл расширения заключается в скорости увеличения диаметра трубы. Для этого есть второй параметр – червячность. Труба не всегда занимает все очерченное раскрытой спиралью пространство, поэтому нам нужен этот показатель. Раковина может быть неплотной, как на рис. 6.3b. Спирали на рис. 6.3а и 6.3b имеют одинаковое расширение (2), но для рис. 6.3b червячность больше, чем для рис. 6.3.а – 0,7 и 0,5 соответственно. Червячность 0,7 означает, что расстояние от центра спирали до внутренней границы трубы составляет 70 % расстояния от центра спирали до внешней границы трубы. Для любой части трубы, где бы вы ни измеряли внутренний и внешний радиусы, червячность постоянна (непонятно, почему так должно быть, но в природе это правило соблюдается, и по умолчанию мы будем его придерживаться). Очевидно, что при большом значении червячности – скажем, 0,99 – труба будет тонкой, почти нитевидной, так как внутренний радиус будет равен 99 % внешнего.

При какой червячности витки будут плотно прилегать друг к другу, как на рис. 6.3а? Это зависит от расширения. Точнее, критическое значение червячности для плотной спирали обратно пропорционально расширению – иначе говоря, равно единице, деленной на расширение. В обоих случаях на рис. 6.3 расширение равно 2, поэтому критическое значение червячности для плотно уложенных витков равно 0,5, что мы и имеем для спирали на рис. 6.3а. На рис. 6.3b червячность выше критической, поэтому спираль раскрыта сильнее и интервалы между витками больше. Для раковины с расширением 10, как на рис. 6.2c, критическое число червячности было бы 0,1.

Что получится при червячности, значение которой меньше критического? Мы ведь можем представить себе толстую трубу, скрученную настолько плотно, что ее витки перекрываются – спираль, как на рис. 6.3, с червячностью 0,4? Территориальный спор может быть разрешен двумя способами. Например, можно позволить новым виткам стиснуть предыдущие. Наутилус так и поступает. При этом сечение трубы будет уже не правильной окружностью, а как бы с выемкой. Но ничего страшного в этом нет: как вы помните, мы просто условились, что сечение будет круглым. Многие моллюски благополучно живут в трубах, сечение которых далеко от идеальной окружности, – ну и ладно. Иногда искаженную форму сечения проще всего списать на то, что приходится мириться с предыдущими витками.

Второй способ – подняться над плоскостью и тем самым не допустить наслаивания витков. Тут нам понадобится третий параметр спирали – высота. Представьте себе, что спираль, раскручиваясь, перемещается вдоль боковой поверхности и превращается в высокую коническую шапку. Третий параметр спирали – конусность – показывает, с какой скоростью новые витки ползут по стенкам конуса. У наутилуса конусность равна 0 – все его витки расположены на одном уровне.

Итак, мы имеем три количественные характеристики спирали – расширение, червячность и конусность (рис. 6.4). Если мы не будем учитывать какую‐нибудь из них – например, конусность, – то сможем нарисовать на листе бумаги графическую зависимость двух других. У каждой точки на диаграмме будет две координаты, присущая только ей пара расширение-червячность, и тогда мы сможем написать программу, которая нарисует нам раковину. На рис. 6.5 показаны 25 точек диаграммы, расположенные с равными интервалами. Перемещаясь по точкам слева направо, компьютерные раковины по мере возрастания червячности закручиваются сильнее. Если двигаться сверху вниз – в сторону увеличения расширения, – то спирали будут раскрываться, пока вовсе не потеряют вид спирали. Пусть расширение возрастает по логарифмическому закону – тогда точки не будут сливаться. При этом в каждой следующей точке по мере продвижения вниз мы не прибавляем к данной величине фиксированное число, как на обычном графике и как по оси червячности, а умножаем ее на определенный коэффициент – в нашем случае на 10. Это нужно для того, чтобы включить в диаграмму раковины двустворчатых моллюсков (например, сердцевидок [сем. Cardiidae] и венерок [отр. Venerida], внизу слева на рисунке); в области расширений, доходящих до нескольких тысяч, небольшой прирост не будет заметен. На разных участках диаграммы вы можете видеть фигуры, напоминающие форму раковин аммонитов, наутилуса, двустворчатых моллюсков, улиток и кольчатых червей – я отметил области, где они должны располагаться.

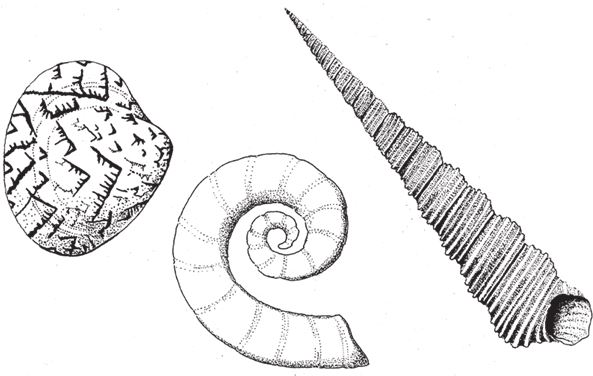
Рис. 6.4. Примеры раковин, которые показывают, что значит расширение, червячность и конусность: (а) большое расширение: двустворчатый моллюск Liconcha castrensis; (b) большая червячность: Spirula; (с) большая конусность: Turritella terebra.

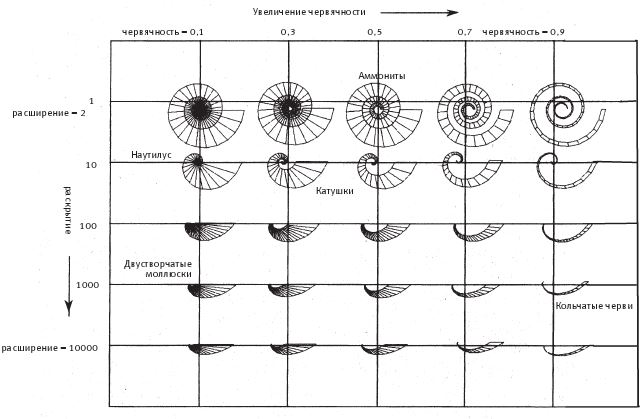
Рис. 6.5. На этой диаграмме показано, как меняются компьютерные раковины в зависимости от значений червячности и расширения. Шкала по оси расширения – логарифмическая, то есть шаг по горизонтальной оси соответствует десятикратному увеличению расширения. По оси червячности с каждым шагом значение этого параметра возрастает на определенную величину. В определенных точках диаграммы могли бы расположиться некоторые существующие в природе раковины.

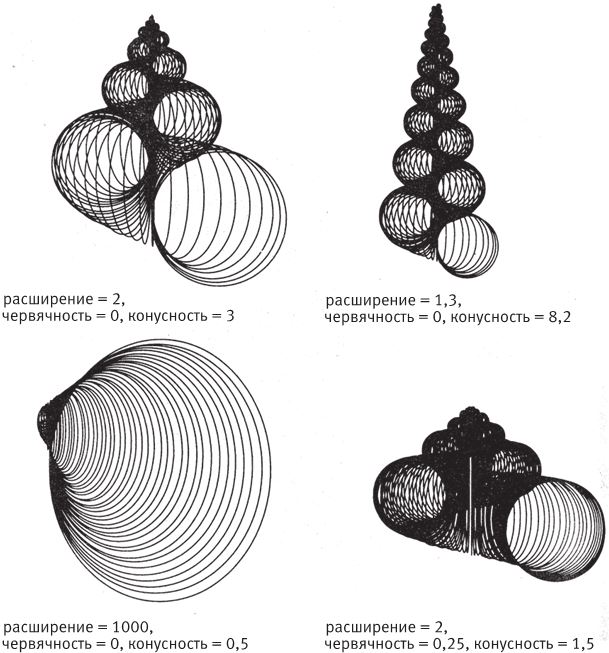
Рис. 6.6. “Рентгеновские снимки” четырех компьютерных раковин с разными значениями расширения, червячности и конусности.

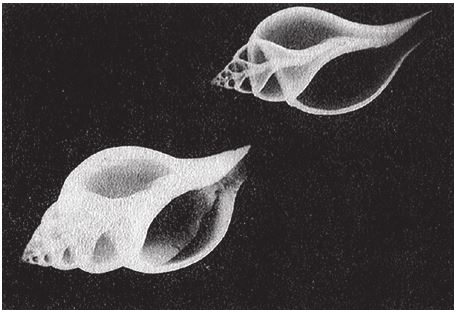
Рис. 6.7. Рентгеновские снимки живых раковин.

Мой компьютер умеет рисовать раковины в двух режимах. На рис. 6.5 раковины изображены в том режиме, где основной критерий – форма самой спирали. На рис. 6.6 раковины показаны в другом аспекте – их сечения, словно рентгеновские снимки, дают представление о форме их “твердого тела”. На рис. 6.7 приведен подлинный рентгеновский снимок настоящей раковины, который поясняет природу такой картины. Четыре раковины на рис. 6.6 – виртуальные, как и те, что изображены на рис. 6.4; я выбрал их в качестве иллюстрации для разных значений расширения, червячности и конусности.

Диаграмма на рис. 6.8 отличается от рис. 6.5 только тем, что здесь показано рентгеновское представление раковин в системе координат расширение-конусность, а не расширение-червячность.

Конечно, можно было бы составить диаграмму и в координатах червячность-конусность, но не хочется загромождать книгу. Лучше сразу перейдем к знаменитому кубику Раупа (рис. 6.9). Без учета формы сечения трубы для описания геометрии раковины достаточно трех параметров, поэтому каждую раковину можно поместить в отдельную ячейку трехмерной коробки. Так, Музей Всех Возможных Раковин в противоположность Музею Всех Возможных Тазовых Костей представляет собой самую обыкновенную башню. Каждому из трех числовых параметров раковины соответствует одно из ее ребер. Зайдите в Музей Всех Возможных Раковин и отправляйтесь для начала на север – пусть это будет ось червячности. Вы увидите, что раковины в галерее, мимо которых вы проходите, закручиваются все сильнее и сильнее, не меняясь в остальном. Если, дойдя до какой‐то точки, вы повернете налево – на запад, – то будет возрастать конусность раковин, они станут выше и острее, тогда как другие их свойства останутся прежними. И наконец, когда вам надоест бродить туда-сюда с севера на юг и с запада на восток и вы начнете подниматься строго вверх по оси расширения, раковины будут становиться все шире и шире. Прокопав ходы внутри куба под правильно выбранным углом, вы сможете попасть из одной ячейки в другую, минуя ряд раковин промежуточной формы. Любое сечение куба, взятое под любым углом, можно нарисовать на плоском листе бумаги.

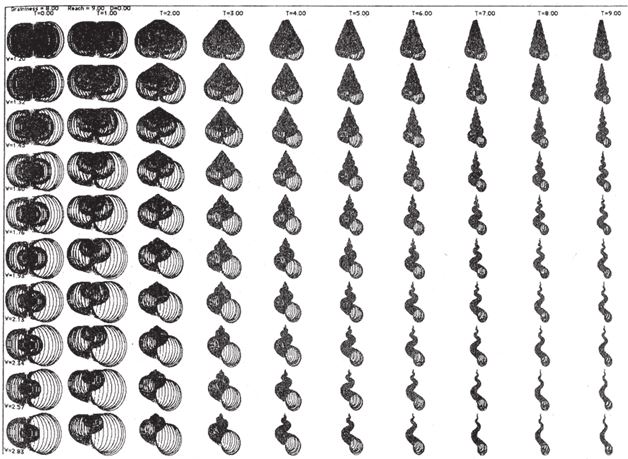
Рис. 6.8. Диаграмма компьютерных раковин в “рентгеновском” представлении, в координатах конусность (T, по горизонтальной оси) – расширение (W, по вертикальной оси). Как и на рис. 6.5 ось расширения – логарифмическая, но здесь расширение небольшое, раковины разворачиваются не слишком сильно.

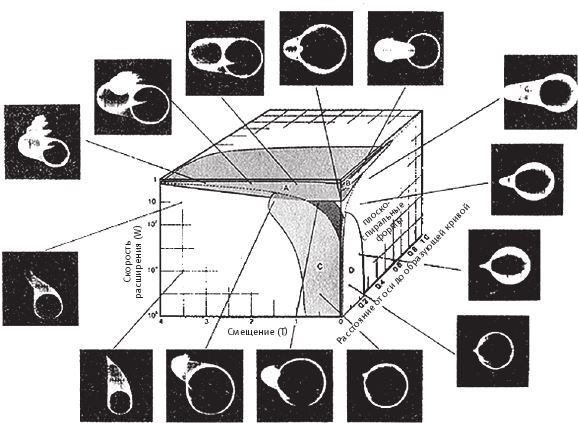
Рис. 6.9. Кубик Раупа. Рауп изобразил трехмерную диаграмму в координатах расширение (W по его терминологии, по вертикали), конусность (Т, по горизонтали), червячность (D, по оси, уходящей за плоскость рисунка). В ключевых точках диаграммы помещаются “рентгеновские снимки” компьютерных раковин. Области, где могли бы находиться настоящие раковины, выделены цветом. В незакрашенных областях располагаются гипотетически возможные формы раковин.

Программа Раупа подсказала мне идею моей собственной программы. Рауп не стал рисовать в своей публикации все раковины, что было бы крайне затруднительно, а выделил ключевые точки куба. Фигуры вокруг куба на рис. 6.9 – это теоретические раковины, которые мы можем найти в соответствующих им точках пространства. Какие‐то из них напоминают настоящие морские ракушки. Другие ни на что не похожи, но в семействе компьютерных раковин им отведены определенные места. Области, где могут располагаться существующие в природе раковины, Рауп закрасил.

Раковины аммонитов, родичей наутилуса, в былые времена многочисленных, но разделивших – неважно, по какой причине – горькую участь динозавров, были витыми. Однако, в отличие от раковин улиток, они почти всегда укладывались на плоскости. Значение конусности у них – по крайней мере, у типичных аммонитов – равнялось нулю. Но у некоторых – в частности, у рода Turrilites в меловом периоде – сформировалась более выраженная конусность, вследствие чего они независимо от других видов обрели сходство с улиткой. За исключением таких нетипичных форм аммониты заняли пространство вдоль восточной стены Музея Раковин (вы, конечно, понимаете, что термины “восток” и “запад” мы выбрали произвольно для данной диаграммы). Витрины с типичными аммонитами выстроились только на южной половине восточной стены, причем только на нескольких верхних уровнях. В галерею аммонитов вторгаются улитки и другие брюхоногие моллюски, но кроме того они уходят далеко на запад (по оси конусности) и спускаются чуть ниже по этажам кубического кондоминиума. Однако нижние этажи с относительно большими значениями расширения, где раковины быстро разворачиваются, в основном заселены двумя крупными группами животных, имеющих двустворчатую раковину. Собственно двустворчатые моллюски продвигаются чуть дальше на запад – их раковины слегка закручены, как у улиток, но выглядят иначе, потому что очень быстро раскручиваются. Брахиоподы, или плеченогие (как мы уже знаем, и не моллюски вовсе), внешне очень похожи на двустворчатых моллюсков, но у них такая же “плоская спираль”, как у аммонитов. С двустворчатыми моллюсками брахиопод роднит то, что витки их раковин полностью разворачиваются раньше, чем успевает образоваться форма, которую можно было бы назвать спиральной.

Эволюционная линия каждой конкретной группы пролегает по своему маршруту в Музее Раковин, и чтобы это проиллюстрировать, я встроил свою программу для рисования раковин в более крупную программу искусственного отбора, о которой рассказывал в “Слепом часовщике”. Просто удалил из программы “Слепого часовщика” модуль эмбрионального развития ветвлением и вставил вместо него модуль эмбрионального развития с ростом раковины. Объединенную программу я назвал “Слепой строитель”. Напомню, что раковины-соседки всегда очень похожи друг на друга, поэтому мутации эквивалентны небольшим перемещениям по “музейным залам”. В программе каждому параметру раковины отвечает один локус – ген с переменным числовым значением. Поэтому малые изменения расширения, червячности и конусности отвечают трем типам мутаций. До известной степени изменения могут быть как “полезными”, так и “вредными”. Расширение может быть не меньше 1 (иначе это было бы не расширение, а сужение); верхнего предела для расширения нет. Ген червячности принимает дробное значение от 0 до 1; единица отвечает такой тонкой и извилистой трубе, что вряд ли это вообще возможно. Конусность возможна любая, отрицательные числа говорят о том, что раковина перевернута. В центре экрана, аналогично тому, как работала исходная программа “Слепого часовщика”, помещается родительская раковина, окруженная целым выводком бесполых отпрысков со случайными мутациями – ее ближайшими соседями по Музею Раковин. Человек (селекционер) выбирает компьютерной мышкой одну из раковин для дальнейшего разведения. Перемещает ее в центр, и на экране появляется новая группа отпрысков. Селекционер может повторять этот процесс, пока не устанет. Постепенно вам начинает казаться, что вы бродите по залам Музея Всех Возможных Раковин. Вам могут встретиться знакомые экспонаты, похожие на те, что вы когда‐то подбирали на берегу моря. В другой раз вы словно выйдете за границы реальности и окажетесь в математическом мире, среди таких раковин, какие в природе не существуют.

Как я уже говорил, практически все множество раковин описывается тремя параметрами, но при одном условии, которое мы приняли для простоты, но которое может быть ошибочным, – что в сечении труба всегда круглая. Как правило, труба, расширяясь, действительно сохраняет свои очертания, но далеко не всегда она круглая. Для овального сечения в моей компьютерной модели есть четвертый “ген” – параметр форма, который измеряется отношением высоты овальной трубы к ее ширине. Круг – это крайний случай овала, форма которого равна 1. Этот ген позволяет колоссально расширить возможности модели для изображения настоящих раковин. Но и этого мало. Сечение природных раковин – вовсе не обязательно круг или овал, и они вовсе не обязаны подчиняться простым математическим правилам. На рис. 6.10 показаны раковины с отличным от окружности, фигурным сечением основной трубы, которые, кстати, занимают в нашем кубическом музее разные “витрины”.

Дополнительная переменная включается в программу легко и без затей – в виде набора предварительно нарисованных сечений разной формы. Затем каждый такой контур трансформируется – сплющивается в горизонтальном или вертикальном направлении – текущим (изменяемым) значением гена формы. Далее программа завивает трубу точно так же, как круглую, и генерирует измененные контуры. Лучше всего – и когда‐нибудь я попробую это сделать – было бы научить компьютер имитировать реальный, непостоянный процесс роста раковины вдоль направляющей линии трубы и таким образом рисовать сечения произвольной формы. Как бы то ни было, на рис. 6.11 представлен “парк” компьютерных раковин, выращенных с помощью нашей программы селекции с участием человека. Они были отобраны для размножения за сходство со знакомыми нам раковинами; для каких‐то из них можно найти аналоги на рис. 6.10, еще какие‐то напоминают ракушки, которые вы могли бы увидеть на пляже или в море, плавая под водой.

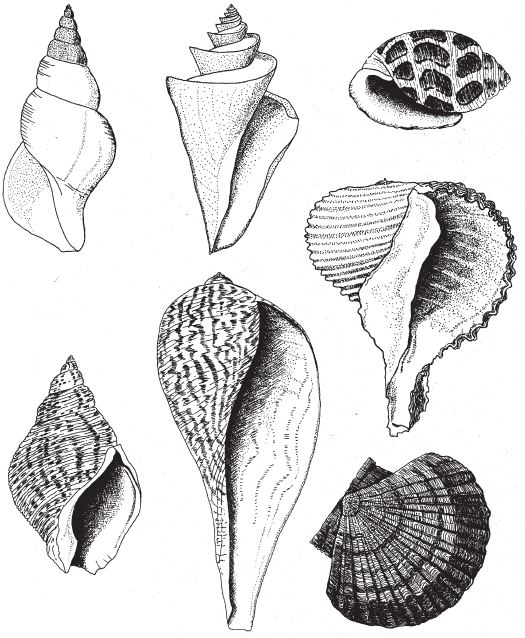
Рис. 6.10. Настоящие раковины в разрезе: (сверху слева по часовой стрелке): пятнистый нассариус, Сominella adspersa; левозакрученный нептун, Neptunia contraria; японская удивительная татчерия, Thatcheria mirabilis; брюхоногий моллюск, Acteon eloisae; рапан, Rapa rapa; большой гребешок, Peten maximus; изящный фикус, Ficus gracilis.

Рис. 6.11. Коллекция компьютерных раковин с различными сечениями, выведенных в программе “Слепой строитель”. Они были отобраны в процессе селекции по принципу внешнего сходства с существующими в природе раковинами, в частности, с некоторыми из тех, что показаны на рис. 6.10.

Форма сечения трубы может стать еще одним измерением – или комплексом измерений – в Музее Всех Возможных Раковин. Раковины с круглым сечением, если вернуться к ним и не учитывать это новое измерение, хороши в частности тем, что их легко нарисовать в трехмерном пространстве и удобно разместить в Музее Всех Вероятных Форм. Но это вовсе не означает, что в реальной жизни найдутся все экспонаты теоретической выставки. Как мы видели, в природе большая часть музейных залов пустует. Рауп выделил населенные области цветом (рис. 6.9), и такие области занимают меньше половины всего куба. К северу и к западу уходят целые галереи воображаемых, никогда не существовавших на нашей планете раковин, выращенных только в рамках данной математической модели. Почему таких раковин не бывает? И почему, раз уж мы задаемся подобными вопросами, те раковины, что когда‐либо существовали, вообще оказались в этом кубическом пространстве?

Как могла бы выглядеть раковина, которой не нашлось уголка в математическом здании? Ни рис. 6.12а показана такая улитка. Ее конусность не постоянна, а меняется по мере роста раковины. Более молодые, широкие части растут при меньших значениях конусности, чем узкие витки, образовавшиеся раньше. Поэтому у нее такой неестественный и, вероятно, непрочный шпиль на макушке. Это гипотетическая раковина. Ее можно увидеть только на экране монитора. У конической раковины с рис. 6.12b тоже необычная заостренная макушка. Это также произведение “Слепого строителя”, но здесь уменьшение конусности в процессе развития было запрограммировано.

На рис. 6.13 изображены настоящие раковины, и, я думаю, у них конусность тоже непостоянная; они зародились с относительно высокой конусностью, а по мере роста она неуклонно уменьшалась. Рауп считает, что параметры некоторых существовавших в древности аммонитов могли меняться в процессе роста раковин. Можно было бы предположить, что эти необычные раковины перемещаются из одной галереи в другую, пока растут, и до сих пор остаются в коллекции музея. Однако не менее верно и то, что нет такой витрины, где они могли бы храниться целиком, ибо организм молодой особи является частью взрослого организма. Насколько раковины с рис. 6.13 вписываются в трехмерное пространство нашего куба – это вопрос для дискуссии. Герат Вермей, один из ведущих современных специалистов по зоологии животных, имеющих раковины, полагает, что изменение параметров раковины по мере роста животного скорее норма, чем исключение. Иными словами, по его мнению, большинство моллюсков в течение жизни хотя бы немного перемещаются по математическому музею.

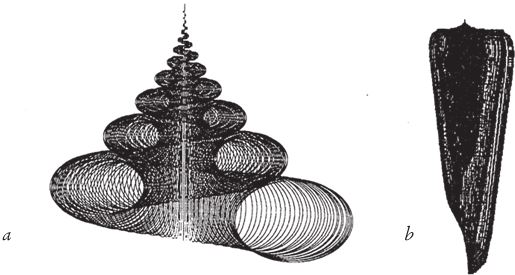
Рис. 6.12. Острые кончики компьютерных улитки (а) и конической раковины (b) сформировались под влиянием изменяющегося гена конусности.

Давайте рассмотрим обратную проблему – почему в большей части музейных залов не встречаются существующие в природе раковины. На рис. 6.14 показаны созданные компьютером раковины из глухих, “мертвых” зон музея. Они неплохо смотрелись бы на голове антилопы или бизона, но моллюск отказался бы от подобного домика. Почему таких раковин не бывает? Этот вопрос возвращает нас к тому противоречию, с которого мы начали. Не хватает вариантов изменчивости, и это накладывает ограничения на эволюцию, или естественный отбор принципиально против каких‐то отделов музея? Сам Рауп описал пустующие (незакрашенные) залы своего кубика с точки зрения селекции. Животные, имеющие раковину, не испытывают влияния давления отбора, которое могло бы направить их в свободные зоны. Можно сказать по‐другому: эти теоретически возможные формы нежизнеспособны – такие раковины были бы слабыми, хрупкими или подверженными угрозам другого характера; а может, их строительство обошлось бы слишком дорого из‐за расхода материала.

Другие биологи считают, что никогда не случалось тех мутаций, которые бы позволили попасть в эти области пространства. Это можно сформулировать иначе: мы нарисовали хранилище вроде бы для всех раковин, но на самом деле оно не полностью соответствует занятому ими пространству. Согласно этой идее, многих залов, даже с благоприятными для выживания вариантами раковин, не должно было появиться. Лично я склоняюсь к селекционистской трактовке Раупа, однако в данный момент не хочу ни на кого давить: я обратился к теме раковин лишь затем, чтобы пояснить смысл математики вероятных видов.

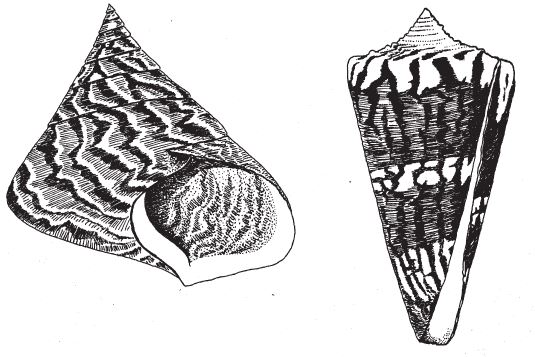
Рис. 6.13. Сходство форм этих природных раковин с компьютерными, показанными на рис. 6.12, заставляет предположить, что и они развивались при переменной конусности. Слева: каллиостома Maurea tigris, справа: улитка конус Conus generalis.

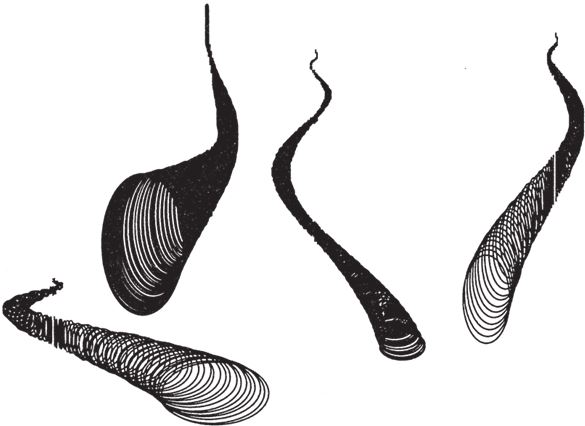
Рис. 6.14. Эти раковины придуманы, такая форма возможна разве что для рогов антилопы.

Не могу покинуть “запретные” залы, хотя бы вкратце не рассказав о некоторых причудливых, но тем не менее ныне живущих видах. Маленький морской головоногий моллюск Spirula (к этой же группе принадлежат кальмары и аммониты) – родственник наутилуса. Неплотная раковина с большими интервалами между витками указывает на высокое значение червячности (больше 1/расширение) – это ее качество уже было проиллюстрировано на рис. 6.4. Spirula могла бы послужить ярким примером, подтверждающим гипотезу о том, что раковины с большой червячностью – хрупкие и потому не выживают. Моллюску она служит не жилищем, а как бы внутренним плавательным пузырем. Поскольку эта раковина не несет защитных функций, природа позволила ей следовать по такому эволюционному пути, который ведет в непопулярные залы Музея Всех Возможных Раковин. Но все‐таки она занимает свою нишу. То же относится и к виду Vermicularia spirata (рис. 6.15). Вермикулярия обитает в Карибском море, а образом жизни и формой напоминает кольчатого червя. Во всяком случае, если вы спуститесь в правый нижний угол рис. 6.8, то попадете примерно в тот сектор музея, где хранится эта раковина. При этом ее близким родственникам – равно как и некоторым вымершим аммонитам, – не таким стройным и красивым, не нашлось подходящего местечка.

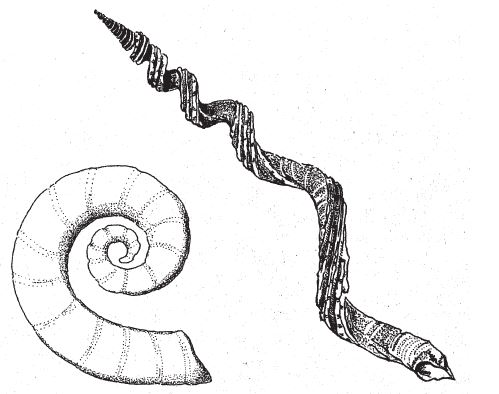
Рис. 6.15. Настоящим раковинам из малонаселенных отделов музея не так-то просто выживать в природе. Spirula spirula и встречающаяся в Карибском море Vermicularia spirata.

В нашем трехмерном музее игнорируется не только тот факт, что не все раковины круглые в сечении. Не учитываются также рельеф и окраска – тигровые и леопардовые узоры (рис. 6.10), каллиграфические шевроны (рис. 6.4а), бороздки и каннелюры всех разновидностей, которые так украшают раковины. Можно включить в программу нужные команды и внедрить в модель некоторые рисунки – например, по такой схеме: по мере образования новых витков расширяющаяся труба нарастает кольцами, причем каждое n-ное кольцо толще остальных. По этому алгоритму в зависимости от значения n на отдельных участках поверхности раковины появятся вертикальные полосы. Можно придумать более сложные алгоритмы для вычурных узоров. Немецкий ученый Ханс Майнхардт проанализировал такие алгоритмы. На рис. 6.16 вверху показаны рисунки раковин двух моллюсков – представителей оливид (сем. Olividae) и волютид (сем. Volutidae). Под ними – почти точные их копии, нарисованные в программе Майнхардта. Как вы можете убедиться, его алгоритм работает примерно так же, как биоморфное “дерево” – с той разницей, что результатом является не ветвление, а периодическая смена окрашенных и неокрашенных графических элементов. Подробнее об этом можно прочитать в его книге “Законы красоты морских раковин” (The Algorithmic Beauty of Sea Shells), но я вынужден оставить эту тему и вернуться к нашей основной, то есть в Музей Всех Возможных Раковин.

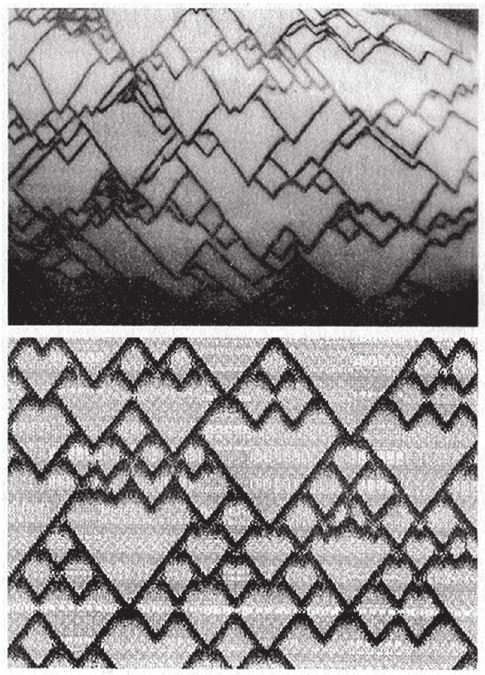
Рис. 6.16. Рисунки живых раковин и их компьютерные модели.

Концепцию музея я предложил по одной-единственной причине – если не усложнять картину и не учитывать сечение трубы, узоры и переменные параметры, то большинство известных раковин более или менее хорошо поддается количественному описанию тремя включенными в алгоритм рисования числами. Если мы захотим описать не раковину, а какое‐нибудь животное, нам придется выдумать музей, в котором будет больше координат, чем мы сможем отобразить. Пусть визуализация многомерного Музея Всех Возможных Животных – задача неподъемная, но есть некоторые связанные с ним простые идеи, которые легко укладываются в голове. Во-первых, животным свойственно располагаться рядом с теми животными, на которых они больше всего похожи, и, во‐вторых, по галереям музея можно перемещаться в любом направлении, а не только прямо, вдоль коридоров. Эволюционная история представляет собой траекторию, петляющую по некоторым частям музея. Поскольку в каждой филогенетической группе необыкновенно разнообразных царств животных и растений эволюция идет независимо, можно проследить тысячи таких траекторий, пронизывающих в разных направлениях разные отделы гигантского многомерного музея; обратите внимание, как далеко мы отошли от горы Невероятности, совершенно другой метафоры.

Теперь мы можем по‐новому интерпретировать суть нашего старого спора. В представлении одних биологов вы ходите по длинным галереям музея и по всем направлениям замечаете плавные градиенты постепенного изменения признаков. На самом деле во многих залах никогда не было живой материи, однако, по законам этой теории, она могла бы там появиться, если бы только естественному отбору было угодно повернуть в ту сторону. Другая группа биологов (я скорее не на их стороне, хотя, возможно, они и правы) полагает, что естественному отбору навсегда заказан вход в очень многие музейные залы и что ему так и не удалось прорваться в некоторые галереи, поскольку не случилось необходимых мутаций. И напротив, если творчески развить эту идею, – некая сила затягивала животных в другие, незапертые, залы, словно магнит или воронка, почти без вмешательства усердно работавшего естественного отбора. При таком взгляде на ход вещей Музей Возможных Форм Животных – это не правильно распланированное здание с длинными коридорами и плавной сменой экспозиций, а набор изолированных магнитов, каждый из которых усыпан торчащими железными опилками. Железные опилки символизируют животных, а пустующие пространства между магнитами – промежуточные формы, которые вообще‐то не могли бы существовать, но если бы появились, может, и выжили бы. Это можно сформулировать иначе, даже лучше: мы неправильно трактуем понятия “промежуточная форма” и “сосед” в мире животных. Истинно соседствующими следует считать формы, разделенные одной мутацией. Внешне они не всегда выглядят как соседи.

Хотя у меня и есть свое мнение в этой дискуссии, я стараюсь соблюдать объективность. Но в одном я убежден – если в природе мы видим что‐то, что можно счесть хорошо спроектированным для выполнения определенной задачи, за этим “чем‐то” стоит только естественный отбор. Я не настаиваю на том, что естественный отбор способен отомкнуть замки во всех залах и галереях Музея Всех Возможных Животных, и вовсе не считаю, что из любого закутка музея можно попасть в любой другой. Очень вероятно, что далеко не все пути открыты естественному отбору. Может статься, правы те мои коллеги, которые полагают, что естественный отбор далеко не всюду может пробраться или хотя бы проскочить. Но если инженер удивится тому, как здорово тот или иной орган приспособлен для выполнения определенной задачи, тут я встану и решительно заявлю, что автор гениальной “конструкции” – естественный отбор. Без его помощи никакие “магниты” или “аттракторы” в пространстве форм животных не обеспечили бы хороший функциональный дизайн. Однако позвольте мне немного ослабить накал страстей и познакомить вас с теорией “калейдоскопической” эмбриологии.