И статистика бывает интересной

Люди, которые объединены в группы, представляют собой сложную самоорганизующуюся систему. А в таких системах между элементами существует взаимозависимость. Она существует даже тогда, когда мы о ней не догадываемся. Это факт. Это не означает, однако, что любая ваша активность, ваше настроение или мысль мгновенно распространяются на всю группу. Нет, конечно. Сначала система должна достичь точки критичности. Или, как говорят физики, должна накопиться критическая масса. И тогда любое ваше действие станет тем самым поводом, который изменит всю систему.

Очень важно понимать, что не все системы, состоящие из множества элементов, обладают свойством самоорганизации. Существуют системы, в которых взаимозависимость между элементами отсутствует. Как же тогда отличить ситуации присутствия и отсутствия взаимозависимости? Оказывается, это как раз тот случай, когда математика помогает легко и элегантно решить проблему. А если точнее, то не математика в целом, а один из ее разделов, который носит название «статистика».

Спросите любого, кто прослушал в вузе курс статистики, помнит ли он хоть что-нибудь и пригодилась ли она ему в дальнейшем. Скорее всего, 99 из 100 сморщатся при одном лишь упоминании слова «статистика». Сразу же вспоминаются какие-то условные вероятности, распределения, логарифмы, экспоненты и всякие там дисперсии. У многих сложилось впечатление (и, кстати, небезосновательно), что университетская статистика – это почти всегда скучно, сложно и, самое главное, абсолютно бесполезно.

Как преподаватель с большим стажем и опытом работы с ох какой разной аудиторией ответственно заявляю: и статистике можно обучать так, чтобы вызывать неподдельный интерес и внимание у студентов. Даже у самых нерадивых! Давайте попробуем.

Каждый из нас вольно или невольно стремится обуздать неопределенность, исключить случайность из жизни, все заранее спланировать и предусмотреть. Если окружающий мир кажется нам предсказуемым и закономерным (ключевое слово здесь – кажется), мы чувствуем себя комфортно и уверенно. Если мы видим и понимаем причинно-следственные связи между явлениями, мы с легкостью принимаем решения, осуществляем планирование, делаем оценки и сравнения.

Однако далеко не всегда нам удается исключить случайность и понизить степень неопределенности (я, например, уверен, что никогда, однако, не буду навязывать вам свою точку зрения). И тогда мы обращаемся к царице всех наук – математике. А точнее, к ее большой и сложной области, которая называется теорией вероятностей. Теория вероятностей – это всего-навсего наука о… случае. Вот как ее охарактеризовал великий Пьер-Симон Лаплас еще в 1776 году:

…существуют вещи, которые для нас неопределенны, вещи, более или менее вероятные, и мы стараемся компенсировать возможность их узнать, определяя различные степени достоверности. Получается, что слабости человеческого разума мы обязаны появлением одной из самых тонких и искусных математических теорий – науки о случае, или о вероятности.

Просто, понятно и… элегантно, не правда ли? Ну конечно, ведь это великий Лаплас!

Именно теория вероятностей помогает найти закономерности там, где они не очевидны (математики называют это регрессией). Если мы имеем дело с совершенно случайными процессами – такими, как, например, погодные явления, результат подбрасывания монеты, показатель человеческого роста и попадание в цель снарядов, выпущенных из пушки, именно теория вероятностей успокаивает наш встревоженный разум, нашептывая нам примерно следующее: «Ничего страшного, мой любознательный друг, мир по-прежнему познаваем, и пусть ты не в состоянии сделать точный прогноз следующего подбрасывания монеты, но зато ты заранее знаешь распределение орлов и решек при большом количестве подбрасываний!»

Давайте осуществим небольшой экскурс в теорию вероятностей (кто-то сейчас опять вздрогнул). Обещаю – без сложных формул и определений.

Итак, поставим следующий мысленный эксперимент. Мы будем стрелять из пушки в цель, расположенную на расстоянии 500 метров. Пушка – вполне настоящая, не математическая. Это означает, что мы не всегда будем попадать в цель – некоторые ядра будут падать за пределами цели, другие – не долетать. Но не будем недооценивать наши способности пушкарей, большинство снарядов все же упадет именно туда, куда мы целимся.

Предположим, что, для начала хорошенько пристрелявшись и настроив все механизмы пушки, мы сделали 100 выстрелов. Теперь давайте подсчитаем точность наших попаданий. Пушкарь, сама пушка и вылетевшие из нее ядра представляют из себя простую систему. В контексте данной главы это означает, что каждый выстрел никак не влияет на последующий и не зависит от предыдущего. Итак, подавляющее большинство ядер упало именно в цель, то есть на 500 метров. Некоторые ядра улетели чуть дальше цели, сколько-то снарядов не долетело. Чем дальше от цели (в ту и в другую сторону), тем меньше ядер туда упало. Если мы нарисуем график зависимости числа ядер (в штуках) от точности выстрела (в метрах), то он будет выглядеть примерно так:

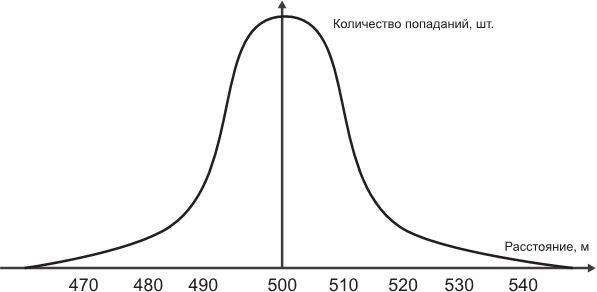
Результат 100 выстрелов из пушки на расстояние 500 метров

Эту кривую математики называют «график нормального распределения случайной величины». Случайная величина в данном случае – это падение пушечного ядра в ту или иную точку. Как бы мы ни целились, полет ядра действительно во многом случаен. Случайность объясняется огромным количеством факторов, которые влияют на ядро и которые учесть просто невозможно – химические свойства пороха, сила ветра, сила притяжения Земли, сила притяжения Луны, сила притяжения Солнца, настроение пушкаря, сердцебиение пушкаря, проплывающее мимо облако, температура воздуха, невидимые искажения формы ядра и пр. Если бы всего этого бесконечного множества факторов не существовало, то каждое вылетевшее из пушки ядро попадало бы точно в цель, но так как их влияние исключить нельзя, то говорят, что в какой-то степени полет ядра носит случайный характер.

График нормального распределения любой случайной величины (в нашем случае это попадание ядра) носит и другое название – «кривая Гаусса», в честь немецкого математика Иоганна Карла Фридриха Гаусса (1777–1855).

Иоганн Гаусс – великий ученый всех времен и народов. За выдающиеся заслуги его иногда называют «королем математики», хотя он достиг успехов и в других областях науки – в механике, физике, геодезии и даже в астрономии. Он был членом многих академий, в том числе и Российской.

Гениальные способности к математике проявились у Гаусса в раннем детстве. Уже в три года он не только умел считать и писать, но даже помогал отцу производить сложные арифметические вычисления.

Уже будучи известным ученым, Гаусс решил выучить русский язык, чтобы в оригинале познакомиться с трудами великого русского ученого Лобачевского. Этот поступок заслуживает восхищения, не правда ли?

Карл Фридрих Гаусс (1777–1855). Немецкий математик, механик, физик, астроном и геодезист. В честь него названа знаменитая «гауссиана» – кривая, описывающая нормальное распределение случайных событий

Гаусс прожил долгую и насыщенную жизнь, хотя, как и сэр Ньютон, из скромности не опубликовал множества своих открытий, мыслей и расчетов. О значимости этого ученого свидетельствует тот факт, что его портрет, а также изобретенный им измерительный инструмент были изображены на денежной купюре (номиналом 10 марок) – очень немногие заслуженные и незаурядные личности удостоились столь высокой чести.

Гауссов закон нормального распределения представляется одним из самых существенных вкладов этого великого ученого в науку. Отдавая долг исторической справедливости, необходимо отметить, что сам закон был открыт не Гауссом, однако именно немецкий математик детально и глубоко его изучил и дополнил. Иногда закон нормального распределения называют законом Гаусса – Лапласа, признавая тем самым вклад в развитие теории вероятностей другого, ранее нами уже упоминавшегося великого ученого французского происхождения.