Нормальное распределение случайных событий

Но вернемся к нашей пушке. Зачем нам нужен график распределения попаданий ядер в цель, что он дает и для чего вообще нужно рассчитывать, сколько ядер и куда упало? А вот для чего: определив функцию зависимости количества попаданий от общего количества выпущенных ядер, мы получаем в пользование весьма эффективный инструмент для прогнозирования. Теперь, если кто-то другой будет стрелять из этой же пушки, мы уже заранее сможем предсказать, сколько ядер и куда попадет: столько-то в цель, у стольких-то будет недолет 10, 20 и т. д. метров, у стольких-то перелет на 10, 20 и т. д. метров. А также, что не менее важно, мы сможем заранее рассчитать вероятность попадания каждого конкретного ядра в цель! Хороший математический инструмент, не правда ли? Теперь мы можем прогнозировать. И с использованием графика распределения Гаусса наши прогнозы будут весьма точны.

Но это еще не всё. Пожалуй, самое главное знание, которое дает нам график распределения Гаусса, это разброс попаданий. Чтобы понять, что это такое и зачем это нужно, стоит набраться терпения.

Представьте, что вы собираетесь провести свой отпуск в некой экзотической стране. Подготовка к путешествию требует изучения и анализа многих фактов о будущем месте пребывания, начиная с курса местной валюты и заканчивая меню в ресторанах. Крайне важно также знать особенности климата и температурного режима в этой стране. Допустим, наш верный друг и помощник википедия подсказывает, что среднегодовая температура в этой экзотической стране составляет плюс 25 градусов по шкале Цельсия. Отлично, думаете вы, достаточно комфортная температура – не зажарюсь, но и не замерзну. Но будете ли вы полностью удовлетворены этим ответом? Конечно же, нет! Информация о значении средней температуры имеет невысокую ценность. Ведь вы так и не узнали, какую одежду вам стоит взять с собой в путешествие. Средние 25 градусов могут означать многое. Например, незначительные колебания температуры в течение года от 23 до 27 градусов, что вполне комфортно и безопасно. Но 25 градусов в среднем могут означать и совсем другие погодные условия: например, колебания температуры в течение года от минус 10 до плюс 40 градусов. Или даже от минус 30 (но в течение короткого периода времени) до плюс 27 (в течение большей части года). Представляете, если вы не угадали с фазой температурного цикла и захватили с собой легкую майку и шорты вместо дубленки на овечьей шерсти и меховой шапки?

Таким образом, само понятие среднего вовсе не информативно, ибо важен разброс показателя. Вот тут-то на помощь и приходит такая характеристика, как «стандартное отклонение от средней арифметической», или «среднеквадратическое отклонение». Не удивлюсь, если на этом месте у многих читателей возникли неприятные ассоциации со студенческим курсом статистики. На самом деле среднеквадратическое отклонение не такая уж сложная штука. Давайте рассчитаем этот показатель для пяти выстрелов из нашей пушки.

Предположим, наше искусство пушкаря можно описать следующим образом:

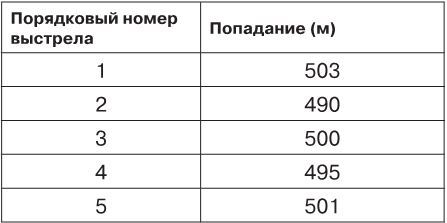
Ну что ж, неплохо, мы стреляем довольно-таки кучно. Один из выстрелов (номер 3) попал точно в цель. Остальные выстрелы отклонились от цели (она же – среднее значение) совсем ненамного:

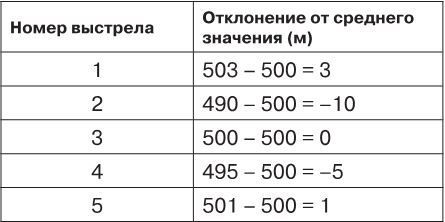
Теперь осталось найти среднее значение из вычисленных нами отклонений. Статистики обычно говорят тут запутанную фразу – необходимо найти среднее значение из отклонений от среднего. Итак, нам надо сложить полученные отклонения (3+ (-10) + 0 + (-5) +1) и разделить на количество выстрелов (5). Обычное среднее арифметическое, ничего сложного.

Тут, правда, возникает одна проблема – в математической формуле перелеты и недолеты взаимоуничтожают друг друга, например, перелет на 3 метра и недолет на 10 метров в сумме дадут недолет на 7 метров. Поэтому нам надо избавиться от знака «минус» в полученных отклонениях. Для этого возведем все значения из предыдущей таблицы отклонений в квадрат (как известно, квадрат отрицательного числа есть число положительное).

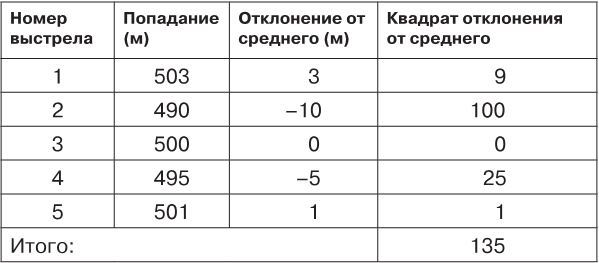
Итак, теперь осталось разделить полученное значение на количество выстрелов:

135:5=27.

И, под конец, извлечь корень квадратный из полученного числа, чтобы восстановить справедливость (нарушенную, когда мы возвели в квадрат значения отклонений попаданий).

Что мы получаем? Стандартное отклонение пяти выстрелов от среднего значения (500 метров) равно 5,2. Теперь переведем это на русский язык:

стреляя из пушки, мы попадаем в цель, расположенную на расстоянии 500 метров, со стандартным отклонением плюс-минус 5,2 метра.

Вот это уже другое дело, теперь у нас в руках есть весьма эффективный математический инструмент для определения меткости стрелка. Ведь одно дело, когда разброс равен 5,2 метра, и совсем другое, когда стрелок попадает в цель, расположенную в 500 метрах, с отклонением плюс-минус 50 метров.

Правило трех сигм

В науке показатель среднеквадратического отклонения для краткости называют латинской буквой σ (сигма). То есть мы можем сказать, что сигма наших выстрелов равна 5,2 метра. А есть ли снаряды, которые улетели (или не долетели) от цели больше чем на 5,2 метра (то есть больше, чем на одну сигму)? Конечно, есть, но их немного. А есть ли те, которые улетели (не долетели) еще дальше, например на 15,6 метра (больше трех сигм)? Есть, но их окажется совсем-совсем мало. То есть чем дальше от цели, тем меньшее количество снарядов туда полетит (не долетит). И, зная разброс попаданий, мы даже можем сказать, сколько именно!

Давайте отложим на горизонтальной линии отрезки, равные одной, двум и трем значениям сигм. В обе стороны от среднего, то есть от 500 метров:

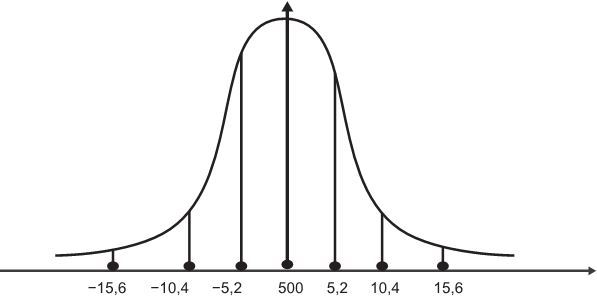
Большинство выстрелов из пушки попало точно в цель, плюс-минус три среднеквадратических отклонения

Что мы можем сказать про количество снарядов, которые попадут в диапазон плюс-минус одна сигма, плюс-минус две сигмы и плюс-минус три сигмы? Оказывается, статистика дает нам ответ и на этот вопрос (при условии, что распределение попаданий действительно описывается нормальным законом)!

68,2 % всех попаданий приходится на диапазон 500 метров плюс-минус одна сигма.

95,4 % всех ядер окажется в диапазоне 500 метров плюс-минус две сигмы.

99,7 всех попаданий не выйдет из диапазона 500 метров плюс-минус 3 сигмы.

Удивительная штука! Получается, что почти 100 % всех ядер, которые вылетят из нашей пушки, попадут в цель плюс-минус 15,6 метра (три сигмы).

Внимание! Очень важное пояснение: эти закономерности действительны не только для вышеописанного случая, они действительны для всех-всех пушкарей! Просто у каждого пушкаря будет своя сигма. Все зависит от его квалификации. У нас она равна 5,2 метра. У кого-то еще, например, 7,4 метра. То есть для этого, менее искусного, чем мы, пушкаря действует тот же закон, что и для нас, просто значение сигмы у него будет другое.

В теории вероятностей эта закономерность называется «правилом трех сигм». С его помощью мы можем оценить квалификацию нашего пушкаря. И не только его. Помните пример про отпуск и среднегодовую температуру? Теперь, обладая информацией о распределении температур в этой экзотической стране, вы точно знаете, какую одежду с собой брать. А представьте, что вы решили доверить свои сбережения опытному трейдеру. Опросив с десяток специалистов, вы остановились в итоге на двух. Оба обещают годовую доходность в районе 20 %. Только у первого три среднеквадратических отклонения равны 5 %, а у второго – 25 %. Теперь вы знаете, что в 99,7 года из ста первый трейдер заработает для вас 20 % плюс-минус 5 %. Второй же может заработать больше – до 45 %, однако и проиграть он может тоже больше, вплоть до минус 5 % годовых. Думайте, выбирайте.

Вернемся к нашей пушке. Ну а может ли ядро улететь на 26 метров (что соответствует пяти сигмам в нашем примере)? Да, это возможно, но подобная вероятность крайне, просто ничтожно мала. Если, всласть настрелявшись, вы будете уверять меня, что все же умудрились так далеко послать ядро (или, наоборот, допустить недолет), я могу сделать следующий вывод: скорее всего, вы мошенник. Ведь вероятность, что вы случайно допустили такой промах при прочих равных условиях, равна одному из миллиона! Или, другими словами, здесь что-то не так. Или порох отсырел, или прицел сбился, ну или вы преднамеренно или случайно ошиблись в расчете точки попадания ядра. Одним словом, скорее всего, это не был случайный промах. Вот так, вооружившись «правилом трех сигм», можно делать оценки и давать характеристики (правда или неправда) в отношении редких событий, что активно используют в своей работе, например, следователи, риск-менеджеры, финансисты (это же правило нередко является причиной фатальных ошибок, но об этом позже).

А как насчет перелета или недолета на 10 сигм? То есть можно ли, целясь на 500 метров из той же самой пушки и при всех тех же самых условиях промахнуться аж на 52 метра? Ответ однозначный – нет! На языке статистики это правило звучит так:

При нормальном законе распределения случайной величины отклонение, равное пяти сигмам, встречается очень редко (теперь вы уже знаете – один случай на миллион), а отклонение в 10 сигм не встречается НИКОГДА!

Итак, у нас в руках есть очень эффективный инструмент. Теперь, если кто-то задумает пострелять из пушки в цель на расстоянии 500 метров, мы можем заранее предсказать распределение попаданий. 99,7 % всех выстрелов попадет в цель плюс-минус три стандартных отклонения. При этом лишь в одном случае из миллиона выстрелов снаряд улетит или не долетит на величину 5 сигм. А вот недолет или перелет на 10 сигм наш стрелок не увидит никогда.