Задача о падении тела позволяет на достаточно простом примере продемонстрировать, как мы можем улучшать результаты с помощью расчетов на основе все более точных моделей. Мы последовательно рассмотрим три задачи: падение вблизи поверхности Земли в пренебрежении сопротивлением воздуха, падение с очень большой высоты, падение с учетом сопротивления среды.

Первый вариант задачи совсем школьный – движение с постоянным ускорением. Ускорение создается силой земного притяжения и равно:

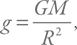
где G – гравитационная постоянная, а M и R – масса и радиус Земли. Тело падает с небольшой высоты h, которая намного меньше R, а потому изменением ускорения можно пренебречь.

Все необходимые формулы приведены в учебнике физики за 9-й класс. За время t скорость будет возрастать на величину gt. При нулевой начальной скорости за время t тело проходит расстояние, равное gt² / 2. Откуда берется такая формула, легко представить графически.

Нарисуем график зависимости скорости от времени для равноускоренного движения. Это будет прямая линия. Путь, пройденный за небольшой промежуток времени dt, равен произведению текущей скорости (за маленький интервал времени она не успевает существенно измениться) на dt. Эта величина равна площади вытянутого в вертикальном направлении прямоугольника на графике. Соответственно, весь пройденный путь складывается из суммы таких прямоугольников и, таким образом, равен площади фигуры под линией изменения скорости, представляющей собой треугольник. Его площадь можно вычислить: умножим половину длины стороны на высоту треугольника, опущенную к этой стороне. Сторона равна t, а высота – это конечная скорость, равная gt. Соответственно, время падения с высоты h равно квадратному корню из удвоенной высоты, разделенной на ускорение свободного падения: t = (2h / g)^{1 / 2}.

Теперь рассмотрим более сложный случай – падение с большой высоты, сравнимой с радиусом Земли. В такой постановке ускорение будет меняться, т. е. скорость будет расти все быстрее. Подобный эксперимент можно было бы поставить на Луне, где не мешает атмосфера.

Мы не будем решать задачу до конца путем интегрирования (хотя интеграл там табличный), но зато получим качественную зависимость времени падения от начального радиуса для случая, когда он намного больше радиуса планеты R. Очевидно, что чем дальше мы отходим от поверхности, тем меньше ускорение: a (r) = GM / r², где r = R + h.

Значит, если мы рассмотрим небольшой интервал времени dt, в течение которого смещение невелико и ускорение меняется слабо, то dr = v (r) dt + a (r) (dt)² / 2. Полное время падения с расстояния r будет в основном определяться медленным движением вдали от планеты: там и скорость еще мала, и ускорение невелико. Значит, верхним пределом на время падения будет величина, которую можно получить из уже записанной формулы t = (2h / g)^{1 / 2}. Заменим здесь высоту h на r, а ускорение g – на соответствующую величину a (r) = GM / r². В итоге мы получим, что при больших расстояниях от поверхности время падения растет как r^{3 / 2}.

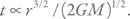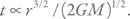Неплохой оценкой времени падения является отношение начального расстояния r к скорости свободного падения на этом расстоянии: v = (2GM / r)^{1 / 2}. Иными словами, Такую оценку часто применяют, например, для определения времени падения захваченного из межзвездной среды вещества на нейтронную звезду. Разумеется, точная величина будет несколько меньше, но по порядку величины это очень хорошая простая оценка.

Для случая, когда расстояние, с которого начинается падение, намного больше размера центрального тела, можно получить более точную оценку, воспользовавшись третьим законом Кеплера. Представьте себе две орбиты, касающиеся в одной точке. Одна – круговая с радиусом r. Вторая – крайне эксцентричная, практически «иголочка». В первом случае большая полуось равна r, а во втором – r / 2. Падение соответствует половине орбитального периода второй орбиты. Для первой легко посчитать орбитальный период:

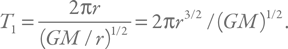
Период второй орбиты, в соответствии с третьим законом Кеплера, будет меньше в 2^{3 / 2} раза. Таким образом, время падения составит:

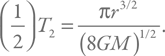
Теперь рассмотрим роль сопротивления воздуха. Все знают, что при падении с большой высоты (скажем, если кто-то выпал из самолета) скорость возрастает лишь до некоторого предела. Поэтому, кстати, все равно, с какой высоты падать – один или десять километров, все равно в момент удара скорость будет та же самая. Очевидно также, что объект большой площади наберет меньшую скорость, поэтому прыгать лучше с парашютом. Получим простую количественную оценку.

Итак, с какого-то момента тело перестанет увеличивать скорость, т. е. его ускорение будет равно нулю. Значит, сила тяжести уравновешена силой сопротивления среды. Напомним, что сила – это изменение импульса за данное время. Сила сопротивления складывается из ударов множества молекул. Значит, нам надо посчитать, какой импульс передадут молекулы за время t телу с площадью S.

Наше тело движется со скоростью v в среде с плотностью частиц n (эта величина показывает, сколько частиц содержится в единице объема, ее можно рассчитать. Разделим плотность среды на массу одной частицы, т. е. в нашем случае это примерно плотность воздуха ρ, деленная на массу молекулы азота N₂). Каждая молекула передает импульс, равный удвоенному произведению скорости тела на массу молекулы. Стало быть, нам надо узнать, сколько молекул сталкивается с телом за время t.

Сделать это легко. Надо лишь подсчитать объем, «заметаемый» телом при движении. Он равен произведению площади S на скорость и на время. Теперь этот объем умножаем на концентрацию молекул n. В итоге сила сопротивления равна:

где m₀ – масса молекулы.

Эта сила уравновешена силой тяжести, равной mg, где m – масса падающего тела, а g – ускорение свободного падения. Равенство двух сил позволяет вывести простую формулу для соответствующей скорости:

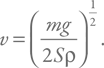
Зависимости прозрачны. Чем массивнее тело, тем быстрее оно будет падать. Чем больше плотность среды, тем меньше скорость. Большая площадь также позволяет уменьшить скорость падения (забыли парашют – распахните пальто).

Можно подставить какие-нибудь характерные значения и дать оценку скорости. Округляя, мы получим, что тело массой около 100 кг и площадью 1 кв. м может набрать скорость порядка 100 км/ч. Такая скорость набирается при падении с высоты метров 40. У человека площадь меньше, поэтому, с одной стороны, можно разогнаться до пары сотен км/ч, а с другой – получить оценку, что парашют с площадью порядка 100 кв. м должен замедлять спуск до безопасных скоростей.