Уже более 300 лет назад астрономы могли убедиться, что наблюдаемые небесные тела (планеты и их спутники) имеют округлую форму. Однако очевидно, что камень (в том числе и летающий в космосе) может иметь довольно причудливую форму. Легко сообразить, в чем дело: гравитация придает крупным телам сферическую форму, «сглаживая» неровности, как мы, создавая давление руками, лепим круглые снежки.

Можно ли примерно оценить размер тела, при котором оно уже не сможет поддерживать заметно несферическую форму? Оказывается, сделать это легко. Надо всего лишь знать закон всемирного тяготения.

Догадаться о структуре закона, определяющего гравитацию, тоже можно. Во-первых, сообразить, что чем массивнее тела, тем больше гравитационное взаимодействие между ними. Во-вторых, из-за трехмерности однородного и изотропного пространства сила будет спадать как квадрат расстояния. Получаем известный из школьной физики закон:

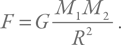
Здесь в числителе стоят массы притягивающихся тел. Нас будет интересовать ситуация, когда M₁ – масса планеты, M₂ – масса заметной неоднородности на ней (по сути, речь идет о горе на поверхности). А стоящая в знаменателе величина R – радиус планеты.

Теперь нам надо правильно сформулировать задачу на качественном уровне. Мы знаем, что самые высокие горы на Земле имеют высоту несколько километров. Давайте положим предельную высоту равной 10 км. Если гора будет более высокой, то породы в ее основании не выдержат давления, и гора осядет. Давление (обозначим его P) равняется частному от деления силы на площадь (обозначим ее S): P = F / S. Сделаем разумное предположение, что критическое давление будет одним и тем же для всех космических тел, интересующих нас. Запишем равенство критического давления в двух ситуациях:

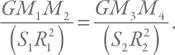
Слева – давление в основании горы массой M₂ на первой планете с массой M₁ и размером R₁, а справа – давление в основании горы массой M₄ на второй планете с массой M₃ и радиусом R₂.

Теперь, чтобы рассчитать силу, нам надо знать массу горы. Представим себе гору как конус. Его масса пропорциональна объему. Математика дает нам возможность рассчитать объем конуса. Он пропорционален произведению высоты (h) на площадь основания: Нам нужно получить давление, таким образом, площадь основания не войдет в ответ.

Масса планеты пропорциональна ее объему. Объем шара пропорционален кубу радиуса: Подставив это в формулу и сократив все, что можно сократить, мы получим простое соотношение:

Нас интересует случай, когда второе тело имеет заметно несферическую форму, т. е. высота горы на второй планете сопоставима с радиусом, т. е. R₂ = h₂. Соответственно, для оценки критического радиуса тела, которое может начинать заметно отклоняться от сферической формы, получаем:

Подставим в качестве R₁ радиус Земли, в качестве h₁ – предельную высоту гор на Земле и получим: R₂ ≈ 250 км.

Эта простая оценка прекрасно соответствует действительности: спутники и астероиды с диаметром менее нескольких сотен километров уже могут иметь заметно несферическую форму (примером может служить спутник Сатурна Прометей), а более крупные (как, например, Церера) – округлую. Разумеется, чем меньше размер, тем заметнее может быть отклонение от правильной формы. 500-километровые Веста и Паллада лишь слегка несферичны, а 100-километровая Лютеция уже сильно отклоняется от шарообразной формы.

Таким образом, воспользовавшись простыми геометрическими формулами (объем конуса, объем шара) и записав наши предположения о физике тела в математической форме, мы сумели в рамках простой модели рассчитать предельный размер тела, которое своей гравитацией может заметно сглаживать рельеф на своей поверхности. Конечно, можно проводить более детальные и точные расчеты, учитывая в первую очередь разницу во внутреннем строении различных тел (спутники и астероиды могут состоять из менее плотных пород, чем земная кора). Но прелесть именно в том, что уже без этих деталей можно получить вполне разумный результат.