Книга: Все формулы мира
Назад: Приложение 3 Аккреция, предельная светимость и массы сверхмассивных черных дыр
Дальше: Приложение 5 Астрофизика нейтронных звезд
Приложение 4
Одиночные черные дыры
Черные дыры, безусловно, являются крайне интригующими объектами, ускользающими не только от однозначной идентификации наблюдательными методами, но еще и от четкого определения. Тем не менее в астрофизике существует несколько методов, позволяющих регистрировать даже одиночные черные дыры звездных масс. Какие-то из них уже работают, какие-то – только на подходе. Ниже мы обсудим три ситуации: аккрецию вещества межзвездной среды, гравитационное микролинзирование и, наконец, испарение черных дыр (хотя этот процесс важен лишь для черных дыр малых масс).
4А. Аккрецирующие одиночные черные дыры
Ядра массивных звезд в завершение их эволюции могут превращаться в черные дыры. Точные интервалы начальных масс прародителей этих компактных объектов неизвестны, но для простой оценки предположим, что основная доля звезд, имеющих при рождении массы более 30 солнечных, в конце порождают именно черные дыры. Далее предположим, что распределение звезд по начальным массам можно описать так называемой солпитеровской функцией:
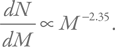
Это означает, что количество звезд dN в небольшом интервале масс шириной dM – от M до (M + dM) – пропорционально массе в степени –2,35, т. е. количество звезд быстро спадает с ростом массы. Данная зависимость была установлена на основе наблюдений.
В качестве минимальной массы звезды возьмем 0,1Mʘ, а в качестве максимальной – 100Mʘ. Теперь, чтобы посчитать долю звезд с массой более 30 солнечных, нам надо найти отношение двух интегралов:
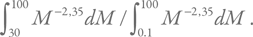
Это отношение примерно равно 0,00045. Учитывая, что за время существования Галактики в ней сформировалось около 300 млрд звезд, мы получим, что сейчас в ней должно быть около 135 млн черных дыр (заметим, что это очень близко к более точным расчетам). Типичная масса таких объектов – 5–10 масс Солнца. Это следует и из теории, и из наблюдения черных дыр в тесных аккрецирующих двойных системах.
При рождении черные дыры, в отличие от нейтронных звезд, в среднем не получают большую дополнительную скорость, связанную с асимметрией взрыва сверхновой (так называемый кик). Значит, они остаются в галактическом диске, и мы можем легко оценить их плотность в солнечной окрестности. Представим диск Галактики в виде цилиндра с радиусом около 15 кпк и толщиной около 1 кпк. Разделив его объем на количество черных дыр, получим объем, приходящийся на один объект, – это около 5000 кубических парсек. Значит, расстояние до ближайшей одиночной черной дыры будет порядка 10 пк.
Таким образом, черных дыр звездных масс в Галактике много, и они могут находиться не так уж далеко от нас. Вопрос в том, как их обнаружить.
В приложении 3 мы обсудили, что аккреция на черные дыры может приводить к выделению значительной энергии. Надо только найти эффективный источник вещества. Если компактный объект одиночный, т. е. бороздит просторы Галактики сам по себе, тогда единственным источником будет межзвездная среда.
Плотность межзвездного вещества вблизи плоскости диска Галактики в солнечных окрестностях не слишком высока – около одного атома водорода в кубическом сантиметре. В молекулярных облаках это значение возрастает в десятки, а то и в сотни раз. Нам нужно оценить, с каким темпом черная дыра может захватывать это вещество.
Чаще всего, когда на популярной лекции заходит речь о черных дырах, выясняется, что хотя бы кто-то из слушателей полагает, что черные дыры – это такие пылесосы, которые «затягивают в себя все и когда- нибудь совсем все и затянут». Это совсем не так.
Действие черных дыр на другие тела определяется гравитацией. Если мимо черной дыры пролетает тело, то нам надо сравнить его кинетическую энергию, связанную с движением относительно компактного объекта, и гравитационную потенциальную энергию, связанную с взаимодействием между телами. Формулу для кинетической энергии все помнят:
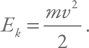
Потенциальную энергию удобно считать отрицательной, и для нее выражение выглядит так:

где G – гравитационная (ньютоновская) постоянная, M – масса массивного центрального тела (в нашем случае – черной дыры), m – масса пролетающего тела, а v – его скорость.
Ясно, что если скорость слишком велика, то кинетическая энергия тоже будет велика, и, таким образом, полная энергия, равная сумме кинетической и потенциальной, будет больше нуля, т. е. система будет гравитационно несвязанной. Иными словами, тело пролетит мимо. Точно так же при большом расстоянии между телами – r – потенциальная энергия будет мала, и снова связанная система не образуется. Таким образом, чтобы черная дыра захватила пролетающее тело (им может быть и молекула газа межзвездной среды), надо, чтобы выполнялось некоторое условие. Вот оно:
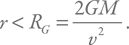
Критическое расстояние RG называют радиусом гравитационного захвата.
Однако мало тело захватить, ведь оно может просто вращаться вокруг черной дыры на устойчивой орбите (как Земля вокруг Солнца или Луна вокруг Земли). Телу нужно избавиться от вращения – потерять орбитальный момент. В системе двух тел такой возможности практически нет (исключение составляют приливы, а в случае черной дыры и атома водорода какие уж тут приливы!). Необходимо, чтобы вокруг центрального массивного объекта вращалось несколько тел, которые могли бы достаточно эффективно обмениваться энергией и орбитальным моментом. Тогда часть из них сможет перейти на более низкие орбиты и в конечном счете выпасть на центральный объект.
В случае аккреции вещества межзвездной среды захватывается газ, поэтому за счет вязкости можно обеспечить довольно эффективный отвод орбитального момента наружу. Взаимодействие частиц газа в потоке будет приводить к переносу орбитального момента прочь от гравитирующего центра, а вещество, потерявшее момент, будет течь в его сторону. Поэтому аккреция начинается, если вещество проникло под радиус гравитационного захвата. Теперь мы можем сделать простую оценку максимального темпа аккреции.
Итак, черная дыра массы M летит со скоростью v сквозь межзвездную среду плотностью ρ. Будем считать, что все вещество, попадающее внутрь радиуса гравитационного захвата, в итоге поглотится черной дырой. Значит, объем поглощенного за единицу времени вещества будет равен объему цилиндра, длина которого равна произведению скорости на интервал времени (не забываем, что он у нас единичный), а площадь основания равна  Таким образом, темп аккреции будет равен:
Таким образом, темп аккреции будет равен:
 Таким образом, темп аккреции будет равен:
Таким образом, темп аккреции будет равен:
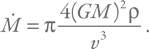
Учет некоторых тонкостей может изменить численный коэффициент, но общие зависимости останутся, и по порядку величины эта оценка верна.
Необходимо сделать один комментарий относительно скорости. Глядя на формулу, кажется, что можно достичь очень высокого темпа аккреции, если черная дыра будет двигаться относительно среды с очень низкой скоростью. Однако необходимо учесть, что частицы среды сами движутся, и в космических условиях эта скорость может быть довольно велика. Хорошей оценкой характерной скорости будет величина скорости звука vs в межзвездной среде, которая в зависимости от комбинации температуры и плотности может составлять от нескольких сотен метров в секунду в самых холодных и плотных областях до десятков километров в секунду. С учетом скорости звука формула немного изменится:
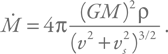
Если мы подставим в формулу типичные значения: ρ = 10–24 г / см3, M = 2·1034 г, а для обеих скоростей возьмем значения 10 км/с (в случае скорости звука это типичное значение, а вот для скорости движения – скорее, нижний предел), то получим примерно 1013 грамм в секунду.
Теперь возникает более сложный момент – посчитать эффективность аккреции, т. е. сколько энергии выделится на грамм вещества, провалившегося в конце концов в черную дыру. И вот тут ясности нет. Дело в том, что поверхность-то у черной дыры отсутствует! Иначе говоря, выделить энергию при контакте с поверхностью невозможно. Значит, все энерговыделение должно идти в потоке. Насколько оно эффективно, в ряде случаев неясно. Если аккрецируемое вещество обладает достаточно большим орбитальным моментом, то вокруг черной дыры формируется аккреционный диск. За счет вязкости (по сути, за счет трения слоев газа друг о друга) энерговыделение достигает больших значений. Именно поэтому мы видим мощное излучение квазаров, блазаров и других активных галактических ядер, а также черных дыр в рентгеновских тесных двойных системах. В том случае, если и при аккреции из межзвездной среды формируется диск, можно рассчитывать на довольно значительную светимость. Давайте попробуем оценить верхний предел для нее.
Поступим очень просто. Оценим гравитационную потенциальную энергию на внутреннем крае аккреционного диска. В случае черных дыр существует важное понятие последней устойчивой круговой орбиты. Для невращающейся вокруг своей оси черной дыры (а мы думаем, что одиночные черные дыры, блуждающие по Галактике, в основном имеют относительно медленное вращение, поскольку раскрутить черную дыру можно в первую очередь мощной аккрецией в тесной двойной системе) радиус такой орбиты равен 6GM/c2, т. е. трем шварцшильдовским радиусам. После достижения этой границы вещество в диске очень быстро «вспираливается» под горизонт. Таким образом, плотность вещества в потоке под критическим радиусом мала, а потому там трудно сгенерировать мощное излучение за счет вязкости. На радиусе гравитационного захвата вещество имеет практически нулевую энергию. Значит, верхний предел на энерговыделение будет примерно равен по модулю потенциальной энергии на последней устойчивой орбите. Воспользовавшись приведенной несколько выше формулой для массы m, получим энерговыделение (mc2 / 6). Это много: каждый грамм будет давать 1,5·1020 эрг. Объединив это с полученной выше оценкой темпа аккреции и немного округлив, получим примерно треть светимости Солнца – довольно заметный источник!
Однако до сих пор одиночные аккрецирующие черные дыры не идентифицированы (здесь я нарочито избегаю слов «не обнаружены», поскольку потом может оказаться, что какие-то из известных слабых источников относятся к данному классу объектов). Расчеты показывают, что в спектре излучения одиночных аккрецирующих черных дыр может быть два максимума: в инфракрасной и рентгеновской области. Соответственно, предпринимались попытки выявить слабые источники с такими свойствами. Проводились специальные поиски в направлениях молекулярных облаков, где выше плотность среды, а значит, выше темп аккреции и, следовательно, светимость. Но все пока безрезультатно.
Вероятнее всего, приведенная выше оценка темпа аккреции завышает реальную величину, а значит, черные дыры будут более слабыми источниками. Однако нет никаких сомнений, что в Галактике блуждают многие десятки миллионов черных дыр звездных масс, потихоньку поглощающих вещество межзвездной среды. При этом выделяется какое-то количество энергии в виде электромагнитного излучения. Стало быть, рано или поздно они будут обнаружены.
А пока есть другой, уже работающий способ открывать одиночные черные дыры.
4Б. Линзирование
Любое тело обладает массой, а значит, искривляет пространство-время вокруг себя. Это сказывается на движении всех объектов в данной области. Разумеется, чем массивнее тело, тем на большем расстоянии оно может оказывать заметное влияние. Нас будет интересовать, как присутствие массивного тела сказывается на распространении электромагнитных волн, и в частности света.
Заметим, что отклонение световых лучей как таковое – это не совсем «изобретение» общей теории относительности. Согласно ньютоновской модели, свет, если представить его себе как поток очень легких частиц (именно так себе представлял свет сам Ньютон), также должен отклоняться, только эффект будет в два раза меньше, чем в ОТО. Наблюдения смещения положения звезд во время солнечных затмений (а затем и другие многочисленные наблюдения и эксперименты) показали, что верен расчет в рамках ОТО – при небольших углах отклонения работает формула
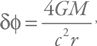
где δφ – угол, на который отклоняется свет, М – масса гравитационной линзы, а r – минимальное расстояние между траекторией светового луча и центром линзы.
Гравитационное линзирование встречается в астрономии в самых разных вариантах. В роли источника может выступать далекий квазар, а в роли гравитационной линзы – массивная галактика. Или же источником является далекая сверхновая, и ее свет линзируется на скоплении галактик. Мой любимый пример таков. Источником является аккреционный диск в далекой активной галактике, а его излучение линзируется на отдельных звездах более близкой галактики на луче зрения. В такой поразительной ситуации мы можем измерить параметры диска (по сути, определить, как его температура меняется с радиусом).
Однако здесь нас будет интересовать случай так называемого микролинзирования. Микро-, потому что линза относительно легкая, это объект звездной массы. Источником в такой ситуации обычно является звезда нашей Галактики, и, конечно, в ней же находится и линза.
Если мы смотрим на какую-то случайно выбранную звезду, то понадобятся сотни тысяч лет, пока еще какой-то умеренно массивный объект (другая звезда, бурый карлик или компактный остаток) пролетит столь близко к лучу зрения, что вызовет заметный эффект.
Какие эффекты могут возникать при таком пролете? Во-первых, это просто смещение видимого положения звезды-источника. Такой случай называют астрометрическим линзированием. Наблюдать эффект очень трудно, так как он мал. Но иногда это удается (если знать, куда смотреть с помощью крупных телескопов), а кроме того, спутник Gaia вскоре должен представить много данных по таким явлениям. Но более известным является так называемое фотометрическое микролинзирование, к которому мы и перейдем.
Гравитационная линза всегда работает таким образом, что усиливает блеск источника. Для этого он должен оказаться на небольшом угловом расстоянии от линзы – внутри так называемого конуса Эйнштейна. Если считать, что источник расположен гораздо дальше линзы, то этот кружок на небе характеризуется угловым радиусом, вычисляемым по очень простой формуле (вот только вывод ее не так уж прост, и здесь мы его приводить не будем):
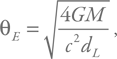
где dL– расстояние от наблюдателя до линзы, а М – ее масса.
Если подставить звездную массу и расстояние порядка нескольких тысяч световых лет, то мы получим угол примерно в несколько сотых угловой секунды. Вероятность того, что одна из звезд попадет в такой кружок, крайне мала, поэтому и надо ждать сотни тысяч лет, пока это произойдет. Но если уж такое случилось, то блеск звезды возрастает в несколько раз, что легко заметить.
С появлением цифровых приемников излучения, чья главная характеристика – число мегапикселей, астрономы научились сразу измерять блеск большого числа звезд. Это дало возможность начать специальные программы наблюдений, охотящихся за случаями микролинзирования. Сейчас счет зарегистрированным событиям идет на многие тысячи.
А что же черные дыры? Насколько часто в роли линзы может выступить такой объект? Чтобы в этом разобраться, нам надо сравнить количество и массы обычных звезд, черных дыр, а также нейтронных звезд и белых карликов.
Начнем с масс. Наблюдения говорят нам, что средняя масса белых карликов составляет примерно 0,6 солнечных, нейтронных звезд – 1,3, а черных дыр – 5–10. Для обычных звезд мы снова воспользуемся начальной функцией масс в виде:

Масса звезд в интервале dM в окрестности какой-то массы M равна просто произведению этой массы на dN. Соответственно, полная масса звезд будет пропорциональна интегралу
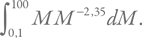
А полное количество звезд, как и выше в приложении 4А, – интегралу
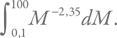
Коэффициент пропорциональности одинаковый. Соответственно, средняя масса звезды, равная отношению массы всех звезд к их количеству, будет отношением этих интегралов. Учитывая, что нижний предел гораздо меньше верхнего, а под интегралом стоят отрицательные степени, по модулю большие единицы, мы получим, что отношение примерно равно 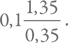 . Это дает 0,38. Обычно используется средняя звездная масса, равная 0,3, поскольку в качестве нижнего предела подставляется неокругленное значение 0,08 солнечных масс.
. Это дает 0,38. Обычно используется средняя звездная масса, равная 0,3, поскольку в качестве нижнего предела подставляется неокругленное значение 0,08 солнечных масс.
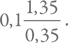 . Это дает 0,38. Обычно используется средняя звездная масса, равная 0,3, поскольку в качестве нижнего предела подставляется неокругленное значение 0,08 солнечных масс.
. Это дает 0,38. Обычно используется средняя звездная масса, равная 0,3, поскольку в качестве нижнего предела подставляется неокругленное значение 0,08 солнечных масс.Итак, звезды в среднем вдвое легче белых карликов, примерно в пять раз – нейтронных звезд и примерно в 20 раз – черных дыр. Это важно, так как для этих объектов будут пропорционально квадратному корню из массы изменяться параметры конусов Эйнштейна.
Теперь оценим относительное количество этих четырех типов объектов. Выше, в приложении 4А, мы уже сравнивали количество черных дыр с количеством звезд. Аналогичным способом, меняя пределы интегралов, можно получить, что нейтронных звезд примерно в 5 раз, а белых карликов раз в 20 больше, чем черных дыр.
Собирая все вместе, получаем, что почти 90 % случаев линзирования должны быть связаны с обычными звездами. Примерно в 10 % случаев линзами могут являться белые карлики, а вот на долю нейтронных звезд и черных дыр вместе приходится около 1–2 % (вклад нейтронных звезд несколько уменьшается из-за их высокой скорости, так как они быстро покидают диск Галактики). Однако, поскольку случаев линзирования известно уже более десяти тысяч, то и 1 % – это хорошо.
В самом деле, на сегодняшний день выявлено более десятка случаев линзирования, где линзой является нейтронная звезда или черная дыра. Здесь первый шаг таков. Данные наблюдений позволяют получить распределения вероятностей для массы линзы и расстояния до нее. Затем мы можем попытаться увидеть объект, выступивший в роли линзы. При типичных массах нейтронных звезд и черных дыр это были бы довольно заметные звезды. Таким образом, если ничего не удается увидеть, то это сильный аргумент в пользу того, что мы имеем дело именно с компактным объектом, а не с обычной звездой.
На втором шаге нам надо попробовать различить нейтронные звезды и черные дыры. И тут подход очень прост. Если масса темной линзы превосходит три солнечных, то объект считают черной дырой. На сегодняшний день выявлено несколько таких кандидатов. Из-за значительной массы черных дыр и их относительно небольшой скорости продолжительность событий линзирования на таких объектах весьма велика – обычно более года! Так что времени для детального построения кривой блеска источника предостаточно. Проблема в том, что мы не можем изучать, не можем (пока?) никаким способом идентифицировать черную дыру по окончании эпизода линзирования. Поэтому часть коллег считают, что все такие кандидаты недостаточно надежны. Тем не менее на сегодня это единственный, хоть как-то работающий способ получать прямую информацию об одиночных черных дырах звездных масс.
4B. Испарение
Одним из самых потрясающих открытий, которые к тому же могут произойти в любой момент (надо только много-много везения), было бы обнаружение испарения черных дыр. Это не только доказало бы существование хокинговского излучения, не только стало бы самым надежным доказательством существования черных дыр, но вдобавок дало бы нам в руки уникальный инструмент по проверке моделей квантовой гравитации.
Как мы увидим в дальнейшем, только очень легкие черные дыры могут дойти до финальных стадий испарения за 13–14 млрд лет – время жизни вселенной. В настоящее время испаряются черные дыры, имевшие вначале массы порядка 1015 г, а черные дыры тяжелее 1026 г (это примерно масса Луны) вообще наращивают массу, а не уменьшают ее. Откуда же берутся такие черные дыры?
Еще в конце 1960-х гг. начали обсуждать возможность рождения черных дыр в молодой вселенной, когда плотность вещества была очень велика (одними из первых такие идеи высказали Яков Зельдович и Игорь Новиков). А начиная с 1970-х гг. благодаря трудам Стивена Хокинга и других ученых эта идея стала весьма популярной гипотезой, в верности которой сейчас мало кто сомневается.
Сама идея крайне проста, и ее можно объяснить «на пальцах». Уже в самые ранние эпохи существования вселенной (первые доли секунды) плотность не распределена равномерно. Из-за флуктуаций (в инфляционной модели за эти вариации плотности ответственны квантовые эффекты) вещество распределено «где-то густо, а где-то пусто». Под действием гравитации области повышенной плотности могут сжиматься, а если масса и размер области соответствуют параметрам черной дыры, то и коллапсировать.
Существенно, однако, что вселенная еще очень молода. Поэтому сигналы (в том числе гравитационное взаимодействие) успели распространиться лишь на небольшое расстояние. Как говорят, «горизонт еще мал», т. е. размеры причинно-связанных областей невелики. Коллапсировать может лишь причинно-связанная область (иначе одна часть «не знает» о гравитационном влиянии другой). Если критическая комбинация массы и радиуса достигается лишь при большем размере, то придется подождать. По мере жизни вселенной размер горизонта растет как произведение времени на скорость света. Но не будем забывать, что и сама вселенная расширяется! Иначе говоря, области повышенной плотности могут растягиваться. И тут уж «кто кого переборет»: или размер горизонта успеет дорасти до нужного масштаба и произойдет коллапс, или флуктуация растянется и формирования черной дыры удастся избежать.
Важно, что коллапсирует область размером порядка текущего горизонта. Соответственно, в разное время формируются черные дыры разной массы: чем позже – тем больше. Процесс идет от самых ранних моментов (когда теоретически в некоторых моделях масса может доходить до планковской – 10–5 г) до примерно одной секунды (тогда могут образовываться дыры с массой около 100 000 масс Солнца). Для массы черной дыры в зависимости от времени формирования существует простая формула, определяемая массой вещества внутри горизонта:

где c – скорость света, G – ньютоновская постоянная, а t – время.
Результат приведен в граммах, и время нормировано на момент формирования тех дыр, чья жизнь сейчас, согласно хокинговской модели, подходит к концу.
В своей знаменитой работе 1975 г. Стивен Хокинг предложил механизм, с помощью которого черная дыра может «испаряться». Детали механизма довольно нетривиальны с бытовой точки зрения, а упрощенные иллюстрации лишь вводят в заблуждение. Но, как бы то ни было, вблизи горизонта (что не означает микроскопических расстояний от него!) за счет квантовых эффектов формируются частицы (и кванты электромагнитного излучения, и частицы, имеющие массу покоя), уносящие энергию дыры, т. е. уменьшающие ее массу. Чем меньше черная дыра, тем активнее она излучает. Для внешнего наблюдателя черная дыра выглядит как источник теплового излучения.
Температура излучения черной дыры определяется следующей формулой:
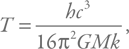
где h – постоянная Планка, а k – постоянная Больцмана.
Видно, что с уменьшением массы температура растет. Давайте попробуем получить эту формулу с точностью до численного коэффициента.
Начнем мы, как ни странно, с принципа неопределенности Гейзенберга и корпускулярно-волнового дуализма. Легенда гласит, что в разговоре с Яковом Борисовичем Зельдовичем Владимир Наумович Грибов высказал следующую мысль. Возникает парадокс, если мы применим принцип Гейзенберга к черным дырам. С одной стороны, мы говорим, что из них ничего не вылетает, а с другой – как же мы локализуем в маленькой черной дыре частицу, длина волны которой превосходит размер черной дыры? Иными словами, в некотором смысле квантовая механика вступает в противоречие с ОТО. Грибов полагал, что «квантовая механика победит».
Предельный масштаб, на котором мы можем локализовать частицу, связан с ее комптоновской длиной волны:
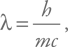
где m – масса частицы.
Что же это за длина волны? Это можно пояснить таким образом (хотя в таком упрощенном комментарии есть элемент передергивания). Каждой длине волны соответствует частота, которую можно рассчитать, используя скорость распространения волны. В данном случае – скорость света: ν = c /λ. С одной стороны, если мы рассматриваем волну, то энергия частицы будет равна E = hν. С другой – энергия частицы при такой предельной локализации будет порядка ее энергии покоя: E = mc2. Таким образом, hν = hc /λ = mc2. А отсюда мы сразу получаем, что
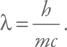
Принцип неопределенности Гейзенберга записывается таким образом:
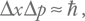
где Δx – неопределенность координаты, а Δp – неопределенность импульса частицы.
В нашем рассуждении существенно, что мы пытаемся локализовать частицу по координате с точностью порядка ее комптоновской длины волны. Это приведет к тому, что неопределенность импульса будет порядка Δp = mc (именно поэтому выше мы могли использовать скорость света при сопоставлении частоты и длины волны). Тогда для Δx получим:
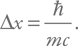
Таким образом, эта величина равна комптоновской длине волны, деленной на 2π. Эту величину называют приведенной комптоновской длиной волны и записывают так: 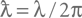 (а величину
(а величину 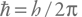 называют приведенной или редуцированной постоянной Планка).
называют приведенной или редуцированной постоянной Планка).
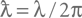 (а величину
(а величину 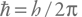 называют приведенной или редуцированной постоянной Планка).
называют приведенной или редуцированной постоянной Планка).Теперь получим оценку температуры черной дыры. С одной стороны, пределом для «вылезания» частицы из дыры будет равенство диаметра черной дыры и приведенной комптоновской длины волны (напомним, что мы всего лишь даем некую иллюстрацию, на самом деле никакие частицы из черной дыры не «вылупляются», они не пересекают горизонт «оттуда сюда», а возникают «с нашей стороны» из-за изменений параметров вакуума, связанных с нестационарностью горизонта). С другой стороны, при излучении у нас есть равенство для тепловой энергии частицы и энергии кванта:

где длина волны – это комптоновская длина.
Приведенную длину мы оценили как удвоенный радиус черной дыры, для которого используем стандартную формулу Шварцшильда:
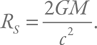
Таким образом получаем:
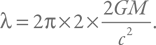
Теперь соберем все вместе и получим выражение для температуры:
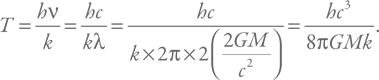
Формула лишь коэффициентом π отличается от точного значения. Разумеется, это совсем не строгий вывод, и, только зная аккуратно полученный правильный результат, можно потирать руки, радуясь тому, что мы таким простым способом получили столь фундаментальную формулу. Тем не менее приятно, что можно построить такую наглядную цепочку рассуждений.
Отметим, что при уже упоминавшейся массе 1026 г температура будет примерно равна современной температуре реликтового излучения, заполняющего всю вселенную (в прошлом температура была выше). Так что, даже если мы сейчас поместим черную дыру в совсем пустую область космоса, она все равно будет расти за счет поглощения фотонов реликта при массе больше 1026 г.
Итак, у нас есть температура, значит, в первом приближении мы можем посчитать светимость. Для теплового излучения сферы радиуса R она рассчитывается по формуле

Напомним, что постоянная Стефана – Больцмана равна:
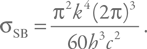
В качестве радиуса излучающей поверхности подставим шварцшильдовский радиус. Затем светимость запишем в таком виде:
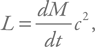
т. е. мощность излучения определяется темпом потери массы. Тогда мы сможем записать:
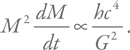
Проведем интегрирование от начальной массы M до нуля (полное испарение) и для времени полного испарения получим:
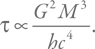
Точная формула выглядит так:
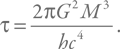
Мы снова с точностью до численных коэффициентов получили верный результат!
Можно получить его и несколько иначе. Пусть энергия уносится квантами электромагнитного излучения (напомним, что на первых этапах испарения, пока температура недостаточно велика, частицы не рождаются – только излучение). Энергия одного кванта равна  Характерное время испускания составляет Δt = λ/ c. Запишем вначале такое выражение (оно соответствует светимости L):
Характерное время испускания составляет Δt = λ/ c. Запишем вначале такое выражение (оно соответствует светимости L):
 Характерное время испускания составляет Δt = λ/ c. Запишем вначале такое выражение (оно соответствует светимости L):
Характерное время испускания составляет Δt = λ/ c. Запишем вначале такое выражение (оно соответствует светимости L):
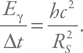
Значит:
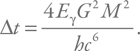
Нам надо оценить время излучения всей массы черной дыры, т. е. время потери энергии E = Mc2. Обозначим это время, как и выше, буквой τ и вместе с Eγ подставим в уравнение E = Mc2. Это можно описать и иначе:
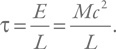
Получим:
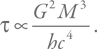
Иначе говоря, снова тот же результат, верный с точностью до небольшого численного коэффициента.
Когда температура черной дыры становится достаточно высокой для того, чтобы рождались не только кванты электромагнитного излучения, но и частицы, коэффициент в формуле немного изменяется. Поэтому для совсем легких черных дыр формула работает лишь примерно: они испаряются несколько быстрее.
Что здесь для нас важно с точки зрения астрофизики? Испаряющиеся черные дыры являются уникальными источниками, проявления которых можно надеяться выявить. Здесь астрономы идут разными путями.
Во-первых, можно искать сами вспышки, связанные с последними моментами жизни черных дыр, причем как в гамма-диапазоне (ведь температура растет с падением массы, и на финальных стадиях испускается много гамма-излучения), так и в других, в первую очередь в радиодиапазоне. К сожалению, ничего пока не обнаружено. Заметим, что на финальных стадиях, несмотря на высокую температуру, светимость объекта невелика (намного меньше солнечной). Действительно, ведь от черной дыры почти ничего не осталось – за последнюю десятую долю секунды испаряются последние тонны вещества (а за последнюю минуту – несколько сотен тонн). Поэтому вспышки в гамма-диапазоне (где их легче искать) доступны с помощью современной аппаратуры лишь с расстояний порядка одного парсека и меньше.
Остроумный подход использовала коллаборация спутника Fermi. Допустим, мы могли пропустить вспышку (или ни один из аппаратов не смотрел в нужную сторону, или вспышка была слаба, или еще что-то помешало, например солнечная активность). Но за годы до момента своего исчезновения достаточно близкая черная дыра является заметным гамма-источником, чьи светимость и спектр меняются по более или менее известному закону. А кроме того, поскольку объект достаточно близкий, можно заметить его смещение на небе. Соответственно, был проведен поиск источников, которые исчезли за несколько лет мониторинга всего неба в гамма-диапазоне обсерваторией «Ферми», и при этом определенным образом эволюционировали их светимости и спектральные параметры, а также изменялись координаты. Опять-таки ничего обнаружить не удалось, но был дан самый жесткий предел на темп испарения черных дыр в наших окрестностях: менее десятка тысяч событий в год в объеме один кубический парсек.
Второй путь связан не с поиском вспышек, а с попытками обнаружить суммарный вклад множества испаряющихся черных дыр. Во-первых, можно искать «лишнее» гамма-излучение. Например, от черных дыр в центральной части нашей Галактики или от соседних галактик. А во-вторых, можно искать частицы, рождающиеся на финальных стадиях испарения, причем не просто частицы, а античастицы.
Чтобы выполнялся закон сохранения электрического заряда, частицы должны рождаться парами: электроны-позитроны, протоны-антипротоны. Электронов и протонов вокруг много – трудно выявить лишние, а вот позитронов и антипротонов – мало. Понятно, что в тарелке супа проще обнаружить лишнюю ложку соли, чем лишнюю ложку воды. Вот и астрофизики ищут избыток античастиц. Пока также ничего не выявлено, однако попытки обнаружить сигнал продолжаются. Например, недавно появились интересные результаты со спутников «Вояджер», вылетевших за пределы гелиосферы. За гелиопаузой проще обнаружить лишние позитроны, так как солнечный ветер и относительно большое магнитное поле во внутренних частях Солнечной системы не мешают их распространению. Увы, снова ничего.
Наконец, черные дыры можно искать способами, описанными нами в приложениях 4А и 4Б: с помощью микролинзирования и поиска аккрецирующих источников. Такие работы были проведены, и тоже с нулевым результатом. Хотя… В 2019 г. появилась работа, в которой представлены шесть ультракоротких событий линзирования по данным проекта OGLE. Не исключено, что это могут быть первичные черные дыры с массами порядка земной. Хотя более вероятно, что это просто блуждающие одинокие планеты.
Подведем итоги. Все основные космологические модели предсказывают, что в первые доли секунды существования вселенной должны были возникать черные дыры. Таких объектов может быть много, и иногда их даже обсуждают как кандидатов для объяснения хотя бы части темного вещества. Тем не менее, несмотря на применение разнообразных методов поиска, пока ничего не обнаружено. Теория не может дать надежного предсказания о количестве таких объектов. Поэтому поиски продолжаются, и в любой момент кому-то может повезти. Как говорил Семен Семенович Горбунков, «будем искать».
Назад: Приложение 3 Аккреция, предельная светимость и массы сверхмассивных черных дыр
Дальше: Приложение 5 Астрофизика нейтронных звезд

