Возьмем предмет, поднимем его над полом и отпустим. Он со стуком упадет. Звук – это продольные волны, распространяющиеся в среде и переносящие энергию. Откуда взялась эта энергия в случае падающего тела? Ответ дается в школьном курсе физики. Там рассказывается, что тело на высоте h имеет так называемую потенциальную энергию E_p = mgh, где m – масса тела, а g – ускорение свободного падения. Ускорение можно рассчитать из закона всемирного тяготения:

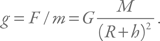
где G – ньютоновская постоянная, M – масса Земли, а R – ее радиус.

В школьных задачах чаще всего можно считать, что высота, с которой падает тело, намного меньше радиуса Земли (R >> h), поэтому g не изменяется.

При падении тело разгоняется, так как на него действует сила в направлении движения. Растет кинетическая энергия, равная:

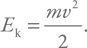
Этот рост происходит за счет уменьшения потенциальной энергии. К моменту удара, как учит нас школьный учебник, вся потенциальная энергия успела перейти в кинетическую. Затем практически мгновенно вся кинетическая энергия перейдет в другие формы, например в тепловую энергию и в энергию звуковой волны. В бытовых ситуациях тепловой эффект мы обычно не замечаем, но вот если на Землю падает крупный метеорит, то нагрев более чем заметен, свидетельством чего являются так называемые тектиты – оплавленные куски стекла, возникающие из-за нагрева пород при ударе.

Школьное описание является несколько упрощенной версией. Нас будет интересовать падение вещества на нейтронные звезды и черные дыры, при этом расстояние, с которого оно прилетает, намного больше размеров компактных объектов. Для такого случая запишем потенциальную энергию более корректно:

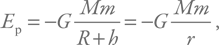
где M – масса массивного тела, а m – масса падающего объекта (в такой постановке M >> m).

Буквой r мы обозначили расстояние, с которого прилетает вещество, отсчитывая его от гравитирующего центра (т. е. от центра массивного тела).

Вы уже обратили внимание, что потенциальная энергия отрицательна. Она отражает, насколько сильна связь между телами, т. е. сколько нужно энергии, чтобы эту связь разорвать. Скажем, если объект покоится на поверхности массивного тела, то, сообщив ему кинетическую энергию, меньшую, чем модуль потенциальной энергии, но бóльшую, чем его половина, мы сможем вывести его на орбиту. А в результате передачи кинетической энергии, большей модуля потенциальной, объект перестанет быть гравитационно связанным с массивным телом, поскольку сумма потенциальной и кинетической энергии станет положительной.

Нас сейчас будет интересовать аккреция вещества, т. е. его падение на гравитирующий центр. Полная энергия для частиц такого вещества будет отрицательной (мы не рассматриваем случай, когда частицы просто «влетают в лоб», т. е. случайно имеют траекторию движения, пересекающуюся с поверхностью тела). При падении потенциальная энергия уменьшается (отрицательная величина растет по модулю). Значит, должны расти другие виды энергии, имеющие положительное значение, и по крайней мере часть этой энергии может быть излучена. Поэтому в астрофизике аккреция нередко приводит к появлению заметных источников излучения.

Возьмем один грамм вещества на большом расстоянии от массивного тела. Пусть вначале скорость вещества пренебрежимо мала, т. е. его полная энергия примерно равна потенциальной (тут мы не учитываем энергию покоя и внутреннюю энергию вещества). Если расстояние достаточно велико (как говорят, «вещество падает из бесконечности»), то энергия равна нулю. При достижении поверхности потенциальная энергия для единичной массы (m = 1) станет равной E_p = –GM / r.

Но полная энергия должна оставаться нулевой, т. е. излучена может быть энергия, равная по модулю E_p (обычно не вся эта энергия излучается, часть перейдет в другие формы). Оценим, насколько эта величина может быть велика.

При падении на Землю (если пренебречь влиянием атмосферы) энергия от падения 1 грамма вещества составит примерно 6 × 10¹¹ эрг (или 60 кДж). Это всего лишь 15 г в тротиловом эквиваленте. Но если мы теперь возьмем массу километрового астероида, то получим около 20 000 Мт ТНТ! Много, но с галактических расстояний такое не разглядеть.

Посмотрим на другие источники. Один грамм, упавший на поверхность массивного белого карлика, даст в миллион раз больше, чем при падении на Землю. Иными словами, примерно 40 граммов дадут одну килотонну, а в случае нейтронной звезды уже один грамм будет давать несколько килотонн! Это примерно 10 % от E = mc². Вспомним, что термоядерные реакции в недрах звезд имеют КПД всего лишь 0,7 % (т. е. при синтезе гелия из водорода выделяется лишь 0,007 от mc²). Стало быть, нет ничего удивительного в том, что аккрецирующие нейтронные звезды наблюдаются как мощные источники.

А что с черными дырами? Они же еще компактнее нейтронных звезд. Да, но зато у них нет поверхности. Поэтому в принципе падающее вещество может унести энергию с собой под горизонт. Значит, надо заставить вещество выделить ее достаточно близко от него. Такая ситуация реализуется при формировании аккреционных дисков вокруг черных дыр. Вещество, обладающее достаточно большим орбитальным моментом, закручивается в диск вокруг тяготеющего центра. Из-за трения вещество в диске нагревается, что и позволяет излучить значительную долю энергии.

Откуда же взять много вещества, чтобы возник мощный источник? Чтобы за счет аккреции на нейтронную звезду обеспечить светимость, равную солнечной, надо примерно раз в минуту сбрасывать на нее комету. Что может быть регулярным источником такой массы? Во-первых, есть межзвездная среда. Плотность ее невелика, но в некоторых случаях ее может быть достаточно, чтобы одиночная аккрецирующая нейтронная звезда стала заметным источником. Пока такие объекты не открыты, но ждать, видимо, остается недолго. Во-вторых, звезды часто рождаются не поодиночке, а парами. Перетекание вещества (или его перенос за счет звездного ветра) со звезды-соседки на компактный объект может привести к появлению источника большой светимости.

Светимость по порядку величины можно посчитать по такой простой формуле:

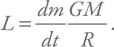
Первый сомножитель dm / dt называют темпом аккреции, он показывает, сколько вещества аккрецирует за единицу времени. Казалось бы, неограниченно наращивая темп аккреции, мы получим сколь угодно большую светимость. Не тут-то было!

Существует предельное значение светимости, которое носит имя Артура Эддингтона, – эддингтоновская светимость. Физика здесь довольно проста: свет оказывает давление. Значит, если поток излучения слишком велик, то он будет попросту «сдувать» лишнее вещество. Установится некоторый баланс между действием гравитации, стремящейся притянуть как можно больше вещества, и излучением, поток которого растет по мере возрастания темпа аккреции. Попробуем получить формулу для эддингтоновской светимости.

Рассмотрим водородную плазму, поскольку типичный – так называемый солнечный – состав вещества звезд соответствует водородно- гелиевой смеси, на 90 % по числу атомов состоящей из самого легкого элемента. У нас есть частицы всего двух сортов: тяжелые протоны и легкие электроны, и их количество равно друг другу, так как вещество должно быть электрически нейтральным. Соответственно, рассмотрим пару электрон-протон.

На частицы действуют две силы: гравитация и давление излучения. Можно считать, что сила тяжести в основном действует на протоны (поскольку они примерно в 2000 раз тяжелее электронов), а давление света – на электроны. И эти силы, приложенные к паре, уравновешивают друг друга.

Рассмотрим вещество у поверхности объекта массой M и радиуса r. С гравитацией все просто:

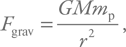
где m_p – масса протона.

Теперь нам надо разобраться с силой, связанной с давлением излучения. Введем величину потока излучения, равную энергии, проходящей через единичную площадь за единицу времени:

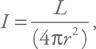
где L – светимость (т. е. мощность источника).

Но нам нужно рассчитать силу, действующую на один электрон. Мы сделаем это так: запишем силу как давление, создаваемое излучением, на площадь.

Поскольку сила действует на электрон, то в качестве площади возьмем так называемое томсоновское сечение, σ_T. По сути, это эффективная площадь электрона при рассеянии на нем электромагнитных волн. Точная формула такова:

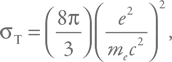
где m_e– масса электрона, а e – его заряд.

Величину e²/m_ec² называют классическим радиусом электрона.

Итак, мы знаем площадь, как теперь оценить давление? Очень просто. Давит излучение. Давление же характеризуется плотностью энергии, т. е. нам надо оценить плотность энергии излучения. Мы знаем поток, или сколько энергии проходит в единицу времени через единичную площадь. Плотность энергии будет равна потоку, деленному на длину, проходимую излучением за единицу времени. Длина равна произведению скорости (в нашем случае это скорость света) на время (т. е. на единицу, так как мы рассматриваем единичный интервал). Для давления получаем: I / c. А для силы:

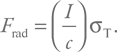
Из равенства F_grav = F_rad получим:

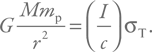
Подставим выражение для I, и тогда:

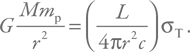
Видим, что равенство не зависит от расстояния. Выражаем светимость (и вводим обозначение L_Edd):

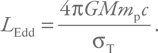
Подставляя характерные значения и константы, получим:

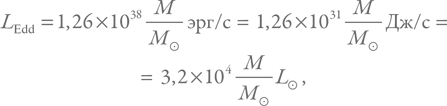
где L_ʘ – солнечная светимость, а M_ʘ – масса Солнца.

Таким образом, для каждой массы центрального объекта (будь то обычная звезда или нейтронная, черная дыра звездной массы или сверхмассивная) есть предельная светимость. Мы рассматривали сферически симметричную геометрию, отклонения от нее могут немного увеличить предельную светимость. Если рассмотреть не чисто водородную плазму, то мы также получим несколько иной результат. Тем не менее предел есть, и он работает.

Наличие предельной светимости позволяет делать оценки массы центральных объектов. Например, если в центре какой-то галактики мы наблюдаем активное ядро, то его светимость позволяет дать нижний предел на массу сверхмассивной черной дыры. И наоборот, знание о диапазоне масс сверхмассивных черных дыр позволяет предсказать диапазон их светимостей. В типичных квазарах массы центральных объектов составляют десятки миллионов солнечных. Значит, светимости квазаров не должны превосходить примерно несколько триллионов светимостей Солнца.

Наконец, ответим еще на один вопрос. В каком диапазоне будет излучать аккрецирующая нейтронная звезда при светимости, близкой к предельной? Это легко оценить. В данном случае можно предположить, что вся поверхность компактного объекта (и/или внутренняя часть аккреционного диска, чья площадь по порядку величины близка к полной площади поверхности нейтронной звезды) нагрета до определенной температуры и излучает так называемое абсолютно черное тело. В таком случае светимость равна:

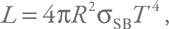
где σ_SB – постоянная Стефана – Больцмана.

Подставив эддингтоновскую светимость и радиус нейтронной звезды 10 км, получим, что температура составляет порядка 20 млн Кельвин. Такая температура соответствует рентгеновскому излучению, поэтому нейтронные звезды в тесных двойных системах с большим темпом аккреции мы наблюдаем именно как рентгеновские источники.