Яркой иллюстрацией того, как с помощью качественных рассуждений можно получать правильные физические формулы, является метод размерностей. Мы рассмотрим здесь два простых примера: параметры в центре Солнца и период пульсаций звезд.

Идея метода крайне проста. Мы хотим получить формулу для расчета какой-то величины A, имеющей определенную размерность. Подумаем, от каких параметров она может зависеть. Пусть это другие величины B, C, D. Обычно зависимости носят степенной характер (т. е. величины входят в конечную формулу в какой-то степени). Возьмем выбранные нами величины, а показатели их степени будут нашими неизвестными: x, y, z. Наше гипотетическое уравнение имеет вид: A = B^xC^yD^z. Теперь существенно, что все это – размерные величины. Размерность обозначают символом величины в квадратных скобках: [A]. Значит, для размерностей должно выполняться то же самое уравнение:

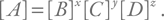
Ведь если слева секунды, то и справа должны получаться секунды, а не сантиметры или граммы. Уравнение для размерностей дает нам систему простых линейных уравнений, решение которой может дать показатели степени x, y, z. Иначе говоря, мы найдем нашу искомую формулу. Конечно, в ней также могут быть безразмерные коэффициенты. С ними разбираться уже сложнее, но иногда и это оказывается возможным. Посмотрим на примеры.

Начнем с оценки давления в центре Солнца (а затем получим температуру, правда, уже не методом размерностей, а используя физику 10-го класса средней школы). Солнце находится в состоянии гидростатического равновесия. Градиент давления (оно растет внутрь) уравновешивает силу тяжести. Значит, давление должно выражаться через параметры, связанные с солнечной гравитацией. Таким образом, в нашу формулу войдет масса Солнца M и гравитационная постоянная G. Сила гравитации зависит от расстояния. Характерный масштаб в задаче – размер Солнца, R. Добавим и его. Тогда для давления получим:

Теперь займемся размерностями. С массой и радиусом все просто: [M] = г, [R] = см. Давление – это в первую очередь плотность энергии, т. е. для него можно записать:

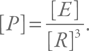
Размерность энергии, выраженную через базовые величины, можно вспомнить благодаря формуле E = mv² / 2: [E] = г см² с^–2. Значит, для давления получим: [P] = г см^–1 с^–2. Остается гравитационная постоянная. Ее размерность, конечно, можно взять из справочника, а можно вспомнить закон всемирного тяготения:

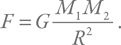
Для размерностей должно выполняться такое же соотношение:

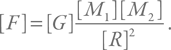
Иначе говоря, [G] = [F][R]² / [M]². Размерность силы (напомним, что сила равна произведению массы на ускорение) равняется г см с^–2. Значит, [G] = г см с^–2 см² г^–2 = г^–1 см³ с^–2. Теперь можно вернуться к нашему уравнению для давления, записав его для размерностей:

Преобразуем правую часть и упорядочим ее, получим:

По отдельности должны выполняться равенства для каждой базовой размерности слева и справа, т. е. имеем систему уравнений: 1 = y – x; –1 = 3x + z; –2 = –2x.

Решая ее, получим: x = 1; y = 2; z = –4.

Иначе говоря, P = GM²R^–4. Это то, что мы и хотели! Формула для расчета давления в недрах Солнца!!! Остается подставить солнечную массу (2·10³³ г) и радиус (696 000 км). Получим, что давление в центре Солнца в 10 млрд раз больше атмосферного давления у поверхности Земли!

Чтобы получить температуру, возьмем формулу для идеального газа из школьного учебника:

где V – объем,  – универсальная газовая постоянная, а  – молярный вес (для простоты можно считать, что Солнце состоит из атомарного водорода). Вместо давления подставим P = GM²R^–4 и преобразуем формулы, выразив температуру:

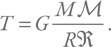
Остается подставить числа. Ответ – температура порядка 20 млн Кельвин. Полученные нами оценки температуры и давления близки к верным значениям.

Аналогично можно получить формулу для периода пульсаций звезды. Правда, здесь ответ будет менее точным из-за наличия безразмерного коэффициента, который нам трудно определить точно таким же методом. Зато зависимость от ключевых величин мы получим правильную.

Снова будем искать формулу для периода в виде G^xM^yR^z. Есть всего лишь один набор показателей степени x, y, z, дающих величину с размерностью времени. Эта комбинация: R^{3 / 2} / (GM)^{1 / 2}. Заметим, что частное от деления массы на куб радиуса имеет размерность плотности. Тогда получим, что период пульсаций звезды (вообще, газового шара), P_puls, пропорционален квадратному корню из произведения гравитационной постоянной на среднюю плотность. А поскольку G – постоянная, то важным фактом является пропорциональность периода пульсаций обратному квадратному корню из плотности:

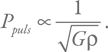
У звезд типа Солнца чем меньше масса, тем выше средняя плотность. Это говорит о том, что с ростом массы растет и период пульсаций. Кроме того, низкая средняя плотность проэволюционировавших и раздувшихся звезд приводит к большим периодам, что и наблюдается. Если у Солнца основной период пульсаций составляет около часа, то у звезд-гигантов он может составлять десятки дней, что неудивительно, ведь их радиусы в сотни раз больше.