Книга: Все формулы мира
Назад: Приложение 4 Одиночные черные дыры
Дальше: Приложение 6 Быстрые радиовсплески
Приложение 5
Астрофизика нейтронных звезд
Нейтронные звезды – одни из самых интересных физических объектов. В результате коллапса ядер массивных звезд формируются тела с массами 1–2 солнечных и радиусами 10–15 км. Столь высокая компактность приводит к ряду экзотических свойств, связанных со сверхвысокой плотностью, сильной гравитацией и мощными магнитными полями. В этом приложении мы обсудим несколько аспектов, связанных с физикой нейтронных звезд, попробовав на уровне простых формул продемонстрировать суть дела, а также сделав ряд количественных оценок.
5А. Магнитные поля нейтронных звезд
Многие особенности нейтронных звезд связаны с тем, что они обладают очень сильными магнитными полями. Если на поверхности Земли поле не превышает 1 Гс, а в лабораторных экспериментах на мгновение удается получить поле в миллион раз больше, то на нейтронных звездах типичными считаются поля в миллион миллионов (1012) Гс! У некоторых магнитаров они еще в тысячу раз выше. Откуда эти поля взялись?
Нейтронные звезды образуются в результате коллапса ядер массивных звезд. Поскольку все звезды имеют магнитное поле, то оно должно достаться в наследство и нейтронной звезде. Более того, в ходе коллапса поле возрастет. Это достаточно легко понять.
Представьте себе звезду, пронизанную линиями магнитного поля. Плотность силовых линий – сколько их проходит через данную площадку – будет определять величину поля. Мысленно выделим ядро и опояшем его по экватору. Начинается коллапс – ядро сжимается. При этом число линий поля внутри кольца, охватывающего экватор, сохраняется (как говорят, «сохраняется магнитный поток»), а площадь поверхности ядра уменьшается, ведь она равна 4πR2, где R – радиус сферы. Значит, будет расти плотность силовых линий, т. е. будет возрастать поле: 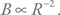 Если до коллапса радиус ядра составлял 10 000 км и в итоге сформировалась нейтронная звезда с радиусом 10 км, то поле возрастет в миллион раз. Поле в ядре незадолго до коллапса может быть заметно выше, чем на поверхности звезды (где поля могут доходить до нескольких тысяч Гаусс), поскольку ядро постепенно поджималось (и уплотнялось) в течение эволюции звезды, так что значения порядка 1 млн Гс не должны быть редкими. В результате после коллапса мы легко получим нейтронную звезду с полем 1012 Гс.
Если до коллапса радиус ядра составлял 10 000 км и в итоге сформировалась нейтронная звезда с радиусом 10 км, то поле возрастет в миллион раз. Поле в ядре незадолго до коллапса может быть заметно выше, чем на поверхности звезды (где поля могут доходить до нескольких тысяч Гаусс), поскольку ядро постепенно поджималось (и уплотнялось) в течение эволюции звезды, так что значения порядка 1 млн Гс не должны быть редкими. В результате после коллапса мы легко получим нейтронную звезду с полем 1012 Гс.
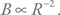 Если до коллапса радиус ядра составлял 10 000 км и в итоге сформировалась нейтронная звезда с радиусом 10 км, то поле возрастет в миллион раз. Поле в ядре незадолго до коллапса может быть заметно выше, чем на поверхности звезды (где поля могут доходить до нескольких тысяч Гаусс), поскольку ядро постепенно поджималось (и уплотнялось) в течение эволюции звезды, так что значения порядка 1 млн Гс не должны быть редкими. В результате после коллапса мы легко получим нейтронную звезду с полем 1012 Гс.
Если до коллапса радиус ядра составлял 10 000 км и в итоге сформировалась нейтронная звезда с радиусом 10 км, то поле возрастет в миллион раз. Поле в ядре незадолго до коллапса может быть заметно выше, чем на поверхности звезды (где поля могут доходить до нескольких тысяч Гаусс), поскольку ядро постепенно поджималось (и уплотнялось) в течение эволюции звезды, так что значения порядка 1 млн Гс не должны быть редкими. В результате после коллапса мы легко получим нейтронную звезду с полем 1012 Гс.Однако, чтобы создать магнитарное поле, которое, напомню, в тысячу раз выше, нужно что-то еще. Скорее всего, на стадии протонейтронной звезды, когда формирующийся компактный объект полностью конвективен (т. е. в нем идут бурные процессы перемешивания вещества), работает так называемый динамо-механизм, усиливающий магнитное поле. Источником энергии для формирующегося гигантского магнитного поля магнитара служит вращение протонейтронной звезды.
Давайте разберемся с энергией вращения и энергией магнитного поля. Представьте себе вращающийся шар. Каждый его маленький кусочек движется по окружности, перпендикулярной оси вращения. Пусть период вращения равен P, а радиус шара – R. Рассмотрим кусочек вещества массой Δm. Он вращается на расстоянии r < R от оси. Его скорость 2πr / P. Значит, он обладает кинетической энергией Δm (2πr / P)2 / 2. Чтобы получить полную энергию, связанную с вращением, нам надо просуммировать энергии всех кусочков вещества. Строго это получается интегрированием по объему шара. Ясно, что полная масса равна M, при этом все кусочки вращаются внутри шара, т. е. их скорости меньше 2πR / P. Значит, полная кинетическая энергия будет меньше, чем 4π2MR2 / 2P2. Насколько меньше, зависит от того, как меняется плотность вещества внутри шара. Для нейтронных звезд она изменяется слабо, поэтому энергия будет ненамного меньше максимальной.
Чтобы упростить запись формул, удобно ввести две величины: угловую частоту вращения и момент инерции. Угловая частота – это просто 2π / P. Обозначим ее буквой ω. Момент инерции (его обозначим буквой I) показывает, насколько инертно тело в смысле вращения, т. е. насколько трудно его раскрутить, а потом – затормозить (смысл примерно как у массы, характеризующей инертность в смысле поступательного движения). Момент инерции шара пропорционален произведению массы на квадрат радиуса (дополнительный безразмерный множитель зависит от распределения вещества в шаре). Энергия вращения запишется теперь в простом виде, напоминающем формулу для кинетической энергии: E = Iω2 / 2. В случае нейтронной звезды I ≈ MR2 что составляет примерно 1045 г·см2. Период вращения может составлять 0,001 секунды. Таким образом, получаем, что энергия вращения нейтронной звезды может достигать колоссальной величины >1052 эрг. Насколько это много? Это больше, чем Солнце излучает за всю свою жизнь! Так что, даже если малую часть этой энергии конвертировать в энергию магнитного поля, можно получить очень большую величину.
Как посчитать энергию магнитного поля? Не будем начинать с самых основ, а сразу скажем, что плотность магнитной энергии (т. е. магнитное давление) вычисляется по формуле: B2/8π. Значит, чтобы узнать примерную магнитную энергию, содержащуюся в нейтронной звезде, надо эту величину умножить на объем звезды (для простоты предполагаем, что поле заполняет весь компактный объект). Если поле на поверхности равно 1012 Гс, то полная энергия будет равна 2·1041 эрг. Совсем немного. Но если поле магнитарное, то энергия возрастает до 1047 эрг, столько Солнце излучает за 1 млн лет. Однако видно, что энергия вращения может быть больше, так что ее хватит для усиления поля.
С чем еще можно сравнить энергию магнитного поля? Например, с потенциальной (гравитационной) энергией нейтронной звезды. Она вычисляется как GM2/R. В типичном случае это составит 4·1053 эрг. Эта величина позволяет понять, каким может быть предельное магнитное поле. Из
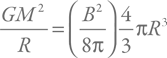
получим, что поле никак не может быть больше 1018 Гс, иначе звезду «разорвет».
У нас нет примеров нейтронных звезд со столь сильными полями; скорее всего, в природе они не встречаются. Но уже типичные магнитарные поля могут искажать сферическую форму нейтронной звезды, ведь магнитное поле распределено в ней неравномерно. Нейтронные звезды могут быть немного вытянутыми вдоль магнитной оси, а могут быть сплюснутыми, что должно сказываться на том, как компактный объект вращается, поэтому есть надежда увидеть это в данных наблюдений. Кроме того, вращение такого несимметричного объекта (если магнитная ось не совпадает с осью вращения) должно приводить к испусканию гравитационных волн. Не исключено, что детекторы следующего поколения (например, так называемый Телескоп Эйнштейна) смогут зарегистрировать такие сигналы.
Итак, энергии вращения много. Часть можно успеть превратить в энергию магнитного поля, пока компактный объект молод и быстро вращается. А что дальше? Дальше магнитное поле может способствовать постепенному превращению энергии вращения в энергию излучения и улетающих с околосветовыми скоростями частиц. Так работают радиопульсары.
Типичный компактный объект этого типа рождается с вращательной энергией около 1051 эрг и магнитным полем 1012–1013 Гс. Если энергию вращения расходовать медленно, то ее хватит очень надолго. Но пульсары так не умеют. Чем быстрее они вращаются, тем быстрее тормозятся. А значит, тем больше излучают. Светимости молодых пульсаров могут легко превосходить миллион светимостей Солнца. Часть этой энергии уносится электромагнитными волнами, поэтому мы видим такие объекты как яркие источники во всех диапазонах спектра – от радио- до гамма-. Однако, как мы упоминали, основная доля уносится быстро двигающимися (релятивистскими) заряженными частицами. Благодаря этому релятивистскому ветру вокруг многих молодых пульсаров мы видим красивые туманности – плерионы. Самым известным примером здесь является Крабовидная туманность. Если в ней «выключить» радиопульсар, то прекратится «накачка» энергии, и туманность постепенно погаснет.
В деталях механизм излучения пульсаров известен плохо, но его можно наглядно проиллюстрировать и даже получить качественно верное выражение для светимости, пользуясь очень простыми соображениями.
Мы уже рассматривали вращающийся шар и помним, что каждая частица шара вращается со скоростью, равной ωr, где r – расстояние от оси вращения. Иначе говоря, чем дальше частица, тем быстрее она вращается. Теперь представьте, что из шара торчат линии магнитного поля. Они жестко связаны с внешними слоями нейтронной звезды, так что вращаются с той же самой частотой (т. е. с тем же периодом). Теперь, как бусинку на проволоку, мы помещаем на линию магнитного поля частицу. Ее скорость вращения также равна ωr. Но мы уже рассматриваем вращение вне нейтронной звезды, а потому с ростом расстояния можем добраться до скорости света!
Ни частица, ни магнитная линия не могут вращаться со скоростью, превышающей световую. Значит, есть критическое расстояние, на котором замкнутая магнитосфера, заполненная заряженными частицами, перестает существовать. Поверхность, отстоящую от оси вращения на Rl = c / ω, называют световым цилиндром. Вне светового цилиндра будут присутствовать только электромагнитные волны и релятивистские частицы, улетающие от нейтронной звезды. Они-то и уносят энергию вращения, т. е. тормозят пульсар. Теперь, качественно представив себе физическую картину, мы готовы получить формулу для светимости пульсара.
Светимость – это количество энергии, испускаемое в единицу времени. Энергия у нас запасается в магнитосфере внутри светового цилиндра, а характерное время испускания – период вращения (напомним, что P = 2π / ω). Сколько же у нас есть энергии? Снова воспользуемся произведением плотности энергии магнитного поля B2 / 8π на объем, но теперь возьмем объем магнитосферы, а величину поля – на световом цилиндре (нас интересуют самые внешние области с большим объемом, которые могут участвовать в процессе излучения). С расстоянием поле спадает как куб радиуса. Пусть поле на поверхности нейтронной звезды с радиусом R0 равно B0. Тогда для энергии получим:
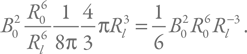
Подставив выражение для радиуса светового цилиндра Rl = c / ω, получим энергию (пренебрегая численными множителями):
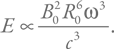
Теперь, чтобы получить светимость, остается разделить это на характерный период. Получим:
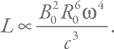
Таким образом, светимость больше для нейтронных звезд с более сильным полем, но, самое главное, она очень быстро спадает с ростом периода: пульсар с периодом 1 с излучает в 10 000 раз меньше, чем при периоде 0,1 с.
Мы уже выписывали уравнение для энергии вращения: Iω2 / 2. Возьмем производную по времени от этой величины. Момент инерции не меняется со временем, поэтому для темпа потерь энергии вращения получим выражение 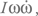 где точка сверху обозначает производную по времени
где точка сверху обозначает производную по времени  Приравняв эту величину к светимости (добавим в формулу для светимости безразмерный коэффициент k, чтобы учесть отброшенные безразмерные множители), получим:
Приравняв эту величину к светимости (добавим в формулу для светимости безразмерный коэффициент k, чтобы учесть отброшенные безразмерные множители), получим:
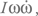 где точка сверху обозначает производную по времени
где точка сверху обозначает производную по времени  Приравняв эту величину к светимости (добавим в формулу для светимости безразмерный коэффициент k, чтобы учесть отброшенные безразмерные множители), получим:
Приравняв эту величину к светимости (добавим в формулу для светимости безразмерный коэффициент k, чтобы учесть отброшенные безразмерные множители), получим:
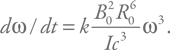
Можно теперь заменить угловую частоту на период и проинтегрировать. Получим, что период нейтронной звезды на стадии радиопульсара возрастает как квадратный корень из времени. Иными словами, если молодая нейтронная звезда возрастом 100 лет имеет период 0,1 с, то к миллиону лет этот период возрастет до 10 с. Это примерно отражает поведение типичного радиопульсара.
Разобравшись с выделением энергии вращения и некоторыми ее свойствами, перейдем к выделению энергии магнитного поля. Да-да, это возможно, ведь поле порождается электрическими токами. А энергию токов мы используем постоянно.
У нейтронной звезды нет батареек, и она не подключена к розетке, поэтому текущие в ней токи со временем затухают, а из-за этого уменьшается магнитное поле. Затухание тока связано с электрическим сопротивлением. Легко сообразить, что сильные токи будут затухать сильнее, а это означает, что сильные поля быстрее уменьшаются. Немного упростив ситуацию, мы можем представить это в виде такой несложной формулы:
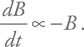
Она показывает, что темп изменения поля (он стоит слева) прямо пропорционален величине поля (она стоит справа), а знак минус указывает на то, что поле со временем становится меньше. Решая это уравнение, мы получим, что поле уменьшается экспоненциально с некоторым характерным временем τ (это время зависит от коэффициентов в уравнении, которые мы обсуждать не будем): 

Энергия тока в таком случае выделяется постепенно, переходя в тепло. Мы с этим постоянно сталкиваемся в быту (пока я пишу эти слова, вскипел чайник, а руками я чувствую, как нагрелся мой ноутбук, – все из-за электрических токов и сопротивления!). Но можно выделять энергию токов быстро – в результате короткого замыкания.
Не пытайтесь проверить, но короткое замыкание – очень эффективный способ быстрого выделения большой энергии. Пожалуй, только так в домашних условиях можно легко оплавить не слишком легкоплавкий металл. Именно с помощью природного электрического пробоя в фильме «Назад в будущее» смогли решить проблему, возникшую из-за поломки ядерного реактора. Если устроить короткое замыкание в коре нейтронной звезды, то можно выделить заметную долю от полной энергии магнитного поля в компактном объекте. Так работают магнитары.
Во время самой мощной из известных магнитарных вспышек пиковая светимость составила примерно 1047 эрг/с. Это более чем 10 000 000 000 000 светимостей Солнца. Намного больше светимости целой галактики! А источником был всего лишь 10-километровый шарик.
Даже если энерговыделение не связано с вращением или диссипацией энергии токов, магнитное поле все равно может оказаться «при деле». Так происходит в аккрецирующих нейтронных звездах.
5Б. Аккрецирующие объекты
В приложениях 3 и 4 мы уже обсудили некоторые особенности процесса аккреции и смогли оценить его высокую эффективность, если вещество падает на массивные компактные объекты. В случае аккреции на поверхность нейтронной звезды каждый грамм вещества выделяет огромную энергию, которую можно оценить как GM / R0, где R0– радиус нейтронной звезды, а M – ее масса. Подставим типичные для этих компактных объектов параметры и получим 1020 эрг на 1 грамм. Это примерно 10 % от mc2! В десять с лишним раз больше, чем у термоядерных реакций в недрах Солнца. Неудивительно, что аккрецирующие нейтронные звезды являются мощными источниками. Теперь посмотрим, какие особенности есть при аккреции на нейтронные звезды, обладающие магнитным полем.
Действие поля возникает из-за того, что падающее вещество является плазмой (преимущественно водородно-гелиевой). Заряженные частицы не могут падать, пересекая линии поля. Поэтому если не возникает неустойчивостей (и если мы пренебрегаем диффузией), то плазма движется только вдоль силовых линий – к магнитным полюсам. Плазма взаимодействует с магнитосферой, а она, в свою очередь, жестко связана с поверхностью нейтронной звезды. В результате компактный объект и вещество могут обмениваться энергией и моментом импульса. Последнее приводит к тому, что вращение нейтронной звезды может замедляться или ускоряться. Однако до стадии аккреции ей еще надо дожить.
Обычно первую часть своей жизни нейтронная звезда проводит как радиопульсар (или на очень похожей стадии, когда доминирует испускание релятивистского ветра частиц, покидающих область светового цилиндра). Но, как мы помним, период вращения пульсара растет, соответственно, уменьшается частота, а ведь светимость пропорциональна последней в четвертой степени! Кроме того, может уменьшаться магнитное поле, при этом светимость пропорциональна ее квадрату. Значит, уменьшается давление, которое ветер частиц и излучение оказывают на окружающую среду.
А среда всегда есть, и это вещество стремится попасть на нейтронную звезду. На каком-то расстоянии давление внешней среды уравновешивается давлением ветра и излучения. Пока это расстояние превосходит размеры светового цилиндра, нейтронная звезда продолжает оставаться эффективным источником частиц. Но вот когда вещество начинает проникать под световой цилиндр, ситуация меняется. Нейтронная звезда переходит на новую эволюционную стадию.
Как правило (если только компактный объект не обладает большой скоростью, превосходящей примерно 400 км / c, относительно межзвездной среды), когда вещество оказалось под световым цилиндром, оно уже гравитационно захвачено нейтронной звездой. Гравитация стремится притянуть вещество к ее поверхности, но на пути встает магнитное поле, ведь вещество является ионизованным (хотя бы частично) газом. Мы уже знаем, что давление магнитного поля пропорционально квадрату величины поля. А поле растет как третья степень расстояния при приближении к компактному объекту. Стало быть, давление увеличивается как шестая степень удаления от поверхности! Очень быстро!
В падающем веществе плотность энергии (т. е. давление) определяется гравитацией. Мы можем оценить давление как ρv2 / 2. Здесь ρ – плотность вещества, а v – его скорость. Скорость есть просто скорость свободного падения:
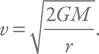
Теперь рассчитаем плотность. Вещество втекает с радиуса гравитационного захвата, о котором мы говорили в приложении 4, с темпом 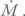 Напомню, что эта величина имеет размерность [г / с]. Поскольку мы рассматриваем сферически симметричную ситуацию, то за единицу времени эти граммы распределяются по объему 4πr2v. Здесь 4πr2 – это площадь сферы, а v – скорость, т. е. расстояние, проходимое веществом за единицу времени. Значит, плотность будет равна:
Напомню, что эта величина имеет размерность [г / с]. Поскольку мы рассматриваем сферически симметричную ситуацию, то за единицу времени эти граммы распределяются по объему 4πr2v. Здесь 4πr2 – это площадь сферы, а v – скорость, т. е. расстояние, проходимое веществом за единицу времени. Значит, плотность будет равна:
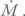 Напомню, что эта величина имеет размерность [г / с]. Поскольку мы рассматриваем сферически симметричную ситуацию, то за единицу времени эти граммы распределяются по объему 4πr2v. Здесь 4πr2 – это площадь сферы, а v – скорость, т. е. расстояние, проходимое веществом за единицу времени. Значит, плотность будет равна:
Напомню, что эта величина имеет размерность [г / с]. Поскольку мы рассматриваем сферически симметричную ситуацию, то за единицу времени эти граммы распределяются по объему 4πr2v. Здесь 4πr2 – это площадь сферы, а v – скорость, т. е. расстояние, проходимое веществом за единицу времени. Значит, плотность будет равна:
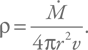
Собираем теперь все вместе, чтобы получить выражение для давления в падающем веществе:
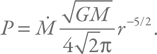
Таким образом, давление повышается при приближении к звезде, но довольно медленно. Значит, более быстрый рост давления магнитного поля приведет к остановке вещества. Это произойдет на расстоянии, которое мы будем называть радиусом магнитосферы, или альвеновским радиусом, названном в честь шведского физика Ханнеса Альвена (Hannes Alfven).
Чтобы определить этот радиус, надо просто приравнять давление падающего вещества к магнитному давлению:
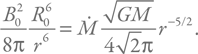
Выразим отсюда радиус, обозначив его RA:
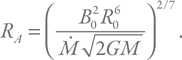
Теперь мы знаем, где магнитное поле останавливает падающее вещество. Если поле слишком слабое или темп аккреции слишком большой, альвеновский радиус может оказаться меньше радиуса нейтронной звезды. Значит, в такой ситуации влиянием поля можно пренебречь. В других случаях его необходимо учитывать.
Мы помним, что вещество представляет собой плазму, а потому не может двигаться поперек силовых линий. Стало быть, плазма будет течь к магнитным полюсам (ситуация похожа на ту, которая приводит к полярным сияниям на Земле). Именно там выделится кинетическая энергия падающего вещества. Из-за этого магнитные полярные шапки на поверхности нейтронной звезды будут горячее остальной поверхности, т. е. будут сильнее излучать. Поскольку компактный объект вращается, то его блеск будет периодически меняться, и возникнет рентгеновский пульсар. Однако не может ли что-то еще предотвратить падение вещества на поверхность?
Падающее вещество сильно взаимодействует с магнитосферой, а она быстро вращается, так как жестко связана с нейтронной звездой. На расстоянии r скорость вращения будет составлять ωr. На каком-то расстоянии эта скорость сравняется со скоростью кругового вращения вещества под действием гравитационного поля. Если радиус магнитосферы больше этого критического расстояния (которое мы назовем радиусом коротации), то вещество будет остановлено: центробежная сила не позволит аккрецирующей плазме достигнуть поверхности. Из-за возникновения центробежного барьера вещество будет отбрасываться быстро вращающимся магнитным полем. Такую стадию назвали пропеллером. А для радиуса коротации мы можем записать простую формулу. Из  получим:
получим:
 получим:
получим:
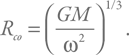
При периоде вращения 10 с радиус коротации равен примерно 10 000 км. Это больше, чем альвеновский радиус нейтронной звезды с магнитным полем 1013 Гс на поверхности и темпом аккреции 1017 г / с (10 % от предельного). Иначе говоря, такая звезда не начнет аккрецировать.
Видно, что радиус коротации уменьшается с ростом частоты (т. е. с уменьшением периода вращения). Значит, быстровращающаяся нейтронная звезда начнет аккрецировать вещество, только если у нее слабое магнитное поле или же очень велик поток вещества (и то и другое приводит к уменьшению альвеновского радиуса). Значит, компактному объекту надо замедлить свое вращение, чтобы аккреция началась. К счастью для наблюдателей, это происходит довольно быстро, так как на стадии пропеллера интенсивное взаимодействие магнитного поля с окружающим веществом приводит к быстрому торможению вращения нейтронной звезды.
В Галактике и ее спутниках – Магеллановых Облаках – известны сотни двойных систем с аккрецирующими нейтронными звездами. Многие из них являются рентгеновскими пульсарами. Предоставляем читателю самостоятельно оценить их типичные периоды вращения из равенства радиуса коротации и альвеновского радиуса при стандартном магнитном поле 1012–1013 Гс и типичном темпе аккреции, соответствующем светимости около 10 % от эддингтоновской.
5В. Атмосферы нейтронных звезд
Как и многие другие тела, нейтронные звезды имеют атмосферу. И как всё у нейтронных звезд, атмосфера у них необычная. Из-за мощной гравитации на поверхности атмосфера оказывается очень тонкой. Мы сможем получить формулу для определения ее толщины, применять которую, кстати, можно не только к нейтронным звездам.
Представьте себе любую атмосферу, например земную. Газ не улетучивается в космос, потому что его удерживает земная гравитация. Но при этом газ и не выпадает на поверхность. Это происходит из-за того, что атмосфера нагрета. Равновесие обеспечивается балансом между силой гравитации и тем, что в нижних слоях атмосферы давление выше. Попробуем разобраться в этом на уровне формул, которые позволят нам сделать и количественные оценки.
Рассмотрим тонкий прямоугольный объем в атмосфере (хотя в целом атмосфера – это сферический слой, но если размер тела намного больше толщины атмосферы, то можно рассмотреть плоский случай). Он имеет массу M и объем V, равный произведению его площади S на толщину нашего тонкого слоя внутри атмосферы dh. Масса складывается из суммы масс отдельных частиц. Будем рассматривать атмосферу, преимущественно состоящую из атомов или молекул одного сорта. Массу одной частицы обозначим m, а их концентрацию (количество в единице объема) n. Тогда:
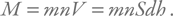
На этот слой действуют три силы: сила давления сверху, сила давления снизу и гравитация. Силу гравитации легко записать: это произведение массы слоя на ускорение свободного падения g. Сила давления – это произведение давления на площадь. Снизу давит сильнее, и если давление снизу мы обозначим P, то сверху оно меньше на небольшую величину dP.
Наш слой находится в равновесии, т. е. силы уравновешивают друг друга:
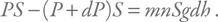
Это уравнение легко упростить, и мы получим – dP = mngdh. dP – отрицательная величина (давление падает с высотой).
Из школьной физики мы помним, что давление в идеальном газе – это плотность энергии движения составляющих его частиц. Каждая частица имеет энергию kT, где T – температура, а k – постоянная Больцмана. Значит, давление равно P = nkT. Можно считать, что в тонком слое температура меняется слабо, а изменение давления связано в первую очередь с уменьшением концентрации частиц при подъеме вверх (атмосфера становится разреженнее). Тогда dP = kTdn, где dn (тоже отрицательная величина) показывает, насколько концентрация частиц внизу слоя больше, чем вверху. Подставим это в нашу формулу и получим:

Теперь перепишем это и получим простое дифференциальное уравнение:
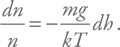
Мы уже сталкивались с похожим уравнением выше, а потому помним, что после интегрирования получим экспоненциальное решение:

где n0 – концентрация частиц на нулевой высоте, а h0=kT / (mg). Последняя величина как раз задает характерную толщину атмосферы: при подъеме на такую высоту концентрация частиц падает в e раз.
Теперь мы можем подставить значения концентрации частиц, температуры и ускорения свободного падения, характеризующие конкретную атмосферу, и получим ее характерную толщину.
В случае Земли температура равна примерно 300К, ускорение свободного падения – 10 м/с2 (что в системе СГС дает нам 1000 см/с2), а масса одной частицы примерно равняется 30 · 10–24 г. Постоянная Больцмана равна 1,38 · 10–16 эрг/К. В итоге получим, что характерная толщина земной атмосферы составляет около 1 млн см, т. е. 10 км.
А что у нейтронных звезд? Если мы говорим о достаточно молодых объектах с возрастами от нескольких сотен до сотен тысяч лет (именно такие компактные объекты удается наблюдать по тепловому излучению их поверхности), то температура составляет примерно 1 млн Кельвин. Типичный состав такой атмосферы – водород (если на нейтронную звезду натекло немного вещества) или железо. Соответственно, массы частиц или около 10–24 г, или 56 · 10–24 г. Ускорение свободного падения гигантское, его можно посчитать как GM / R2, где M – масса, а R – радиус компактного объекта. Получим огромную величину 1014 см/с2, т. е. толщина атмосферы от 1 мм (в случае железа) до 1 см (если основной газ – водород).
Удивительно, но даже такой тонкий слой вещества может сильно влиять на исходящее от поверхности излучение. Без влияния атмосферы мы видели бы от одиночных молодых нейтронных звезд практически идеальный тепловой спектр, а наблюдения показывают, что это не так. Из-за поглощения в толстой (несколько сантиметров!) водородной атмосфере фотоны низкой энергии выходят беспрепятственно лишь из ее внешних слоев, где температура немного ниже. Наоборот, высокоэнергичные кванты рентгеновского излучения (а при 1 млн Кельвин поверхность испускает именно рентген) меньше поглощаются, поэтому достигают наших детекторов из более глубоких слоев. В результате регистрируемый спектр начинает отличаться от чернотельного.
В некоторых случаях природа подкидывает нам интересные загадки: спектр нейтронной звезды может плохо описываться водородным или железным составом. Тогда приходится подбирать нужные ингредиенты. Это не просто подгонка параметров. Дело в том, что после коллапса ядра и взрыва сверхновой часть выброшенного вещества иногда выпадает обратно на компактный объект, поэтому в атмосфере может появиться практически все – от водорода до железа. Что и в каком количестве окажется на поверхности, зависит от параметров взрыва. Таким образом, анализ состава атмосфер молодых нейтронных звезд помогает изучать, как происходят вспышки сверхновых.

