11. Меняя правила. Николай Иванович Лобачевский

На протяжении двух с лишним тысяч лет «Начала» Евклида считались совершенным образцом логически выстроенного научного трактата. Начав с нескольких простых допущений, каждое из которых было сформулировано явно, Евклид постепенно, шаг за шагом, выстроил всю сложную конструкцию геометрии. Он начал с геометрии плоскости, а затем перешел к трехмерной геометрии. Логика Евклида была настолько убедительной, что его геометрия рассматривалась не просто как удобное идеализированное математическое представление видимой структуры физического пространства, но как реальное его описание. За исключением сферической геометрии – геометрии сферической поверхности, которая широко используется в навигации как хорошая аппроксимация формы Земли, – среди математиков и других ученых царило мнение о том, что Евклидова геометрия – единственная возможная геометрия и потому именно она определяет структуру физического пространства. Сферическая геометрия – это не другой тип геометрии; это та же самая геометрия, ограниченная пределами сферы, погруженной в Евклидово пространство. Точно так же, как плоская геометрия – это геометрия плоскости в Евклидовом пространстве.

Вся геометрия Евклидова, другой не бывает.

Одним из первых заподозрил, что это чепуха, именно Гаусс, но он, как обычно, не спешил публиковать результаты, считая, что такая публикация разворошит муравейник. Наиболее вероятной реакцией на подобное заявление стали бы непонимающие взгляды и обвинения – и хорошо если в невежестве, а не в безумии. И вообще, осмотрительный первопроходец выбирает те районы джунглей, где никто не будет выкрикивать ему вслед оскорбления с верхушек деревьев.

Николай Иванович Лобачевский оказался более храбрым – а может быть, более безрассудным или более наивным, – чем Гаусс. Вероятно, и то, и другое, и третье. Разработав геометрию, альтернативную Евклидовой, столь же логичную, как и ее знаменитая предшественница, со своей замечательной внутренней красотой, он понял ее значимость и изложил свои мысли в книге «Геометрия», работа над которой была завершена в 1823 г. В 1826 г. он обратился в физико-математическое отделение Казанского университета с просьбой разрешить ему прочитать лекцию по этой теме, и в конечном итоге статья увидела свет в малоизвестном журнале «Казанский вестник». Он также представил статью в престижную Санкт-Петербургскую академию наук, но Михаил Остроградский, специалист по прикладной математике, отверг ее. В 1855 г. Лобачевский, ослепший к тому времени, продиктовал новый текст по неевклидовой геометрии, озаглавленный «Пангеометрия». Сама же «Геометрия» в первоначальном виде была издана в 1909 г., через много лет после смерти ученого.

Замечательные открытия Лобачевского, наряду с открытиями еще более несправедливо отвергнутого математика Яноша Бойяи, сегодня признаны началом гигантской революции в представлениях человечества о геометрии и природе физического пространства. Но такова вечная судьба первопроходцев – не встречать понимания и подвергаться гонениям. Идеи, которые должны были бы, в принципе, привлекать всеобщее внимание своей оригинальностью, обычно сразу же объявляют чепухой, а их создатели нигде не встречают понимания. У них гораздо больше шансов встретить враждебность – вспомните хотя бы теорию эволюции и изменения климата. Мне иногда кажется, что род человеческий недостоин своих великих мыслителей. Когда они пытаются показать нам звезды, предрассудки и недостаток воображения тянут нас всех назад, в грязь.

В данном случае человечество было едино в своем убеждении: геометрия должна быть Евклидовой. Философы, такие как Иммануил Кант, добирались до невероятных глубин интеллекта, чтобы объяснить, почему это неизбежно. Это убеждение было основано на давней традиции, подкрепленной трудами многих поколений школьников, принужденных осваивать мудреные аргументы Евклида; эти уроки всегда служили своеобразной проверкой памяти. Люди по природе своей склонны ценить знания, которые достаются большим трудом: если геометрия Евклида не есть геометрия реального пространства, то все эти усилия, получается, были потрачены напрасно. Другой причиной была соблазнительная мысль, которую с тех пор окрестили «аргументом к невероятности». Ну конечно, единственно возможная геометрия – Евклидова. Какая же еще?

На риторические вопросы иногда даются риторические ответы, и этот конкретный вопрос, воспринятый всерьез, завел математиков в глухие интеллектуальные дебри. Первоначальной мотивацией служила одна из особенностей трактата «Начала» Евклида, в котором обнаружился недочет. Не ошибка, а всего лишь нечто, казавшееся недостаточно элегантным и в каком-то смысле лишним. Евклид организовал свое изложение геометрии последовательно, в логическом порядке, а начал с простых допущений, которые были сформулированы явно и не доказывались. Все остальное затем выводилось логически из этих допущений, шаг за шагом. По большей части допущения эти были просты и разумны: «все прямые углы равны между собой», к примеру. Но одно из них было настолько сложным, что выделялось в общем ряду, как белая ворона в стае.

Это утверждение известно как аксиома (или постулат) о параллельных, потому что на самом деле речь здесь идет о параллельных прямых. Если две прямые линии параллельны, они никогда не пересекаются. В данном случае аксиома о параллельных гласит, что сумма внутренних углов в этом случае должна быть равна в точности удвоенному прямому углу – 180°. И наоборот, углы будут именно такими, если прямые параллельны.

Понятие о параллельных прямых фундаментально и очевидно: достаточно взглянуть на линованную бумагу. Представляется самоочевидным, что такие прямые существуют и они, разумеется, никогда не встретятся, потому что расстояние между ними всюду одинаково и, соответственно, не может стать нулевым. Евклид наверняка создал проблему на пустом месте, ведь все так очевидно! Возникло общее ощущение, что должна существовать возможность доказать аксиому о параллельных, используя остальные Евклидовы допущения. Мало того, некоторые (таких людей было несколько) были убеждены, что сделали это, но ни одно из подобных доказательств не выдержало проверки: независимые математики всегда обнаруживали в них ошибку или незамеченное спорное допущение.

Одну из первых попыток разрешить этот вопрос предпринял в XI в. Омар Хайям. Я упоминал его работу, связанную с кубическими уравнениями, но это был ни в коем случае не единственный его взнос в математическую копилку. Его «Комментарии к трудностям во введениях книги Евклида» построены на более ранней попытке Хасана ибн аль-Хайсама (в латинизированном варианте Альхазен) доказать аксиому о параллельных. Хайям логически отверг доказательство Ибн аль-Хайсама, как и другие «доказательства», и заменил их рассуждениями, в которых свел аксиому о параллельных к более интуитивно понятному утверждению.

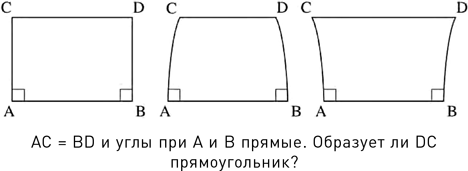
Один из ключевых чертежей Хайяма точно отражает суть проблемы. Его можно рассматривать как попытку построения прямоугольника – совершенно честную, можно сказать, попытку. Проводим прямую линию и строим под прямым углом к ней два отрезка прямых равной длины. Наконец, соединяем вторые концы этих отрезков, чтобы получить четвертую сторону прямоугольника. Готово!

Или нет? Откуда мы можем знать, что получившаяся в результате фигура – прямоугольник? В прямоугольнике все углы прямые, а противоположные стороны равны. На рисунке Хайяма мы видим, что два угла заведомо прямые и одна пара сторон одинакова. А что с остальными?

Да, согласен, все выглядит так, будто мы нарисовали прямоугольник, но это потому, что мы невольно пользуемся геометрией Евклида как мысленным ориентиром. И действительно, в Евклидовой геометрии мы можем доказать, что CD = AB и углы C и D тоже прямые. Однако этот вывод требует применения… той самой аксиомы о параллельных. Это едва ли можно считать удивительным, поскольку мы ожидаем, что CD будет параллельно AB. Если вы хотите доказать аксиому о параллельных на основании прочих аксиом Евклида, вам придется доказать, что Хайям нарисовал прямоугольник, не прибегая к аксиоме о параллельных. Более того, как понял Хайям, если вам удастся это доказать, дело будет сделано. Сама аксиома о параллельных напрямую из этого следует. Пытаясь избежать ловушки, связанной с попыткой доказать аксиому о параллельных, Хайям заменил ее на более простое предположение: «Две сходящиеся прямые пересекаются; невозможно, чтобы две сходящиеся прямые расходились в том же направлении, в каком они сходятся». И он вполне отчетливо понимал, что это действительно допущение.

Джованни Саккери развил чертежи Хайяма – а может быть, пришел к тем же результатам независимо, – но сделал при этом шаг назад, попытавшись с их помощью доказать аксиому о параллельных. Его «Евклид, очищенный от всех пятен» вышел в 1733 г. Он разбил свое доказательство на три возможных варианта, в зависимости от того, является ли угол C на рисунке прямым, острым (то есть меньшим, чем прямой) или тупым (большим, чем прямой). Саккери доказал, что, каким бы ни был тип угла C на одном таком чертеже, ровно таким же он будет и на любом другом чертеже подобного рода. Углы, о которых идет речь, все будут либо прямыми, либо острыми, либо тупыми. Таким образом, существует всего три общих случая, а не три случая для каждого прямоугольника в отдельности. Это большой шаг вперед.

Стратегия доказательства Саккери состояла в том, чтобы рассмотреть альтернативные варианты острых и тупых углов с целью отвергнуть их, распознав какое-либо противоречие. Сначала он предложил считать угол тупым. Это привело к результатам, которые он счел несовместимыми с другими аксиомами Евклида, – и отбросил этот вариант. Чтобы избавиться от варианта с острым углом, ему потребовалось намного больше времени, но в конечном итоге он вывел теоремы, противоречившие, по его мнению, остальным аксиомам. На самом деле это не так: если они чему-то и противоречат, то Евклидовой геометрии, аксиоме о параллельных и прочему. Так что Саккери думал, что доказал аксиому о параллельных, а мы сегодня считаем его работу большим шагом к логически непротиворечивым неевклидовым геометриям.

Отец Лобачевского, Иван, был мелким чиновником в учреждении, занимавшемся геодезической съемкой. Его мать Прасковья, как и отец, была родом из Польши. Отец Николая умер, когда мальчику было семь лет, и мать с детьми переехала в Казань. После окончания школы Николай в 1807 г. поступил в Казанский университет. Начал он с изучения медицины, но вскоре переключился на математику и физику. Среди его профессоров был друг Гаусса и бывший школьный учитель Бартельс.

В 1811 г. Лобачевский получил степень магистра математики и физики; он стал преподавателем, затем экстраординарным профессором, а к 1822 г. и полным профессором. Университетом в тот момент руководили консерваторы и ретрограды, опасавшиеся всего нового, особенно в естественных науках и философии. Они считали то и другое своего рода опасными следствиями Французской революции и угрозой православию – господствующей религии в России того времени. В результате академическая жизнь застопорилась, лучшие преподаватели (среди них и Бартельс) уехали, многих уволили; научные стандарты заметно снизились. Это было не лучшее место для человека, которому предстояло разрушить косную традицию в геометрии, насчитывавшую не одну тысячу лет; к тому же откровенность и независимость отнюдь не облегчали Лобачевскому жизнь. Тем не менее он продолжал математические исследования, и читаемые им курсы были образцом ясности и логичности изложения.

Административная карьера Лобачевского началась со вступления в университетскую комиссию по содержанию зданий и развивалась вполне успешно. Он приобретал новое оборудование для физической лаборатории и книги для библиотеки; руководил обсерваторией, был деканом физико-математического факультета с 1820 по 1825 г., заведовал библиотекой с 1825 по 1835 г. Его разногласия с властями сгладились, когда на престол взошел Николай I, который спокойнее относился к политике и управлению. Царь снял попечителя (формального главу) университета Михаила Магницкого с должности. Пришедший ему на смену Михаил Мусин-Пушкин стал надежным союзником Лобачевского, и в 1827 г. тот был назначен ректором университета. Назначение оказалось очень успешным; Лобачевский проработал на этом посту 13 лет, и за это время университет обзавелся новыми зданиями – библиотекой, а также корпусом для занятий астрономией, медициной и физикой. Он поощрял исследования в области изящных искусств и физики, увеличивал число студентов. Благодаря его быстрым и решительным действиям удалось минимизировать ущерб от эпидемии холеры в 1830 г. и пожара в 1842 г.; царь прислал Лобачевскому благодарственное письмо. Все это время он не переставал читать лекции по математическому анализу и физике, а также публичные лекции на разные темы.

В 1832 г., в возрасте 40 лет, Лобачевский женился на состоятельной девушке много младше себя – Варваре Алексеевне Моисеевой. За этот период он опубликовал две работы по неевклидовой геометрии: статью о «воображаемой геометрии» в 1837 г. и конспективное изложение теории на немецком языке, которое вышло в 1840 г. и произвело большое впечатление на Гаусса. У Лобачевских было 18 детей, из которых выжили семеро. Семья владела роскошным домом и вела активную социальную жизнь. В результате к моменту отставки Николай остался практически без денег, да и брак расстроился. Его здоровье ухудшилось, и в 1846 г. университет избавился от Лобачевского, назвав это событие «отставкой». Вскоре после этого умер его старший сын, а сам он начал терять зрение; постепенно он совсем ослеп и потерял способность ходить. Лобачевский умер в 1856 г. в бедности; он так и не узнал, что кто-нибудь когда-нибудь обратит внимание на открытую им неевклидову геометрию.

В этом большом прорыве в равной степени участвовал еще один математик – Янош Бойяи. Его идеи вышли в печатном виде в 1832 г. как приложение к «Эссе для любознательных юношей с рассказом об элементах математики» его отца Фаркаша Бойяи (свои статьи, издававшиеся на немецком языке, он подписывал «Вольфганг Бойяи»); называлось оно «Приложение, содержащее науку о пространстве, абсолютно истинную, не зависящую от истинности или ложности XI аксиомы Евклида (что a priori никогда решено быть не может)». Как правило, львиную долю заслуг в превращении неевклидовой геометрии в значительную область математики приписывают Бойяи и Лобачевскому, но предыстория вопроса включает еще четырех ученых, которые либо отказывались публиковать свои идеи, либо публиковали их, но не встречали понимания.

Фердинанд Швейкарт исследовал «астральную геометрию», развивая случай с острыми углами из работы Саккери. Он отослал рукопись Гауссу, но так и не опубликовал ее. Он посоветовал своему племяннику Францу Тауринусу продолжить эту работу, и в 1825 г. Тауринус опубликовал «Теорию параллельных прямых». В его «Первых элементах геометрии» 1826 г. утверждается, что случай тупых углов тоже приводит к разумной неевклидовой «логарифмически-сферической» геометрии. Работа не привлекла никакого внимания, и автор в отчаянии сжег оставшиеся экземпляры. Один из учеников Гаусса Фридрих Вахтер тоже писал про аксиому о параллельных – и тоже не был замечен.

Чтобы дополнительно запутать всю эту историю, Гаусс первым, еще в 1800 г., понял, что проблема аксиомы о параллельных связана не с реальным пространством, а с внутренней логикой Евклидовой геометрии. Линии, начерченные по линейке на листе бумаги, не в состоянии прояснить ответ. Может быть, если бы вы взяли достаточно большой лист бумаги, они встретились бы через миллион километров. А может быть, если вы построите множество точек, равноудаленных от какой-то определенной прямой, то результирующая линия окажется не прямой. Разбираясь с этой возможностью, Гаусс, вполне может быть, надеялся, подобно Саккери, получить в конечном итоге противоречие. Вместо этого он получил растущее число элегантных, убедительных, взаимно непротиворечивых теорем и к 1817 г. был убежден в возможности логически непротиворечивых геометрий, отличных от Евклидовой. Но он ничего не публиковал на эту тему, заметив в одном письме 1829 г., что «может пройти очень долгое время, прежде чем я опубликую свои исследования по этому вопросу: мало того, этого может и не произойти при моей жизни, ибо я опасаюсь “криков невежд”».

Вольфганг Бойяи, будучи старым другом Гаусса, написал великому математику с просьбой прокомментировать (положительно, как он надеялся) эпохальное исследование сына. Ответ Гаусса разрушил его надежды:

Все очень хорошо, но совершенно несправедливо, ведь Гаусс ничего по этому вопросу не публиковал. Конечно, отозваться с похвалой о радикальных идеях Яноша значило бы навлечь на свою голову «крики невежд». Похвалить в частном порядке, приватно, значило уклониться от ответа – и Бойяи-старший, и Гаусс это прекрасно понимали.

Лобачевский не знал, что по крайней мере два математика – Гаусс и Бойяи – уже занимались этой проблемой. Аксиома о параллельных подразумевает существование единственной прямой, параллельной к заданной и проходящей через заданную точку, и для начала он рассмотрел возможность того, что это утверждение ошибочно. Лобачевский заменил его утверждением о существовании множества таких прямых, чья «параллельность» означала, что прямые «не пересекаются, как бы далеко их ни продолжили». Он подробно проработал следствия из такого допущения. Он не доказал, что его геометрическая система логически непротиворечива, но не сумел и привести рассуждения к какому-нибудь противоречию; более того, убедился, что никакого противоречия здесь возникнуть не может. Мы сегодня называем его систему гиперболической геометрией, и она соответствует случаю острых углов Саккери. Тупые углы приводят к эллиптической геометрии, очень похожей на сферическую. Бойяи исследовал оба случая, тогда как Лобачевский ограничился только гиперболическим вариантом.

Потребовалось немало времени, чтобы математики осознали правомерность неевклидовой геометрии и постигли ее значение. Процесс признания начался с выхода из печати французского перевода работы Лобачевского, сделанного Жюлем Оуэлем в 1866 г., через 10 лет после смерти автора. В глаза пытливому читателю бросалась одна важная вещь: отсутствие доказательства того, что отрицание аксиомы о параллельных никогда не приведет к противоречию. Понимание пришло несколько позже: на самом деле существует три непротиворечивые геометрии, удовлетворяющие всем остальным аксиомам Евклида. Во-первых, это сама Евклидова геометрия; во-вторых, это эллиптическая геометрия, где параллельные прямые попросту не существуют; и в-третьих, это гиперболическая геометрия, где параллельные прямые существуют, но не единственны.

Доказательство непротиворечивости оказалось проще, чем можно было ожидать. Неевклидова геометрия может быть реализована как естественная геометрия поверхности постоянной кривизны: положительной для эллиптической геометрии, отрицательной – для гиперболической. Евклидова геометрия представляет собой переходный случай нулевой кривизны. Здесь «прямая» интерпретируется в «геодезическом» смысле, как кратчайшее расстояние между двумя точками. В такой интерпретации все аксиомы Евклида, кроме аксиомы о параллельных, могут быть доказаны при помощи Евклидовой геометрии. Если бы в эллиптической или гиперболической геометрии имелась хоть одна логическая нестыковка, ее можно было бы непосредственно перевести в соответствующую логическую нестыковку в Евклидовой геометрии поверхностей. Но если Евклидова геометрия непротиворечива, то непротиворечивы и эллиптическая, и гиперболическая геометрии.

В 1868 г. Эудженио Бельтрами предложил конкретную модель гиперболической геометрии: внутренняя геометрия поверхности, известной как псевдосфера и имеющей постоянную отрицательную кривизну. Он интерпретировал этот результат как наглядное подтверждение того, что на самом деле гиперболическая геометрия не есть нечто новое; это просто Евклидова геометрия, приспособленная к соответствующей поверхности. При этом он упустил из виду более глубокий логический вывод: эта модель доказывает непротиворечивость гиперболической геометрии, так что аксиома о параллельных не может быть выведена из других аксиом Евклида. Оуэль понял это в 1870 г., когда перевел статью Бельтрами на французский.

Подобрать модель для эллиптической геометрии было проще. По существу, это геометрия больших окружностей на сфере, с одной оговоркой. Большие окружности пересекаются в двух диаметрально противоположных точках, а не в одной точке, и потому не удовлетворяют остальным аксиомам Евклида. Чтобы исправить ситуацию, достаточно переопределить «точку» как «пару диаметрально противоположных точек» и рассматривать большую окружность как пару диаметрально противоположных полуокружностей. Это пространство – формально сфера с попарно отождествленными противоположными точками – обладает постоянной положительной кривизной, унаследованной от сферы.

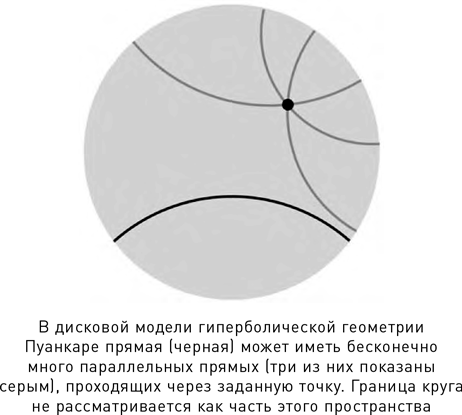
Тем временем неевклидова геометрия начала потихоньку появляться и в других областях математики, в первую очередь в комплексном анализе, где она связана с преобразованием Мёбиуса, отображающим окружности (и прямые) на окружности (и прямые). Вейерштрасс прочел лекцию на эту тему в 1870 г. Клейн, двигавшийся в том же направлении, уловил суть и обсудил эту идею с Софусом Ли. В 1872 г. он составил важный документ – Эрлангенскую программу, в которой определил геометрию как науку об инвариантах групп преобразований. Такой подход объединил почти все варианты, на которые успела разделиться к тому времени геометрия; основным исключением из этого перечня стала Риманова геометрия для поверхностей непостоянной кривизны, где подходящих групп преобразований просто нет. Пуанкаре зашел еще дальше, предложив, в частности, собственную модель гиперболической геометрии. Пространство в ней представляет собой внутренность круга, а «прямые» линии – дуги окружностей, подходящих к границе круга под прямыми углами.

Позже гиперболическая геометрия стала одним из стимулов к появлению Римановой теории искривленных пространств любой размерности (многообразий), на которой построена теория гравитации Эйнштейна (глава 15). В число ее приложений в современной математике входят комплексный анализ, специальная теория относительности, комбинаторная теория групп и гипотеза (теперь уже теорема) о геометризации Тёрстона в топологии трехмерных многообразий (глава 25).