5.4. Всеобъемлющий процесс ценообразования

Назад: 5.3. Жесткие процессы ценообразования

Всеобъемлющие процессы ценообразования принимают в расчет данные и по рынкам, и по затратам. Эти процессы включают в себя расчеты контрибуционной маржи, дерева решений, системы поддержки принятия решений и маржинальный анализ. В рамках данных процессов осуществляются сравнение и оценка альтернативных цен [1]. Хотя расчеты контрибуционной маржи и дерево решений рассматривают только несколько ценовых пунктов, системы поддержки принятия решений могут охватывать большее количество пунктов. Маржинальный анализ укрупняет неограниченное количество ценовых пунктов, представляя их в виде уравнения и обеспечивая очень тщательную оценку возможных ценовых пунктов.

Односторонние, жесткие и гибко-интуитивные процессы имеют одно общее ограничение: они не устанавливают взаимосвязи между ценой и определяющими ее факторами [1]. В одностороннем жестком процессе цена является функцией издержек или конкурентных цен, то есть определяется издержками или конкуренцией. Во всеобъемлющем процессе все факторы, влияющие на цену, сами по себе являются функциями цены. Это значит, что затраты, спрос и цены конкурентов (как показано на рис. 1.7) следует считать ценозависимыми. По логике, это единственный корректный процесс принятия решений. Принимая такие решения, необходимо учитывать все переменные, в зависимости от типа решения.

5.4.1. Анализ безубыточности

Анализ безубыточности обрабатывает данные о затратах и объемах продаж и включает в себя оценку различных ценовых альтернатив. Теоретически он требует строго разделить постоянные и переменные компоненты затрат [8, 9]. Постоянные затраты рассматриваются единым блоком. Не завися по определению от любых решений в рамках конкретного планового периода, постоянные затраты не должны влиять на ценовое решение до его окончания. Здесь упор делается на контрибуционную маржу прибыли. Безубыточный объем продаж или максимальная совокупная контрибуционная маржа служат критериями ценового решения.

Стадии безубыточного анализа следующие.

1. Выбор потенциальной цены.

2. Расчет удельной контрибуционной маржи путем вычета переменных удельных затрат k из цены p. В безубыточном анализе принята линейная функция затрат, поэтому переменные удельные затраты и маржинальные затраты являются постоянными и идентичными. Уравнение удельной контрибуционной маржи:

d = p – k

3. Расчет безубыточного объема q_BE путем деления постоянных затрат Cfix на удельную контрибуционную маржу d:

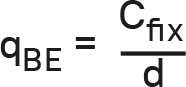
Показатель объема в точности покрывает постоянные затраты, прибыль равна нулю. Таким образом, безубыточный объем также соотносится с пороговым значением прибыльности.

4. Оценка возможности выйти за объем безубыточности при выбранной цене. Если ожидаемый объем продаж превышает объем безубыточности, это означает, что продукт приносит прибыль. Если предполагаемый объем меньше объема безубыточности, продукт принесет убыток.

Четвертая стадия неявно подразумевает существование и применение функции «цена-отклик», поскольку необходимо определить, каким будет объем продаж при конкретной цене.

Если стадии с первой по четвертую пройдены при всего одном варианте цены, результат можно использовать только для решения «да-нет» о том, предлагать ли продукт по такой цене. Чтобы применять анализ безубыточности для ценовых решений, нужно выполнить стадии 1–4 для нескольких ценовых вариантов. На четвертой стадии нужно оценить, какой цене соответствует наивысшая вероятность достижения или превышения порога безубыточности.

В табл. 5.3 данный подход представлен в виде простого примера с переменными удельными затратами $5 и постоянными затратами $100 000. Значения объемов безубыточности даны для пяти ценовых вариантов.

Таблица 5.3. Объемы безубыточности для альтернативных цен

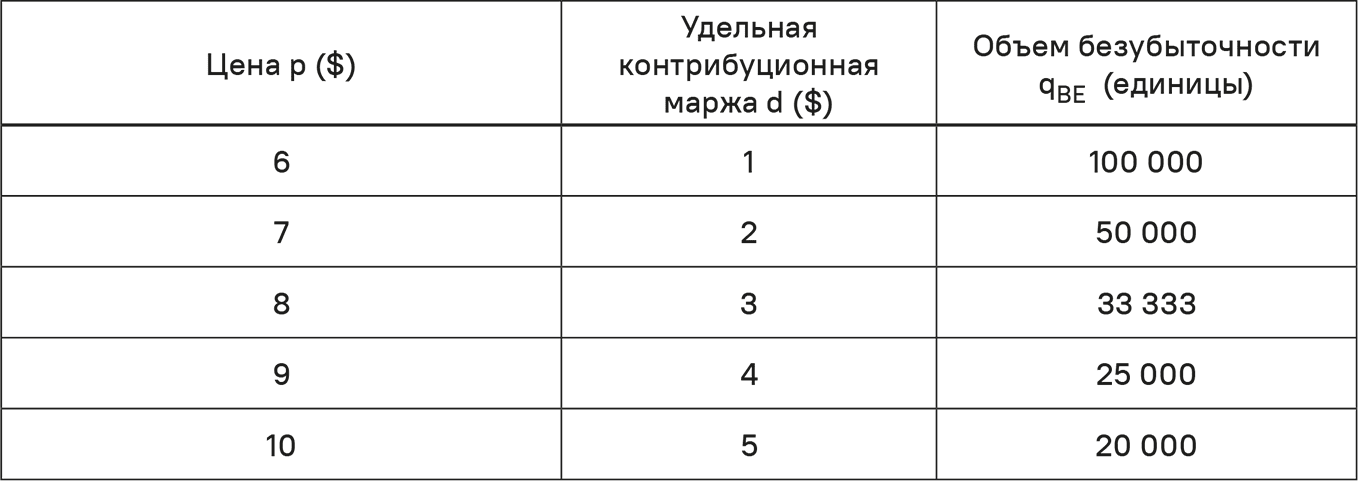
На рис. 5.1 эта взаимосвязь показана графически. По мере роста цены объем безубыточности снижается по экспоненте. Не следует, однако, делать отсюда вывод, что легче добиться низких объемов безубыточности. Они ассоциируются с высокими ценами, которые, как правило, снижают объемы.

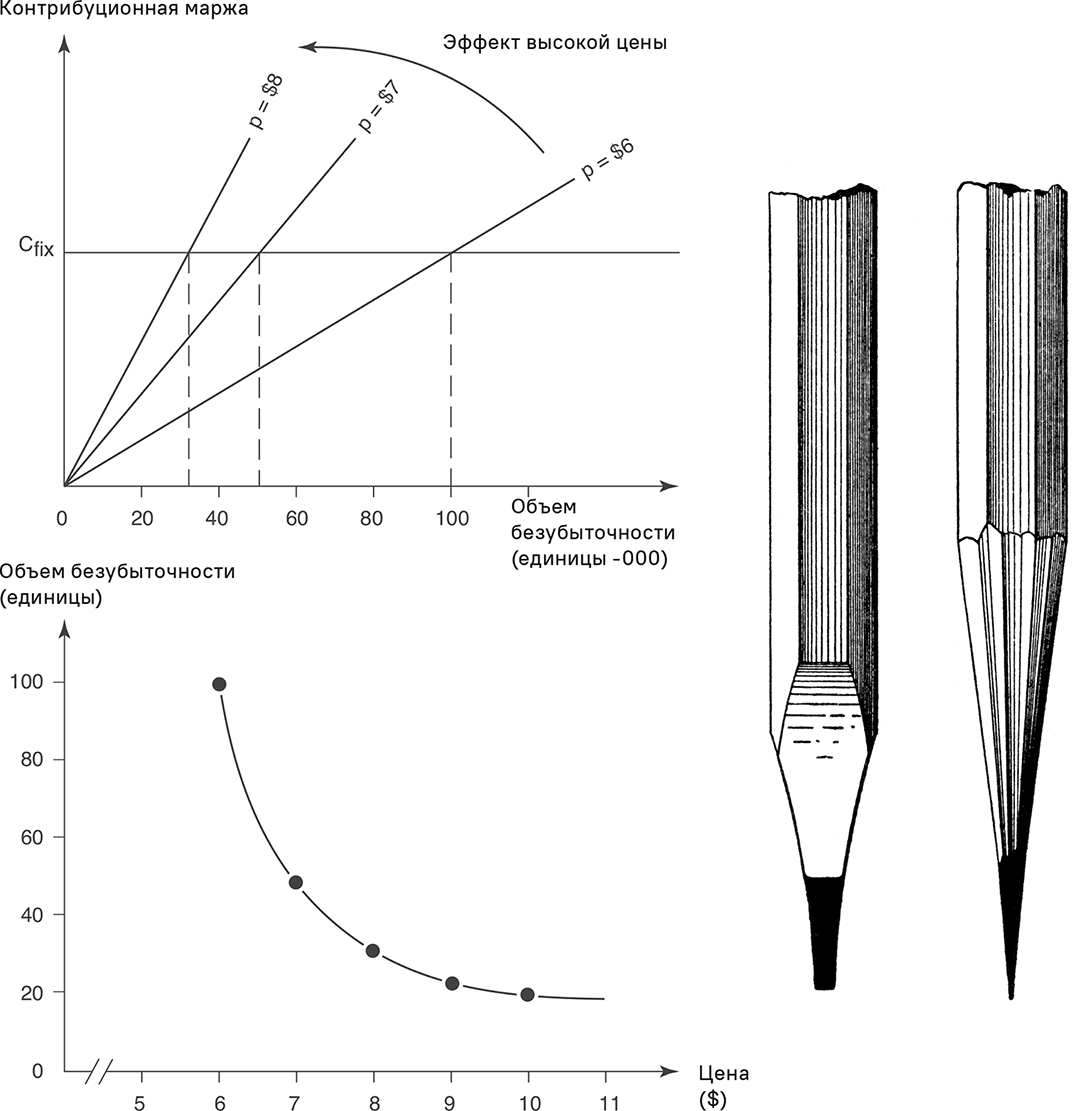
Рис. 5.1. Отношение между объемами безубыточности и ценой

Руководство компании обязано определить, какое сочетание цены и объема безубыточности окажется наилучшим. Анализ безубыточности в поддержку принятия ценовых решений имеет смысл только в том случае, если вероятности выхода на альтернативные уровни объема безубыточности значительно различаются. Зачастую вероятности достижения и превышения разных объемов безубыточности (при разных ценах) одинаковы.

Иными словами, критерий безубыточности значительно не различается. Объем безубыточности как критерий неполон, поскольку не принимает в расчет того, что происходит за точкой безубыточности. Несмотря на это, анализ безубыточности является практическим инструментом принятия решений «да-нет» при вводе продукта на рынок, сохранении его в ассортименте или отказе от него. Несколько меньше он подходит для ценообразующих решений.

Ту же процедуру можно использовать для решения об изменениях цены. На рис. 5.2 представлен простой пример снижения/повышения цены. Мы видим изменение цены и требуемое изменение объема продаж. На горизонтальной оси показаны переменные удельные затраты в процентах от текущей цены. На вертикальной оси показано необходимое увеличение объема продаж (вверх) и приемлемое снижение объемов (вниз) для выхода на аналогичную прибыль. Мы рассмотрим изменения цены на 10 и 20 %.

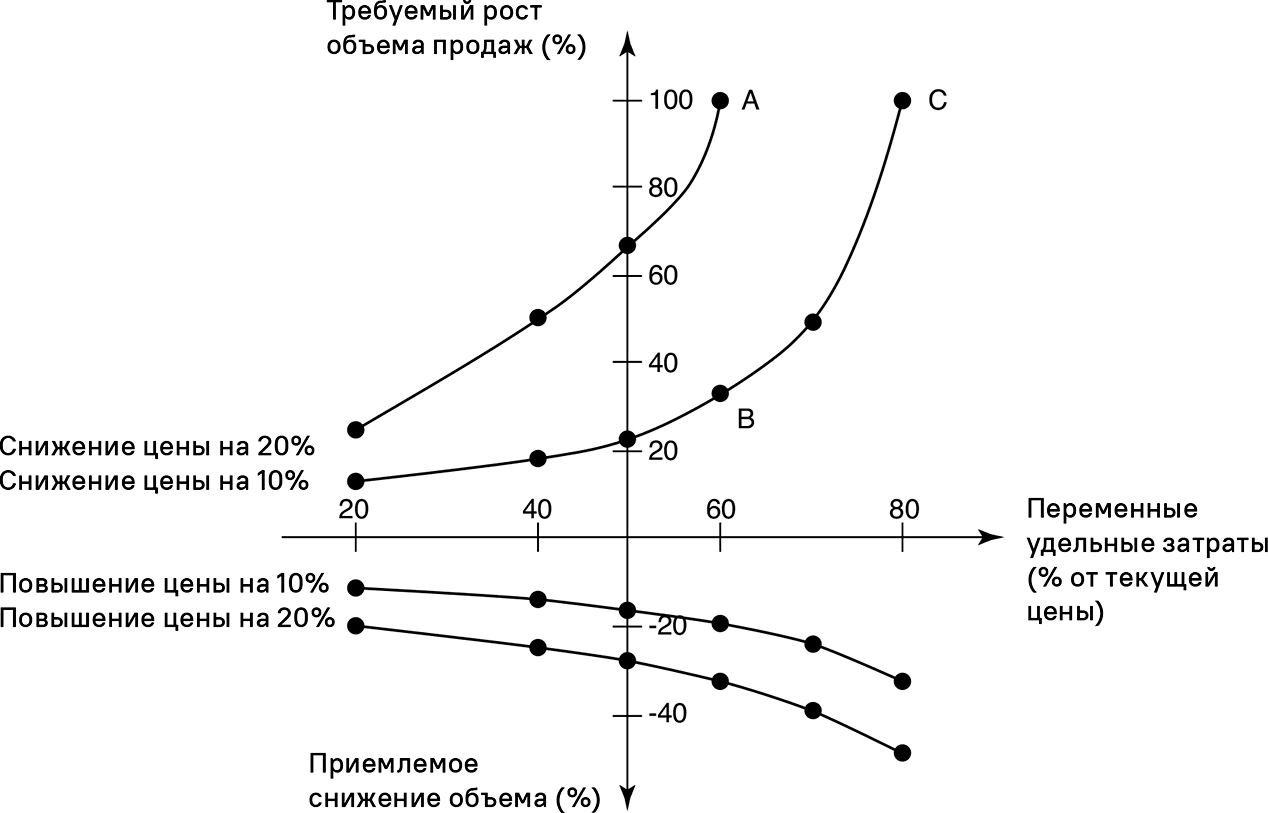
Рис. 5.2. Кривые одинакового уровня прибыльности

Давайте сначала рассмотрим кривые снижения цены в верхней части графика. Кривая снижения цен на 20 % показывает: когда переменные удельные затраты составляют 60 % от текущей цены, необходимое повышение объема для поддержания постоянного уровня прибыли 100 % (точка A). Если цена снижается всего на 10 %, требуемое повышение объема 33 % (точка B). Данный численный пример проясняет, насколько чувствительна прибыль к изменениям цены при относительно высоких переменных удельных затратах. Чем выше переменные удельные затраты, тем круче кривая. Если переменные удельные затраты составляют 80 % от текущей цены, необходимо повысить объемы на 100 %, чтобы нивелировать снижение цены на 10 % и поддержать уровень прибыли (точка C).

Напротив, кривые повышения цен на 10 и 20 % в нижней части рис. 5.2 более плоские и приближены друг к другу. Это доказывает, что приемлемые уровни снижения объемов продаж менее чувствительны к процентной доле переменных удельных затрат. Подобные цифры хорошо помогают в принятии решений при оценке ценовых изменений. Они ясно показывают, как нужно изменить объем продаж, чтобы обеспечить постоянную прибыль.

Максимизация контрибуционной маржи

При установлении цен лучше делать упор на общую ожидаемую контрибуционную маржу, чем ориентироваться исключительно на объем безубыточности. Поскольку постоянные затраты являются константой, цена, обеспечивающая самую высокую контрибуционную маржу, одновременно обеспечивает и максимальную прибыль. Максимизация контрибуционной маржи сходна с максимизацией прибыли. Для расчета контрибуционной маржи существует обязательное условие: необходимо определить ценовые альтернативы и иметь возможность спрогнозировать для них объем продаж. Иными словами, необходимо напрямую учитывать влияние цены на объем. Данный подход отображен на рис. 5.3.

Максимизация контрибуционной маржи является логически обоснованным методом ценовой оптимизации. Одно из его достоинств – простота. Здесь не требуется ни уравнений, ни усложненных математических методов оптимизации. Нужно только рассчитать значения контрибуционной маржи для небольшого количества альтернативных цен, а затем сравнить их. Сам процесс поэтому весьма практичен. Он, безусловно, превосходит метод принятия решений «издержки плюс».

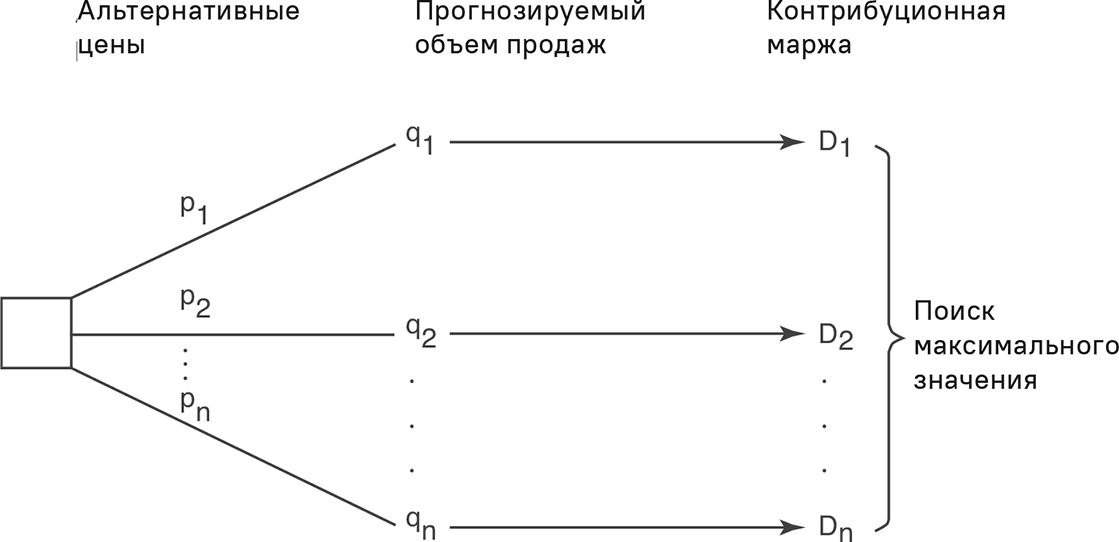
Рис. 5.3. Максимизация контрибуционной маржи

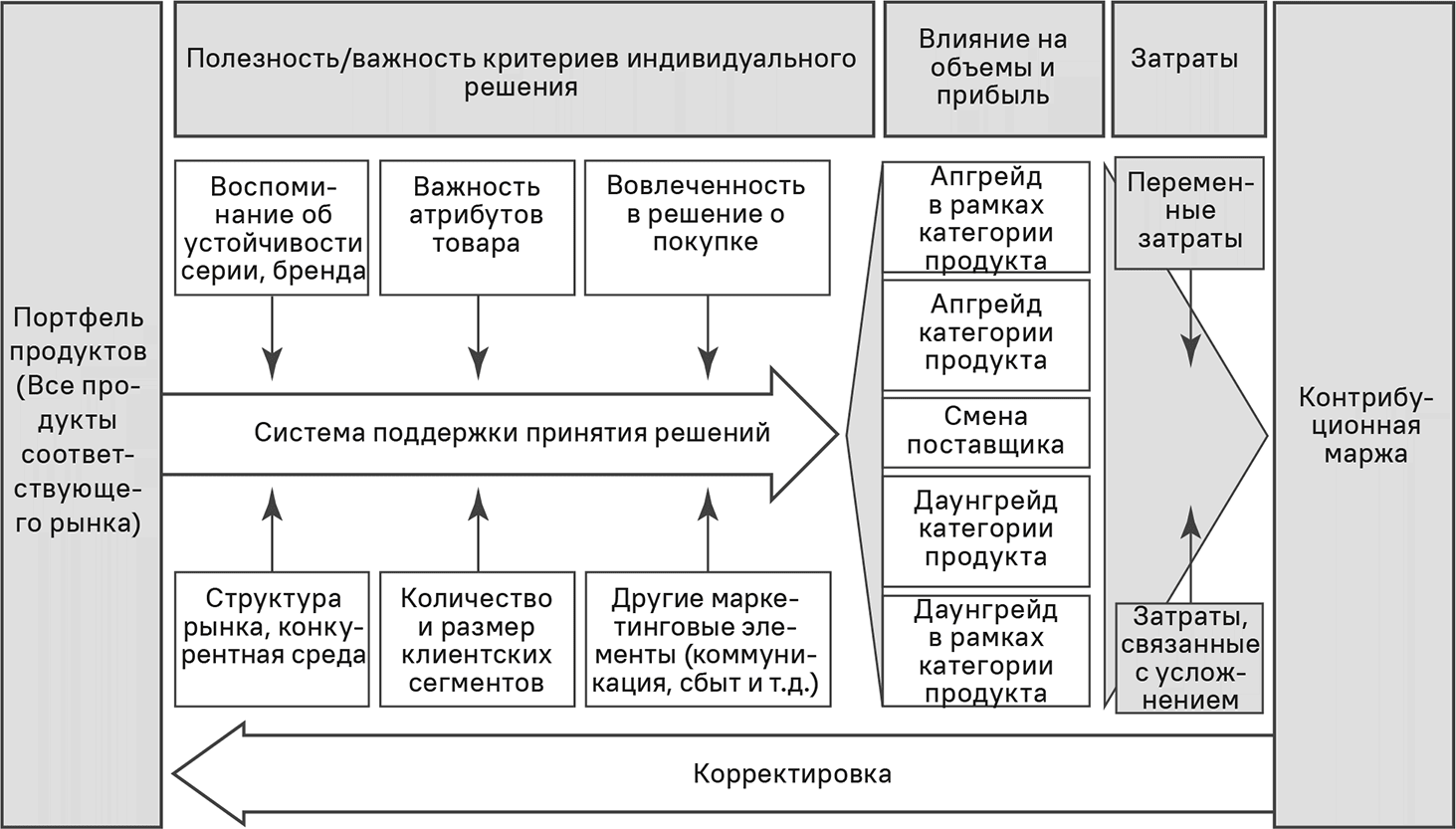
Рис. 5.4. Структура системы принятия решений

5.4.2. Системы поддержки принятия решений

До сих пор мы рассматривали методы, которые не всегда отвечают сложности ценовых решений в реальной жизни. Возможно, здесь более подходят комплексные системы поддержки принятия решений.

Системы поддержки принятия решений основаны на интегрированной обработке информации о потребительских предпочтениях и потребностях, решении о покупке, рыночной структуре и тенденциях (как для собственных товаров, так и для продукции конкурентов), а также других маркетинговых инструментах (коммуникации, продажах и сбыте). Эта информация, как показано на рис. 5.4, обобщается в системе поддержки принятия решений, позволяя прогнозировать объемы продаж при различных ценах. Здесь можно учитывать большой набор ценовых эффектов: движение потребителей между поставщиками, категориями товаров одного поставщика и в рамках одной категории товара. Если включить в систему издержки, можно рассчитывать прибыли.

Чтобы система поддержки принятия решений отражала реальное решение о покупке, следует учитывать несколько факторов влияния.

• Прежде всего, необходимо в точности определить соответствующий рынок. Если это рынок автомобилей, то там предлагаются только модели класса «премиум» или бюджетные модели тоже? Решения о будущих товарах затрагивают только частных клиентов/потребителей или влияют также на решения о покупке деловых клиентов? От определения соответствующего рынка зависит, какие товары (собственные и конкурентные) будут включены в систему.

• Главные элементы системы поддержки принятия решений – это клиентские предпочтения и потребности, а также процессы принятия решений о покупке. Информация по этим двум аспектам собирается в ходе опросов потребителей.

• Процессы принятия решений о покупке различаются в зависимости от продукта и ситуации. Процесс для продуктов с низкой вовлеченностью отличается от процесса для продуктов с высокой вовлеченностью [10].

• Последний этап разработки системы поддержки принятия решений – это корректировка. Корректируется прогноз доли рынка, сделанный исходя из собранных данных и базовых алгоритмов, чтобы он возможно лучше отражал действительность. Такие корректировки делаются вручную. Итоговые доли рынка формируют базовый сценарий, который используется в дальнейшем моделировании. Это напоминает процесс, принятый в метеорологии, где происходит корректировка сложных моделей прогнозирования погоды с использованием ретроспективных данных, а затем дается прогноз на будущее [11].

В итоге необходимо как можно реалистичнее смоделировать индивидуальный контекст принятия решения клиентом и функцию «цена-отклик». Здесь требуется глубокое понимание релевантных характеристик на уровне индивидуального потребителя. Степень детализации выводов и результатов системы поддержки принятия решений зависит от формулировки вопросов, на которые нужно получить ответ.

Пример: Система поддержки принятия решений для инновации

При запуске нового продукта компании сталкиваются с большой неопределенностью, связанной с оптимальными ценами. Это особенно проявляется в случае инноваций, формирующих новые рынки. Ошибки изначального позиционирования исправлять сложно. В таких ситуациях пользу приносят системы поддержки принятия решений, которые квантифицируют влияние различных ценовых уровней на продажи и прибыли. На рис. 5.5 представлен случай инновационного профессионального устройства для глажения рубашек. В левой части рисунка изображено гладильное устройство и показана спецификация продукта и цена базовой конфигурации. Справа изображены кривые «цена-отклик» для трех вариантов продукта, выведенные с помощью системы поддержки принятия решений. Если включить затраты по разным вариантам, можно рассчитать соответствующую прибыль. Исходя из этого, можно принимать фундаментальные ценовые решения с учетом стратегических целей (целевые объемы и прибыли). Критическими факторами успешности системы поддержки принятия решения являются точное определение потребительской ценности отдельных атрибутов и цен продукта, а также квантификация рыночного потенциала.

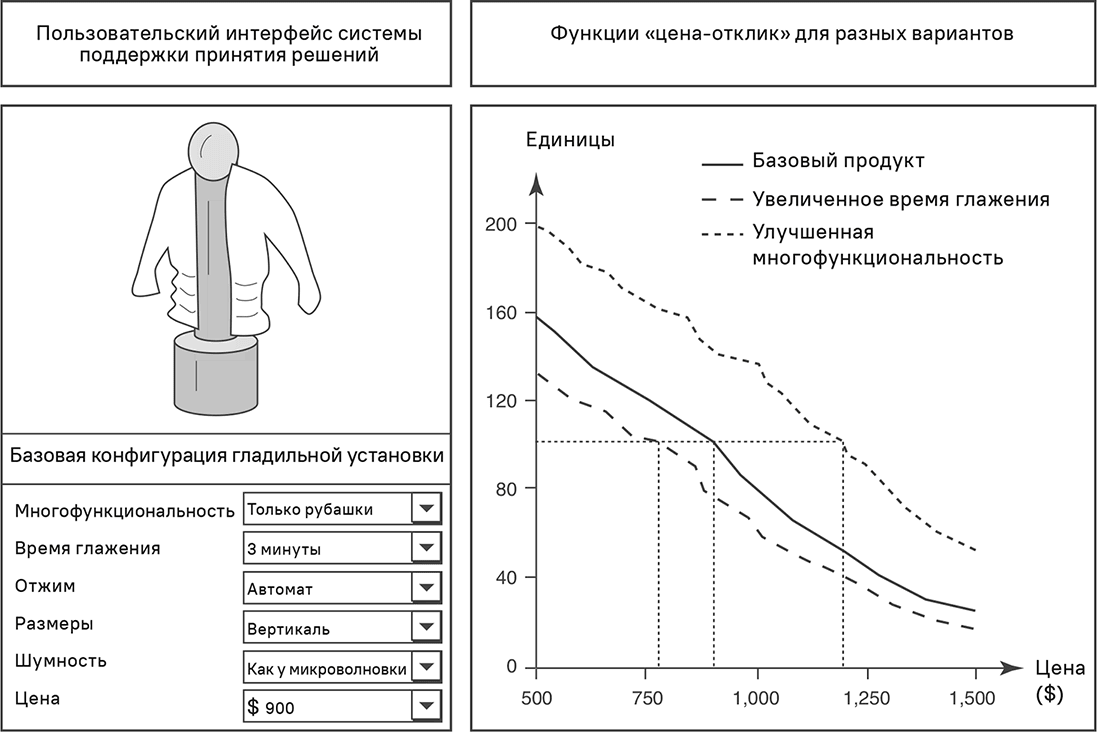
Рис. 5.5. Пользовательский интерфейс и функции «цена-отклик» системы поддержки принятия решений для гладильной установки

Обзор

Обобщим выводы о применении систем поддержки принятия решений.

• Системы поддержки принятия решений отлично приспособлены для поддержки принятия комплексных ценовых решений.

• Особую важность представляют два аспекта: (1) адаптация модели к конкретной ситуации и ее корректировка; (2) тщательная методологическая экспертиза. Стандартизированные модели, применяемые без глубокого понимания методологии и системных взаимозависимостей, существенно повышают риск ошибок.

• Чтобы добиться достоверных и надежных результатов, рекомендуем комплексное использование различных источников информации и аналитических методов.

5.4.3. Математическая оптимизация цен

Самая элегантная и точная форма ценовой оптимизации – математическая. Она определяет цену максимизации прибыли путем выражения отношений «цена-объемы» в виде математических функций. Здесь берутся в расчет все цены в определенных интервалах, а не только небольшое количество выбранных ценовых пунктов.

Оптимальная цена определяется не сравнением дискретных значений, а исследованием всей кривой прибыльности. Таким образом, можно вывести простые правила оптимальности для конкретных функций «цена-отклик» и затратности.

5.4.3.1. Монопольный рынок

Сначала рассмотрим случай компании-монополиста. Нам нет необходимости принимать в расчет цены конкурентов. Функция прибыльности выглядит так:

π = R – C = p × q(p) – C[q(p)],

где R – доход; С – затраты; p – цена; q – количество; q(p) – функция «цена-отклик». Для максимизации прибыли дифференцируем функцию прибыльности и получим:

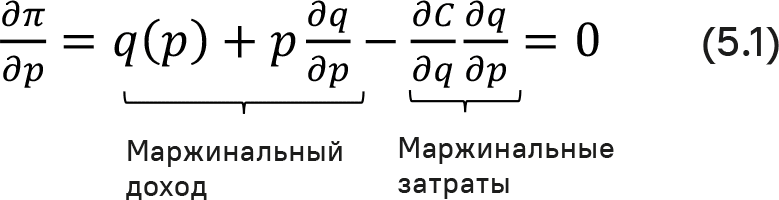
При оптимальной цене p* данная производная равна нулю. Это случай, когда маржинальный доход и маржинальные затраты (как функция цены) равны. Условие «маржинальный доход = маржинальные затраты» требует сбалансированного изменения дохода и затрат. Если цена ниже оптимального значения, затраты будут расти быстрее дохода. Напротив, если цены выше оптимальной, доход будет расти быстрее затрат. В любом случае прибыль будет ниже оптимальной цены p*.

Можно объяснить эффекты отклонения цены от оптимума с точки зрения удельной контрибуционной маржи и объема, которые двигаются в противоположных направлениях, как и изменения цены.

• Цена растет от оптимального значения.

Повышение цены относительно оптимального значения дает повышение удельной контрибуционной маржи. Процентный прирост удельной контрибуционной маржи, однако, ниже процентного снижения объемов продаж. Это вызывает чистый отрицательный эффект для прибыли.

• Цена снижается от оптимального значения.

Снижение цены от оптимального значения приводит к повышению объема продаж, однако процентный прирост объема меньше процентного снижения удельной контрибуционной маржи. Это также вызывает чистый отрицательный эффект для прибыли.

Условие (5.1) также предполагает, что на оптимальную цену влияют только маржинальные затраты. Оптимальная цена не зависит от постоянных затрат. Если мы берем производное от функции прибыльности, постоянные затраты исчезают из уравнения, поскольку являются константой. Любой метод ценообразования, предполагающий установление оптимальной цены как функции постоянных издержек, логически некорректен.

Можно воспользоваться значениями ценовой эластичности и вывести простую формулу оптимальной цены p* [из формулы (5.1)], так называемую формулу Аморозо – Робинсона:

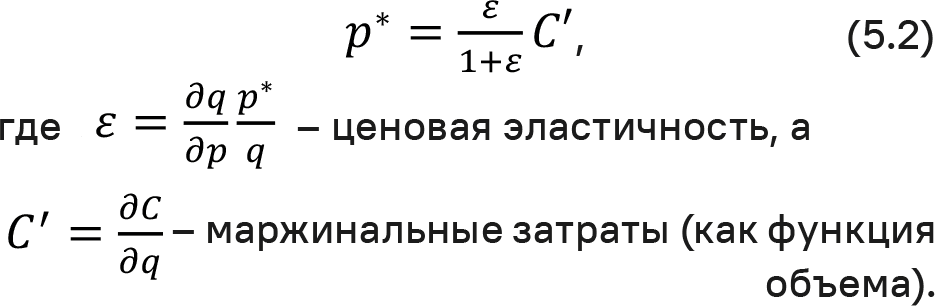
Таким образом, оптимальная цена – это основанная на эластичности надбавка к маржинальным затратам. Однако уравнение (5.2) не решает проблему установления оптимальной цены p*. Это, скорее, переформулирование необходимого условия «маржинальный доход = маржинальные затраты».

Ценовая эластичность и маржинальные затраты С’ сами по себе могут являться функцией цены. Чем выше ценовая эластичность (в абсолютных терминах), то есть чем чувствительнее спрос к ценовым изменениям, тем ниже оптимальная цена. Оптимальная цена всегда находится в диапазоне, для которого ценовая эластичность (в абсолютных терминах) больше 1.

Так как ценовая эластичность цены максимизации дохода равна –1, цена максимизации прибыли всегда выше цены максимизации дохода. Повышение цены увеличит прибыль, если ценовая эластичность меньше 1 в абсолютных терминах. Например, если повышение цены на 10 % дает снижение объемов на 5 %, ценовая эластичность равна –0,5. Значит, имеет смысл поднять цены.

5.4.3.2. Ценовая оптимизация для мультипликативной функции «цена-отклик»

Как нам известно из главы 3, функция «цена-отклик» имеет постоянную ценовую эластичность. Если маржинальные затраты также являются константой, то есть функция затрат линейная, можно использовать формулу (5.2) непосредственно как правило для ценовых решений. Если ценовая эластичность, например, имеет значение –2, оптимальный коэффициент надбавки равен 2. К маржинальным затратам добавляется значение 100 %. Если ценовая эластичность равна –3, коэффициент надбавки равен 1,5, что означает 50 %-ную надбавку к маржинальным затратам. Если ценовая эластичность равна –5, надбавка равна всего 25 %. Чем ближе ценовая эластичность к 1, тем выше коэффициент надбавки. При ценовой эластичности –1,2 надбавка равна 500 %.

5.4.3.3. Ценовая оптимизация для линейной функции «цена-отклик»

Для линейной функции «цена-отклик» и линейной функции затрат формула оптимальной цены выглядит так:

р* = 1/2 (a/b + k) (5.3)

Дробь a/b – это максимальная цена, то есть цена, при которой объем продаж равен нулю.

Оптимальная цена p* лежит точно посередине между переменными удельными затратами k и данной максимальной ценой. Чтобы определить оптимальную цену в случае линейности, нужно только знать переменные удельные затраты и максимальную цену.

Как следует из уравнения (5.3), рост затрат приведет к повышению цены на половину данного количества. Аналогичным образом всего половина снижения затрат перейдет клиентам. В действительности можно наблюдать, что компании не полностью отражают изменения затрат в ценах. Например, когда цены на молоко поднялись на 10 центов, ALDI переложила на потребителей только 7 центов [12]. Напротив, экономия затрат обычно напрямую переводится на клиентов, как указано на домашней странице ALDI Süd, одного из двух операционных подразделений компании [13]. (Другое подразделение, ALDI Nord, управляет сетью Trader Joe’s в США.)

В другом случае фирма клининга зданий переносит только 80 % повышения расходов на персонал на своих клиентов [14]. После падения цен на нефть CEO Ryanair Майкл О’Лири [15] заявил, что компания перенесет почти всю (но не всю) экономию на своих клиентов. «Почти всё» можно понимать так, что лишь часть экономии будет отражена в снижении цен на билеты – что ж, мудрый ход.

Теперь мы продемонстрируем ценовую оптимизацию линейных функций «цена-отклик» и затрат для модного бренда. Постоянные затраты составляют $2,95 млн. Переменные удельные затраты составляют $60. Функция «цена-отклик» выглядит так:

q = 300 000 – 2000p

следовательно, максимальная цена p^max = 300 000/2000 = $150.

Итак, оптимальная цена:

p* = 1/2 (150 + 60) = $105.

Рис. 5.6 выражает эту функцию в графическом виде. Цена $105 лежит в точности посередине между переменными удельными затратами $60 и максимальной ценой $150.

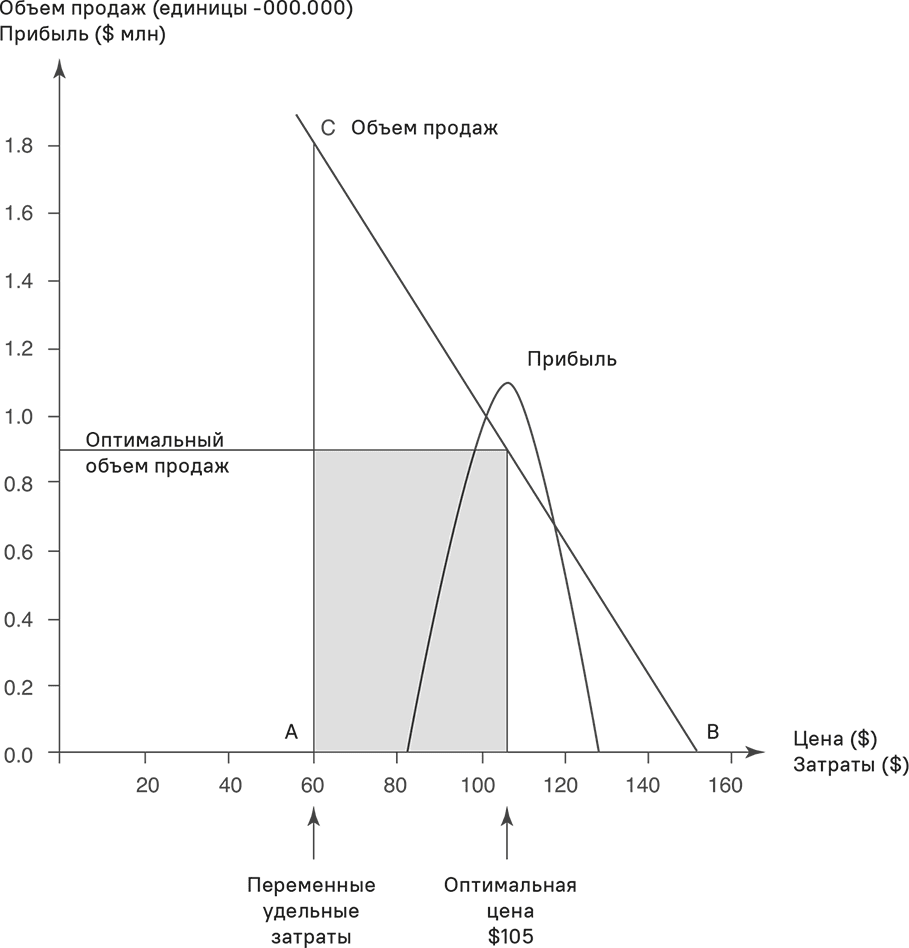
Рис. 5.6. Определение оптимальной цены (линейные функции «цена-отклик» и затрат)

Общая контрибуционная маржа, то есть сумма удельной контрибуционной маржи и объема продаж, графически выглядит как треугольник. Кривая прибыльности описывает размер треугольника. Область треугольника (то есть общая контрибуционная маржа) достигает максимума, когда цена попадает в срединную точку между переменными удельными затратами и максимальной ценой. Объем продаж при этой цене равняется 90 000 единиц. Максимальная прибыль равна $1,1 млн. Чем больше отклонение от цены максимизации прибыли, тем сильнее снижение прибыли. Кривая прибыльности симметрична. Это означает, что отклонение цены вверх от оптимума оказывает на прибыль такое же воздействие, как и отклонение вниз той же величины.

5.4.3.4. Ценовая оптимизация для функции Гутенберга

Гутенберговская функция «цена-отклик» (см. рис. 3.6) дает более сложные кривые прибыльности. Это может быть либо глобальный максимум, либо два локальных максимума. В каждой из этих точек выполняется общее условие «маржинальный доход = маржинальные затраты».

Таким образом, недостаточно знать только одну цену, при которой выполняется данное условие. Нужно найти глобальный максимум прибыли.

Различные случаи лучше всего проиллюстрировать численными примерами. Предполагаем, что существует следующая функция Гутенберга «цена-отклик»:

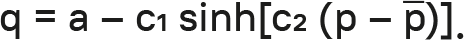
Переменная p представляет собой либо конкурентную цену (если мы смотрим на ценовую разницу с конкурентами), либо предыдущую цену (если смотрим на влияние ценового изменения).

В каждом примере устанавливаем a = 10 и p = 2. Возьмем линейную функцию затрат с переменными удельными затратами k. Есть три возможных варианта, как показано в табл. 5.4:

Таблица 5.4. Значения параметров для трех вариантов функции Гутенберга

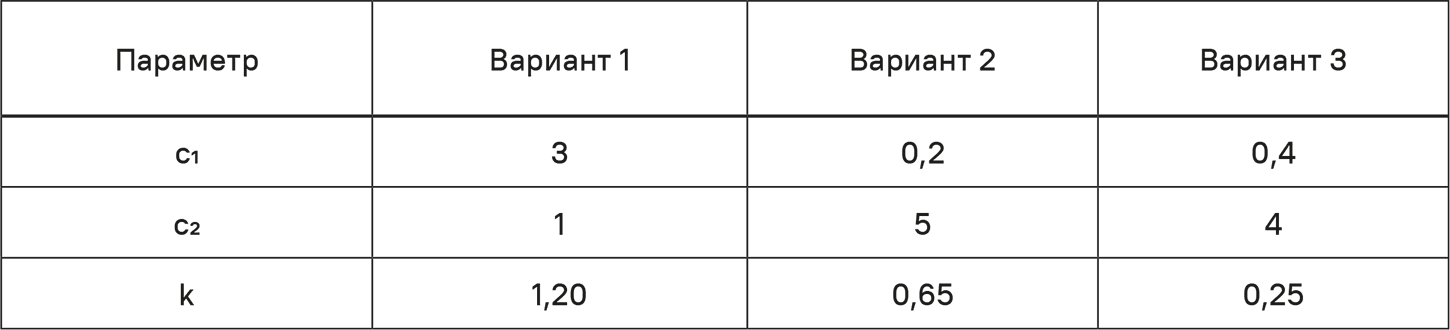
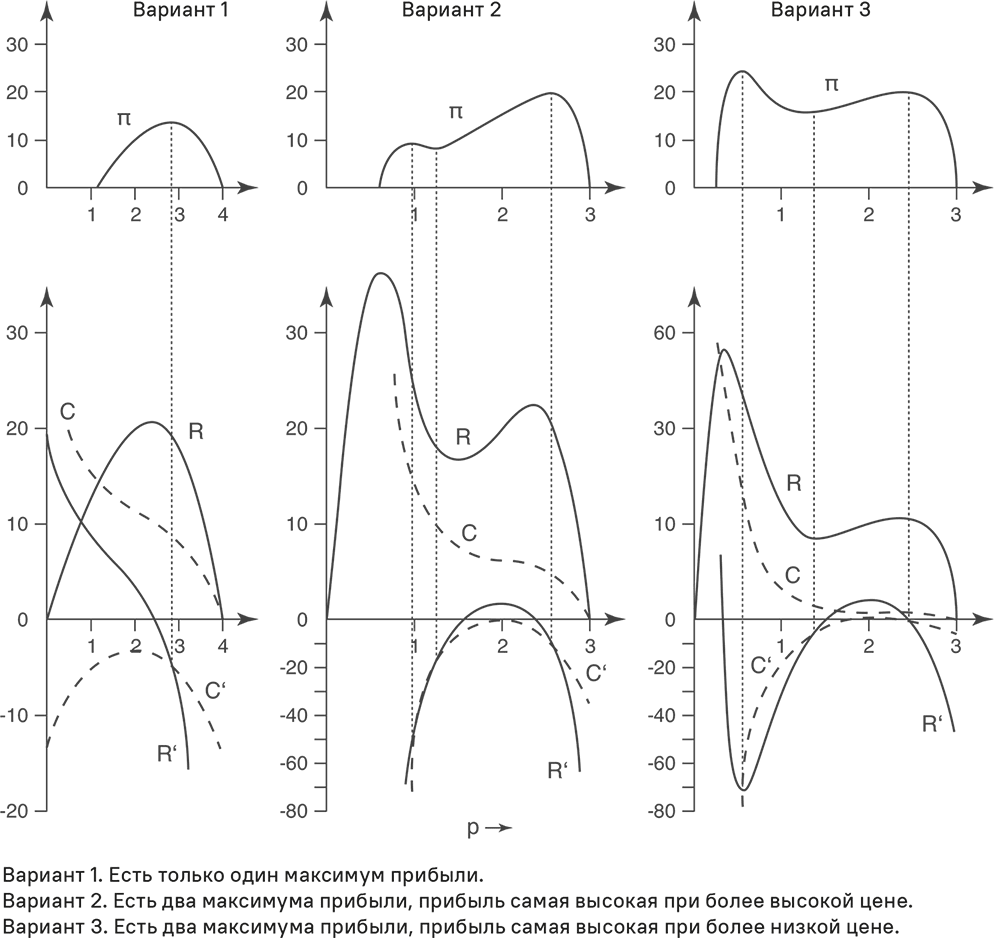
Рис. 5.7. Три варианта функции Гутенберга

На рис. 5.7 представлены три этих случая. В верхней части рисунка показаны функции прибыли, где можно распознать максимумы прибыли и оптимальные цены.

В нижней части поясняется, как были выведены эти кривые. С этой целью кривые, показанные сплошной линией, отражают прибыль R и маржинальный доход R'. Пунктирными линиями показаны затраты С и маржинальные затраты С'.

Таблица 5.5. Оптимальные значения для трех вариантов функции Гутенберга

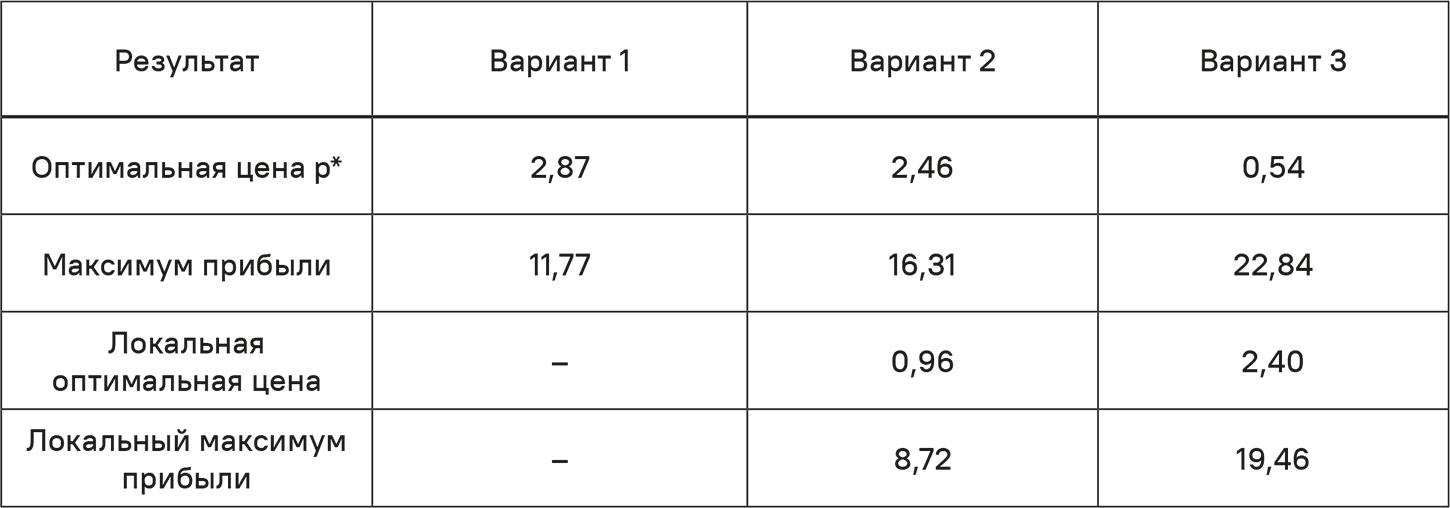
Тонкие вертикальные линии отмечают соответствующие позиции максимумов и минимумов функции прибыльности, которые всегда совпадают, если маржинальный доход равен маржинальным затратам, то есть там, где кривые пересекаются.

Вариант 1. Один максимум прибыли

Если функция Гутенберга имеет незначительный излом, тогда есть только один максимум прибыли. Снижение цен не вызывает достаточного спроса и, таким образом, сокращает прибыль. Оптимальная цена лежит в верхнем конце монополистической части функции Гутенберга.

Вариант 2. Два максимума прибыли. Оптимальна более высокая цена

Функция Гутенберга в этом случае имеет более сильный излом, так что есть второй максимум прибыли при низкой цене. Однако излом выражен недостаточно. Это означает, что увеличенные объемы продаж по сниженной цене не смогут компенсировать падение удельной контрибуционной маржи. Повышение прибыли дает более высокая цена. Оптимальная цена опять-таки лежит в верхнем конце монополистической части функции Гутенберга. Это указывает на позиционирование в премиальном сегменте.

Вариант 3. Два максимума прибыли. Оптимальна более низкая цена

Это случай, когда функция Гутенберга имеет выраженный излом. Объем продаж намного сильнее реагирует на крупные ценовые отклонения или снижения, чем на незначительные. Чем больше растет ценовая эластичность при снижении цены, тем выше вероятность варианта 3, а также того, что глобальный максимум прибыли будет достигнут при низкой цене. В этом случае оптимально низкоценовое позиционирование.

В табл. 5.5 представлен обзор оптимальных значений трех вариантов функции Гутенберга.

Функция затрат влияет на ценовое позиционирование. Постоянные или низкие маржинальные затраты или же затраты, сопровождающиеся падением объемов, благоприятствуют низкоценовому позиционированию, в то время как постоянные и высокие или неуклонно увеличивающиеся маржинальные затраты говорят в пользу позиционирования в премиальном сегменте цен.

Если обобщить влияние эффектов затрат и цен (последние попадают в категорию функций «цена-отклик» со слабым или сильным изломом), то можно сформулировать качественные рекомендации, представленные в табл. 5.6.

Таблица 5.6. Качественные рекомендации для различных вариантов функции Гутенберга и маржинальных затрат

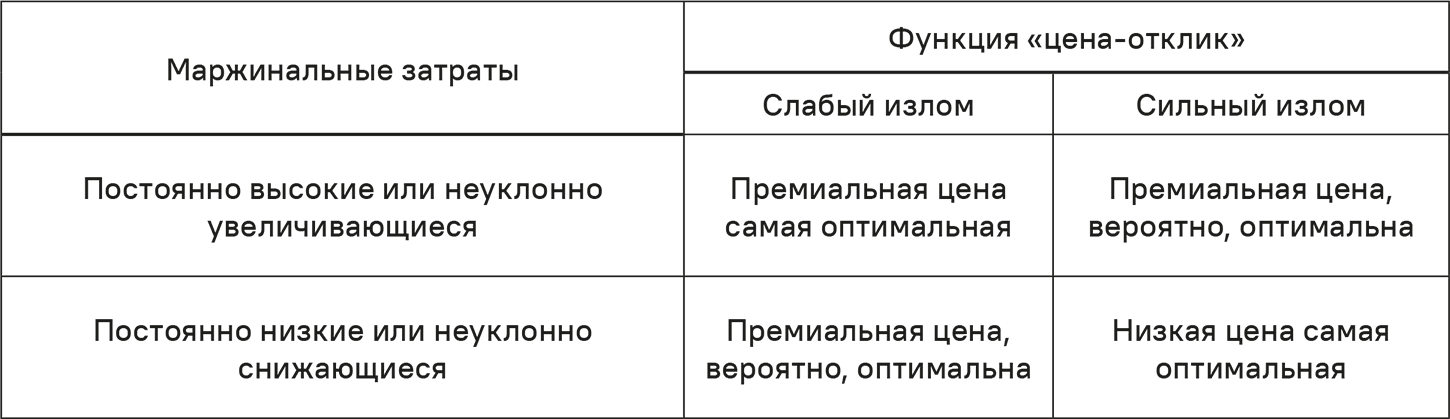
Обзор

Ниже мы обобщим выводы относительно ценового позиционирования с функцией Гутенберга «цена-отклик». Могут иметь место два локальных максимума прибыли. Первый находится в точке премиальной цены; второй, если он есть, находится в точке заметно более низкой цены. Непременными условиями максимума прибыли на низком ценовом уровне являются сильный излом функции «цена-отклик» и низкие маржинальные затраты. За счет потенциального наличия двух максимумов прибыли измерение и анализ функции «цена-отклик» должны охватывать большой ценовой диапазон. Если брать только одну цену там, где маржинальный доход равен маржинальным затратам, это не гарантирует максимальной прибыли. Нужно выяснить, какой из двух максимумов прибыли является глобальным.

5.4.4. Ценовая оптимизация на олигопольном рынке

В случае олигополии компания должна учитывать реакцию конкурентов. Это значительно осложняет принятие ценовых решений. В целом при олигополии нет определенной оптимальной цены. Цена вместо этого зависит от предположительного поведения конкурентов. Проблема состоит в том, чтобы установить цену, которая окажется оптимальной после отклика конкурентов. Чтобы осуществить это эффективно, нужно брать в расчет функции реакции конкурентов, а не функцию «цена-отклик» потребителей:

Функция реакции r_i описывает, как олигополист i отреагирует на ценовые действия конкурента j. Теоретически можно обосновать различия индивидуальных функций реакции, поскольку конкуренты действительно могут реагировать по-разному. Однако определять подобные детализированные функции эмпирическим путем непрактично. Подобно прогнозированию функций «цена-отклик», имеет смысл использовать укрупненную форму функции реакции. Тогда средняя цена конкурентов будет служить пояснительной переменной с точки зрения олигополиста j. Получаем формулу

Отсюда необходимо определить только одну функцию реакции. Но это также значит, что любая дифференцированная реакция конкурентов не будет учтена. Компромиссным решением между функциями (5.4) и (5.5) будет сгруппировать бренды, демонстрирующие сходные реакции (например, магазинные бренды и заводские или брендированные товары и неизвестные марки). Как правило, обычно выбирают самую простую форму. Следуя данной логике, мы используем упрощенную версию.

Включаем функцию реакции (5.5) в функцию «цена-отклик» (без индекса продукта):

Получаем:

Объем продаж q здесь зависит от собственной цены p и конкурентной цены p, которая в свою очередь зависит от собственной цены. Чтобы определить оптимальную цену, мы дифференцируем функцию прибыли относительно p и устанавливаем производную, равную нулю:

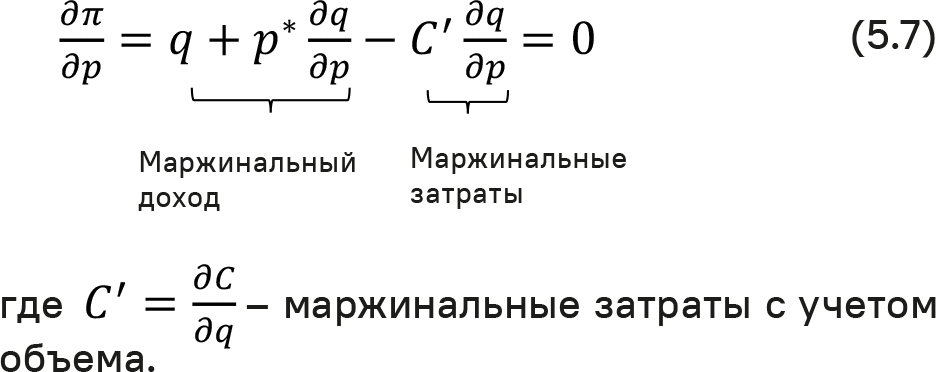
Фундаментальный принцип «маржинальный доход = маржинальные затраты» остается при олигиполии неизменным. Предприняв дополнительные шаги, мы получаем следующую формулу оптимальной цены²:

Эластичность реакции обозначает процентное изменение цены конкурентов, когда собственная цена меняется на 1 %.

В структурном смысле условие оптимальности напоминает формулу Аморозо – Робинсона (5.2). Однако на олигопольном рынке надбавка к маржинальным затратам определяется не только прямой ценовой эластичностью, но скорее «скорректированной» эластичностью, которая предусматривает конкурентную реакцию (e + sek). Выражение (e + sek) можно интерпретировать как «ценовую эластичность после конкурентной реакции».

Чтобы определить надбавку, нужно знать не только прямую ценовую эластичность, но и перекрестную эластичность и эластичность реакции.

Здесь мы снова отмечаем, что уравнение (5.8) не является решением для p*, поскольку все выражения в правой части уравнения могут зависеть от p*.

Перекрестная ценовая эластичность конкурирующих продуктов положительная. Эластичность реакции обычно бывает нулевой или положительной, то есть конкуренты либо вообще никак не отреагируют, либо сдвинут цены в том же направлении, что и инициатор изменения. В последнем случае оптимальная цена, с учетом реакции конкурентов, равна цене (или превышает ее), в которой реакция в расчет не принимается, а решения основаны на «монополистической» формуле Аморозо – Робинсона (5.2). Если эластичность реакции равна нулю, формула (5.8) удовлетворяет отношению Аморозо – Робинсона.

В случае мультипликативных функций «цена-отклик» и реакции формулу (5.8) можно использовать непосредственно как правило принятия ценовых решений. Давайте возьмем три значения: ценовая эластичность = –2, перекрестная эластичность = 0,5 и эластичность реакции = 1. Тогда уравнение дает коэффициент надбавки 3, если маржинальные затраты постоянные (то есть линейная функция затрат). Значит, надбавка к маржинальным затратам должна быть 200 %. Если перекрестная ценовая эластичность равна 0,6, процент надбавки возрастает на 250 %. Если эластичность реакции равна 0,5, при условии неизменности всех предыдущих параметров процентная надбавка будет всего 133 %. Пониженная эластичность реакции сокращает оптимальную надбавку.

Обзор

Обобщим ключевые аспекты ценовой оптимизации с учетом конкурентной реакции.

• Условия оптимальной цены при олигополии можно выразить формулой Аморозо – Робинсона.

• Оптимальная цена равна маржинальным затратам, помноженным на коэффициент надбавки, который зависит от прямой ценовой эластичности, перекрестной ценовой эластичности и эластичности реакции.

5.4.4.1. Линейная функция «цена-отклик», линейная функция реакции

Теперь рассмотрим случай линейных функций «цена-отклик» и реакции. В целом будем исходить из того, что функция затрат также линейная.

Если мы включим линейную функцию реакции

Чтобы получить оптимальную цену, можно применить правило монополистического принятия решений в формуле (5.3) к данной функции, скорректированной на реакцию:

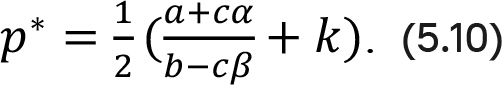
Отношение в круглых скобках соответствует максимальной цене, скорректированной на реакцию. Оптимальная цена лежит точно в срединной точке между этой максимальной ценой и переменными удельными затратами k. Оптимальная цена зависит от всех параметров в функциях «цена-отклик» и реакции.

Как и в случае с постоянными эластичностями, оптимальная цена в выражении (5.10) растет вместе с параметром конкурентной реакции b. Чем сильнее конкуренты реагируют на собственные ценовые изменения, тем выше будет оптимальная цена.

5.4.4.2. Реальный пример

Мы больше узнаем о поведении реакции, изучив реальный пример рынка бытовых чистящих средств. На рис. 5.8 показаны реальные ценовые тенденции для четырех ключевых брендов.

Рассматриваемый период времени – 2 года и 4 месяца. Как показывает визуальное наблюдение, цены на бренды A, B, C и D следовали одинаковому тренду. Отсюда следует, что имеет место взаимозависимость реакций. Линейная функция реакции (5.9) хорошо объясняет тенденции взвешенных по рыночной доле конкурирующих цен.

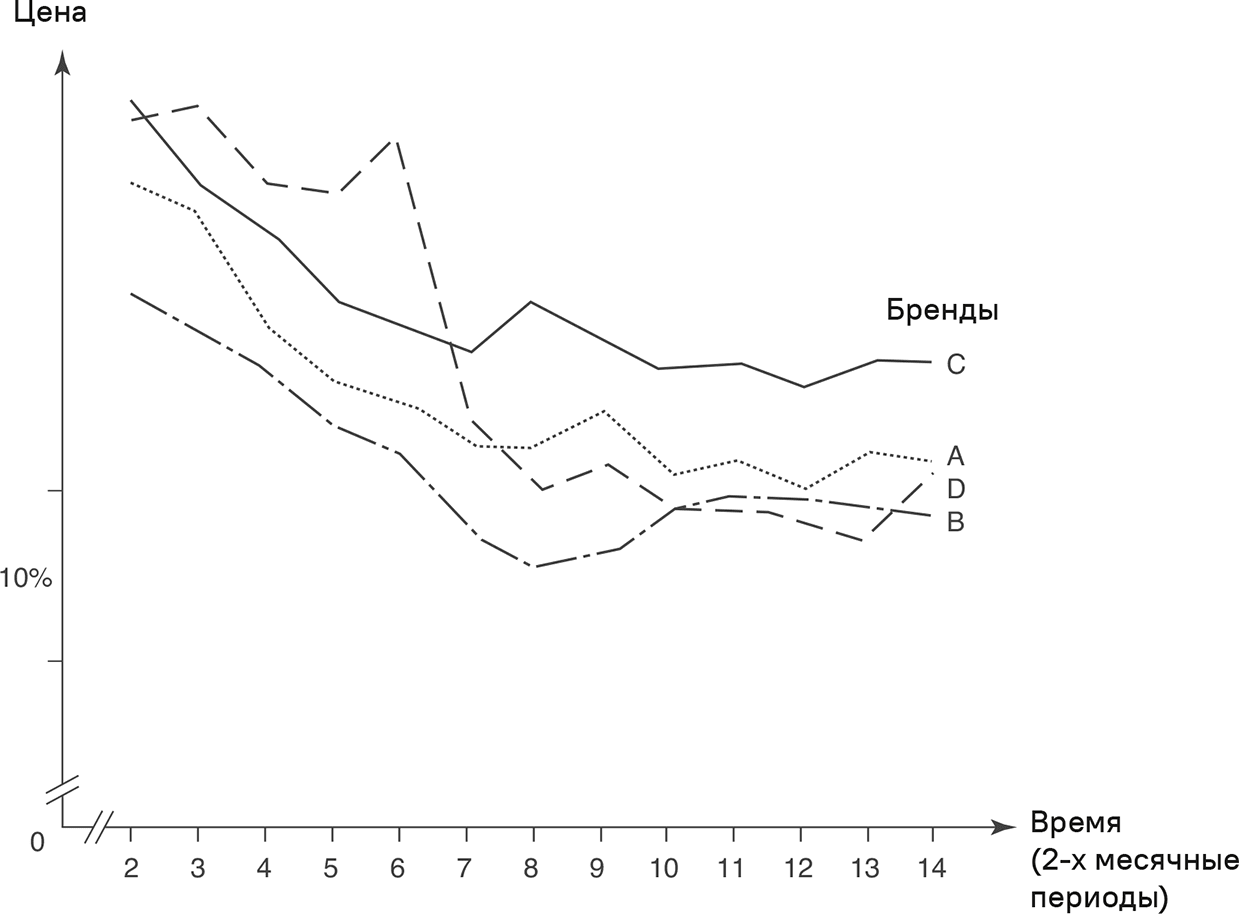
Рис. 5.8. Ценовые тенденции на рынке бытовых чистящих средств

Таблица 5.7. Линейная функция реакции для четырех бытовых чистящих средств

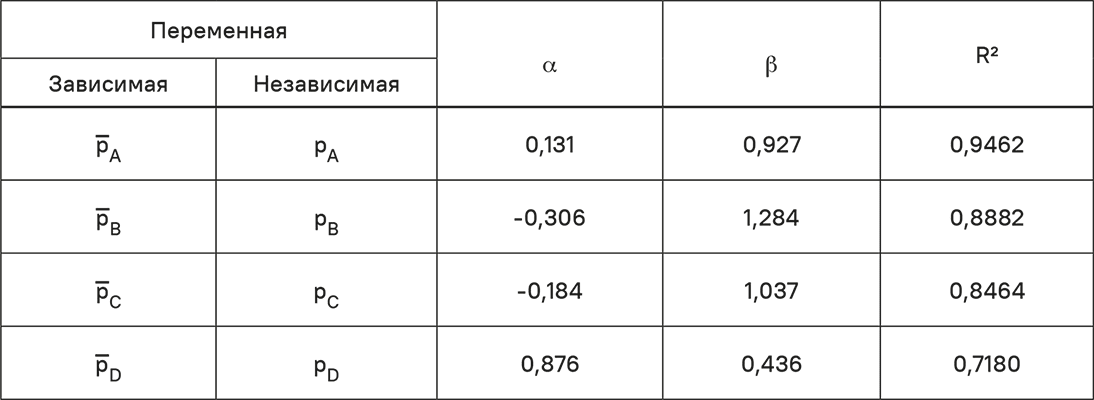
Коэффициенты детерминированности R2 везде высокие, все коэффициенты имеют статистическую значимость на уровне 10 %. Результаты показаны в табл. 5.7.

Чтобы продемонстрировать ценовую детерминированность, мы выбрали бренд D с коэффициентом реакции β = 0,436. Использованная здесь функция «цена-отклик» является вариантом, где разница цен (а не абсолютная цена) служит независимой переменной. Получаем функцию «цена-отклик» для D:

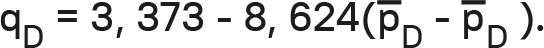
Скорректированная на реакцию максимальная цена для D равна $2,25 за килограмм, то есть скорректированная на реакцию функция «цена-отклик» пересекается с ценовой осью на $2,25. Маржинальные затраты составляют $0,85. Чтобы получить оптимальную цену с учетом конкурентной реакции, берем формулу (5.10) и получаем

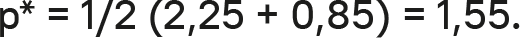
Если конкуренты реагируют согласно прогнозируемой функции, они тоже установят цены (в среднем) на уровне

0,876 + 0,436 x 1,55 = 1,55, то есть на том же уровне.

При данном ценовом варианте бренд D будет иметь объем продаж 3373 тонн и даст контрибуционную маржу $2,361 млн. Прямая и перекрестная ценовые эластичности равны в абсолютных значениях |ε| = ε_k = 3,96. Эластичность реакции σ равна 0,436: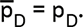

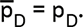
Интересно сравнить эту оптимальную цену со значением, выведенным без учета конкурентной реакции. Чтобы это продемонстрировать, возьмем конкурентную цену $1,55 и примем ее за данность. Оптимальная цена без конкурентной реакции выглядит так:

p* = 1/2 (1,94 + 0,85) = 1,40.

Если конкуренты никак не реагируют, на данном ценовом уровне бренд D получит объем продаж 4667 тонн с контрибуционной маржой $2,567 млн. Это на $2,361 млн больше, чем в вышеописанной ситуации. В действительности, то есть если измеренная функция реакции достоверна, конкуренты отреагируют и установят цены на уровне

p_D = 0,876 + 0,436 x 1,40 = $1,49.

По такой цене бренд D продаст всего 4149 тонн (вместо ошибочно спрогнозированных 4667 тонн). Контрибуционная маржа упадет на $2,282 млн, что меньше оптимального значения с учетом конкурентной реакции ($2,361 млн).

5.4.4.3. Ценовая оптимизация с субъективной оценкой конкурентной реакции

Субъективная оценка руководства может послужить альтернативой эконометрической корректировке функций реакции на основе ретроспективной ценовой информации. Исходя из таких оценок можно вывести функции «цена-отклик» с поправкой на реакцию. Данный подход показан на рис. 5.9.

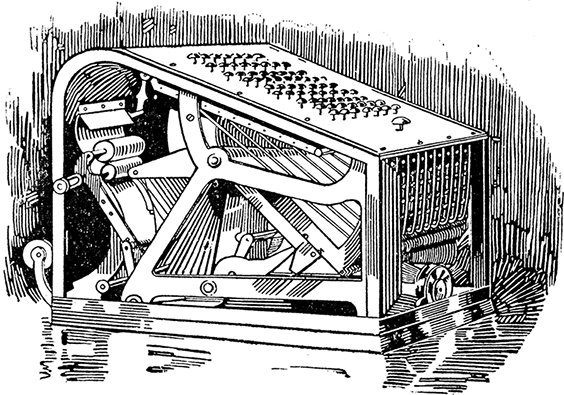
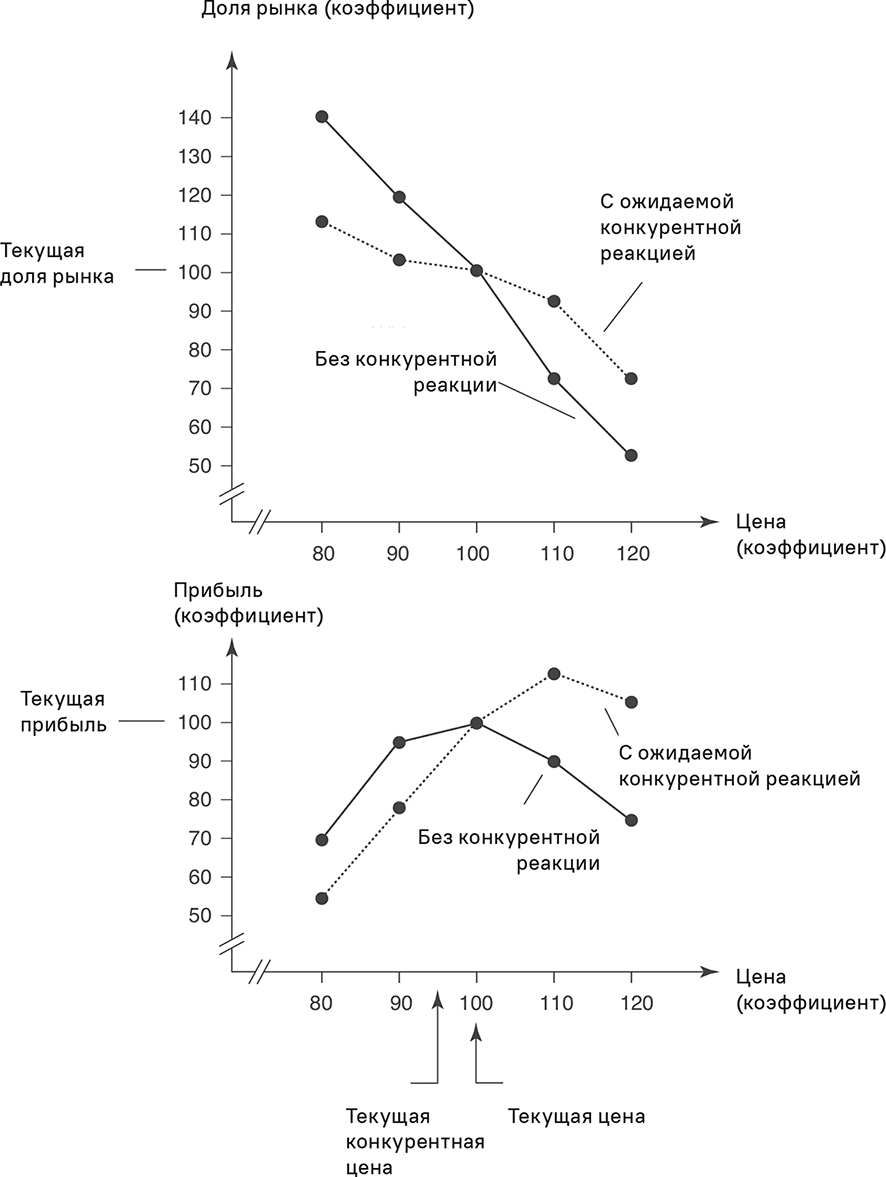
Рис. 5.9. Функции «цена-отклик» и кривые прибыльности на основе субъективной оценки

Руководителей просили предсказать ожидаемую реакцию конкурентов на пять альтернативных цен. Исходя из предполагаемой реакции были определены доли рынка. При снижении цены руководители ожидали от конкурентов реакции, как и при повышении цены на 10 %. И, напротив, руководители предполагали, что конкуренты не повторят повышения цены на 20 %. При такой реакции оптимально повысить цену на p = 110.

Метод субъективных оценок прост в применении и более гибок, чем вывод на основе рыночных данных функции реакции. Можно принимать в расчет все аспекты, влияющие на поведение реакции. С другой стороны, такие аппроксимации не всегда решают проблему конкурентной реакции. Руководители зачастую демонстрируют меньшую определенность в отношении конкурентных реакций, чем прогнозируемых функций «цена-отклик».

5.4.5. Допущения по поводу реакций на олигопольном рынке

Предположение о постоянной (то есть линейной или мультипликативной) функции реакции означает, что конкуренты будут реагировать на каждую ценовую подвижку так, как это обусловлено функцией. Теории олигопольного рынка, основанные на подобных жестких моделях реакций, называют эвристическими. Более сложные теории олигополии не предусматривают в обязательном порядке каких-то конкретных реакций, а вместо этого выводят реакции из контекста оптимизации. Главные побудительные мотивы, которые рассматривают данные теории, это понятия теории игр. Теория игр обеспечивает руководителям общие рамки стратегического мышления, даже если в ней мало строгих правил принятия ценовых решений.

Чтобы предвидеть реакцию конкурентов, нужно поставить себя в их ситуацию (так сказать, залезть им в голову) и задаться вопросом, какие реакции окажутся для них оптимальными. Очевидно, что основные условия, позволяющие ответить на такие вопросы, включают в себя знание целей, затрат, финансовой ситуации конкурентов и т. д., причем ответы на многие вопросы будут исходить из чисто спекулятивных рассуждений.

Ситуация осложняется еще больше, поскольку процесс мышления конкурентов включает в себя собственные домыслы относительно нашей реакции на их реакцию. На самом деле это может играть важную роль в принятии ими решений. Таким образом, нам необходимо предположить не только то, что конкурент думает относительно его собственной ситуации, но и что он думает о нашей. А теперь рассмотрим первый из этих трех этапов: как наши ценовые подвижки повлияют на конкурентов? Предположим, что конкурентов, как и нас, интересует максимизация прибыли. Таким образом, конкурент продемонстрирует реакцию только в том случае, если именно реакция, а не ее отсутствие, даст повышенную прибыль.

Чтобы легче понять причинно-следственные связи на олигопольном рынке и принимать соответствующие решения, мы будем использовать линейную функцию «цена-отклик». Рассматриваемая нами олигополия симметрична и состоит из олигополистов А и В (так называемая дуополия). Функция «цена-отклик» олигополиста i такова:

q_i = a – bp_i + cp_j; i, j = A, B

с параметрами a = 1000, b = 50, c = 25. Функция затрат также будет линейной с C_fix = $1000 и k = $5.

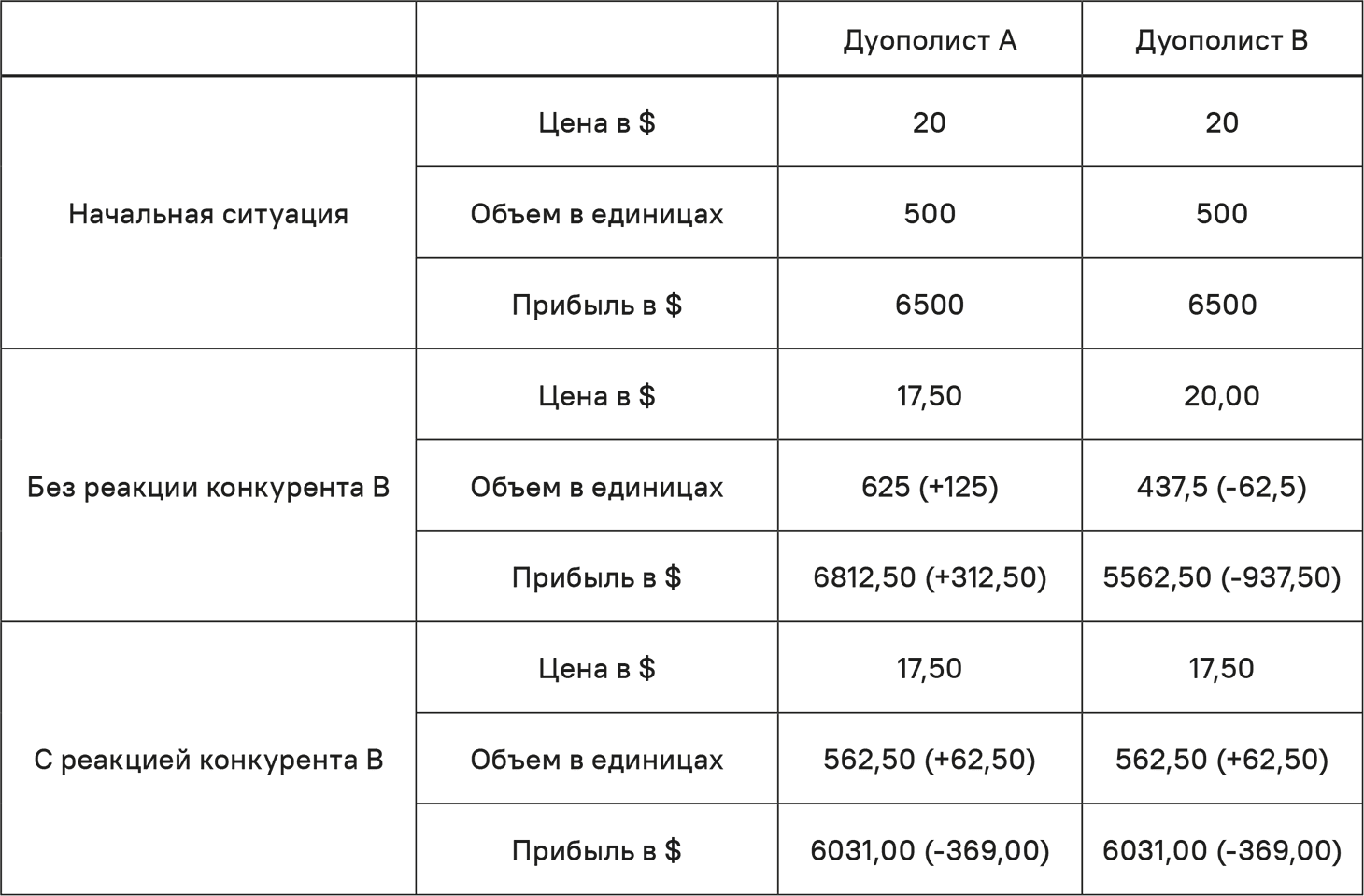
В табл. 5.8 представлены три ситуации. В начальной ситуации оба конкурента имеют одинаковую цену p_AO = p_BO = 20. Каждый продает 500 единиц и получает прибыль $500.

Теперь дуополист А анализирует свои цены. Мы рассмотрим два альтернативных случая.

В первом А считает, что В не отреагирует. Во втором А считает, что В отреагирует.

5.4.5.1. Гипотеза Курно

Вариант 1. А считает, что В не отреагирует и оставит текущую цену p_B0 = 20. Это соответствует так называемой гипотезе Курно – старейшей из эвристичеких моделей олигополии. Тогда функция «цена-отклик» А:

При данном предположении оптимальную цену можно рассчитать как для монополии по формуле (5.3). Получаем:

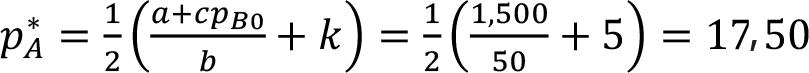
Эта цена называется «цена Курно». Если В на самом деле не реагирует, А получает объем продаж 625 единиц и прибыль $6812,50, которая выше, чем прибыль $6500 в начальной ситуации. Что происходит с прибылью В? Если В не делает ничего, его клиенты уходят к А. Объем В снижается с 500 до 437,50 единиц, а прибыль падает до $5562,50. Результаты показаны в табл. 5.8.

Предположим, что дуополист В не такой тупой и неинформированный и не пожелает согласиться с уменьшением прибыли. Скорее всего, В отреагирует. Если В также снизит цену на $17,50, функция «цена-отклик» А будет:

Из-за реакции В объем продаж А не увеличится до 625 единиц, как изначально (и некорректно) предположил А. Объем увеличится только до 562,50 единиц, а прибыль будет всего $6031. Это меньше, чем начальная прибыль $6500. Прибыль В также упадет до $6031, но всё же это лучше, чем прибыль при «ничегонеделании» – всего $5562. Результаты показаны в табл. 5.8. Так что велика вероятность, что В отреагирует на снижение цены А собственным снижением цен. Если А этого ожидает, он воздержится от снижения цены и оставит ее на прежнем уровне $20, поскольку снижение цены вместе с реакцией В ухудшит ситуацию А.

Таблица 5.8. Результаты при реакции и без нее

5.4.5.2. Гипотеза Чемберлина

Вариант 2. Проанализировав свою ценовую политику, А считает, что В в полном объеме отреагирует на изменение цены, то есть здесь применима функция «цена-отклик» в выражении (5.11). Если А проведет оптимизацию исходя из данной предпосылки, оптимальная цена будет:

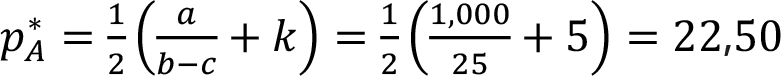
Это так называемая цена Чемберлина. При этой цене A продаст 437,50 единиц и получит прибыль $6656, что выше первоначальной прибыли $6500.

Каковы последствия для В? Если В отреагирует так, как предполагает А, и поднимет цену до $22,50, В также получит прибыль $6656, что лучше начальной ситуации. Но В сделает еще лучше, если не отреагирует. В этом случае его объем продаж вырастет до 562,50 единицы за счет притока клиентов от А. Прибыль В повысится до $7438. Если предположить, что на этом размышления В окончатся, он не отреагирует на повышение цены А. Однако «ничегонеделание» В означает, что цена А, повысившаяся до $22,50, снизит прибыль А до $5562,50. Если А, таким образом, думает, что В не отреагирует, то он быстро откажется от решения поднять цену и оставит ее на прежнем уровне.

5.4.5.3. Интерпретация теории игр

Вышеописанный процесс мышления представляет собой разумное поведение дуополиста В, а не приверженность жестким реакциям. Но процесс размышлений В (или, по крайней мере, представление о нем А) завершился как минимум на один шаг раньше, чем необходимо.

Процесс мышления был такой:

• В не реагирует на повышение цены А, потому что реакция «ничегонеделания» для В лучше.

• А знает это и решает не поднимать цену. Обе компании остаются при начальной ситуации.

Таблица 5.9. Олигополия как «дилемма заключенного»

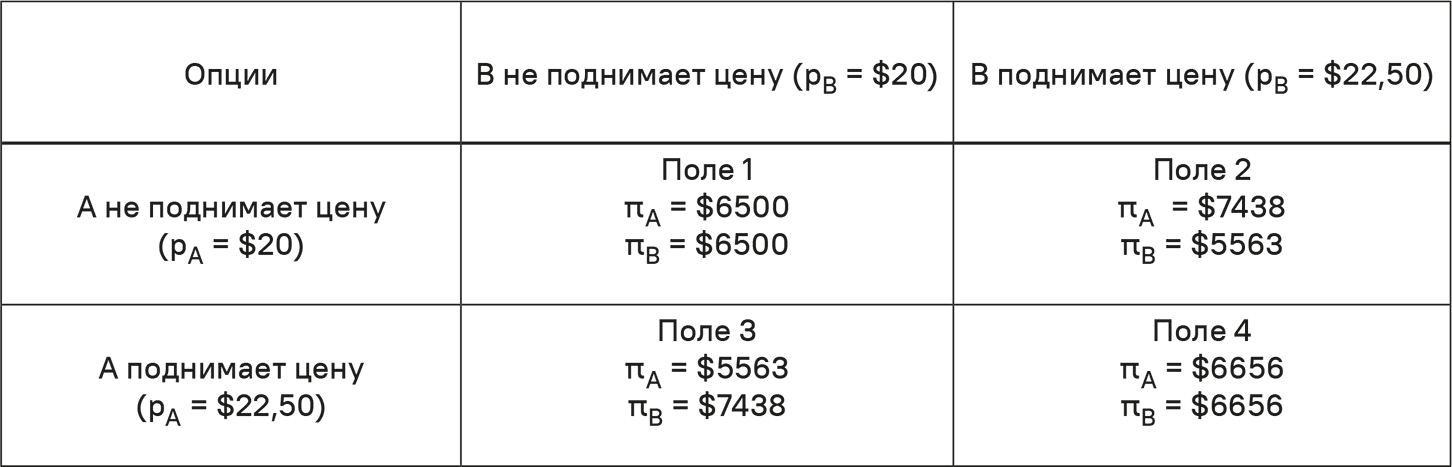
Если В продолжит размышления, то поймет, что его реакция «ничегонеделания» на повышение цены А для него выгоднее, однако она помешала А эту цену повысить. Такой тупик осложняет положение обеих сторон и оставляет прибыль В на уровне GB = 6500, что ниже его прибыли GB = 6656, если бы он повысил цену, как и А.

Ситуация, представленная в табл. 5.9, известна в теории игр как «дилемма заключенного». Вариант «не поднимать цены» соответствует «предательству» другого заключенного. Вариант «поднимать цены» – эквивалент опции «хранить молчание».

Успех олигополиста зависит от его реакции на действия конкурентов. Ценовые изменения конкурентов могут оказать немедленный и заметный эффект на собственную прибыль. Ценовые изменения в олигополии осложняются большей неопределенностью из-за возможных реакций конкурентов. Самый простой способ снизить неопределенность – это договориться с другими олигополистами. Но такие ценовые картели не только запрещены антимонопольными законами и законами в защиту конкуренции, но и наказание за них бывает очень суровое.

Ценовая ситуация приобретает характер дилеммы, в частности, если повышение цен является обязывающим на длительный период времени (по организационным, договорным или иным причинам).

Если А повышает цену, а В нет, то прибыль А ухудшается (Поле 3, p_A = $22,50; p_B = $20). Этот вариант привлекателен для В, поскольку в Поле 3 у него хорошая позиция. Повышение цены здесь связано с риском для компании, которая проявляет инициативу, – говорят, что она берет на себя «роль мученика». Мученик рискует еще и тем, что ему придется тоже повышать цену, что подорвет его имидж. Если А не доверяет В, то А выбирает стратегию, которая в худшем случае принесет ему максимальную прибыль (стратегия «максимум-минимум»). Иными словами, он оставит цену неизменной на p_A = $20. Прибыль А в $6500 на этом уровне подвергается риску меньше всего.

Но если А, исходя из прежнего опыта, может предположить, что В повысит цену вслед за ним, тогда А поднимет цену. Если В действительно тоже повысит цену, согласно гипотезе Чемберлина, прибыли обоих дуополистов вырастут по сравнению с прибылью в начальной ситуации и будут представлять собой коллективный максимум. Этой ситуации также можно добиться с помощью расчетов «издержки плюс» с отраслевыми надбавками, следуя стратегии ценовых корректировок или за счет ценового лидерства. Такие универсальные правила дают при олигополии оптимальные результаты. Stigler [16] считает лучшим решением проблемы олигополии ценовое лидерство. В пользу данной стратегии говорит очень многое. Она приносит удовлетворительные результаты всем конкурентам, по крайней мере, если у них сходные позиции по затратам и объемам продаж. Но она не свободна от ограничений. Ценовое лидерство и сходные модели поведения требуют хорошего стратегического мышления и взаимного доверия между конкурентами. Также необходимо определенное сходство по затратам, целям и структуре спроса. Такие условия с наибольшей вероятностью возникают на устоявшихся, зрелых рынках со стабильным числом конкурентов, которые «хорошо знают друг друга». Но даже при подобных обстоятельствах по-прежнему существуют «неразумные» отрасли или компании, которые ведут ценовые войны.

На динамичных рынках слаженное поведение – редкий случай. Новые конкуренты, особенно из других стран или отраслей (диверсификация), обычно не склонны следовать устоявшимся правилам ценообразования и силой прокладывают себе путь на рынок с помощью агрессивных цен. Там, где существуют или возможны различные позиции по затратам (например, за счет эффектов кривой эффективности или сетевых эффектов), ценовое равновесие также вряд ли возможно. Новый растущий рынок внутригородских и междугородных автобусных маршрутов в Европе и возрожденные рынки в некоторых регионах США с самого начала испытали ценовые войны. Они были такими жестокими, что некоторые конкуренты не продержались больше года [17]. На ранних этапах развития рынка мышление конкурентов сосредоточено на двух целях. Во-первых, они хотят с помощью низких цен пересадить клиентов с поезда на автобус. Во-вторых, они стремятся финансово выдавить с рынка слабых конкурентов и получить их долю рынка [18]. За три года Flixbus достигла обеих целей. Сейчас она занимает больше 90 % рынка Германии, и у нее осталось только три конкурента [19]. После подобных слияний и поглощений цены, как правило, начинают идти вверх. На данном рынке так и случилось, цены выросли в среднем на 15 % в течение одного квартала [20].

Рынок облачных сервисов оказался в аналогичной ситуации, когда начались ценовые войны между Amazon и Google [21]. Финансовая мощь конкурентов имеет решающее значение для успеха или неудачи, особенно на ранних этапах становления рынка. Более сильные компании дольше способны нести убытки или упускать прибыль, когда расширяют свои возможности и рыночные доли.

Обзор

Обобщим ключевые моменты оптимизации цен при олигополии.

• При олигополии нет определенной оптимальной цены. Оптимальная цена зависит от реакции конкурентов. Таким образом, эти реакции необходимо учитывать при ценообразовании.

• Олигополии могут успешно установить или, по крайней мере, приблизиться к установлению коллективной монопольной цены, если выполняются следующие условия: у конкурентов сходные позиции по затратам и долям рынка, похожие цели, достаточный уровень стратегической мудрости и определенное доверие друг к другу.

• Для олигополий лучше воздерживаться от значительных ценовых изменений, если данные условия не применимы либо если один или более олигополистов решат по какой-либо причине не приближать свои цены к коллективной монопольной цене. Можно, однако, повысить цены, чтобы компенсировать повышенные затраты, которые влияют на всех олигополистов. Аналогичным образом снижение цен может не дать устойчивого преимущества его инициатору, поскольку конкуренты, скорее всего, ответят тем же и развяжут ценовую войну.

5.4.5.4. Сигнальная стратегия

Сигнальная стратегия – это публичные индикаторы, или сигналы, которые олигополист посылает рынку при подготовке планируемых ценовых корректировок. Такие сигналы могут транслироваться через прессу, радио, телевидение, Интернет и другие каналы коммуникации. Porter [22] определяет рыночный сигнал как «любое действие конкурента, являющееся прямым или косвенным индикатором его намерений, мотивов, целей или внутренней ситуации». Сигналы могут подаваться в форме действий или заявлений [23]. Считается, что заявления вызывают меньше доверия, чем действия, поскольку некоторые компании блефуют в надежде дезориентировать конкурентов. Для эффективной сигнальной стратегии действия компании должны соответствовать заявлениям, и наоборот [24].

Концепция сигнальной стратегии исходит из того, что действия компании вызовут некую реакцию, если компания испытывает конкуренцию, то есть перекрестная эластичность цен не равна нулю [25]. Данная концепция поднимает вопрос о целях, которые ставят перед собой конкуренты, осуществляя снижение или повышение цен. Интерпретация этих целей может стать сигналом, за которым точно так же последует реакция.

Сигнальная стратегия может помочь компании:

• помешать или разубедить потенциального конкурента выходить на рынок;

• обосновать ценовые изменения, особенно снижение цен. Например, если продукт компании находится в конце жизненного цикла, компания может сделать на него скидку, чтобы распродать товарные запасы. Сигнал об этом намерении и ограниченный период времени могут помешать конкурентам истолковать это снижение цены как агрессивное и тоже снизить цены;

• вызвать у конкурентов определенное поведение. Это может оказаться важным при повышении цен. В этих случаях компании часто подают сигнал о рациональном обосновании такого повышения, так что не только конкуренты, но и клиенты (ритейлеры, торговые посредники, потребители) это понимают и идеально воспринимают необходимость роста цены.

Интерпретировать рыночные сигналы крайне необходимо. Снижение цены одним из конкурентов может представлять собой попытку получить долю рынка или распродать товарные запасы [26]. Первое может восприниматься как более агрессивное действие [27]. Эта ситуация объясняет, почему одна и та же ценовая подвижка может вызывать разные отклики.

Точный анализ характеристики сигналов дает ценную информацию о намерениях конкурента. Heil and Bungert [28] дают следующую классификацию характеристик сигналов.

• Эффект сигнала описывает оценку реагирующей компании той степени, в которой объявленные или внедренные конкурентом изменения цен влияют на собственную прибыль или долю рынка компании.

• Агрессивность сигнала определяется величиной изменения цены и соответствующей угрозой, которую она представляет для конкурентов.

• Сигнал считается четким, если он оставляет небольшую возможность для его интерпретации. Четкие сигналы зачастую приводят к немедленным откликам. Нечеткие сигналы оставляют больше места для (неверного) истолкования.

• Непротиворечивость сигнала – это единообразие сигналов, которые компания посылает на другие рынки или в рыночные сегменты.

• Степень, в которой сигнал является обязывающим, это функция его обратимости.

• Надежность компании, посылающей сигнал, влияет на вероятность реализации заявленного плана на практике. Это решающий фактор сигнальной стратегии.

Рынок автострахования в Германии предлагает пример успешной сигнальной стратегии. На рынке годами шли ценовые войны, подогреваемые одним из рыночных лидеров.

В октябре 2011 года в немецкой деловой прессе прошло сообщение, что «крупнейшая страховая группа Германии Allianz собирается резко поднять цены с 1 января 2012 года» [29]. Все другие страховые компании публично заявили, что тоже поднимут цены. В течение 2012 года цены в среднем выросли на 7 %. Потом председатель совета директоров HUK-Coburg, крупнейшего соперника Allianz, объявил, что «в 2013 году цены снова поднимутся» [30]. И цены действительно выросли в 2013 году примерно на 6 %. Ценовое лидерство имеет место лишь в том случае, если компания принимает на себя эту роль, а конкуренты признают ее лидером.

Также компании подают сигналы об ответных мерах в попытке разубедить конкурентов прибегать к таким шагам, как снижение цен. Им Так-Ук, исполнительный директор корейского автопроизводителя Hyundai, публично заявил, что если «японские автопроизводители будут осуществлять агрессивные акции, и мы не сможем выйти на целевой уровень продаж, то мы тоже рассмотрим вариант о льготах для покупателей» [31]. «Льготы» – это повышенные скидки или, другими словми, снижение цен. Заявление – четче некуда.

Такие заявления, однако, надо формулировать очень внимательно, во избежание риска нарушить антимонопольное законодательство или закон о конкуренции. Любые прямые призывы конкурентов к координированию действия не только запрещены, но и любое «послание в бутылке» или письмо клиентам с целью проинформировать их о повышении цен может расцениваться критически, если будет воспринято как намерение проинформировать конкурентов, а не потребителей. Компания должна следовать четким правилам в отношении корпоративных коммуникаций, чтобы не привлекать внимания антимонопольных органов.

Обзор

Обобщим ключевые аспекты сигнальной стратегии.

• Ценовые изменения на олигопольном рынке должны тщательно готовиться. Сигнальная стратегия – это средство заблаговременно донести свое намерение до рынка и, как результат, вызвать желаемый отклик других олигополистов.

• Сигнальная стратегия информирует всех участников рынка о запланированном действии.

Конкуренты получают возможность самим послать сигнал и/или скорректировать свое поведение. Также сигналы информируют клиентов. Это повышает степень приемлемости повышения цен или усиливает эффекты снижения цен.

• Сигнальная стратегия может повысить шанс благоприятного результата для всех олигополистов.

Назад: 5.3. Жесткие процессы ценообразования

Дальше: Заключение