Сегодня мы называем ДУЧП д’Аламбера волновым уравнением и интерпретируем его решение как суперпозицию симметрично расположенных волн, из которых одна движется со скоростью а, а вторая со скоростью – а (они перемещаются в противоположных направлениях). Это стало одним из самых важных уравнений в математической физике, потому что в природе волны встречаются повсюду, причем самые разные.

Эйлер ознакомился с работой д’Аламбера и тут же постарался улучшить ее. В 1753 г. он показал, что без граничных условий общее решение будет выглядеть так:

где f и g периодичны, но не удовлетворяют никаким другим условиям. В частности, эти функции могут иметь различные формулы для разных областей x – особенность, которую Эйлер считал свойством функций, имеющих разрывы, хотя в современной терминологии они непрерывны, но имеют разрывную первую производную.

В более ранних работах, опубликованных в 1749 г., он указывал, что (для простоты мы принимаем, что длина струны равна единице) простейшие нечетные периодические функции являются тригонометрическими:

и т. д. Эти функции представляют простые синусоидальные колебания с частотой 1, 2, 3, 4 и т. д. Эйлер утверждал, что общим решением здесь является наложение (суперпозиция) таких кривых. Базовая синусоида sin x является основной модой колебаний, а остальные будут более высокими модами, – в итоге получается то, что мы теперь называем гармониками.

Сравнение решений волнового уравнения, предложенных Эйлером и д’Аламбером, привело к фундаментальному кризису.

Д’Аламбер не признал возможности существования разрывных функций в интерпретации Эйлера. Более того, рассуждения Эйлера грешили одной нестыковкой, поскольку тригонометрические функции всегда непрерывны, и, следовательно, конечны наложения (суперпозиции) из них. Эйлер предпочел не углубляться в это противоречие между конечными и бесконечными суперпозициями. Впрочем, в те дни никто не был очень строгим в подобного рода вопросах и никто из ученых еще не ступил на этот сложный путь важности обоснования новых методов. Однако в итоге такое упущение привело к серьезным проблемам. На время разногласия утихли, пока новая работа Фурье не подлила масла в огонь.

Последовательность изображений волны, движущейся слева направо

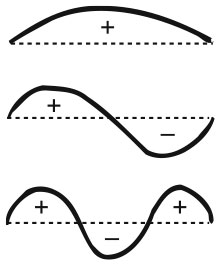
Режимы колебаний струны