Алгоритмы

Книга: Укрощение бесконечности. История математики от первых чисел до теории хаоса

Математика внесла свой вклад в компьютерную науку, но и компьютерная наука подтолкнула к открытию поразительной новой математики. По одному из определений, алгоритм – систематический порядок действий для решения задачи. Это слово восходит к арабскому ученому Аль-Хорезми. И тут возникает любопытный вопрос: как зависит время работы алгоритма от объема вводимых данных?

Например, алгоритм Евклида для нахождения наибольшего общего делителя двух целых чисел m и n, где m ≤ n, выглядит так.

• Разделить n на m и получить остаток r.

• Если r = 0, то наибольший общий делитель – m: СТОП.

• Если r > 0, тогда заменить n на m, а m на r и вернуться к началу.

Можно показать, что если m включает d десятичных цифр (мера объема вводимых данных для алгоритма), то алгоритм останавливается максимум после 5d шагов. Это значит, в частности, что если нам заданы два числа с 1000 цифр, то мы можем вычислить их наибольший общий делитель не более чем за 5000 шагов – на что современному компьютеру требуется доля секунды.

Алгоритм Евклида имеет линейное время работы – продолжительность вычислений, пропорциональную объему (в цифрах) вводимых данных. В более широком смысле алгоритм имеет полиномиальное время работы, или относится к классу P, если его время работы пропорционально некой фиксированной степени (квадрат или куб) от объема вводимых данных. В противоположность этому все известные алгоритмы для нахождения простых множителей числа имеют экспоненциальное время работы – некую фиксированную константу в степени, зависящей от объема вводимых данных. Это и делает (гипотетически) безопасной криптосистему RSA.

Проще говоря, алгоритмы с полиномиальным временем работы применяются на практике в вычислениях на современных компьютерах, а алгоритмы с экспоненциальным временем работы – нет, и соответствующие подсчеты для них на практике произвести невозможно, даже для относительно малых объемов вводимых данных. Это отличие является эмпирическим правилом: полиномиальный алгоритм может иметь такую большую степень, что будет непрактичным, и некоторые алгоритмы со временем работы, худшим, чем полиномиальное, всё равно на поверку оказываются полезными.

Тут возникает главная теоретическая трудность. Если взять определенный алгоритм, для него можно довольно легко подсчитать, как его время работы зависит от объема вводимых данных, и определить, относится он к классу P или нет. Но невероятно трудно решить, существует ли более эффективный алгоритм, который быстрее решит ту же задачу. Итак, хотя мы знаем, что многие задачи способен решить алгоритм класса P, мы понятия не имеем о том, не относится ли любая серьезная задача к классу не-P.

Здесь полезно вспомнить о технической интерпретации. Некая проблема должна быть не-P просто потому, что для получения ответа требуется не-P время работы. Например, нам надо составить список всех возможных способов расставить по порядку n символов. Чтобы работать с такой явно не-P проблемой, нужна другая концепция: класс NP недетерминированных полиномиальных алгоритмов. Алгоритм относится к классу NP, если любой предполагаемый ответ можно проверить за время, пропорциональное некоторой фиксированной степени, зависящей от объема вводимых данных. Например, угадав простой множитель большого числа, мы легко можем проверить его одним делением.

Задача из класса P автоматически является задачей из класса NP. Многие важные задачи, для которых неизвестны P-алгоритмы, имеют такие алгоритмы в NP. Мы подошли к самой серьезной и сложной проблеме в данной области, за решение которой объявлена премия в миллион долларов Математическим институтом Клея. Являются ли классы P и не-P одним и тем же? Самым правдоподобным ответом кажется «нет», поскольку P = NP означает, что многие из считавшихся чрезвычайно сложными вычислений на самом деле легки – просто мы пока не нашли упрощающих их преобразований.

ЧТО ЧИСЛЕННЫЕ МЕТОДЫ ДАЮТ НАМ
Численные методы играют центральную роль в проектировании современных воздушных судов. Совсем недавно инженерам приходилось конструировать аэродинамические трубы, чтобы проверить, как поток воздуха будет обтекать проектируемые ими крылья и фюзеляжи. Они помещали в такую трубу модель своего самолета, с помощью вентилятора нагнетали поток воздуха и следили, что происходит. Уравнения Навье – Стокса позволяли делать разные теоретические догадки, но не могли применяться к реальным воздушным судам, имевшим слишком сложные формы.

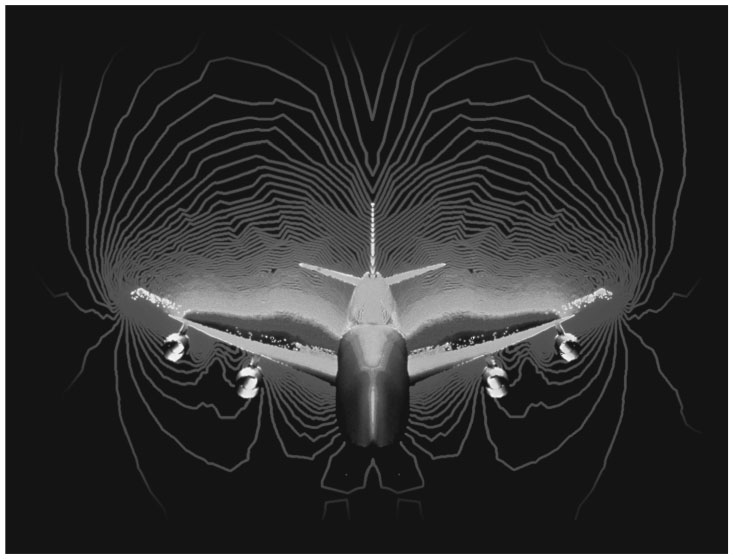
Численный расчет обтекания воздухом движущегося самолета

Сегодняшние компьютеры настолько мощны, а численные методы для решения ДУЧП стали такими эффективными, что во многих случаях реальная аэродинамическая труба уступает место цифровой – компьютерной модели самолета. Уравнения Навье – Стокса так точны, что их можно без опаски использовать при таком подходе. Преимущество компьютерного моделирования в том, что любая мыслимая особенность воздушного потока может быть визуализирована и проанализирована.

Проблему «P = NP?» усугубляет загадочный феномен, получивший название NP-полной задачи. Многие задачи NP таковы, что если они действительно сводятся к классу P, то и любая другая задача из NP сводится к классу P. Такая задача и называется NP-полной. Если для конкретной NP-полной задачи может быть доказано, что она является P, то P = NP. А если для некоторой NP-полной задачи может быть доказано, что она не-P, то P – не то же, что NP. Одной из NP-полных задач, недавно привлекшей внимание ученых, была задача, связанная с популярной компьютерной игрой «Сапер». В математической интерпретации она известна как задача выполнимости булевых формул: есть некое высказывание математической логики; будет ли оно истинным, если присвоить значения «истина» или «ложь» ее переменным?

Назад: Компьютерам нужна математика

Дальше: Численные методы