ГЛАВА 9
СОЗДАНИЕ РАБОЧЕГО РАСПИСАНИЯ ПРОЕКТА
После того как вы подготовили соответствующую сетевую диаграмму расписания проекта, в которой определена продолжительность всех работ, нужно определить, где в ней расположен самый длинный путь (отрезок), и понять, соответствует ли он дате завершения проекта. Поскольку этот самый длинный отрезок определяет минимальную продолжительность проекта, любые работы на нем вызовут смещение даты окончания всего предприятия. Поэтому этот путь называется критическим путем.
РАСЧЕТ РАСПИСАНИЯ ПРОЕКТА
Обычно расчет расписания проекта делает компьютер. Однако я уверен, что, пока вы не поймете, как осуществляются эти расчеты, вы не поймете и значение резервов времени, назначения более ранних и более поздних дат и т. д. Более того, вы рискуете стать жертвой механизма «мусор на входе — мусор на выходе». Поэтому я вкратце расскажу, как расчет расписания делается компьютером. (В большинстве программ компьютер сам переводит время в календарные даты, что не так легко сделать вручную.)
Первое: подумайте о том, что нам нужно знать о проекте. Если он начинается в некое время = 0, мы хотим знать, когда он может быть завершен. В живых и актуальных проектах нам всегда называют дату, к которой он должен быть закончен. То есть дату окончания проекта нам диктуют. Кроме того, начало проекта всегда имеет обременения: не готовы ресурсы, не написаны спецификации или к этому моменту еще не завершился другой проект. Так что составление расписания проекта обычно представляет собой попытку вместить работу между двумя точками во времени. Несмотря на это, мы все же хотим знать, сколько нужно времени до исполнения проекта. Если это время не вписывается в требуемые временные рамки, придется что-то делать с сокращением критического пути.
В самом простом варианте расчет сетевой диаграммы расписания проекта делается исходя из предположения, что продолжительность всех работ по проекту точно соответствует заданию. Однако их продолжительность зависит от уровня обеспеченности работ ресурсами, а если к моменту начала ресурсов в действительности будет не хватать, нереальны и даты решения задач, указанные в расписании.
Именно по этой причине расчет сетевой диаграммы расписания проекта должен осуществляться с учетом возможной ограниченности ресурсов. Другими словами, распределение ресурсов необходимо для того, чтобы понять, какое именно расписание проекта выполнимо! Неудачное определение ресурсов по проекту почти всегда приводит к невыполнимости расписания.
Таким образом, первым делом в расчете сетевой диаграммы расписания нужно определить критический путь и возможный объем некритических работ при идеальных условиях. Разумеется, идеальны условия, при которых проект обеспечен неограниченными ресурсами, поэтому первые расчеты сети расписания совершаются без учета возможных требований с точки зрения ресурсов. Этот метод описан в данной главе, а вопросы распределения ресурсов рассматриваются в руководствах по программному обеспечению подготовки расписаний.
ПРАВИЛА СЕТИ РАСПИСАНИЯ ПРОЕКТА
Для расчета времени начала и окончания сети расписания проекта применяются только два правила: правило 1 и правило 2. Другие правила компьютерные программы могут применять сами. Обычно, это функция конкретной программы, поэтому не имеет отношения ко всем сетям.
ПРАВИЛО 1. Прежде чем начнется выполнение конкретной задачи или работы, все предшествующие работы должны быть завершены.
ПРАВИЛО 2. Стрелки обозначают логический порядок работ.
БАЗОВЫЕ РАСЧЕТЫ РАСПИСАНИЯ
Расчеты расписания проиллюстрированы в диаграмме сети (рис. 9.1). Сначала внимательно посмотрим на квадратики в диаграмме. В каждом из них содержатся сокращения РС, ПС, РФ, ПФ и ПР.
РС — ранний старт;
ПС — поздний старт;
РФ — ранний финиш;
ПФ — поздний финиш;
ПР — продолжительность (выполнения работы или решения задачи).
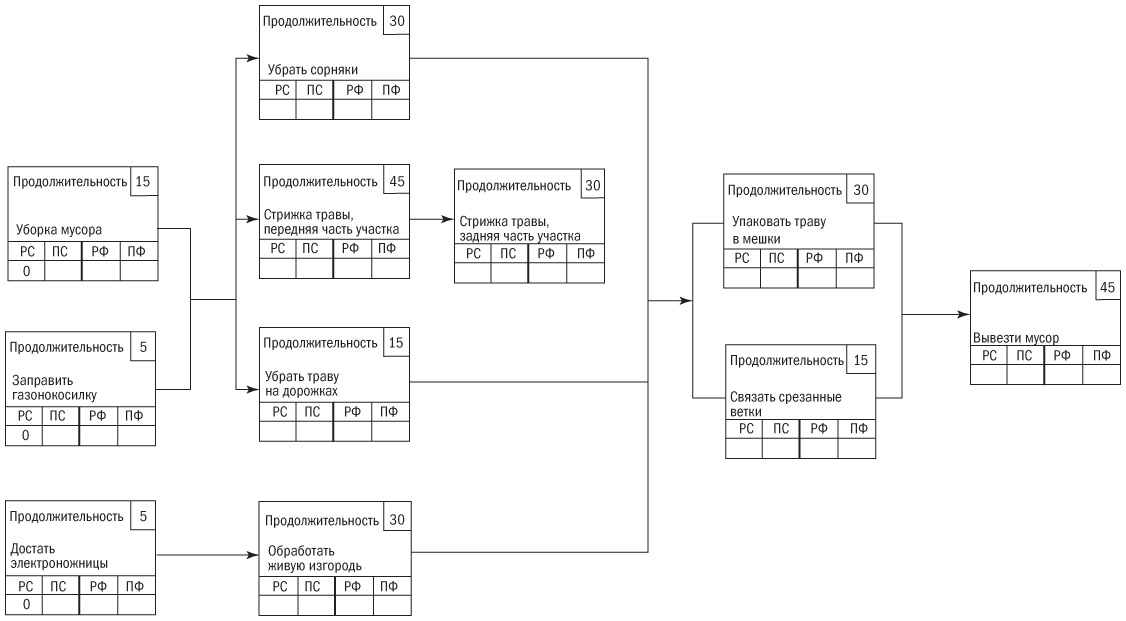
Рис. 9.1. Сеть расписания, которая иллюстрирует принципы его расчета
Вычисления с направленностью вперед
Посмотрите на какую-нибудь отдельную работу, внесенную в сеть расписания, например уборку мусора на участке. Ее продолжительность 15 минут. Если предположить, что она начнется с временной точки 0, то может быть закончена через 15 минут. Значит, мы можем внести число 15 в ячейку, помеченную как РС.
Заправка бензином газонокосилки и культиватора для устранения сорняков занимает всего пять минут. Логика диаграммы говорит нам, что обе эти задачи должны быть выполнены до того, как мы начнем выпалывать сорняки, косить траву и убирать ее с дорожек. Уборка мусора занимает 15 минут, а заправка косилки и культиватора — только пять. Когда могут быть начаты следующие работы? Только тогда, когда закончится уборка мусора, потому что это самая продолжительная задача из первых работ.
Ранний финиш уборки мусора становится ранним стартом других работ. Всегда действует порядок: ранний финиш начальных работ становится ранним стартом работ последующих. То есть самый длинный отрезок первых работ определяет, как рано могут начаться следующие работы.
Следуя этому правилу, мы можем внести время раннего старта для каждой задачи (рис. 9.2). В результате узнаем, что для завершения всего проекта нам нужно 165 минут, если работы будут выполняться в соответствии с диаграммой сети расписания. Мы только что осуществили вычисления с направленностью вперед, чтобы определить по всем задачам их самые ранние стартовые точки. Компьютерные программы делают то же самое и в дополнение к этому переводят время в календарные дни.
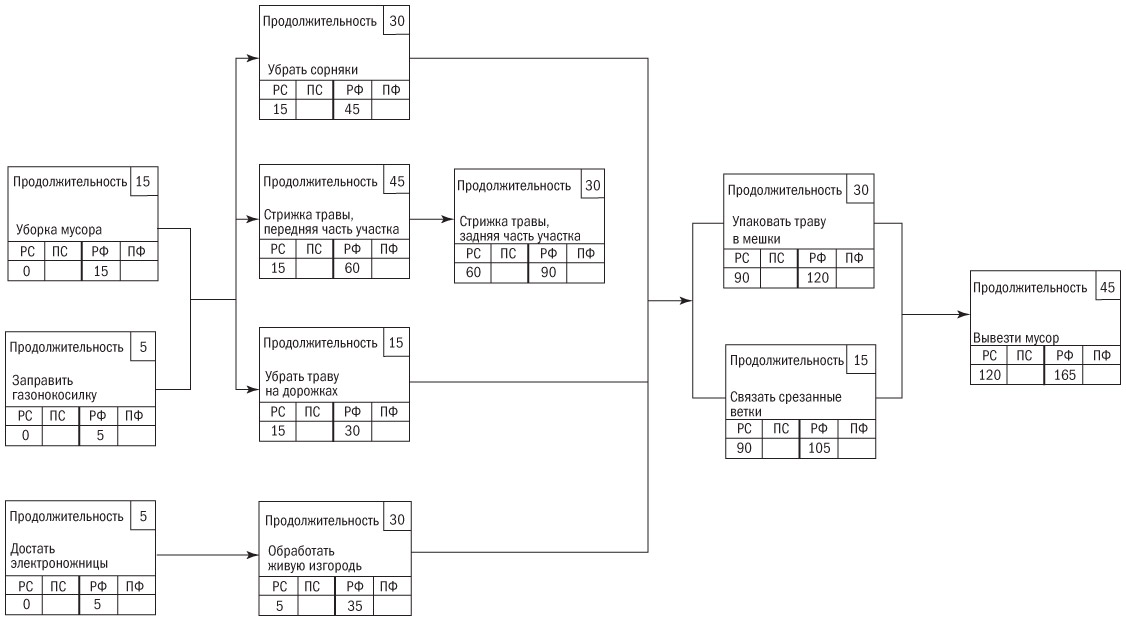
Рис. 9.2. Сетевая диаграмма расписания с указанием ранних финишей
ПРАВИЛО. Когда две или более работ или задач предшествуют другой задаче, самое раннее время ее начала определяется наибольшей продолжительностью предшествующей работы.
ПРИМЕЧАНИЕ. Время, определенное для завершения проекта или наступления его последнего события, является временем самого раннего его финиша в рамках существующих норм рабочего времени. Если принять во внимание выходные, праздники и другие перерывы в расписании, дата окончания проекта может оказаться значительно более поздней, чем финиш проекта, предусмотренный только рабочим временем.
Вычисления с обратной направленностью
Расчет расписания по принципу обратной направленности определяет время самого позднего старта и самого позднего финиша для каждого отдельного компонента работы или задачи. Для этого необходимо решить, какова самая поздняя дата завершения проекта. По определению, мы не хотим, чтобы проект длился дольше времени его самого раннего возможного окончания. Растягивать его за этот предел неэффективно.
Нам также не нужно (по крайней мере, сейчас), чтобы проект завершился ранее самого раннего возможного срока его окончания, который высчитан в предыдущих шагах. Если мы хотим завершить проект раньше, придется заново составлять сетевую диаграмму расписания или сокращать сроки некоторых работ (например, направив на них большие ресурсы или повысив производительность труда). Сейчас примем, что все время работ по нашему проекту уборки участка составит 165 минут, и определим это как самый поздний срок окончания проекта.
Если до окончания операции по вывозу мусора должно пройти 165 минут, а сама операция занимает 45 минут, то каков самый поздний срок ее начала? Понятно, что если мы вычтем 45 из 165, то получим 120 минут, что и определяет самое позднее время начала этой операции. Действуя таким же образом, получаем самое позднее время начала упаковки травы в мешки 90 минут, а самое позднее время связывания подрезанных веток — 105 минут. Одно из этих чисел должно быть временем позднего финиша для каждой из предшествующих операций. Какое именно?
Предположим, мы остановимся на 105 минутах. Тогда расписание проекта подскажет нам, что упаковка травы в мешки может начаться самое позднее через 105 минут после начала проекта, поскольку последующие задачи могут решаться только по выполнении предыдущих. Если мы прибавим время, необходимое на упаковку, — 30 минут — к 105 минутам раннего старта, то закончим эту операцию через 135 минут после начала проекта, что больше тех 120 минут, которые были определены ранее. Таким образом, мы превысим срок исполнения проекта, который должен составлять 165 минут.
Следовательно, когда мы производим вычисления расписания по принципу обратной направленности, то самый поздний финиш для предыдущей задачи будет всегда наименьшим среди показателей позднего старта для последующих задач. (Проще говоря, всегда используйте наименьшие числа!)
Теперь посмотрите на сетевую диаграмму расписания, представленную на рис. 9.3. Обратите внимание, что некоторые операции выделены жирным шрифтом. Каждая такая операция имеет одинаковое время раннего старта / позднего старта и раннего финиша / позднего финиша. На этом пути нет резерва времени. По определению, трудовая операция или задача, для которой не предусмотрены временные резервы, называется критической. А вся цепочка таких операций, не имеющих временных резервов, именуется критическим путем (подразумевается, что в случае задержки любой операции на этом пути соответствующим образом изменится и дата окончания проекта). Все те пакеты работ, у которых различное время РС/ПС или РФ/ПФ, располагают определенным временным резервом. Например, в операции по уборке сорняков время раннего старта — 15 минут, а позднего — 60 минут. Таким образом, временной резерв составляет 45 минут.
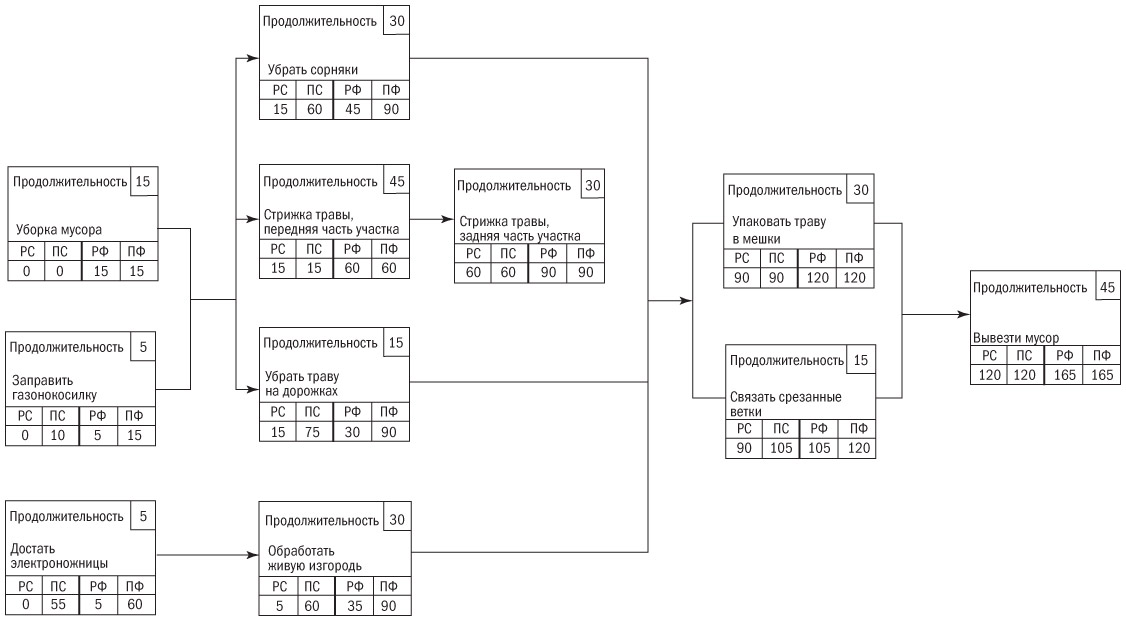
Рис. 9.3. Сетевая диаграмма, показывающая «критический путь»
Окончательный вариант диаграммы сети расписания проекта показан на рис. 9.3. Обратите внимание, что некоторые операции имеют одинаковые показатели РФ и ПФ, так же как РС и ПС. Эти задачи располагаются на критическом пути. На рисунке 9.3 они выделены жирным шрифтом, чтобы наглядно показать их местоположение.
Работы и трудовые операции по проекту, которые находятся на критическом пути, не имеют запасов времени. Они должны быть завершены точно в соответствии с расписанием, или срок исполнения всего проекта превысит 165 минут. Зная, где именно в проекте проходит критический путь, менеджер проекта понимает, на чем конкретно должно быть сосредоточено его внимание. Другие задачи имеют временной лаг. Это не означает, что к их выполнению можно относиться легкомысленно, но они с меньшей вероятностью задержат весь проект, если при их решении возникнут трудности. Например, уборка проросшей на дорожках травы имеет РС 15 минут и ПС 75 минут. Разница между этими показателями составляет 60 минут, что является временным резервом для этой операции.
Что дает нам временной резерв? Как минимум мы знаем, что можем начать выполнение данной операции даже через 75 минут после начала проекта и все же успеем завершить его вовремя. Если вы поручили эту работу своему сыну, то в течение 60 минут он может смотреть телевизор и все равно исполнит задание в срок.
Помните, что все временные показатели — это только оценки. Это означает, что решение той или иной задачи может потребовать больше или меньше времени по сравнению с расписанием. До тех пор пока они выполняются в отрезок времени, отведенный для них расписанием, плюс временной резерв, весь проект может быть завершен в срок. Выполнение критических операций и задач, в которых не имеется временных резервов, следует организовывать таким образом, чтобы уложиться в расписание проекта. Обычно это делается за счет выравнивания ресурсов (или трудовых усилий) либо направлением большего их количества на проект, либо организацией сверхурочных работ.
Это не всегда возможно. Сверхурочные работы нередко приводят к ошибкам и переделкам, что, как правило, не позволяет продвигать проект быстрее, чем по нормальному расписанию. Более того, увеличение числа работников или коллективов, работающих над задачей, часто снижает конечные результаты. На каком-то этапе все участники начинают мешать друг другу, что замедляет, а не ускоряет движение вперед. Обратите внимание на то, что привлечение дополнительных трудовых ресурсов, в том числе и сверхурочные работы, должно использоваться только в случае серьезных проблем. Организовывать работы по проекту так, чтобы это требовало дополнительного рабочего времени, только ради выполнения расписания — не очень хорошая идея.
Еще один чрезвычайно важный момент: всех членов команды проекта следует поощрять к тому, чтобы они рассматривали временные резервы как страховку от неправильных оценок и непредвиденных проблем. Люди склонны затягивать начало выполнения задачи до последнего, а потом, когда возникают проблемы, не справляются со сроками своего пакета работ. Если для данной операции не предусмотрен временной резерв, а ее выполнение занимает больше времени, чем планировалось, это негативно скажется на сроках завершения всего проекта, поскольку, выйдя за пределы временного лага, эта операция попадает на критический путь! По существу, подлинным значением слова «критический» является то, что оно не предусматривает запаса времени. Критическая задача должна быть решена точно в отведенные сроки.
ИСПОЛЬЗОВАНИЕ СЕТЕВЫХ ДИАГРАММ РАСПИСАНИЯ В УПРАВЛЕНИИ ПРОЕКТОМ
Как уже отмечалось, смысл создания диаграмм расписания проекта методом критического пути состоит в управлении проектом. Если управление не возникает, то создание расписания превращается в бесполезное упражнение. Вот несколько правил, которые я использовал в своей работе по управлению проектами.
- Старайтесь придерживаться расписания. Труднее догонять, чем с самого начала равномерно продвигаться к цели.
- Всегда имейте резервное время на случай непредвиденных проблем или неправильных оценок.
- Прилагайте все усилия к тому, чтобы критические операции и задачи выполнялись в соответствии с расписанием. Если какая-то операция или задача могут быть выполнены с опережением графика, добивайтесь этого! Затем переходите к следующей задаче.
- Избегайте соблазна доводить все до совершенства. Оставьте это следующему поколению производителей товаров и услуг. (Примечание: я не сказал, что можно выполнять свою работу спустя рукава или что вы не должны стремиться в ней к наилучшим результатам. Я сказал только, что не стоит поддаваться соблазну перфекционизма. Вы этого не добьетесь никогда.)
- Оценки сроков выполнения тех или иных операций или задач основаны на предположении, что ими будут заниматься конкретные люди. Если вовлекается еще кто-либо, может возникнуть необходимость в соответствующей коррекции сроков. Это в особенности относится к ситуации, когда профессиональная подготовка новичков ниже, чем запланировано в определении человеческих ресурсов.
- Я уже говорил в главе 7, но считаю нужным повторить: ни одна операция или задача в проекте не должна быть рассчитана более чем на 4–6 недель, иначе люди погружаются в ложное ощущение безопасности, откладывая работу и говоря себе: «Я всегда могу начать». Ко времени фактического начала работы они обнаруживают, что уже отстают на несколько дней и не могут закончить ее в соответствии с расписанием. Мы говорим, что они откладывают все усилия на последний отрезок установленного срока. Если выполнение задачи или операции требует более шести недель, полезно разделить их на несколько этапов, установив между ними при необходимости искусственные перерывы. В ходе этих перерывов целесообразно проанализировать достигнутый прогресс. Это позволит держать всю работу нацеленной на конечную цель.
- Если при выполнении своей работы люди не составляют сетевых расписаний, разъясните им их важность и покажите значение временных резервов. Лучше, если вы подготовите для них линейчатую диаграмму работ: ее читать гораздо проще, чем сетевую. Объясните коллегам, что если они выходят за рамки временных резервов по операции, то следующие этапы могут стать критическими, создавая большой стресс для тех сотрудников, которым предстоит их выполнять.
- Сократить сроки можно путем добавления ресурсов, уменьшения содержания, снижения качества работ, а также изменения процесса их выполнения. За исключением снижения качества работ, все эти пути вполне приемлемы. Уменьшение содержания работ, разумеется, должно быть оговорено с клиентом или заказчиком.
- Процесс разработки расписания проекта изначально предполагает, что в вашем распоряжении будут все запланированные ресурсы. Если вы одновременно со своим проектом направляете сотрудников на другие или планируете задействовать одного и того же человека на нескольких операциях, дело может кончиться перегрузкой людей. Современное программное обеспечение обычно предупреждает о подобных коллизиях и подсказывает выход из положения.
ПЕРЕВОД СТРЕЛОЧНЫХ ДИАГРАММ В ЛИНЕЙЧАТЫЕ
Хотя стрелочные диаграммы и важны для правильного анализа взаимосвязи между отдельными работами и операциями в проекте, линейчатые диаграммы Гантта представляются мне более удобными. Подчиненные сразу понимают, когда им следует начать работу, а когда — закончить ее. Стрелочная (сетевая) диаграмма на изображена как линейчатая диаграмма на рис. 9.4. При этом мы пользуемся тем, что узнали о расписании проекта из анализа сетевой диаграммы.
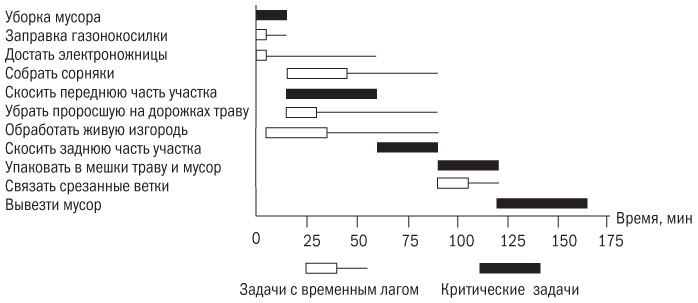
Рис. 9.4. Линейчатая диаграмма расписания проекта по уборке участка
Обратите внимание на то, что критический путь на этой диаграмме представлен черными прямоугольниками. Белые прямоугольники пустые, возле них имеются линии, указывающие на временной резерв. Выполнение задачи может закончиться самое позднее в месте окончания линий.
Это удобно. Компьютерные программы позволяют создать линейчатые диаграммы, способные показать критический путь и временные лаги. Одно предупреждение: многие программы изображают критический путь на цветных мониторах красным. А стартовавшие работы или операции — зеленым или синим. При распечатке на черно-белых принтерах все строки выглядят черными, а это подразумевает, что все операции критические, и вводит в заблуждение людей, читающих диаграммы. Лучше придать разным строкам разные оттенки серого или пометить критические пути крестиками или другими знаками, чтобы избежать двусмысленности.
ОБЕСПЕЧЕНИЕ ПРОЕКТА РЕСУРСАМИ
Я уже говорил, что первый шаг в разработке расписания — предположение, что ресурсы неограниченны. Это самая благоприятная ситуация. Но если вы думаете, что проект может быть выполнен в срок, нужно проверить, насколько ваше предположение о неограниченных ресурсах соответствует реальности.
Скорее всего, вы сразу же увидите, что одни и те же люди выполняют в вашем расписании одновременно по две-три операции, что обычно невозможно. Такие перегрузки ресурсов можно разрешить с помощью компьютерных программ, если только речь не идет о совсем простых расписаниях. Здесь компьютерные технологии действительно помогают, однако, по имеющимся данным, мало кто реально использует их для выравнивания необходимых проекту ресурсов.
Посмотрите на расписание на рис. 9.5. Оно включает в себя всего четыре задачи. Две из них критические, а две имеют временные резервы. Для выполнения в течение трех недель задачи А необходимы два работника. Задачи Б и В требуют по одному работнику каждая. Однако когда подходит время для исполнения проекта, вы обнаруживаете, что у вас всего три работника. Как это произошло?
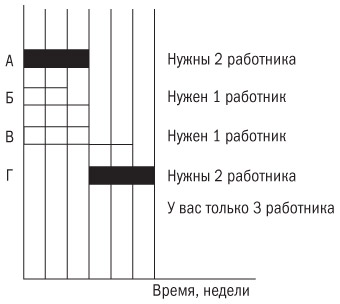
Рис. 9.5. Расписание с перегруженными ресурсами
Вполне вероятно, что для данного проекта не было возможности выделить более трех исполнителей. Но поскольку вы следовали правилу «параллельных задач», которые логически могут выполняться параллельно, вы неизбежно перегрузили своих сотрудников. Не исключено, что на момент составления расписания можно было задействовать четырех человек, однако впоследствии одного из них перевели на другой, приоритетный проект.
В любом случае это расписание не будет работать до тех пор, пока в него не внесут какие-либо изменения. Все возможные изменения располагаются в трех областях. Прежде всего следует уточнить, есть ли у какой-то из запланированных операций временной резерв, который позволяет задержать старт до получения необходимых ресурсов. Оказывается, что в данном случае это возможно (рис. 9.6).
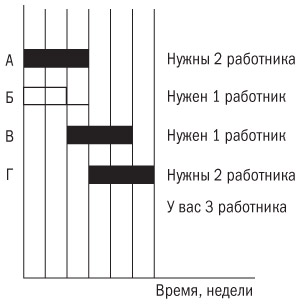
Рис. 9.6. Расписание, в котором резервы времени используются для выравнивания ресурсов
Конечно, здесь это образцовое решение из учебника прекрасно работает. В реальной жизни все не так просто. Обратите внимание, что задача В имеет достаточный временной лаг, чтобы «подождать», пока закончится выполнение операции Б. Однако в обычной жизни нередко временной лаг операции В заканчивается до завершения операции Б. Кроме того, операция Г, скорее всего, потребует задействовать трех работников, а не двух. Это серьезно усложняет ситуацию (рис. 9.7).
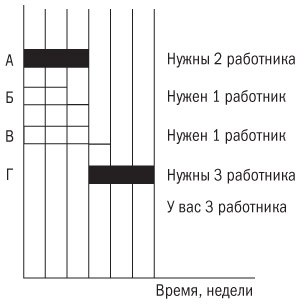
Рис. 9.7. Расписание с недостаточным временным резервом по операции В для выравнивания ресурсов
Поскольку подобные ситуации в жизни встречаются весьма часто, мы должны быть готовы разрешать их. Есть еще два возможных источника помощи. Первый — функциональная связь между переменными:
Стоимость = f(x) (Результат, Сроки, Содержание).
Задайте себе вопрос, можно ли уменьшить содержание проекта, изменить сроки или понизить результат, то есть качество. Последнее обычно даже не обсуждается, но другие параметры подлежат рассмотрению. Например, иногда можно уменьшить содержание, и результат все равно останется приемлемым для заказчика. Разумеется, если привлечь к какой-то работе или операции другого человека хотя бы на короткое время, то вам не придется думать об уменьшении объема проекта. Выбирайте сами.
Вы спрашиваете менеджера, распоряжающегося ресурсами, может ли он дать вам дополнительного человека. Тот с грустью отвечает, что не может и даже подумывал забрать у вас одного из ваших троих. Каким-то образом вам удается убедить его не делать этого. Затем вы спрашиваете спонсора проекта, можно ли уменьшить его содержание. Ответ отрицательный.
Недопустимо и снижение качества. И вы не можете найти ни одного стороннего работника, которого можно было бы привлечь по контракту. Вы между Сциллой и Харибдой. Вы начинаете думать, не существует ли какого-то другого производственного процесса или трудовой операции, которые помогут вам выполнить работу. Например, если использовать для покраски поверхностей краскопульт вместо валика, задача решится гораздо быстрее.
Предположим, вы попробовали и это и снова ничего не получилось. Вы решаете: единственное, что осталось, — это отказаться от работы. Ведь вы никогда не хотели быть руководителем проекта. Подождите. Может быть, можно еще кое-что предпринять?
Вспомните, что я уже говорил. Вы используете все временные резервы, имеющиеся у операции В, и теперь она становится частью критического пути. Когда вы даете своей программе задание выровнять ресурсы, она требует данных о том, планируете ли вы расписание с учетом доступного для операции В временного лага. Если вы говорите «да», то, как только временной резерв по данной операции заканчивается, вы не сможете двигаться вперед. Это называется критическим по отношению ко времени выравниванием ресурсов, поскольку время — это суть вашего проекта. (И всегда является таковым!)
Однако предположим, что вы отвечаете «нет» на вопрос «Хотите ли выровнять ресурсы в пределах существующего временного лага?». В этом случае вы приказываете программе продолжить отодвигать начало выполнения операций до тех пор, пока ресурсы по проекту не станут достаточными, даже если это предполагает отдаление даты окончания проекта. (Это называется критическим выравниванием ресурсов.) Если вы попробуете сделать это на нашем расписании, то придете к решению, которое показано на рис. 9.8. Не так плохо, если только вы в состоянии переносить задержки.
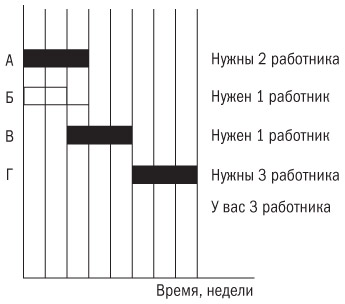
Рис. 9.8. Расписание проекта с критическим выравниванием ресурсов
Однако в некоторых случаях задержки настолько вредны, что выглядят даже смешными. Ваш проект должен быть закончен в декабре текущего года. А компьютер показывает, что ему настолько не хватает ресурсов, что он может быть завершен только в конце 2019 года! Смешно! Какой толк от таких дальних планов?
Такой метод можно использовать для того, чтобы обратить внимание участников проекта на существующие проблемы. Он демонстрирует возможный негативный эффект недостаточности ресурсов и заставляет искать компромиссные решения, которые уже были описаны, при всеобщем понимании, что выполнение расписания проекта — высший приоритет. Я общался с одним человеком, который заявлял, что не верит в приоритетность расписаний, поскольку все они нереальны. Нереальное расписание, составленное на основе красивых вычислений, ничего не доказывает.
До некоторой степени это правда. Однако если вы хотите осознать ограничения, с которыми мы сталкиваемся при планировании проекта, нужно хотя бы с ними познакомиться. Каждый должен понимать, что оценки — всего лишь предположения. То же самое относится к прогнозам рынков и погоды, которые, как известно, не могут похвастаться блестящими результатами. Более того, как уже отмечалось, все работы и операции подвержены изменениям. Если вы не понимаете этого, то вместо работы управляющего проектом вам лучше присмотреть что-либо другое.
РЕСУРСНОЕ ОБЕСПЕЧЕНИЕ
Важнейшим фактором распределения ресурсов проекта является правильный учет способности каждого человека выполнять свою работу. Инженеры в промышленности обычно исходят из того, что ни один работник не может уделять собственно работе больше 80% своего рабочего времени. При восьмичасовом рабочем дне это 6,4 часа. С учетом здоровой предусмотрительности реально это шесть часов. 20% потерянного рабочего времени распределяются на три фактора, называемых ЛУЗ: Л — факторы личного порядка (любому работнику нужны перерывы, вызванные физиологическими причинами); У — фактор усталости (производительность труда людей снижается по мере накопления усталости); З — фактор задержек (люди теряют время в ожидании рекомендаций коллег, поставки комплектующих и деталей или указаний со стороны руководства).
Опыт показывает, что даже уровня в 80% достигают только те, кто привязан к своему рабочему месту. Это относится прежде всего к людям, занятым физическим трудом, или тем, кто выполняет достаточно однообразные операции, например к сотрудникам страховых компаний, которые принимают заявления по страховым случаям (но даже они время от времени передвигаются по помещению). Что касается работников интеллектуального труда, нельзя ожидать, что они посвятят 80% своего рабочего времени продуктивной работе. Этот показатель обычно ближе к 50%, а то и ниже! В одной компании, занимающейся проектами, провели эксперимент, в ходе которого люди фиксировали свои занятия через каждые два часа в течение двух недель. В результате оказалось, что собственно работа над проектами составила только 25% их рабочего времени. Остальное ушло на совещания, сопутствующие операции, старые проекты, которые были завершены прежде и теперь поступили для анализа к разрабатывавшим их работникам, составление бюджетов на следующий год, работу с заказчиками и так далее.
Большинство специальных компьютерных программ позволяют определить количество рабочих часов, необходимых для выполнения той или иной операции или задания, а также процентную долю рабочего дня исполнителя. Программа сама переводит эти оценки в календарную форму. То есть, например, если привлеченный на половину рабочего дня работник выполняет операцию, на которую необходимо 20 рабочих часов, то закончить ее он сможет только через неделю (или больше).
В управлении проектами особенно важно реально представлять себе возможности исполнителей. В противном случае ваши расписания будут даже хуже, чем бесполезными. Я говорю «хуже», потому что они будут короткими и ошибочными и только нанесут вред вашей компании. Тщательно изучите реальное время, которое сотрудники затрачивают на свою работу, и только после этого приступайте к расчету расписания. А если людям не нравится, что они много времени тратят на действия, не связанные с проектом, исключите необходимость таких действий.
Исполнителей нередко заставляют работать сверхурочно, чтобы выполнить всю работу по проекту, в которую в течение дня вклинивались различные отвлекающие моменты. Между тем исследования однозначно доказали: сверхурочная работа чрезвычайно негативно влияет на производительность. Так что это заведомо проигрышная тактика. Можно еще допустить небольшие переработки, но длительные и постоянные сверхурочные работы способны создать для компании серьезные проблемы.
РЕЗЮМЕ
- Начиная разработку расписания, исключите возможность ограничения проекта в ресурсах.
- Критический путь — самый длинный отрезок проекта, не имеющий временных резервов. Обратите внимание на то, что в некоторых проектах самые продолжительные операции или работы не являются критическими, поскольку имеют временной лаг.
- Никто не в состоянии обеспечить продуктивную работу на протяжении более 80% продолжительности рабочего дня.
УПРАЖНЕНИЕ
В диаграмме сети расписания рассчитайте ранние и поздние старты и финиши, а также временные резервы для некритических операций. Какие из этих операций формируют критический путь? Ответы — в разделе в конце книги.
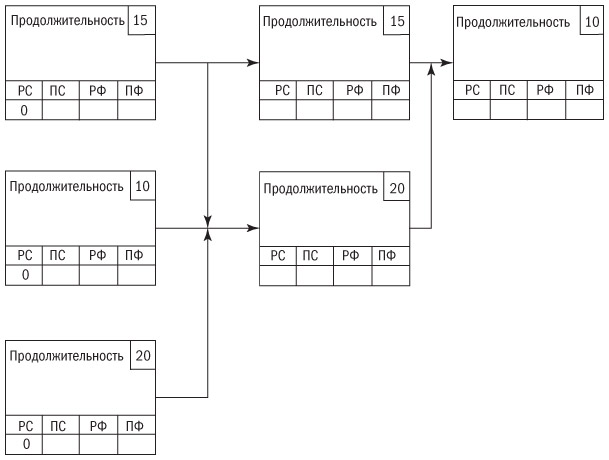
Рис. 9.9. Диаграмма сети расписания в качестве упражнения

