Для нас очевидно, что все цифры сотворены равными. Нет, мы не имеем в виду «равными друг другу» – разумеется, нет! Но внутри нас теплится вера в то, что все десять цифр, от 0 до 9, играют одинаковые роли в мире чисел.

Печальная правда заключается в том, что числа могут быть такими же нескромными, как люди: они все стремятся к первенству. Представьте, что вам приглянулась вещь стоимостью 43,52 доллара. Какая из цифр кажется вам более значимой? Важнее всего для вас цифра четыре, а двойка на конце не играет почти никакой роли. Вы встревожитесь, если четверка вдруг изменится на девятку, а если изменится двойка, вряд ли вас это сильно взволнует.

Тот, кто ждет от Вселенной справедливости, должен верить, что у всех цифр одинаковые шансы сыграть значимую роль, – но бедный, бедный нолик! Он не становится первой значащей цифрой, честь выпала на долю других. Все они стремятся быть значительней остальных настолько часто, насколько это возможно.

Мы верим, что цифры от 1 до 9 участвуют в математике на равных правах и каждая начинает одну девятую часть всех существующих чисел (примерно 11 %). Разумеется, не может быть большего количества чисел, начинающихся с двойки, чем с пятерки.

Ведь так?

Утверждение о том, что все цифры от 1 до 9 равно представлены в качестве первой значащей цифры, приобретает смысл, если иметь в виду определенный диапазон чисел: скажем, от 1 до 999 999. В этом случае все цифры от 1 до 9 одинаково часто занимают место первой значащей цифры.

Разумеется, на результат влияет, какой именно диапазон мы выбрали. Если мы посмотрим на другой ряд чисел, скажем от 1 до 19, то обнаружим, что здесь все цифры от 2 до 9 занимают первую позицию всего единожды, в то время как 1 становится первой значащей цифрой в 11 случаях.

Ради беспристрастности давайте возьмем какие-нибудь величины из внешнего мира. Мы должны быть аккуратными и не искать числа, сконцентрированные в узком диапазоне. Поэтому мы не станем брать такой параметр, как рост взрослого человека, ведь практически все результаты измерений будут начинаться с 1 или 2 (ничтожно малое количество людей имеет рост выше 299 или ниже 100 сантиметров).

Ради уверенности в том, что все цифры имеют одинаковые шансы стать первой значащей цифрой числа, мы будем вести измерения в широком диапазоне. Например, давайте зададимся вопросом, насколько велико население разных стран. Это значение будет колебаться от миллиарда с лишним (Китай и Индия) до менее чем десяти тысяч (в случае с карликовым государством на коралловом острове Науру). Вдобавок к численности населения давайте выясним следующие параметры для сотен государств:

– валовой внутренний продукт (в долларах США);

– количество аэропортов;

– площадь (в квадратных километрах);

– ежегодную выработку электроэнергии (в киловатт-часах);

– ежегодное потребление продуктов нефтепереработки (в баррелях);

– общую длину всех железных дорог (в километрах);

– количество телефонов.

Таким образом, мы соберем около 2000 параметров и затем подсчитаем, сколько чисел начинается с цифры 1, сколько – с цифры 2 и т. д. Вот что у нас получится:

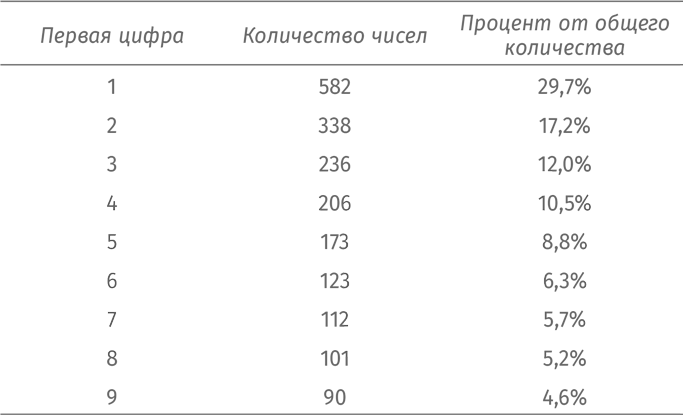
Невероятно: чаще всего на первой позиции встречается цифра 1 (примерно в 30 % случаев) и реже всего – цифра 9 (меньше 5 % случаев)!

Мы призываем читателей повторить эксперимент самостоятельно: взять статистический справочник, выписать первые цифры длин рек, высот гор, курсов акций, среднего роста различных видов животных, количества слов в романах, производства риса в разных странах и т. д.

Соберите как можно больше параметров, покрывающих широкий диапазон значений, и вы увидите все ту же логику. Чаще всего первой цифрой оказывается единица, реже всего – девятка.

Такое неравномерное распределение первых значащих цифр известно как закон Бенфорда, названный в честь Фрэнка Бенфорда. Он опубликовал статью об этом феномене в 1938 году, хотя необходимо отметить, что еще в 1881 году к такому же выводу пришел Саймон Ньюком.

Закон Бенфорда утверждает нечто большее, чем «единица на первой значащей позиции встречается чаще всего, а девятка – реже всего». Закон Бенфорда констатирует (при наличии большого количества данных) следующую частотность:

Есть и другая область, где обнаруживается неравномерное распределение первых значащих цифр, – это знакомая всем таблица умножения:

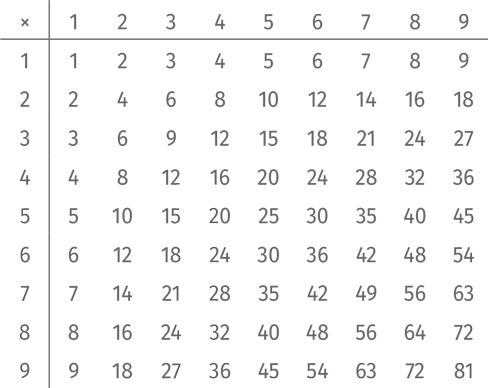
Среди 81 числа в этой таблице 18 начинаются на 1, а именно:

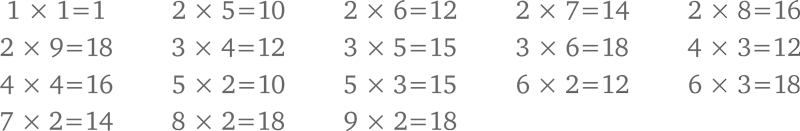
При этом всего 3 числа начинаются на 9:

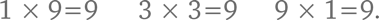
Вот процентное соотношение первых значащих цифр в обычной таблице умножения.

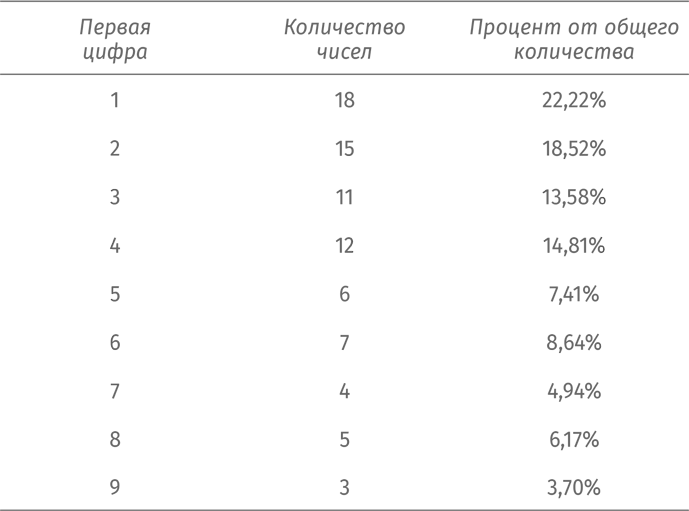
Мы видим, что цифры поменьше встречаются чаще, чем цифры побольше, но частотность здесь не совсем такая, какую предсказывает закон Бенфорда.

Таблица умножения дает нам все возможные результаты умножения одного однозначного числа на другое от 1 × 1 до 9 × 9.

Давайте расширим этот принцип и переберем все варианты умножения трех однозначных чисел. Проделаем следующие вычисления:

В общей сложности это дает 9³ = 729 троек. Посмотрим, как часто встречаются разные цифры в первой позиции:

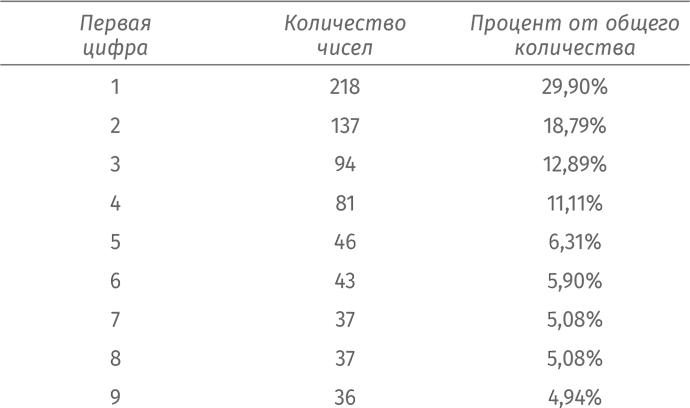
Нет резона останавливаться на перемножении трех чисел. Мы можем составить четырехмерные, пятимерные, шестимерные таблицы умножения и т. д. Давайте сразу посмотрим, что получится с десятимерной таблицей умножения. Она содержит все возможные комбинации произведений десяти чисел от 1 до 9. Другими словами, мы проделываем следующие вычисления:

Занесем в таблицу, как много чисел начинается с 1, 2 и т. д.:

Мы увидим, что частотность первых цифр в этом случае уже хорошо согласуется с законом Бенфорда.

Перед тем как вникнуть в детали закона Бенфорда, давайте обратим внимание на одно его практическое применение.

Предположим, некий нечистый на руку человек подделывает налоговые декларации (меняет суммы, фабрикует баланс и т. д.). Короче говоря, он лжет и выдумывает числа, не имеющие отношения к реальности. Начальные цифры он выбирает случайным образом.

Судебный эксперт может быстро проверить, совпадает ли распределение первых цифр с законом Бенфорда. Если не совпадает, возникают подозрения, что числа подделаны. Но это еще не строгое доказательство вины.

Сверхбольшие и сверхмалые числа удобно записывать в экспоненциальном виде. Например, число 12 300 000 в экспоненциальном представлении выглядит так: 1,23 × 10⁷. Мы записываем число от 1 до 10, умноженное на степень 10. Основное число называется мантисса. Например, мантисса 853 100 000 равна 8,531:

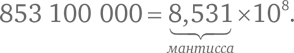
По определению, мантисса не может быть меньше одного и не может быть больше или равна десяти: 1 ≤ мантисса < 10.

Мантисса поможет нам сформулировать усовершенствованный вариант закона Бенфорда. Грубо говоря, закон гласит, что среди большого количества измерений около 30 % чисел имеют первую значащую цифру 1, то есть имеют мантиссу меньше 2.

Уточняя закон Бенфорда, мы можем присмотреться к первым двум цифрам большого количества измерений и задаться вопросом: с какой частотой мантисса будет, скажем, меньше 1,7? Вот другая формулировка того же вопроса: с какой частотой первые две цифры будут 10, 11, 12, 13, 14, 15 и 16?

В более общем виде: для любого числа m между 1 и 10 мы обозначим f(m) долю чисел, чья мантисса меньше m.

Например, f(2) – доля чисел, начинающихся на цифру 1. Величина f(3) означает долю чисел с начальной цифрой 1 и 2. Такая запись поможет понять, как возрастают частоты в законе Бенфорда.

Как использовать такую форму записи для обозначения доли измерений с начальной цифрой, скажем, 4?

• Заметим, что запись f(4) не означает, что начальная цифра равна 4. Это может быть также 1, 2 или 3.

• Точно так же запись f(5) означает, что первые цифры могут быть 1, 2, 3, 4.

• Чтобы выяснить, сколько чисел начинается на цифру 4, вычтем одну величину из другой: f(5) – f(4). Тогда мы исключим числа с начальной цифрой 1, 2, 3.

Есть две особые величины: чему равно f(1) и f(10)? Подумайте минуту, прежде чем читать дальше.

Вспомним: f(m) обозначает долю чисел с мантиссой меньше m. В то же время 1 ≤ m < 10. Что из этого следует?

• Нет ни одного числа с мантиссой меньше 1. Таким образом, f(1) = 0.

• Мантиссы всех чисел меньше 10. Таким образом, f(10) = 1 (или, если вам угодно, 100 %).

Между этими границами величина f(m) возрастает. Чем больше чисел с мантиссой меньше m, тем больше f(m).

Следующий шаг – понять, как f(m) зависит от m. Но вначале мы рассмотрим общий случай перехода из одной единицы измерения в другую.

Мы собрали тысячи измерений длин в километрах и увидели закон распределения первых цифр. Если мы переведем километры в мили, распределение не изменится. Измерения внутреннего валового продукта в долларах США дают примерно такую же частотность первых цифр. Ничего не изменится, если мы будем измерять ВВП в евро (или британских фунтах, или российских рублях). Но давайте присмотримся к переводу ярдов в футы.

Предположим, мы измеряем огромное количество расстояний в ярдах и в футах и изучаем распределение первых цифр. Как много величин имеют первую значащую цифру 2? Это множество включает и 2,1, и 28, и 0,213, и 299,8 ярда. В обозначениях, которые мы приняли в предыдущем разделе, доля величин такого рода по отношению ко всем измерениям равна f(3) – f(2).

А теперь переведем наши измерения в футы. Иными словами, просто умножим всё на 3. 2,1 ярда равны 6,3 фута. Измерения в ярдах с первой значащей цифрой 2 превратятся в измерения с первой значащей цифрой от 6 до 9, не включая 9. Вы удивлены?

Вначале может показаться, что, если первая значащая цифра величин в ярдах равна 2, первая значащая цифра величин в футах будет равна 6. Это не так: 2,8 ярда равны 8,4 фута. Если мантисса измерений в ярдах находится в пределах от 2 до 3 (не включая 3), мантисса тех же измерений в футах будет в пределах от 6 до 9 (не включая 9).

Какая доля измерений имеет первую значащую цифру 6, 7 или 8? Ответ: f(9) – f(6).

Близится кульминация: мы имеем дело с одними и теми же измерениями в разных единицах длины, поэтому доля измерений в ярдах с мантиссой 2 будет равна доле измерений в футах с мантиссой 6, 7 или 8. Иными словами, f(3) – f(2) в ярдах равно f(9) – f(6) в футах. Посмотрите на рисунок. Оба прямоугольника символизируют всю совокупность наших измерений: первый прямоугольник – в ярдах, второй прямоугольник – в футах. Серая область в первом прямоугольнике обозначает измерения с мантиссой 2. Соответствующая область во втором прямоугольнике обозначает измерения с мантиссой 6, 7 или 8.

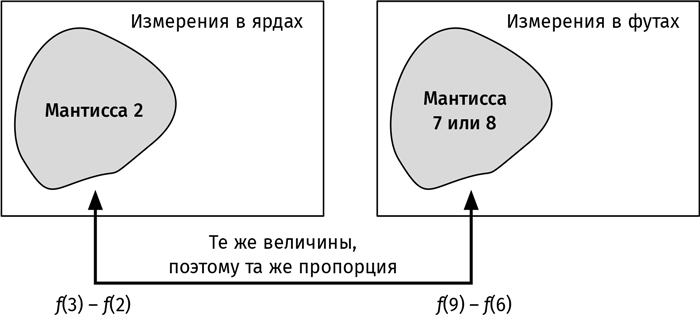
Важно понимать, что обе закрашенные области идентичны! Так что доля измерений в ярдах с мантиссой 2 равна доле измерений в футах с мантиссой 6, 7 или 8.

Рассмотрим более общий случай. Вообразим, что мы собрали множество измерений и хотим выяснить, сколько из них имеют мантиссу меньше определенного числа a. Доля величин, удовлетворяющих этому условию, равна f(a).

Мы переводим результаты в другие единицы измерения. Пусть коэффициент будет равен числу b. Иными словами, если длина объекта в одних единицах измерения равна 23,5, в других она будет равна 23,5 × b.

Напомню, что f(a) равно доле величин с мантиссой от 1 до a, не включая a. Те же величины в других единицах имеют мантиссу строго меньше ab. Их доля равна f(ab).

На языке формул тезис о равенстве долей величин с мантиссой меньше a в одних единицах и с мантиссой меньше ab в других единицах выглядит так:

Или:

Новый вопрос: какого рода функция удовлетворяет этому правилу и условиям f(1) = 0 и f(10) = 1?

Некоторые математические операции можно проделать наоборот. Например, мы возводим в квадрат какое-нибудь число: 6² = 36. А теперь проделываем обратную операцию – извлекаем квадратный корень: Для положительных чисел операции возведения в квадрат и извлечения квадратного корня обратны друг другу. Операция, обратная возведению в степень, называется извлечением логарифма.

Например, 10⁴ = 10 000. Мы проделываем наоборот операцию возведения в степень и применяем логарифмическую функцию:

Можно воспринимать логарифмическую функцию как ответ на вопрос: «В какую степень возводить?» В какую степень нужно возвести 10, чтобы получить некое число? Скажем, какая степень 10 дает 1000? Поскольку 1000 = 10 × 10 × 10 = 10³, ответ равен 3. Иными словами, lg(1000) = 3.

Несложно уяснить, что происходит, когда мы возводим 10 в степень, равную целому положительному числу, – мы просто перемножаем 10 заданное число раз:

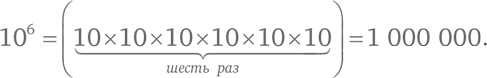
Если мы посчитаем нули в одной из степеней 10, то поймем значение логарифма:

Возведение 10 в дробную степень несколько сложнее. Ключевая идея здесь – понять, чему равно произведение 10^m и 10ⁿ.

Чему равно произведение 10⁶ × 10⁵? Не бойтесь, перемножать десятки просто. Давайте распишем нашу формулу:

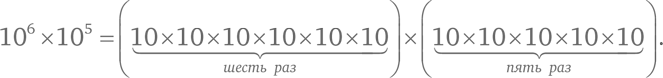
Каков результат? Нет нужды перемножать! Просто посчитайте, сколько раз встречается 10 в правой части формулы: одиннадцать. Иными словами,

Таким образом, для целых положительных степеней

Это тождество называется законом умножения степеней.

Ключевая идея вычисления дробной степени – применение данного закона для любых показателей степени. Давайте посмотрим, к чему это приведет.

Возьмем 10^0,5. Мы можем не знать, чему оно равно, но нам известно, чему равно произведение 10^0,5 × 10^0,5. А именно:

Если умножить 10^0,5 само на себя, получится 10. Таким образом, 10^0,5 равно квадратному корню из десяти:

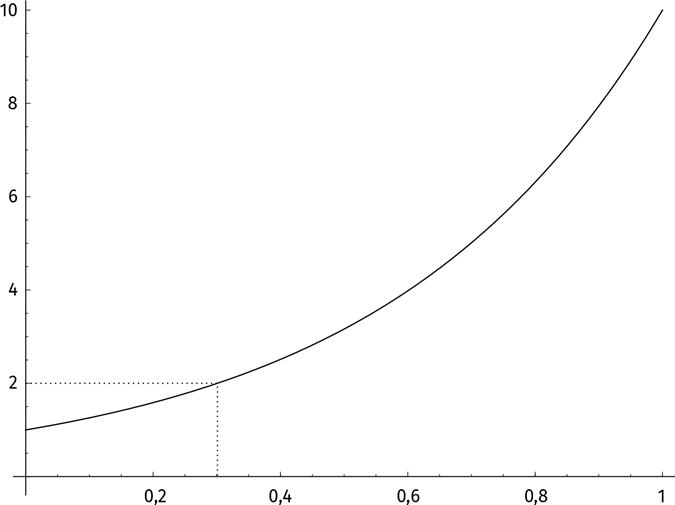
Так мы можем посчитать все степени 10. На рисунке вы видите график функции 10^х при x от 0 до 1.

При каком значении x выполняется условие 10^х = 2? При взгляде на график функции 10^х кажется, что подойдет x = 0,3. Если мы возьмем калькулятор, то выясним: 10^0,3 ≈ 1,99526… Близко, но не равно точно 2. Чуть-чуть увеличим степень. Попробуем x = 0,301; результат 10^0,301 ≈ 1,99986… Ближе, но все еще мимо цели. Нам нужно число немного больше. Величина x должна быть равна 0,30102999566398114… Это и будет log(2). (Вы уже встречали такое число раньше. Отыщите его!)

Закон умножения степеней 10^m × 10ⁿ = 10^{m +} ⁿ можно переформулировать для логарифмов. Посмотрим, как такое сделать. Допустим, a = 10^m и b = 10ⁿ.

Чему равен десятичный логарифм a? Это степень, в которую нужно возвести 10, чтобы получить a. Иными словами, lg(a) = m. Аналогично lg(b) = n.

Чему равен логарифм произведения ab? Мы знаем, что a = 10^m и b = 10ⁿ. Таким образом, ab = 10^{m +} ⁿ. В какую степень нужно возвести 10, чтобы получить ab? Ответ: m + n. На языке математических символов это выглядит так: lg(ab) = m + n.

Подытожим:

Отсюда мы выводим закон сложения для логарифмов:

Похоже, мы уже встречали эту формулу…

Давайте подытожим то, что мы узнали из предыдущих разделов. Мы определили функцию f(m) как долю тех величин среди большого количества измерений, мантисса которых меньше m. Эта функция удовлетворяет трем условиям:

Потом мы обсудили логарифмы и выяснили следующее:

Другими словами, значения f при 0 и 10 совпадает со значением десятичного логарифма от тех же величин. Кроме того, f и логарифм подчиняются одному и тому же правилу в соответствии с формулами (*) и (**). На основе этих фактов (и чисто технической оговорки, что функция f непрерывна) математики могут доказать, что f представляет собой логарифмическую функцию.

Теперь мы наконец готовы указать точную частотность первых значащих цифр при большом количестве измерений.

Какая доля измерений имеет первую значащую цифру 1? Сформулируем вопрос иначе: какая доля этих величин имеет мантиссу меньше 2? Ответ равен f(2) = lg(2) ≈ 0,3010 = 30,1 %.

Какая доля величин начинается с 9? Ответ равен f(10) – f(9), так как мы должны вычесть из общего количества величин те, первая значащая цифра которых меньше 9.

Это дает f(10) – f(9) = lg(10) – lg(9) ≈ 1 – 0,9542 = 0,0458 = 4,58 %.

Когда-то я задавал вопрос о значении f(1,7). Теперь можно уверенно ответить: