Глава 7
e
Леонард Эйлер
Когда твоим именем называют число, это ли не величайшая честь для математика? Швейцарец Леонард Эйлер жил в XVIII веке, и в главе 7 мы поговорим о числе Эйлера. Его обозначают буквой e.
Число Эйлера можно задать разными способами, но стандартным считается следующий:
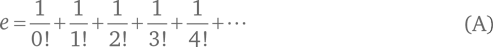
Этот ряд уходит в бесконечность. Восклицательными знаками обозначен факториал. Для положительного целого числа n факториал считают по такой формуле:
n! = n × (n – 1) × (n – 2) × (n – 3) × … × 2 × 1.
Например, 4! = 4 × 3 × 2 × 1 = 24. Факториал нуля равен 1. Вы можете узнать о факториале больше в главе 10.
Достаточно сделать всего несколько шагов по приведенному выше алгоритму, чтобы вычислить e c хорошей точностью. Когда мы дойдем до 1/10! сумма будет равна
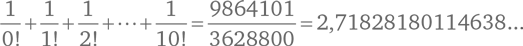
Это довольно близко к более точному значению 2,718281828459045…
Число Эйлера повсеместно встречается в разных областях математики. Далее я покажу вам три совершенно разные задачи, для решения которых нужно e.
«Прибыльное» число
Банк выдает депозитный сертификат на десять лет. Когда этот срок истекает, вклад удваивается. Если ваш вклад составляет 1000 долларов, через десять лет вы получите 2000 долларов. Рост ваших инвестиций составляет 100 %. Не исключено, что для банка выгоднее выплачивать 10 % ежегодно, а не 100 % спустя десять лет.
Банк может выдать еще более привлекательный сертификат, позволяющий вам получать прибыль ежегодно и снова класть ее на депозит. Посмотрим, как это отразится на ваших финансах.
Начнем с 1000 долларов. В конце года вы получите 100 долларов. Теперь у вас 1100 долларов. На следующий год ваша прибыль возрастет. Банк выдаст вам уже не 100 долларов, а 10 % от 1100, то есть 110 долларов. Теперь у вас 1210 долларов. На третий год банк выдаст 10 % от этой суммы. Посмотрим, какую прибыль вы будете получать год от года и насколько станет увеличиваться ваш вклад:
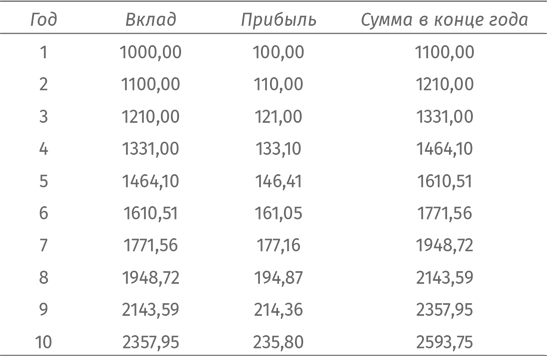
Вначале у вас было A долларов. В первый год прибыль составила 10 %. В конце года вы получили 1,1 × A. На второй год 1,1 × 1,1 × A. Несложно увидеть, что в конце десятого года у вас на руках окажется
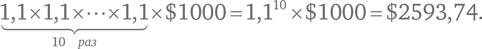
Это близко к нашим недавним расчетам. Таким образом, новый депозитный сертификат оказывается существенно выгоднее – денег становится больше не в 2, а почти в 2,6 раза.
А что произойдет, если банк начнет выдавать прибыль раз в три месяца, а не ежегодно? Если за год выручка составляет 10 %, то за три месяца набегает 2,5 %. В первом квартале ваша доход составит 0,025 × 1000 = 25 долларов. Общая сумма будет равна 1,025 × 1000 = 1025 долларов. В конце второго квартала вы получите уже 0,025 × 1,025 = 25,63 доллара (если округлить до сотых). Теперь у вас 1,025 × 1025 = 1050,63 доллара.
Спустя N кварталов ваша 1000 долларов увеличивается следующим образом:
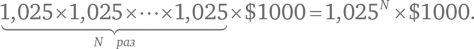
Подставим N = 40 (поскольку в 10 годах 40 раз по 3 месяца) и увидим, что депозитный сертификат принес 2685,06 доллара.
В первом случае деньги удвоились. Во втором сумма выросла в 2,59 раза. В третьем – в 2,69 раза. А что произойдет, если требовать прибыль ежемесячно, сохраняя условие, что деньги можно тут же снова класть на счет? А еще лучше – ежедневно?
В случае ежемесячных выплат вы станете получать 10/12 %. Если в начале месяца у вас на руках была сумма A, в конце месяца она вырастет:
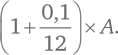
Спустя N месяцев вы получите:
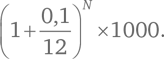
Если N = 120, ваша итоговая сумма составит 2707,04 доллара.
Число дней в високосном году больше, чем в обычном, но для упрощения вычислений давайте примем за данность, что длительность каждого года 365 дней. За день вы будете получать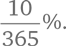 
Спустя N дней общая сумма составит:
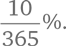Спустя N дней общая сумма составит:
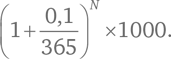
Если N = 3650, вы будете обладать суммой в 2717,91 доллара.
А что, если вам и этого мало? Что, если вы потребуете от банка платить вам ежечасно?.. ежеминутно?.. ежесекундно?
В году 31 556 926 секунд, так что спустя 10 лет у вас будет:
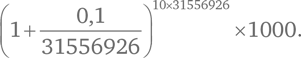
Это дает 2718,28 доллара.
Подытожим:
А зачем останавливаться на секундах? Пусть банк выплачивает вам деньги каждую миллисекунду или наносекунду. Впрочем, это не изменит общей суммы. Вы все равно получите те же 2718,28 доллара, потому что вынуждены округлять до центов.
В пределе вы достигнете непрерывных выплат. Если посчитать всю сумму в точности, банк должен будет отдать вам 1000 × e долларов!
Непрерывные выплаты – пример экспоненциального роста. Пусть A – начальное число (денег, микробов и т. д.). Оно вырастает со скоростью r на протяжении периода времени t. Если новое число вырастает с той же скоростью и этот рост непрерывный, то в конце мы получим:
Aert,
где e – знакомое нам число Эйлера. В нашем примере A = 1000 (первоначальный вклад), r = 0,1 (процентная ставка), t = 10 (количество лет). В конце мы имеем 2718,28 доллара.
Процесс может быть и обратным, когда нечто непрерывно убывает. Тогда в конце мы получим Ae–rt.
Переполох со шляпами
В одном городе был театр. Его посетители на время представления сдавали шляпы в гардероб, а потом забирали обратно.
Однажды гардеробщик – то ли он выпил лишнего, то ли просто свихнулся – стал выдавать шляпы не по номеркам, а в произвольном порядке. Вопрос: какова вероятность того, что никто не получит свою шляпу?
Сформулируем вопрос точнее. В театр пришло N зрителей. Они встают в очередь за шляпами. Сумасшедший гардеробщик выдает шляпы в произвольном порядке. Таким образом, шляпы могут быть выданы N! различными вариантами. Все они равновероятны. Это математическая формулировка выражения «в произвольном порядке».
Разберем случай N = 4. Укажем в таблице все варианты выдачи шляп и пометим стрелочкой те случаи, когда ни один из зрителей не получает свою шляпу.
В 9 случаях из 24 никто не получает свою шляпу. Таким образом, при N = 4 интересующая нас вероятность равна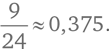 
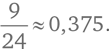
Для N = 5 существует 5! = 120 различных вариантов вернуть шляпы. Из них 44 нам подходят: ни один человек не получит свою шляпу. Таким образом, вероятность будет равна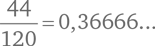 
В таблице вы можете видеть, как меняется вероятность по мере возрастания N.
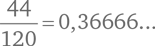В таблице вы можете видеть, как меняется вероятность по мере возрастания N.
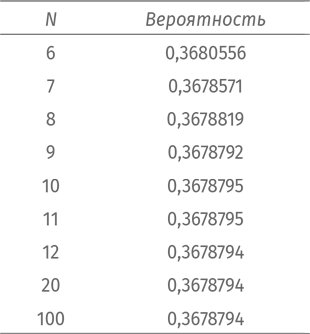
Вероятность меняется и дальше, но на ничтожно малую величину.
Хорошенько подумав, мы можем вывести формулу зависимости вероятности того, что никто из N зрителей не получит свою шляпу, от числа N:
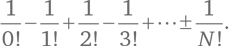
Например, при N = 4
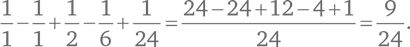
Это согласуется с нашими предыдущими выкладками.
В пределе, когда N стремится к бесконечности, вероятность того, что никто не получит свою шляпу, равна
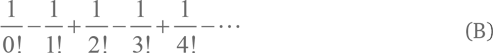
Этот ряд уходит в бесконечность. Обратите внимание, что эта формула похожа на формулу (A) для подсчета числа e. Сумма ряда (B) равна 
Мы снова встретили наше заветное число!
Мы снова встретили наше заветное число!Уже при N = 10 сумма ряда будет равна
Это достаточно близко к следующему значению:
Среднее расстояние между двумя простыми числами
В главе 1 я доказал, что простых чисел бесконечно много. Вы увидели, что среди небольших целых положительных чисел простые числа встречаются достаточно часто, но, когда мы уходим в бесконечность, простые числа начинают попадаться все реже. Мы можем с некоторой точностью установить, насколько редко встречаются простые числа, если попытаемся найти среднее расстояние между ними.
Какие простые числа можно найти между 1 и 20?
2, 3, 5, 7, 11, 13, 17, 19.
Промежутки (разности) между этими числами следующие:
1, 2, 2, 4, 2, 4, 2.
Следовательно, среднее расстояние между ними равно:
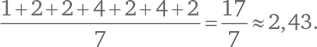
Теперь посчитаем, сколько простых чисел между 1 и 1000. Всего их 168: начиная с 2, 3 и 5 и заканчивая 983, 991 и 997. Среднее расстояние между соседними простыми числами в этом случае составит:
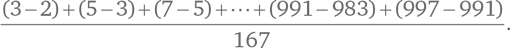
Знаменатель равен 167, так как простых чисел 168, а промежутков между ними на 1 меньше. Числитель можно посчитать довольно просто. Обратите внимание, что число 3 встречается дважды с разными знаками. Та же история с числом 5. Разумеется, это верно для всех чисел, кроме первого и последнего. Таким образом, нам достаточно вычесть 2 из 997. Получается, что среднее расстояние между простыми числами от 1 до 1000 равно
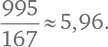
Это в два с лишним раза больше, чем в случае, когда мы брали числовой ряд от 1 до 20.
Введем обозначение agap(N) для среднего расстояния между простыми числами от 1 до N. Тогда наши предыдущие расчеты могут быть записаны в таком виде:
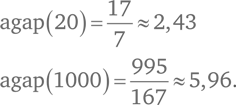
Вычислим среднее расстояние между простыми числами от 1 до N, когда N равно 100, 1000, 10 000 и так далее до 1 000 000 000. И округлим результат до тысячных:
Легко заметить: когда N становится больше в десять раз, agap(N) возрастает примерно на 2,3.
Мы можем проиллюстрировать эту закономерность на графике. Будем отмечать число N по оси абсцисс и agap(N) по оси ординат. Масштаб по оси ординат оставим обычным, а по оси абсцисс разница между делениями пусть постоянно возрастает в 10 раз (это называется логарифмическая шкала):
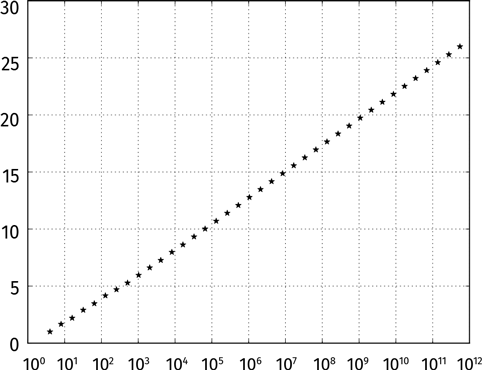
Обратите внимание: звездочки выстроились почти в прямую линию. Если присмотреться, левый нижний конец нашей кривой слегка загибается вверх.
Если бы звездочки на графике в точности выстроились в линию, мы получили бы следующую формулу, включающую число Эйлера:
N = ea + 1. (C)
Здесь а=agap(N) Скажем, если N = 1012, то agap(N) ≈ 26,59. Для выполнения (C) необходимо, чтобы a ≈ 26,63, и наш результат близок к этому числу.
Чудесная формула
Три главы были посвящены трем важным числам: π, i, e. Хотите верьте, хотите нет, но все они встречаются в одной формуле (которую вывел Эйлер):
eiπ + 1 = 0.
Формула поражает невероятным изяществом и простотой, однако как можно возводить число в мнимую степень?!
Мы знаем, как возвести e в целую положительную степень. Например, e³ = e × e × e. Отрицательная степень – это произведение дробей: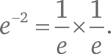 
Дробные степени могут быть выражены через квадратные корни, кубические корни и т. д.: 
Можно посчитать даже такую жутковатую величину, как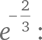 
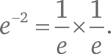Дробные степени могут быть выражены через квадратные корни, кубические корни и т. д.: Можно посчитать даже такую жутковатую величину, как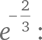
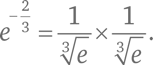
Но eiπ не вписывается в эти стандарты. Нам нужен иной принцип.
Мы знаем, что e представляет собой сумму бесконечного ряда:
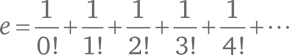
Для любого x значение ex будет:
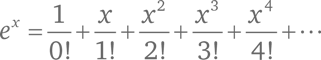
Скажем, в случае x = –1 мы получим знакомый по казусу со шляпами ряд (B):
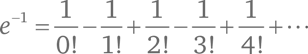
Чтобы узнать, чему равно eiπ, подставим iπ вместо x:
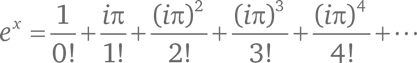
Чему равны числители дробей в этой сумме?
(iπ) ² = (iπ) × (iπ) = i² × π² = – π².(iπ) ³ = i × i × i × π³ = –1 × i × π³ = –iπ³.(iπ) ⁴ = i⁴ × π⁴ = π⁴.(iπ) ⁵ = –iπ⁵.(iπ) ⁶ = –π⁶.(iπ) ⁷ = –iπ⁷.(iπ) ⁸ = π⁸.
Элементы ряда поочередно оказываются то действительными, то мнимыми. Сгруппируем эти две категории элементов:
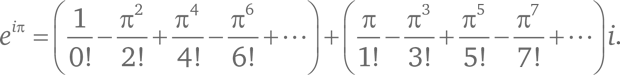
Оказывается, что выражение между первыми двумя скобками представляет собой в точности cos(π), то есть –1, а выражение между вторыми скобками равно sin(π), то есть 0. Таким образом,
eiπ = cos(π) + i sin(π) = –1 + 0i = –1.
Теперь мы понимаем, как возникла чудесная формула Эйлера.
