Итак, с помощью чудесного тонкого инструмента – рентгеновских лучей, благодаря которым, как помнят физики, тридцать лет назад была детально изучена атомная решетка кристаллов, биологи и физики, объединив усилия, опустили верхний предел размера микроскопических структур, отвечающих за определенные крупномасштабные признаки особи – «размер гена». Теперь перед нами встал серьезный вопрос: как с точки зрения статистической физики примирить те факты, что структура генов включает сравнительно небольшое число атомов (порядка 1000, а то и меньше), но тем не менее проявляет в высшей степени регулярную и упорядоченную активность, с постоянством и стабильностью, граничащими с чудом?

Позвольте мне еще раз подчеркнуть эту удивительную ситуацию. Несколько представителей династии Габсбургов обладают странной деформацией нижней губы – «габсбургской губой». Под покровительством императорского семейства Венская императорская академия тщательно изучила ее наследование и опубликовала результаты, вместе с историческими портретами. Судя по всему, этот признак является истинно менделевской «аллелью» по отношению к нормальной форме губы. Сосредоточившись на портретах члена семейства, жившего в XVI веке, и его потомка, жившего в XIX веке, можно смело предположить, что материальная структура гена, ответственная за эту аномальную черту, передавалась из поколения в поколение, воспроизводимая при каждом из не слишком многочисленных клеточных делений, разделяющих этих двух людей. Более того, число атомов, вовлеченных в соответствующую генную структуру, скорее всего, имеет тот же порядок, что и в случаях, изученных с помощью рентгеновского излучения. Все это время ген находился при температуре около 98 °F. Как объяснить, что за столетия разупорядочивающее тепловое движение не нарушило его целостности?

В конце прошлого века физик не смог бы ответить на данный вопрос, если бы опирался только на законы природы, которые был способен истолковать и действительно понимал. Поразмыслив о статистической ситуации, он бы сказал (как мы заметим, совершенно верно): этими материальными структурами могут быть только молекулы. К тому времени химия уже обладала обширными знаниями о существовании, а иногда и очень высокой стабильности таких атомных ассоциаций. Однако эти знания были чисто эмпирическими. Природа молекул оставалась загадкой – крепкая связь между атомами, поддерживающая форму молекулы, ставила всех в тупик. Да, это был бы верный ответ, однако его ценность была бы ограничена до тех пор, пока загадочная биологическая стабильность сводилась бы лишь к не менее загадочной химической стабильности. Свидетельство того, что два признака со схожим проявлением основаны на одном принципе, всегда шатко, если этот принцип неизвестен.

В данном случае объяснение дает квантовая теория. Согласно современным знаниям, механизм наследственности тесно связан – нет, основывается на самом базисе квантовой теории. Теорию эту открыл Макс Планк в 1900 году. Современную генетику можно датировать подтверждением де Фризом, Корренсом и Чермаком статьи Менделя (1900) и статьей де Фриза о мутациях (1903). Таким образом, две великие теории возникли почти одновременно, и неудивительно, что обеим следовало достичь определенной зрелости, прежде чем между ними проявится связь. Квантовой теории на это потребовалось более четверти века, пока в 1926 году В. Гайтлер и Ф. Лондон не разработали общие принципы квантовой теории химической связи. Теория Гайтлера – Лондона включает тонкие и сложные концепции последних достижений квантовой теории (квантовую механику, или волновую механику). Представить ее без вычислений практически невозможно или потребует отдельной небольшой книги. Но, к счастью, теперь, когда вся работа по прояснению нашего мышления проделана, можно прямо обозначить связь между квантовыми переходами и мутациями, выделить наиболее примечательную черту. Этим мы и займемся.

Величайшим откровением квантовой теории стало открытие дискретности в природе, в контексте, где, согласно сложившимся взглядам, что-либо кроме непрерывности выглядит абсурдным.

Первый подобный случай касался энергии. Крупное тело меняет энергию непрерывно. Например, раскачанный маятник постепенно замедляется благодаря сопротивлению воздуха. Странно, но следует признать, что система атомных масштабов ведет себя иначе. По причинам, в которые мы не можем здесь углубиться, нужно полагать, что маленькая система по природе своей обладает определенными дискретными величинами энергии, их называют свойственными ей энергетическими уровнями. Переход из одного состояния в другое представляет собой весьма загадочное событие, обычно называемое квантовым переходом.

Однако энергия – не единственная характеристика системы. Снова рассмотрим наш маятник, но такой, что осуществляет различные движения, – тяжелый шар, подвешенный на нитке к потолку. Он может качаться в направлении север – юг, или восток – запад, или любом ином, или описывать круг, или эллипс. Аккуратно обдувая шар мехами, можно заставить маятник непрерывно переключаться от одного вида движения к другому.

Для мелкомасштабных систем большинство этих или схожих характеристик – мы не станем вдаваться в детали – меняются дискретно. Они «квантованы», как энергия.

В результате атомные ядра с их электронными оболочками, оказываясь в непосредственной близости друг к другу и формируя систему, не могут принять любую произвольную конфигурацию. По своей природе они выбирают из многочисленного, но дискретного числа состояний. Обычно мы называем их уровнями, или энергетическими уровнями, поскольку энергия играет важную роль в данной характеристике. Но следует понимать, что полное описание включает не только энергию. По сути надо говорить о состоянии как об определенной конфигурации всех частиц.

Переход из одной конфигурации в другую является квантовым переходом. Если вторая конфигурация обладает большей энергией («более высокий уровень»), для перехода необходимо снабдить систему извне количеством энергии, хотя бы равным разнице между двумя уровнями. Переход на низший уровень может происходить самопроизвольно, а избыток энергии будет рассеян в виде излучения.

Среди дискретных состояний некой выборки атомов может существовать самый нижний уровень, соответствующий близкому расположению ядер относительно друг друга. В таком состоянии атомы формируют молекулу. Следует подчеркнуть, что молекула поневоле будет обладать определенной стабильностью. Ее конфигурация остается неизменной, если извне нет притока энергии, равной хотя бы разнице, необходимой для «подъема» на более высокий уровень. Таким образом, эта разница между уровнями, имеющая количественное выражение, количественно определяет степень стабильности молекулы. Мы увидим, как тесно данный факт связан с самими основами квантовой теории – с дискретностью энергетических уровней.

Я вынужден просить читателя принять на веру то, что этот набор идей полностью подтверждается химическими фактами – и успешно объясняет основополагающую концепцию химической валентности и многие детали молекулярной структуры, энергию связи, стабильность при различных температурах и т. п. Я говорю о теории Гайтлера – Лондона, которую, как я уже упоминал, невозможно рассмотреть здесь подробно.

Мы должны удовлетвориться рассмотрением вопроса, представляющего важность для нашего биологического исследования, а именно стабильности молекулы при различных температурах. Предположим, что наша система атомов вначале находится в состоянии с минимальной энергией. Физик назовет это молекулой при абсолютном нуле температуры. Чтобы перевести ее на следующий более высокий уровень, необходим приток определенного количества энергии. Простейший способ предоставить его – «нагреть» молекулу, перенести ее в окружающую среду с большей температурой (термостат), тем самым позволив другим системам (атомам, молекулам) сталкиваться с нашей молекулой. Поскольку тепловое движение хаотично, не существует температурного порога, при котором «подъем» произойдет обязательно и немедленно. Скорее при любой температуре, отличной от абсолютного нуля, существует бо́льшая или меньшая вероятность такого «подъема», и она, разумеется, растет с ростом температуры в термостате. Лучший способ выразить эту вероятность – указать среднее время, которое придется ждать перехода, – «время ожидания».

Из эксперимента, согласно М. Полани и Ю. Вигнеру, следует, что «время ожидания» преимущественно зависит от соотношения двух энергий: собственно энергетической разницы, необходимой для достижения желаемого эффекта, (обозначим ее W) и энергии, характеризующей интенсивность теплового движения при рассматриваемой температуре (обозначим абсолютную температуру T, а характеристическую энергию – kT). Очевидно, что чем выше переход в сравнении со средней тепловой энергией – то есть чем выше отношение W: kT, – тем меньше его вероятность и, соответственно, больше время ожидания. Удивительно, насколько сильно время ожидания зависит от сравнительно небольших изменений отношения W: kT. Приведу следующий пример (из Дельбрюка): если W в 30 раз больше kT, время ожидания составит 0,1 секунды, но вырастет до 16 месяцев при W в 50 раз больше kT – и до 30 000 лет при W в 60 раз больше kT!

Возможно, следует выразить математическим языком – для читателей, которым это нравится, – причину столь высокой чувствительности к изменениям энергетической разницы или температуры, а также добавить несколько физических комментариев по этому поводу. Причина заключается в том, что время ожидания – обозначим его t – экспоненциально зависит от отношения W/kT:

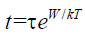
где τ – некая малая константа порядка 10^–13 или 10^–14 c. Данная экспоненциальная функция возникла не случайно. Она вновь и вновь появляется в статистической теории и, так сказать, составляет ее основу. Это мера невероятности того, что количество энергии, равное W, случайно соберется в некой части системы, и именно эта невероятность возрастает столь сильно, когда данное количество многократно превышает «среднюю энергию» kT.

На самом деле, W = 30 kT (см. пример выше) – уже редкий случай. То, что он не приводит к очень долгому времени ожидания (всего 0,1 секунды в нашем примере), разумеется, связано с малостью фактора τ. Этот фактор имеет физическое значение. Он примерно соответствует периоду колебаний, постоянно происходящих в системе. В широком смысле можно сказать, что, согласно этому фактору, вероятность накопления нужного количества W, пусть и небольшая, реализуется снова и снова «при каждом колебании», то есть 10¹³–10¹⁴ раз в секунду.

Приведя эти рассуждения в качестве теории стабильности молекулы, мы по умолчанию полагали, что квантовый переход («подъем») ведет если не к полному распаду, то по меньшей мере к значительному изменению конфигурации атомов – изомерной молекуле, как выразился бы химик, то есть молекуле, состоящей из тех же атомов, которые организованы другим образом (в биологии это будет другая «аллель» в том же «локусе», а квантовый скачок будет соответствовать мутации).

Чтобы использовать подобную интерпретацию, необходимо скорректировать два момента в нашей истории, которую я намеренно упростил для ясности. На основании моих слов можно решить, будто лишь в самом нижнем энергетическом состоянии группа атомов формирует то, что мы называем молекулой, а на следующей ступени превращается в «нечто иное». Это не так. В действительности за низшим уровнем следует плотная серия уровней, на которых не происходит значительных изменений конфигурации и которые соответствуют слабым колебаниям атомов, упомянутым выше. Уровни тоже «квантованы», но ступени между ними сравнительно малы. Поэтому удары частиц в «термостате» могут перевести молекулу на данные уровни при достаточно низких температурах. Если молекула представляет собой протяженную структуру, то можно считать эти колебания высокочастотными звуковыми волнами, пробегающими по молекуле, но не причиняющими ей вреда.

Итак, первая поправка не слишком серьезна: мы должны пренебречь «тонкой колебательной структурой» диаграммы энергетических уровней. Под «следующим более высоким уровнем» следует понимать уровень, соответствующий значительному изменению конфигурации.

Объяснить вторую поправку намного труднее, поскольку она связана с жизненно важными, но весьма сложными особенностями диаграммы значимо различающихся уровней. Свободный переход между уровнями может быть затруднен, вне зависимости от требуемого количества энергии; на самом деле, может быть затруднен даже переход с верхнего уровня на нижний.

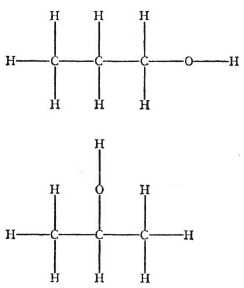
Рис. 11. Два изомера пропилового спирта

Начнем с эмпирических фактов. Химик знает, что одна и та же группа атомов может объединяться различными способами, формируя молекулы. Такие молекулы называют изомерами («состоящими из одинаковых частей»; ἴσος – одинаковый, μέρος – часть). Изомерия – правило, а не исключение. Чем крупнее молекула, тем больше изомеров может существовать. На рис. 11 показан один из простейших случаев, два вида пропилового спирта, каждый включает 3 атома углерода (С), 8 атомов водорода (H) и один атом кислорода (O). Последний может стоять между любым водородом и углеродом, однако лишь два случая на рисунке являются различными веществами. Так оно и есть. Все их химические и физические константы заметно различаются. Кроме того, различаются их энергии – они представляют собой «различные уровни».

Примечательным является факт, что обе молекулы стабильны и ведут себя так, словно являются «низшими состояниями». Не происходит спонтанного перехода из одного состояния в другое.

Причина заключается в том, что эти две конфигурации не соседствующие. Переход из одной в другую может осуществиться лишь через промежуточные конфигурации, обладающие большей энергией. Грубо говоря, кислород нужно извлечь из одного положения и перенести в другое. Судя по всему, не существует способа сделать это, минуя конфигурации со значительно большей энергией. Положение дел иногда образно изображают так, как представлено на рис. 12, где 1 и 2 соответствуют двум изомерам, 3 – «порогу» между ними, а две стрелки показывают «подъем», то есть количество энергии, необходимое для перехода из состояния 1 в состояние 2 или из состояния 2 в состояние 1 соответственно.

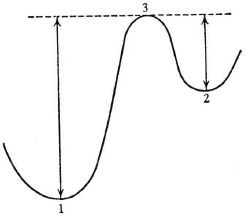
Рис. 12. Энергетический порог (3) между изомерными уровнями (1) и (2). Стрелками показаны минимальные энергии, необходимые для перехода

Теперь мы можем внести «вторую поправку», она заключается в том, что переходы подобного «изомерного» рода – единственное, что интересует нас в приложении к биологии. Именно их мы имели в виду, рассматривая «стабильность». Под «квантовым переходом» мы подразумеваем переход из одной относительно стабильной молекулярной конфигурации в другую. Количество энергии, необходимое для перехода (W), есть не реальная разница между уровнями, а шаг с исходного уровня на пороговый (см. стрелки на рис. 12).

Переходы без порога между исходным и конечным состоянием нас совершенно не интересуют – и не только в биологическом смысле. Они ничего не привносят в химическую стабильность молекулы. Почему? У них нет длительного эффекта, они остаются незамеченными. Когда они происходят, мгновенно следует возврат в исходное состояние, которому ничто не препятствует.