Из данных фактов вытекает простой ответ на наш вопрос: могут ли эти структуры, построенные из относительно небольшого числа атомов, длительное время противостоять тепловому движению, которому непрерывно подвергается наследственный материал? Предположим, что ген представляет собой огромную молекулу, способную лишь на дискретные изменения, заключающиеся в перестановке атомов и появлении изомерных молекул. Для удобства я и дальше буду называть этот переход изомерным, хотя нелепо исключать возможность обмена с окружающей средой. Перестановка может затронуть небольшой участок гена, и вероятно множество различных перестановок. Энергетические пороги, отделяющие существующую конфигурацию от любой изомерной, должны быть достаточно высоки в сравнении со средней тепловой энергией атома, чтобы такой обмен являлся редким событием. Подобные редкие события мы назовем спонтанными мутациями.

Остаток главы будет посвящен проверке этого общего взгляда на ген и мутацию, которым мы обязаны в основном немецкому физику Дельбрюку, путем подробного сравнения с генетическими фактами. Но прежде сделаем несколько уместных комментариев об основании и общей природе теории.

Необходимо ли при рассмотрении биологического вопроса копать столь глубоко и основывать взгляд на квантовой механике? Сейчас предположение о том, что гены являются молекулами, широко распространено. Найдется мало биологов – знакомых с квантовой теорией или нет, – кто не согласится с ним. Ранее мы позволили доквантовому физику озвучить его как единственное разумное объяснение наблюдаемой стабильности. Последующие рассуждения об изомерии, пороговой энергии, важной роли отношения W: kT в определении вероятности изомерного перехода можно было бы представить с чисто эмпирической позиции, уж точно не обращаясь к квантовой теории. Почему же я так настаивал на квантово-механической точке зрения, хотя и не могу доступно объяснить ее в этой книге и рискую утомить читателей?

Квантовая механика – первая теоретическая точка зрения, основные принципы которой позволяют учесть все виды скоплений атомов, встречающиеся в природе. Зависимость Гайтлера – Лондона – уникальная, исключительная особенность данной теории, придуманная не для объяснения химической связи. Она возникает сама по себе, весьма интересным и загадочным образом, на основании различных рассуждений. Полностью согласуется с наблюдаемыми химическими фактами, и, как я уже говорил, это уникальная особенность, достаточно понятная, чтобы сказать с определенной уверенностью: в квантовой теории «такого больше не произойдет».

Соответственно, мы можем смело утверждать, что у молекулярного объяснения наследственного материала нет альтернативы. Физическая точка зрения не позволяет иным образом объяснить его стабильность. Если взгляд Дельбрюка не подтвердится, то мы будем вынуждены сдаться. Это первое мое заявление.

Однако вы можете спросить: неужели молекулы – единственные стабильные структуры из атомов? А как насчет, например, золотой монеты, две тысячи лет пролежавшей в гробнице и сохранившей отчеканенный на ней портрет? Конечно, монета состоит из множества атомов, но в данном случае мы не склонны объяснять сохранение формы статистикой простых чисел. То же самое касается выросших в скале аккуратных кристаллов, остающихся неизменными на протяжении геологических эпох.

Это подводит нас ко второму вопросу, который я хочу прояснить. Случаи молекулы, твердого вещества и кристалла не так уж различаются. В свете современных знаний они почти одинаковы. К сожалению, школьное образование придерживается определенных традиционных взглядов, а они давно устарели и затрудняют понимание действительного положения вещей.

Информация о молекулах, которую мы получаем в школе, не дает ни малейшего приставления о том, что они ближе к твердому состоянию, нежели к жидкому или газообразному. Напротив, нас учат различать физические превращения, такие как плавление или испарение, при которых молекулы сохраняются (например, этиловый спирт в твердом, жидком и газообразном состоянии всегда состоит из одних и тех же молекул, C₂H₆O), и химические, такие как горение спирта:

C₂H₆O + 3O₂ = 2CO₂ + 3H₂O,

при котором молекула спирта и три молекулы кислорода претерпевают перестановку и превращаются в две молекулы углекислого газа и три молекулы воды.

Про кристаллы нам говорят, что они формируют тройные периодические решетки, в них иногда можно узнать структуру отдельной молекулы, как в случае спирта и большинства органических веществ, в то время как в других кристаллах, например каменной соли (NaCl), нельзя четко выделить молекулы NaCl, поскольку каждый атом Na симметрично окружен шестью атомами Cl, и наоборот, а потому пары молекулярных партнеров обозначаются весьма условно.

Наконец, нас учат, что твердое вещество бывает кристаллическим или нет – в последнем случае его называют аморфным.

Я не стану заявлять, будто все эти утверждения и разграничения ошибочны. Иногда весьма полезны для практических целей. Однако при истинном рассмотрении структуры материи пределы следует обозначать иначе. Фундаментальное различие лежит между двумя строками данной схемы «уравнений»:

молекула = твердое вещество = кристалл

газ = жидкость = аморфное вещество

Вкратце объясним эти утверждения. Так называемые аморфные твердые вещества в действительности не являются ни аморфными, ни твердыми. Рентгеновский анализ выявил рудиментарную структуру кристалла графита в «аморфном» угольном волокне. Итак, уголь представляет собой твердое и одновременно кристаллическое вещество. Если кристаллической структуры не выявлено, то материал следует считать жидкостью с очень высокой «вязкостью» (внутренним трением). Отсутствие четко определенной температуры плавления и скрытой теплоты плавления свидетельствует о том, что такое вещество не является истинно твердым. При нагревании оно постепенно размягчается и в конце концов становится жидким. Помню, в конце Первой мировой войны нам в Вене выдавали похожую на асфальт субстанцию в качестве заменителя кофе. Она была такой твердой, что приходилось использовать стамеску или топорик, чтобы разломать маленький кирпичик на гладкие кусочки. Однако со временем субстанция начинала вести себя как жидкость, уплотняясь в нижней части сосуда, где вы имели неосторожность оставить ее на пару дней.

Непрерывность газовой и жидкой фазы хорошо известна. Можно постепенно сжижать газ, минуя так называемую критическую точку. Но здесь мы не будем этого касаться.

Мы только что разъяснили в представленной выше схеме все, кроме самого главного, а именно нашего желания считать молекулу твердым = кристаллическим веществом.

Причина заключается в том, что формирующие молекулу атомы – вне зависимости от их количества – связывают силы той же природы, что и многочисленные атомы, составляющие истинно твердое вещество, кристалл. Молекула демонстрирует стойкость структуры, схожую с кристаллической. Помните, что этой же стойкостью мы объясняем стабильность гена!

Важное различие в структуре вещества определяется тем, связаны ли атомы этими «укрепляющими» силами Гайтлера – Лондона или нет. В твердом веществе и в молекуле – да. В состоящем из отдельных атомов газе, например парах ртути, – нет. В газе, состоящем из молекул, только атомы в каждой молекуле соединены подобным образом.

Маленькую молекулу можно считать зародышем твердого вещества. Существует два способа строить на основе этого маленького твердого зародыша более крупные ассоциации. Первый весьма скучен: снова и снова повторять одну и ту же структуру в трех направлениях. Так происходит в растущем кристалле. После установления периодичности не существует определенного предела размеров агрегата. Второй способ – собирать более крупный агрегат, не прибегая к утомительному повторению. Это касается сложных органических молекул, в которых каждый атом и группа атомов играют определенную роль, не полностью эквивалентную ролям других атомов, как наблюдается в периодической структуре. Мы можем назвать данный случай апериодическим кристаллом или твердым веществом и выразить нашу гипотезу следующим образом: мы считаем, что ген – а может, и вся хромосомная фибрилла – представляет собой апериодическое твердое вещество.

Часто задают вопрос: как крупинка вещества – ядро оплодотворенной яйцеклетки – вмещает сложный код, определяющий будущее развитие организма? Упорядоченное скопление атомов, обладающее необходимой стабильностью для поддержания своей упорядоченности, выглядит единственной подходящей материальной структурой, подразумевающей возможность достаточного количества различных («изомерных») перестроек для установления сложной системы «определителей» в небольших пространственных рамках. Действительно, не слишком много атомов в такой структуре хватит для почти бесконечного числа возможных перестановок. Сравним это с азбукой Морзе. Два различных символа – точка и тире – в упорядоченных группах, имеющих не более четырех символов, позволяют получить тридцать различных обозначений. Если добавить к точке и тире третий символ и использовать группы, содержащие не более десяти символов, можно будет обозначить 88 572 различные «буквы». Увеличив число символов до пяти, а длину групп – до двадцати пяти, мы получим 372 529 029 846 191 405 «букв».

Мне возразят, что это сравнение ошибочно, поскольку символы азбуки Морзе могут иметь различный состав (например, ⋅– и ⋅⋅—), а значит, являются плохим примером изомерии. Чтобы исправить этот недостаток, давайте выберем из третьего примера только комбинации, содержащие ровно 25 символов и ровно по 5 символов каждого вида (5 точек, 5 тире и т. д.). Согласно приблизительным подсчетам, число сочетаний составит 62 330 000 000 000, где нули справа заменяют цифры, которые я не стал вычислять.

Разумеется, в реальности отнюдь не «каждая» организация группы атомов будет представлять собой возможную молекулу. Кроме того, код нельзя выбрать произвольным образом, ведь он сам должен быть действующим фактором, вызывающим развитие. С другой стороны, число, взятое нами для примера (25), очень мало, и мы допустили только простые перестановки в линейной последовательности. Я хочу проиллюстрировать факт, что молекулярные представления о гене позволяют предположить возможность того, что миниатюрный код полностью соответствует сложному и конкретному плану развития и содержит способы его реализации.

Давайте наконец сравним теоретическую картину с биологическими фактами. Очевидно, первый вопрос состоит в том, способна ли она объяснить наблюдаемую высокую стабильность. Являются ли пороговые значения, равные многократной средней тепловой энергии kT, разумными, лежат ли в пределах, даваемых обычной химией? Это тривиальный вопрос, на него можно ответить утвердительно, не прибегая к таблицам. Молекулы любого вещества, которое химик выделяет при некой температуре, должны при этой температуре обладать временем жизни не короче нескольких минут. (Мягко говоря; как правило, намного длиннее.) Таким образом, пороговые значения, с какими сталкивается химик, соответствуют порядку величин, объясняющих любой уровень стабильности, с которым может встретиться биолог. Пороговые значения, соотносящиеся друг с другом как 1:2, будут соответствовать временам жизни от доли секунды до десятков тысяч лет.

Но давайте приведем числа, которые нам еще пригодятся. Отношения W/kT, данные для примера на стр. 51, а именно:

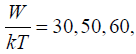
дающие время жизни

0,1 с, 16 месяцев, 30 000 лет,

соответственно, при комнатной температуре будут соответствовать пороговым значениям, равным

0,9, 1,5, 1,8 электронвольт.

Нужно объяснить единицу электронвольт, которая весьма удобна для физиков, поскольку ее можно представить наглядно. Например, третье число (1,8) означает, что электрон, ускоренный напряжением около 2 вольт, приобретет достаточную энергию, чтобы при ударе вызвать переход. Для сравнения: батарейка обычного карманного фонарика дает напряжение около 3 вольт.

Эти рассуждения позволяют предположить, что изомерное изменение конфигурации в некой части нашей молекулы, вызванное случайной флуктуацией колебательной энергии, действительно может являться достаточно редким событием, чтобы интерпретировать его как спонтанную мутацию. Таким образом, используя принципы квантовой механики, мы объясняем удивительнейшую особенность мутаций, которая и привлекла внимание де Фриза, а именно их «скачкообразные» вариации без промежуточных форм.

Обнаружив повышение частоты природных мутаций под воздействием любого ионизирующего излучения, можно решить, будто естественная частота мутаций зависит от радиоактивности почвы и воздуха, а также космического излучения. Однако количественное сравнение с результатами рентгеновского исследования показывает, что «природная радиация» намного слабее и объясняет лишь небольшую часть естественных мутаций.

Учитывая, что нам приходится доказывать редкость природных мутаций случайными флуктуациями теплового движения, не следует удивляться тому, что природа столь хитроумно выбрала пороговые значения, сделав мутацию редким событием. Ранее в лекциях мы пришли к выводу, что частые мутации вредят эволюции. Особи, по причине мутации приобретшие недостаточно стабильную генетическую конфигурацию, вряд ли могут надеяться на выживание своего «ультрарадикального», быстро мутирующего потомства. Вид избавится от них, а значит, приобретет стабильные гены путем естественного отбора

Разумеется, не следует ожидать, что все мутанты, которые появляются в наших экспериментах по скрещиванию и которых мы отбираем для изучения их потомства, будут проявлять эту высокую стабильность. Ведь они еще не подверглись «испытанию» – а если и подверглись, были «отклонены» диким типом, возможно, из-за слишком высокой неустойчивости. В любом случае нас не удивит факт, что в действительности часть этих мутантов намного менее стабильна, нежели нормальные гены дикого типа.

Благодаря этому мы можем проверить нашу формулу мутабельности:

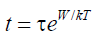
Не забудьте, что t – время ожидания возникновения мутации с энергетическим порогом W. Вопрос: как t меняется с температурой? Из вышеприведенной формулы нетрудно с хорошим приближением рассчитать отношение значений t при температурах T + 10 и T:

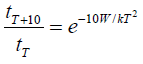
Поскольку экспонента отрицательна, это отношение меньше 1. Время ожидания снижается при повышении температуры, а мутабельность растет. Это можно проверить, и такую проверку провели на плодовой мушке дрозофиле, в диапазоне переносимых ею температур. На первый взгляд результаты оказались неожиданными. Низкая мутабельность генов дикого типа отчетливо выросла, однако сравнительно высокая мутабельность уже мутантных генов осталось прежней или выросла незначительно. Именно это и следует из сравнения двух формул. Высокое значение W/kT, необходимое, согласно первой формуле, для достижения больших t (стабильные гены), приведет к низкому значению соотношения из второй формулы, то есть значительному повышению мутабельности с температурой. Обратная величина, 2–5, приблизительно соответствует температурному коэффициенту в эмпирическом правиле Вант-Гоффа для обычных химических реакций.

Теперь обратимся к частоте мутаций, индуцированных рентгеновским излучением. Из экспериментов по скрещиванию мы уже знаем, что, во-первых, согласно пропорциональности частоты мутаций дозе облучения, некое отдельное событие вызывает мутацию. Во-вторых, на основании количественных результатов и факта, что частота мутаций определяется интегральной плотностью ионизации и не зависит от длины волны, это отдельное событие должно представлять собой ионизацию или сходный процесс, происходящий в определенном объеме порядка 10 атомных расстояний в кубе, чтобы дать соответствующую мутацию. Согласно нашим взглядам, энергия для преодоления порога должна возникнуть благодаря этому взрывообразному процессу, ионизации или излучению. Я называю его взрывообразным, поскольку энергия, затраченная на один акт ионизации (кстати, это энергия не самого рентгеновского излучения, а созданного ею вторичного электрона), хорошо известна – это сравнительно большое значение, 30 электронвольт. Она должна значительно активировать тепловое движение в точке своего выделения и распространиться из нее тепловой волной – волной интенсивных колебаний атомов. Вероятно, тепловая волна способна обеспечить нужную пороговую энергию в 1–2 электронвольта при среднем «радиусе действия» около 10 атомных расстояний, хотя беспристрастный физик ожидал бы чуть меньшего радиуса действия. Можно полагать, что во многих случаях результатом такого взрыва станет не упорядоченный изомерный переход, а повреждение хромосомы, которое окажется фатальным, если путем изобретательного скрещивания убрать неповрежденного партнера – соответствующую хромосому из второго набора – и заменить ее партнером, также несущим повреждение в соответствующем гене. Именно это и наблюдается.

Эта картина позволяет если не предсказать другие особенности, то хотя бы легко их объяснить. Например, нестабильный мутант в среднем не проявляет более высокой частоты рентгеновских мутаций по сравнению со стабильным. Если при взрыве выделяется количество энергии, равное 30 электронвольтам, не следует ожидать, будто незначительные различия в энергетических порогах – скажем, 1 и 1,3 вольта – будут иметь существенное значение.

В некоторых случаях переход изучили в обоих направлениях, то есть от некоего «дикого» гена к определенному мутанту и обратно, от мутанта к гену дикого типа. В такой ситуации естественная частота мутаций иногда близка, а иногда сильно различается. На первый взгляд это озадачивает, поскольку в обоих случаях вроде бы необходимо преодолеть один и тот же порог. Но, разумеется, это не всегда так, ведь отправной точкой является энергетический уровень начальной конфигурации, а он может быть различным для мутантного гена и гена дикого типа (см. рис. 12 на стр. 54, где «1» может означать аллель дикого типа, а «2» – мутантную аллель, более низкой стабильности которой соответствует более короткая стрелка).

В целом, я полагаю, «модель» Дельбрюка весьма неплохо выдерживает проверки, и мы можем использовать ее для дальнейших рассуждений.