Глава 3. Стратегия

Если видишь хороший ход — ищи ход получше.

Эмануэль Ласкер

В историю входят те полководцы, что достигали выдающихся результатов с помощью надежной стратегии. Чтобы успешно решать задачи, необходимо быть хорошим стратегом. Эта глава посвящена основным стратегиям, использующимся при проектировании алгоритмов. Вы узнаете:

как справляться с повторяющимися задачами посредством итераций;

как изящно выполнять итерации при помощи рекурсии;

как использовать полный перебор;

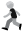как выполнять проверку неподходящих вариантов и возвращаться на шаг назад;

как экономить время при помощи эвристических алгоритмов, помогающих найти разумный выход;

как применять принцип «Разделяй и властвуй» к самым неподатливыми противникам;

как динамически идентифицировать уже решенные задачи, чтобы снова не тратить на них энергию;

как ограничивать рамки задачи.

Вам предстоит познакомиться с множеством инструментов, но не переживайте — мы начнем с простых задач, а затем по мере изучения новых методов постепенно будем находить все лучшие решения. Достаточно скоро вы научитесь просто и изящно справляться с вычислительными задачами.

3.1. Итерация

Итеративная стратегия состоит в использовании циклов (например, for и while) для повторения процесса до тех пор, пока не окажется соблюдено некое условие. Каждый шаг в цикле называется итерацией. Итерации очень полезны для пошагового просмотра входных данных и применения одних и тех же операций к каждой их порции. Вот пример.

Объединение списков рыб У вас есть списки морских и пресноводных рыб, оба упорядочены в алфавитном порядке. Как создать из них один общий список, тоже отсортированный по алфавиту?

Мы можем сравнивать в цикле верхние элементы двух списков (рис. 3.1).

Данный процесс можно записать в виде одного цикла с условием продолжения while loop:

function merge(sea, fresh)

    result ← List.new

 

    while not (sea.empty and fresh.empty)

        if sea.top_item > fresh.top_item

            fish ← sea.remove_top_item

       else

           fish ← fresh.remove_top_item

     result.append(fish)

 

return result

 

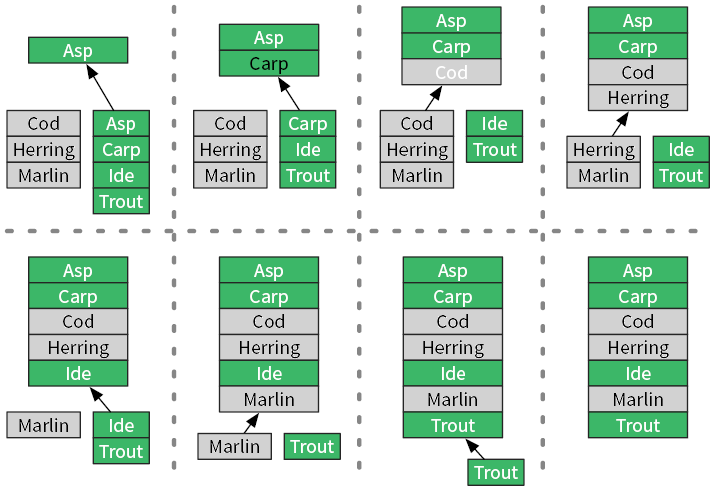
Рис. 3.1. Объединение двух отсортированных списков в третий, тоже отсортированный

Он выполняет обход всех названий рыб из входных списков, совершая фиксированное число операций для каждого элемента. Следовательно, алгоритм слияния merge имеет сложность O(n).

Вложенные циклы и степенные множества

В предыдущей главе мы увидели, как функция сортировки выбором selection_sort использует один цикл, вложенный в другой. Сейчас мы научимся использовать вложенный цикл для вычисления степенного множества. Если дана коллекция объектов S, то степенное множество S есть множество, содержащее все подмножества S.

Исследование запахов В парфюмерии цветочные ароматы изготавливают путем комбинирования запахов различных цветов. Если дано множество цветов F, то как посчитать все ароматы, которые можно изготовить из них?

Любой аромат состоит из подмножества F, потому его степенное множество содержит все возможные ароматы. Это степенное множество вычисляется итеративно. Для нулевого множества цветов есть всего один вариант — без запаха. В случае, когда мы берем очередной цветок, мы дублируем уже имеющиеся ароматы и добавляем его к ним (рис. 3.2).

Этот процесс можно описать при помощи циклов. Во внешнем цикле мы принимаем решение, какой цветок будем рассматривать следующим. Внутренний цикл дублирует ароматы и добавляет новый цветок к этим копиям.

function power_set(flowers)

    fragrances ← Set.new

    fragrances.add(Set.new)

    for each flower in flowers

        new_fragrances ← copy(fragrances)

        for each fragrance in new_fragrances

            fragrance.add(flower)

        fragrances ← fragrances + new_fragrances

    return fragrances

Добавление каждого нового цветка приводит к удвоению количества ароматов в множестве fragrances, что говорит об экспоненциальном росте (2k+1 = 2 × 2k). Алгоритмы, которые удваивают число операций, если объем входных данных увеличивается на один элемент, — экспоненциальные, их временная сложность — O(2n).

Генерирование степенных множеств эквивалентно генерированию таблиц истинности (см. раздел «Логика» в главе 1). Если обозначить каждый цветок логической переменной, то любой аромат легко представить в виде значений True/False этих переменных. В таблице истинности каждая строка будет возможной формулой аромата.

 

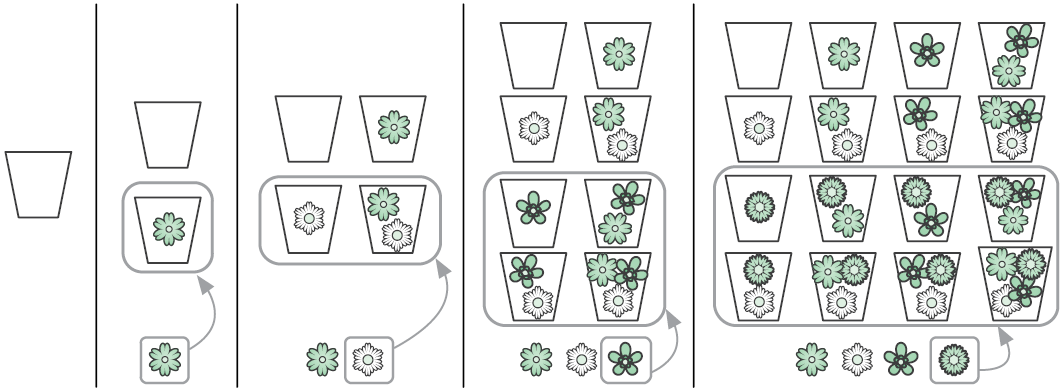
Рис. 3.2. Итеративное перечисление всех ароматов с использованием четырех цветков

3.2. Рекурсия

Мы говорим о рекурсии, когда функция делегирует работу своим клонам. Рекурсивный алгоритм естественным образом приходит на ум, когда нужно решить задачу, сформулированную с точки зрения самой себя. Например, возьмем известную последовательность Фибоначчи. Она начинается с двух единиц, и каждое последующее число является суммой двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21. Как создать функцию, возвращающую n-е число Фибоначчи (рис. 3.3)?

 

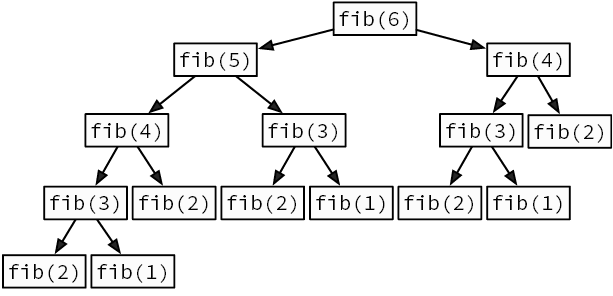
Рис. 3.3. Рекурсивное вычисление шестого числа Фибоначчи

function fib(n)

    if n ≤ 2

        return 1

    return fib(n - 1) + fib(n - 2)

При использовании рекурсии требуется творческий подход, чтобы понять, каким образом задача может быть поставлена с точки зрения самой себя. Чтобы проверить, является ли слово палиндромом, нужно посмотреть, изменится ли оно, если его перевернуть. Это можно сделать, проверив, одинаковы ли первая и последняя буквы слова и не является ли палиндромом заключенная между ними часть слова (рис. 3.4).

 

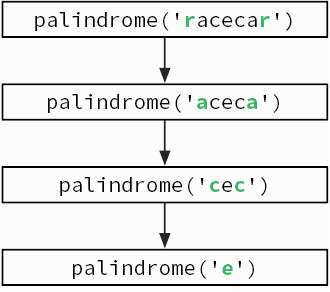
Рис. 3.4. Рекурсивная проверка, является ли слово racecar палиндромом

function palindrome(word)

    if word.length ≤ 1

        return True

    if word.first_char ≠ word.last_char

        return False

    w ← word.remove_first_and_last_chars

    return palindrome(w)

Рекурсивные алгоритмы имеют базовые случаи, когда объем входных данных слишком мал, чтобы его можно было продолжать сокращать. Базовые случаи для функции fib — числа 1 и 2; для функции palindrome это слова, состоящие из единственной буквы или не имеющие ни одной буквы.

Рекурсия против итераций

Рекурсивные алгоритмы обычно проще и короче итеративных. Сравните эту рекурсивную функцию с power_set из предыдущего раздела, которая не использует рекурсию:

function recursive_power_set(items)

    ps ← copy(items)

    for each e in items

       ps ← ps.remove(e)

       ps ← ps + recursive_power_set(ps)

       ps ← ps.add(e)

    return ps

Эта простота имеет свою цену. Рекурсивные алгоритмы при выполнении порождают многочисленные копии самих себя, создавая дополнительные вычислительные издержки. Компьютер должен отслеживать незаконченные рекурсивные вызовы и их частичные вычисления, что требует большего объема памяти. При этом дополнительные такты центрального процессора расходуются на переключение с одного рекурсивного вызова на следующий и назад.

Эту проблему можно наглядно увидеть на деревьях рекурсивных вызовов — диаграммах, показывающих, каким образом алгоритм порождает новые вызовы, углубляясь в вычисления. Мы уже видели деревья рекурсивных вызовов для поиска чисел Фибоначчи (см. рис. 3.3) и для проверки слов-перевертышей (см. рис. 3.4).

Если требуется максимальная производительность, то можно избежать этих дополнительных издержек, переписав рекурсивный алгоритм в чисто итеративной форме. Такая возможность есть всегда. Это компромисс: итеративный программный код обычно выполняется быстрее, но вместе с тем он более громоздкий и его труднее понять.

3.3. Полный перебор

Полный перебор, он же метод «грубой силы», предполагает перебор всех случаев, которые могут быть решением задачи. Эта стратегия также называется исчерпывающим поиском. Она обычно прямолинейна и незамысловата: даже в том случае, когда вариантов миллиарды, она все равно опирается исключительно на силу, то есть на способность компьютера проверить их все.

 

Рис. 3.5. Простое объяснение: полный перебор

Давайте посмотрим, как ее можно использовать, чтобы решить следующую задачу.

Лучшая сделка   У вас есть список цен на золото по дням за какой-то интервал времени. В этом интервале вы хотите найти такие два дня, чтобы, купив золото, а затем продав его, вы получили бы максимально возможную прибыль.

Не всегда у вас получится сделать покупку по самой низкой цене, а продать по самой высокой: первая может случиться позже второй, а перемещаться во времени вы не умеете. Алгоритм полного перебора позволяет просмотреть все пары дней. По каждой паре он находит прибыль и сравнивает ее с наибольшей, найденной к этому моменту. Мы знаем, что число пар дней в интервале растет квадратично по мере его увеличения. Еще не приступив к написанию кода, мы уже уверены, что он будет иметь O(n2).

Задача о лучшей сделке решается и с помощью других стратегий с меньшей временной сложностью — мы вскоре их рассмотрим. Но в некоторых случаях наилучшую временную сложность дает подход на основе полного перебора. Это имеет место в следующей задаче.

Рюкзак У вас есть рюкзак, вы носите в нем предметы, которыми торгуете. Его вместимость ограничена определенным весом, так что вы не можете сложить в него весь свой товар. Вы должны выбрать, что взять. Цена и вес каждого предмета известны, вам нужно посчитать, какое их сочетание дает самый высокий доход.

Степенное множество ваших предметов содержит все возможные их сочетания. Алгоритм полного перебора просто проверяет эти варианты. Поскольку вы уже знаете, как вычислять степенные множества, алгоритм не должен вызвать у вас затруднений:

function knapsack(items, max_weight)

    best_value ← 0

    for each candidate in power_set(items)

        if total_weight(candidate) ≤ max_weight

            if sales_value(candidate) > best_value

                best_value ← sales_value(candidate)

                best_candidate ← candidate

    return best_candidate

Для n предметов существует 2n подборок. В случае каждой из них мы проверяем, не превышает ли ее общий вес вместимости рюкзака и не оказывается ли общая стоимость подборки выше, чем у лучшей, найденной к этому времени. Иными словами, для каждой подборки выполняется постоянное число операций, а значит, алгоритм имеет сложность O(2n).

Однако проверять следует не каждую подборку предметов. Многие из них оставляют рюкзак полупустым, а это указывает на то, что существуют более удачные варианты. Далее мы узнаем стратегии, которые помогут оптимизировать поиск решения, эффективным образом отбраковывая неподходящие варианты.

3.4. Поиск (перебор) с возвратом

 

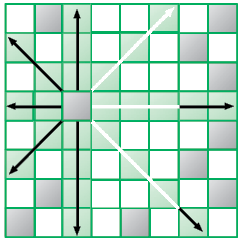
Вы играете в шахматы? Фигуры перемещаются на доске  8 × 8 клеток и поражают фигуры соперника. Ферзь — это самая сильная фигура: она поражает клетки по горизонтали, по вертикали и по двум диагоналям. Следующая стратегия будет объяснена в контексте известной шахматной задачи.

Задача о восьми ферзях Как разместить восемь ферзей на доске так, чтобы ни один из них не оказался под ударом других?

Попробуйте найти решение вручную, и вы увидите, что оно далеко не тривиальное. Рис. 3.6 показывает один из способов расположения мирно сосуществующих ферзей.

В разделе 1.3 мы видели, что восемь ферзей можно разместить на шахматной доске более чем 4 млрд способами. Решение искать ответ полным перебором, проверяя все варианты, я бы назвал неосмотрительным. Предположим, что первые два ферзя помещены на доску таким образом, что представляют угрозу друг для друга. Тогда независимо от того, где окажутся следующие ферзи, решение найти не удастся. Подход на основе полного перебора не учитывает этого и будет впустую тратить время, пытаясь разместить всех обреченных ферзей.

 

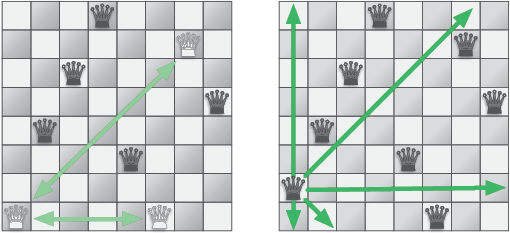
Рис. 3.6. Крайний левый ферзь может бить двух других. Если переместить его на одну клетку вверх, то он не будет никому угрожать

Более эффективный поход состоит в поиске только приемлемых позиций для фигур. Первого ферзя можно поместить куда угодно. Приемлемые позиции для каждого следующего будут ограничены уже размещенными фигурами: нельзя ставить ферзя на клетку, находящуюся под ударом другого ферзя. Если мы начнем руководствоваться этим правилом, мы, вероятно, получим доску, где невозможно разместить дополнительного ферзя, еще до того, как число фигур дойдет до восьми (рис. 3.7).

Это будет означать, что последнего ферзя мы разместили неправильно. Потому нам придется отойти назад — вернуться к предыдущей позиции и продолжить поиск. В этом заключается суть стратегии поиска с возвратом: продолжать размещать ферзей в допустимые позиции. Как только мы окажемся в тупике, мы отойдем назад, к моменту, предшествовавшему размещению последнего ферзя. Этот процесс можно оптимизировать при помощи рекурсии:

function queens(board)

    if board.has_8_queens

        return board

    for each position in board.unattacked_positions

        board.place_queen(position)

        solution ← queens(board)

        if solution

            return solution

        board.remove_queen(position)

    return False

 

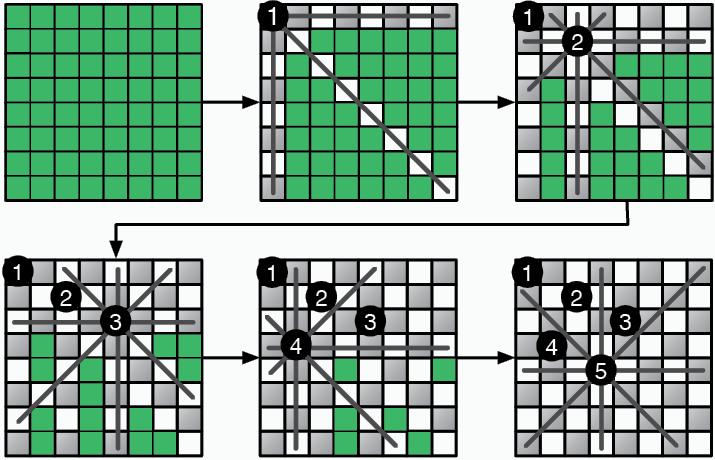
Рис. 3.7. Размещение ферзей ограничивает число приемлемых клеток для следующих фигур

Если требуемое по условию сочетание позиций на доске еще не найдено, функция обходит все приемлемые позиции для следующего ферзя. Она использует рекурсию, чтобы проверить, даст ли размещение ферзя в каждой из этих позиций решение. Как работает процесс, показано на рис. 3.8.

Поиск с возвратом лучше всего подходит для задач, где решением является последовательность вариантов, и выбор одного из них ограничивает выбор последующих. Этот подход позволяет выявлять варианты, которые не дают желаемого решения, так что вы можете отступить и попробовать что-то еще. Ошибитесь как можно раньше, чтобы двигаться дальше.

 

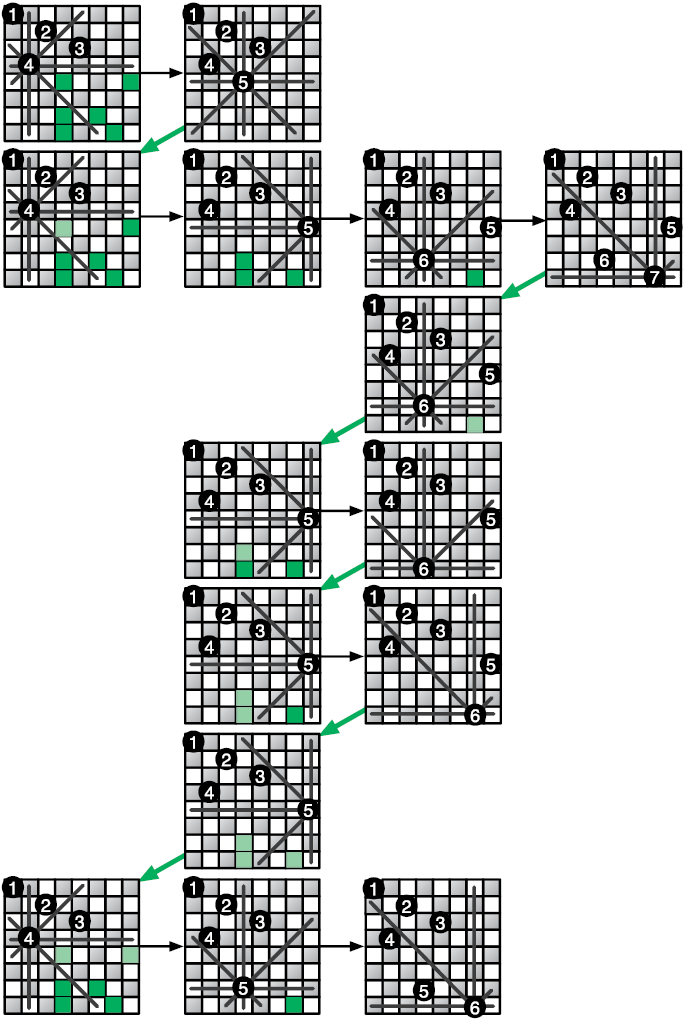
Рис. 3.8. Поиск с возвратом в «Задаче о восьми ферзях»

3.5. Эвристические алгоритмы

В обычных шахматах — 32 фигуры шести типов и 64 клетки, по которым они ходят. После каких-то четырех первых ходов число возможных дальнейших позиций достигает 288 млрд. Даже самые сильные игроки в мире не в состоянии найти идеальный ход. Они полагаются на интуицию, чтобы найти тот, который окажется достаточно хорошим. Мы можем делать то же самое при помощи алгоритмов. Эвристический метод, или просто эвристика, — это метод, который приводит к решению, не гарантируя, что оно — лучшее или оптимальное. Эвристические алгоритмы помогут, когда методы вроде полного перебора или поиска с возвратом оказываются слишком медленными. Существует много отличных эвристических подходов, но мы сосредоточимся на самом простом: на поиске без возврата.

«Жадные» алгоритмы

Очень распространенный эвристический подход к решению задач — использование так называемых «жадных» алгоритмов. Основная их идея состоит в том, чтобы никогда не откатываться к предыдущим вариантам. Это полная противоположность поиску с возвратом. Иными словами, на каждом шаге мы пытаемся сделать самый лучший выбор, а потом уже не подвергаем его сомнению. Давайте испытаем эту стратегию, чтобы по-новому решить задачу о рюкзаке (из раздела «Полный перебор» ).

Жадный грабитель и рюкзак Грабитель пробирается в ваш дом, чтобы украсть предметы, которые вы хотели продать. Он решает использовать ваш рюкзак, чтобы унести в нем украденное. Что он возьмет? Имейте в виду, что чем быстрее он уйдет, тем меньше вероятность, что его поймают с поличным.

В сущности, оптимальное решение здесь должно быть ровно таким же, что и в задаче о рюкзаке. Однако у грабителя нет времени для перебора всех комбинаций упаковки рюкзака, ему некогда постоянно откатываться назад и вынимать уже уложенные в рюкзак вещи! Жадина будет совать в рюкзак самые дорогие предметы, пока не заполнит его:

function greedy_knapsack(items, max_weight)

    bag_weight ← 0

    bag_items ← List.new

    for each item in sort_by_value(items)

        if max_weight ≤ bag_weight + item.weight

            bag_weight ← bag_weight + item.weight

            bag_items.append(item)

    return bag_items

Здесь мы не принимаем во внимание то, как наше текущее действие повлияет на будущие варианты выбора. Такой «жадный» подход позволяет отыскать подборку предметов намного быстрее, чем метод полного перебора. Однако он не дает никакой гарантии, что общая стоимость подборки окажется максимальной.

В вычислительном мышлении жадность — это не только смертный грех. Будучи добропорядочным торговцем, вы, возможно, тоже испытываете желание напихать в рюкзак всего побольше или очертя голову отправиться в поездку.

Снова коммивояжер Коммивояжер должен посетить n заданных городов и закончить маршрут в той точке, откуда он его начинал. Какой план поездки позволит минимизировать общее пройденное расстояние?

Как мы убедились в разделе «Комбинаторика» (см. главу 1), число возможных комбинаций в этой задаче демонстрирует взрывной рост и достигает неприлично больших величин, даже если городов всего несколько. Найти оптимальное решение задачи коммивояжера с тысячами городов — чрезвычайно дорого (а то и вовсе невозможно). И тем не менее вам нужен маршрут. Вот простой «жадный» алгоритм для этой задачи:

1) посетить ближайший город, где вы еще не были;

2) повторять, пока не объедете все города.

 

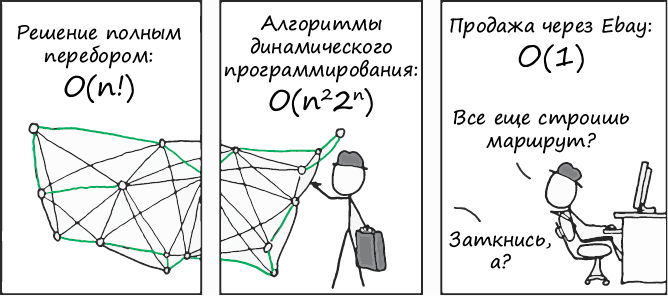
Рис. 3.9. Задача коммивояжера

Можете ли вы придумать более хороший эвристический алгоритм, чем тот, что использует «жадный» подход? Специалисты по информатике вовсю ломают голову над этим вопросом.

Когда жадность побеждает силу

Выбирая эвристический алгоритм вместо классического, вы идете на компромисс. Насколько далеко от идеального решения вы можете отойти, чтобы результат все еще удовлетворял вас? Это зависит от конкретной ситуации.

Впрочем, даже если вам непременно требуется найти идеальный вариант, не стоит сбрасывать эвристику со счетов. Эвристический подход иногда приводит к самому лучшему решению. Например, вы можете разработать «жадный» алгоритм, способный найти такое же решение, что и алгоритм полного перебора. Давайте посмотрим, как такое осуществляется.

Электрическая сеть Поселки в удаленном районе не были электрифицированы, но вот в одном из них начали строить электростанции. Энергия пойдет от поселка к поселку по линиям электропередач. Как включить все поселки в сеть, используя минимум проводов?

Данная задача может быть решена очень просто.

1. Среди поселков, еще не подключенных к сети, выбрать тот, который находится ближе всех к электрифицированному поселку, и соединить их.

2. Повторять, пока все поселки не будут подключены.

 

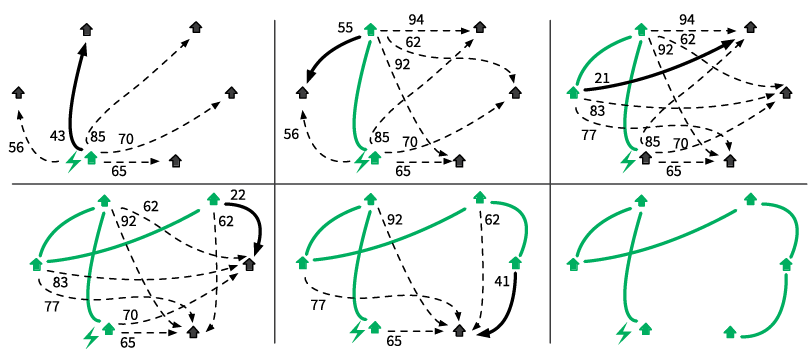
Рис. 3.10. Решение задачи об электрической сети с «жадными» вариантами выбора

На каждом шаге мы выбираем для соединения пару поселков, которая на текущий момент выглядит самой лучшей. Несмотря на то что мы не анализируем, как этот вариант влияет на будущие возможности выбора, присоединение самого близкого поселка без электричества — всегда правильный выбор. Здесь нам повезло: структура задачи идеально подходит для решения «жадным» алгоритмом. В следующем разделе мы увидим структуры задач, для решения которых нужна стратегия великих полководцев.

3.6. Разделяй и властвуй

Когда силы врага раздроблены на небольшие группы, его проще победить. Цезарь и Наполеон управляли Европой, разделяя и завоевывая своих врагов. При помощи той же стратегии вы можете решать задачи — в особенности задачи с оптимальной подструктурой, то есть такие, которые легко делятся на подобные, но меньшие подзадачи. Их можно дробить снова и снова, пока подзадачи не станут простыми. Затем их решения объединяются — так вы получаете решение исходной задачи.

Разделить и отсортировать

Если у нас есть большой список, который нужно отсортировать, мы можем разделить его пополам: каждая половина становится подзадачей сортировки. Затем решения подзадач (то есть отсортированные половины списка) можно объединить в конечное решение при помощи алгоритма слияния. Но как отсортировать эти две половины? Их тоже можно разбить на подзадачи, отсортировать и объединить.

Новые подзадачи будут также разбиты, отсортированы и объединены. Процесс разделения продолжаем, пока не достигнем базового случая: списка из одного элемента. Такой список уже отсортирован!

Этот изящный рекурсивный алгоритм называется сортировкой слиянием. Как и для последовательности Фибоначчи (см. раздел «Рекурсия»), дерево рекурсивных вызовов помогает увидеть, сколько раз функция merge_sort вызывает саму себя (рис. 3.11).

function merge_sort(list)

    if list.length = 1

        return list

    left ← list.first_half

    right ← list.last_half

    return merge(merge_sort(left),

                 merge_sort(right))

Теперь давайте найдем временную сложность сортировки слиянием. Для этого сначала подсчитаем операции, выполняемые на каждом отдельном шаге разбиения, а затем — общее количество шагов.

Подсчет операций. Допустим, у нас есть большой список размером n. При вызове функция merge_sort выполняет следующие операции:

• разбивает список на половины, что не зависит от размера списка O(1);

• вызывает функцию merge (из раздела «Итерация» мы знаем, что merge имеет сложность O(n);

• делает два рекурсивных вызова merge_sort, которые не учитываются.

Поскольку мы оставляем только доминирующий член и не учитываем рекурсивные вызовы, временная сложность функции составляет O(n). Теперь подсчитаем временную сложность каждого шага разбиения.

Шаг разбиения 1. Функция merge_sort вызывается для списка из n элементов. Временная сложность этого шага составляет O(n).

 

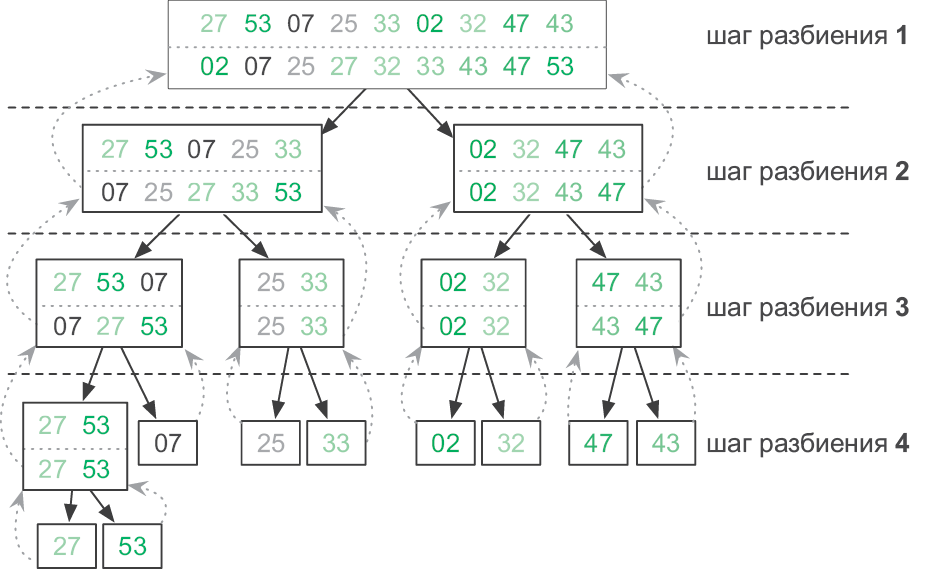
Рис. 3.11. Демонстрация сортировки слиянием. Прямоугольники показывают отдельные вызовы merge_sort, при этом входные данные находятся вверху, а выходные — внизу

Шаг разбиения 2. Функция merge_sort вызывается дважды, каждый раз для 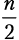элементов. Мы получаем .

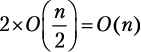Шаг разбиения 3. Функция merge_sort вызывается четыре раза, каждый раз для 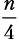элементов: .

 

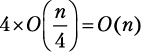Шаг разбиения x. Функция merge_sort вызывается 2x раз, каждый для списка из 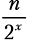элементов: .

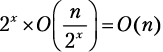Все шаги разбиения имеют одинаковую сложность O(n). Временная сложность сортировки слиянием, следовательно, составляет x × O(n), где x — это количество шагов разбиения, необходимых для полного выполнения алгоритма.

Подсчет шагов. Как вычислить x? Мы знаем, что рекурсивные функции заканчивают вызывать себя, как только достигают своего базового случая. Наш базовый случай — это одноэлементный список. Мы также увидели, что шаг разбиения x работает на списках из 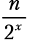элементов. Потому:

 

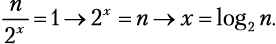
Если вы не знакомы с функцией log2, то не робейте! x = log2 n — это просто еще один способ написать 2x = n. Программисты любят логарифмический рост.

Посмотрите, как медленно растет количество требуемых шагов разбиения с увеличением общего числа сортируемых элементов (табл. 3.1).

Таблица 3.1. Количество шагов разбиения, требуемых для списков разных размеров

Размер списка (n)	log2 n	Требуемое количество шагов разбиения
10	3,32	4
100	6,64	7
1024	10,00	10
1 000 000	19,93	20
1 000 000 000	29,89	30

Временная сложность сортировки слиянием, следовательно, составляет log2 n × O(n) = O(n log n). Это колоссальное улучшение по сравнению с сортировкой выбором O(n2). Помните разницу в производительности между линейно-логарифмическими и квадратичными алгоритмами, которые мы видели в предыдущей главе на рис. 2.4? Даже если предположить, что алгоритм O(n2) будет обрабатываться быстрым компьютером, в конечном счете он все равно окажется медленнее, чем алгоритм O(n log n) на слабой машине (табл. 3.2).

Убедитесь сами: напишите алгоритмы сортировки с линейно-логарифмической и квадратичной сложностью, а затем сравните их эффективность на примере случайных списков разного размера. Когда объемы входных данных огромны, такие улучшения часто оказываются необходимы.

А теперь давайте разделим и осилим задачи, в отношении которых мы раньше применяли полный перебор.

Таблица 3.2. В случае больших объемов входных данных алгоритмы O(n log n) выполняются намного быстрее алгоритмов O(n2), запущенных на компьютерах, в 1000 раз более производительных

Объем данных	Квадратичный	Логлинейный
196 (число стран в мире)	38 мс	2 с
44 000 (число аэропортов в мире)	32 минуты	12 минут
171 000 (число слов в словаре английского языка)	8 часов	51 минута
1 млн (число жителей Гавайев)	12 дней	6 часов
19 млн (число жителей штата Флорида)	11 лет	6 дней
130 млн (число книг, опубликованных за все время)	500 лет	41 день
4,7 млрд (число страниц в Интернете)	700 000 лет	5 лет

Разделить и заключить сделку

Для задачи о самой лучшей сделке (см. раздел «Полный перебор» ) подход «Разделяй и властвуй» оказывается лучше, чем решение «в лоб». Разделение списка цен пополам приводит к двум подзадачам: нужно найти лучшую сделку в первой половине и лучшую сделку во второй. После этого мы получим один из трех вариантов:

1) лучшая сделка с покупкой и продажей в первой половине;

2) лучшая сделка с покупкой и продажей во второй половине;

3) лучшая сделка с покупкой в первой половине и продажей во второй.

 

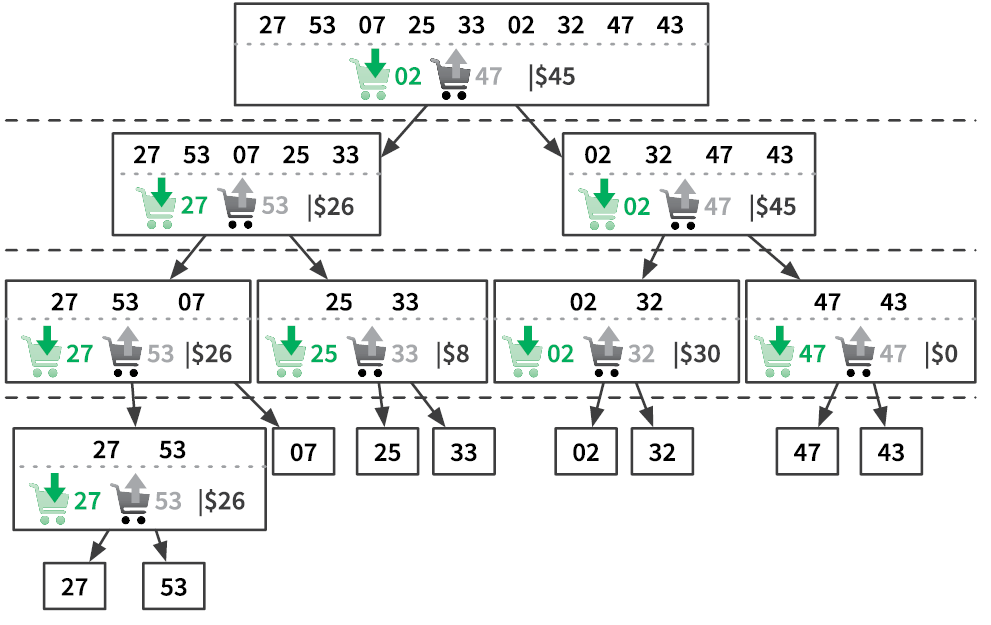
Рис. 3.12. Демонстрация выполнения функции trade. Прямоугольники показывают отдельные вызовы trade с входными и выходными данными

Первые два случая — это решения подзадач. Третий легко находится: нужно найти самую низкую цену в первой половине списка и самую высокую во второй. Если на входе данные всего за один день, то единственным вариантом становится покупка и продажа в этот день, что приводит к нулевой прибыли.

function trade(prices)

    if prices.length = 1

        return 0

    former ← prices.first_half

    latter ← prices.last_half

    case3 ← max(latter) - min(former)

    return max(trade(former), trade(latter), case3)

Функция trade выполняет тривиальное сравнение, разбивает список пополам и находит максимум и минимум в его половинах. Поиск максимума или минимума в списке из n элементов требует просмотра всех n элементов, таким образом, отдельный вызов trade стоит O(n).

Вы наверняка заметите, что дерево рекурсивных вызовов функции trade (рис. 3.12) очень похоже на такое же для сортировки слиянием (рис. 3.11). Оно тоже имеет log2 n шагов разбиения, каждый стоимостью O(n). Следовательно, функция trade тоже имеет сложность O(n log n) — это огромный шаг вперед по сравнению со сложностью O(n2) предыдущего подхода, основанного на полном переборе.

Разделить и упаковать

Задачу о рюкзаке (см. раздел «Полный перебор» ) тоже можно разделить и тем самым решить. Если вы не забыли, у нас n предметов на выбор. Мы обозначим свойство каждого из них следующим образом:

• wi — это вес i-го предмета;

• vi — это стоимость i-го предмета.

Индекс i предмета может быть любым числом от 1 до n. Максимальный доход для вместимости c рюкзака с уже выбранными n предметами составляет K(n, c). Если рассматривается дополнительный предмет i = n + 1, то он либо повысит, либо не повысит максимально возможный доход, который становится равным большему из двух значений.

1. K(n, c) — если дополнительный предмет не выбран.

2. K(n, c − wn+1) + vn+1 — если дополнительный предмет выбран.

Случай 1 предполагает отбраковку нового предмета, случай 2 — включение его в набор и размещение среди выбранных ранее вещей, обеспечивая для него достаточное пространство. Это значит, что мы можем определить решение для n предметов как максимум частных решений для n – 1 предметов:

K(n, c) = max (K(n − 1, c),

K(n − 1, c − wn) + vn).

Вы уже достаточно знаете и должны легко преобразовать эту рекурсивную формулу в рекурсивный алгоритм. Рисунок 3.13 иллюстрирует, как рекурсивный процесс решает задачу. На схеме выделены одинаковые варианты — они представляют идентичные подзадачи, вычисляемые более одного раза. Далее мы узнаем, как предотвратить такие повторные вычисления и повысить производительность.

 

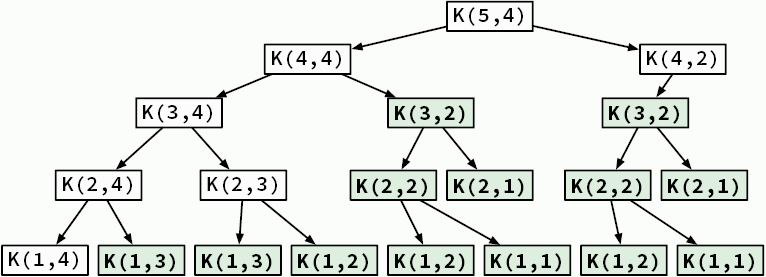
Рис. 3.13. Решение задачи о рюкзаке с 5 предметами и вместимостью рюкзака 4. Предметы под номерами 5 и 4 весят две единицы, остальные — одну единицу

3.7. Динамическое программирование

Во время решения задачи иногда приходится выполнять одни и те же вычисления многократно. Динамическое программирование позволяет идентифицировать повторяющиеся подзадачи, чтобы можно было выполнить каждую всего один раз. Общепринятый метод, предназначенный для этого, основан на запоминании и имеет «говорящее» название.

Мемоизация Фибоначчи

Помните алгоритм вычисления чисел Фибоначчи? Его дерево рекурсивных вызовов (см. рис. 3.3) показывает, что fib(3) вычисляется многократно. Мы можем это исправить, сохраняя результаты по мере их вычисления и делая новые вызовы fib только для тех вычислений, результатов которых еще нет в памяти (рис. 3.14). Этот прием

 

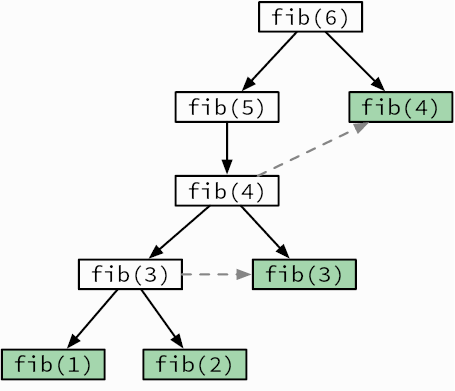
Рис. 3.14. Дерево рекурсивных вызовов для dfib. Зеленые прямоугольники обозначают вызовы, не выполняемые повторно

многократного использования промежуточных результатов называется мемоизацией. Он повышает производительность функции fib:

M ← [0  0; 2  2]

function dfib(n)

    if n not in M

        M[n] ← dfib(n-1) + dfib(n-2)

    return M[n]

Мемоизация предметов в рюкзаке

Очевидно, что в дереве рекурсивных вызовов для задачи о рюкзаке (см. рис. 3.13) имеются многократно повторяемые вызовы. Применение того же самого приема, который мы использовали для функции Фибоначчи, позволяет избежать этих повторных вызовов и в итоге уменьшить объем вычислений (рис. 3.15).

 

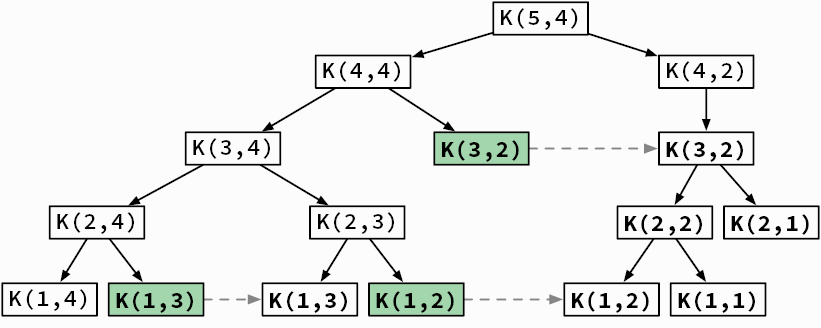
Рис. 3.15. Рекурсивное решение задачи о рюкзаке при помощи мемоизации

Динамическое программирование позволяет добиться от чрезвычайно медленного программного кода приемлемого быстродействия. Тщательно анализируйте свои алгоритмы, чтобы убедиться, что в них нет повторных вычислений. Как мы увидим далее, иногда перекрывающиеся подзадачи могут порождать проблемы.

Лучшая сделка снизу вверх

Дерево рекурсии для функции trade (см. рис. 3.12) не имеет повторных вызовов, и все равно делает повторные вычисления. Он просматривает вход, чтобы найти максимальное и минимальное значения. Затем входные данные разбиваются на две части, и рекурсивные вызовы анализируют их снова, чтобы найти максимум и минимум в каждой половине. Нам нужен другой принцип, для того чтобы избежать этих повторных проходов.

До сих пор мы использовали нисходящий подход, где объем входных данных постепенно уменьшается, пока не будут достигнуты базовые случаи. Но мы также можем пойти снизу вверх: сначала вычислить базовые случаи, а затем раз за разом собирать их, пока не получим общий результат. Давайте решим задачу о лучшей сделке (см. раздел «Полный перебор» ) таким способом.

Пусть P(n) — это цена в n-й день, а B(n) — лучший день для покупки при продаже в n-й день. Если мы продаем в первый день, то купить у нас получится только тогда же, других вариантов нет, поэтому B(1) = 1. Но если мы продаем во второй день, B(2) может равняться 1 либо 2:

• P(2) < P(1) ! B(2) = 2 (купить и продать в день 2);

• P(2) ≥ P(1) ! B(2) = 1 (купить в день 1, продать в день 2).

День с самой низкой ценой перед днем 3, но не в день 3 — это B(2) . Потому для B(3):

• P(3) < цена в день B(2) —> B(3) = 3.

• P(3) ≥ цена в день B(2) —> B(3) = B(2).

Обратите внимание, что день с самой низкой ценой перед днем 4 будет B(3). Фактически для каждого n день с самой низкой ценой перед днем n — B(n – 1). Мы можем это использовать, чтобы выразить B(n) через B(n – 1):

 

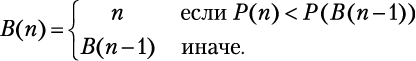
Когда у нас есть все пары [n, B(n)] для для каждого дня n, решением является пара, которая дает самую высокую прибыль. Следующий алгоритм решает задачу, вычисляя все значения B снизу вверх:

function trade_dp(P)

    B[1] ← 1

    sell_day ← 1

    best_profit ← 0

 

    for each n from 2 to P.length

        if P[n] < P[B[n-1]]

            B[n] ← n

        else

            B[n] ← B[n-1]

 

        profit ← P[n] - P[B[n]]

        if profit > best_profit

            sell_day ← n

            best_profit ← profit

 

    return (sell_day, B[sell_day])

Алгоритм выполняет фиксированное число простых операций для каждого элемента входного списка, следовательно, он имеет сложность O(n). Это огромный рывок в производительности по сравнению со сложностью предыдущего алгоритма O(n log n) — и совершенно несравнимо со сложностью O(n2) метода полного перебора. Этот алгоритм также имеет пространственную сложность O(n), поскольку вспомогательный вектор B содержит столько же элементов, что и входные данные. Из приложения IV вы узнаете, как сэкономить память за счет создания алгоритма с пространственной сложностью O(1).

3.8. Ветви и границы

Многие задачи связаны с минимизацией или максимизацией целевого значения: найти кратчайший путь, получить наибольшую прибыль и т.д. Такие задачи называются задачами оптимизации. Когда решением является последовательность вариантов, мы часто используем стратегию ветвей и границ. Ее цель состоит в том, чтобы выиграть время за счет быстрого обнаружения и отбрасывания плохих вариантов. Чтобы понять, каким образом они ищутся, мы сначала должны разобраться в понятиях «верхняя граница» и «нижняя граница».

Верхние и нижние границы

Границы обозначают диапазон значения. Верхняя граница устанавливает предел того, каким высоким оно может быть. Нижняя граница — это наименьшее значение, на которое стоит надеяться; она ­гарантирует, что любое значение либо равно ей, либо ее превышает.

Мы порой легко находим решения, близкие к оптимальным: короткий путь — но, возможно, не самый короткий; большая прибыль — но, возможно, не максимальная. Они дают границы оптимального решения. К примеру, любой короткий маршрут из одной точки в другую никогда не будет короче расстояния между ними по прямой. Следовательно, расстояние по прямой является нижней границей самого короткого пути.

В задаче о жадном грабителе и рюкзаке (см. раздел «Эвристические алгоритмы» ) прибыль, полученная посредством greedy_knapsack, является нижней границей оптимальной прибыли (она может быть или не быть близкой к оптимальной прибыли). Теперь представим версию задачи о рюкзаке, в которой вместо предметов у нас сыпучие материалы, и мы можем насыпать их в рюкзак, сколько поместится. Эта версия задачи решается «жадным» способом: просто продолжайте насыпать материалы с самым высоким соотношением стоимости и веса:

function powdered_knapsack(items, max_weight)

    bag_weight ← 0

    bag_items ← List.new

    items ← sort_by_value_weight_ratio(items)

    for each i in items

        weight ← min(max_weight - bag_weight,

                     i.weight)

        bag_weight ← bag_weight + weight

        value ← weight * i.value_weight_ratio

        bagged_value ← bagged_value + value

        bag_items.append(item, weight)

    return bag_items, bag_value

Добавление ограничения неделимости предметов только уменьшит максимально возможную прибыль, потому что нам придется менять последнюю уложенную в рюкзак вещь на что-то подешевле. Это означает, что powdered_knapsack дает верхнюю границу оптимальной прибыли с неделимыми предметами.

Ветви и границы в задаче о рюкзаке

Мы уже убедились, что поиск оптимальной прибыли в задаче о рюкзаке требует дорогих вычислений O(n2). Однако мы можем быстро получить верхние и нижние границы оптимальной прибыли при помощи функций powdered_knapsack и greedy_knapsack. Давайте попробуем это сделать на примере задачи о рюкзаке (табл. 3.3).

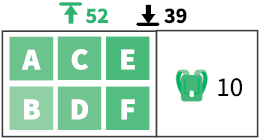
Таблица 3.3. Верхняя и нижняя границы в задаче о рюкзаке

Предмет	Стоимость	Вес	Соотношение стоимости и веса	Макс. вместимость
A	20	5	4,00
B	19	4	4,75
C	16	2	8,00	10
D	14	5	2,80
E	13	3	4,33
F	9	2	4,50

Рисунок справа иллюстрирует ситуацию перед началом заполнения рюкзака. В первом поле находятся неупакованные предметы, которые нам предстоит рассмотреть. Второе поле представляет свободное место в рюкзаке и предметы, которые уже уложены. Выполнение функции greedy_knapsack дает прибыль 39, а powdered_knapsack — 52,66. Это означает, что оптимальная прибыль находится где-то посередине. Как мы знаем из раздела «Разделяй и властвуй», эта задача с n предметами делится на две подзадачи с n – 1 предметами. Первая подзадача подразумевает, что предмет A был взят, вторая — что он не был взят:

 

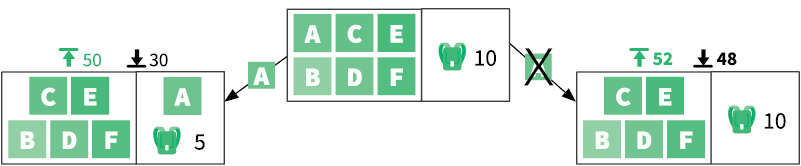
Мы вычисляем верхнюю и нижнюю границы для этих двух подзадач. Каждая имеет нижнюю границу, равную 48: теперь мы знаем, что оптимальное решение находится между 48 и 52. Давайте рассмотрим подзадачу справа, поскольку у нее более интересные границы:

 

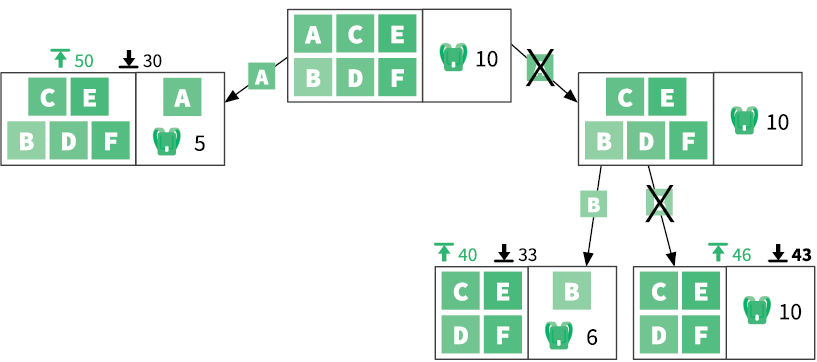
Крайняя левая подзадача имеет самую многообещающую верхнюю границу. Давайте продолжим наш анализ и выполним разбиение этой подзадачи:

 

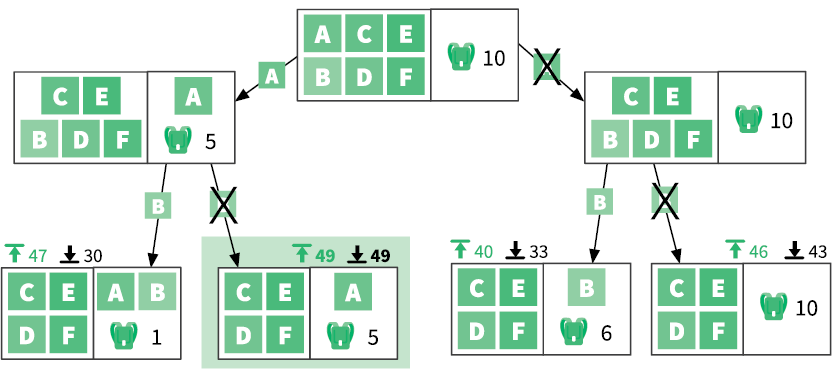
Теперь мы можем сделать важные выводы. Выделенная цветом подзадача имеет нижнюю границу 49, которая равна ее верхней границе. Это означает, что оптимальная прибыль здесь должна равняться строго 49. Кроме того, обратите внимание, что 49 больше верхних границ во всех других ветвях, которые были проанализированы. Никакая другая ветвь не даст большую прибыль, чем 49, а значит, мы можем исключить их все из дальнейшего поиска.

Рациональное использование верхних и нижних границ позволило нам найти оптимальную прибыль, выполнив совсем немного вычислений. Мы динамически адаптировали наше пространство поиска по мере анализа возможностей.

Вот общие принципы работы метода ветвей и границ:

1) разделить задачу на подзадачи;

2) найти верхние и нижние границы каждой подзадачи;

3) сравнить границы подзадач всех ветвей;

4) выбрать самую многообещающую задачу и вернуться к шагу 1.

Если вы помните, стратегия поиска с возвратом (см. соответствующий раздел) тоже позволяет найти решение без обследования каждого возможного варианта. В случае поиска с возвратом мы исключаем пути, изучив каждый из них так далеко, как это возможно, и останавливаемся, когда нас устраивает решение. В случае же с методом ветвей и границ мы заранее определяем бесперспективные пути и не тратим впустую энергию на их обследование.

Подведем итоги

Решение задач, в сущности, представляет собой перемещение по пространству возможностей с целью найти правильный вариант. Мы узнали несколько способов, как это делается. Самый простой — полный перебор, то есть последовательная проверка каждого элемента в пространстве поиска.

Мы научились систематически делить задачи на меньшие, получая большое увеличение производительности. Многократное деление задач часто бывает сопряжено с решением проблем, вызванных одинаковыми подзадачами. В этих случаях важно использовать динамическое программирование, чтобы избежать повторных вычислений.

Мы убедились, что поиск с возвратом позволяет оптимизировать некоторые алгоритмы, основанные на полном переборе. Значения верхних и нижних границ (там, где их можно получить) позволяют ускорить поиск решения, для этого используется метод ветвей и границ. А когда стоимость вычисления оптимального решения оказывается неприемлемой, следует использовать эвристический алгоритм.

Все стратегии, с которыми мы познакомились, предназначены для работы с данными. Далее мы узнаем самые распространенные способы организации данных в памяти компьютера и как они влияют на производительность операций.

Полезные материалы

• Клейнберг Дж., Традос Е. Алгоритмы: разработка и применение. СПб.: Питер, 2017.

• Выбор стратегии проектирования алгоритмов (Choosing Algorithm Design Strategy, Shailendra Nigam, см. ).

• Динамическое программирование (Dynamic programming, by Umesh V. Vazirani, см. ).