14
Бесконечно малые величины

Тесная зависимость математики с физикой недолго оставалась уникальным явлением. Начиная с XVII в. эти две дисциплины постоянно обмениваются идеями, обогащая друг друга. Поскольку физика основывается на формулах, каждое новое открытие требует математического подтверждения. Существуют ли уже соответствующие формулы или их еще предстоит изобрести? В последнем случае перед математиками встает задача создать новые теории на заказ. Так физика становится для них одним из самых главных источников вдохновения.

Развитие ньютоновской теории гравитации стало одним из первых катализаторов развития инновационной математики. Чтобы понять это, вернемся к следу кометы Галлея. Знать силу, которая притягивает ее к Солнцу, это уже что-то, но как, исходя из этой информации, вычислить ее траекторию и другую полезную информацию, такую, как, например, ее положение в конкретную дату или точный период обращения?

Один из классических вопросов, на которые предстоит ответить, – это, в частности, определение пройденного расстояния в зависимости от скорости. Если я скажу вам, что скорость перемещения кометы в пространстве равна 2000 метров в секунду, и спрошу, какое расстояние она пройдет за одну минуту, найти ответ будет достаточно просто. За одну минуту комета пройдет 60 раз по 2000 метров, то есть 120 000 м, или 120 км. Проблема заключается в том, что в реальности все намного сложнее. Скорость кометы не постоянная, а меняется с течением времени. На своем афелии, то есть в самой дальней точке от Солнца, она составляет 800 метров в секунду, в то время как в перигелии, ближе всего к Солнцу, она составляет 50 000 метров в секунду. Большая разница!

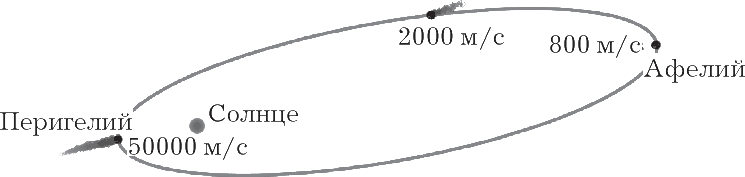
И вся сложность заключается в том, что между этими двумя крайностями комета не разгоняется постепенно и никогда не движется на одной скорости. В определенный момент комета движется со скоростью 2000 метров в секунду, но она не постоянна. Мгновение до скорость была немного больше, скажем, 2000,001 метра в секунду и уже через долю секунды после она уже равна 1999,999 метра в секунду. Невозможно найти такой промежуток времени, даже самый крошечный, в котором комета сохраняет постоянную скорость! Как при таких условиях точно рассчитать расстояние, которое она пройдет?

Для того чтобы ответить на этот вопрос, математики прибегают к методу, который странным образом напоминает способ, использовавшийся две тысячи лет назад Архимедом для вычисления числа π. Подобно тому как ученый из Сиракуз сопоставлял круг и многоугольники с большим количеством сторон, можно приблизительно рассчитать траекторию движения кометы, разбив ее путь на все более и более короткие промежутки. Можно, например, предположить, что комета поддерживает постоянную скорость 800 метров в секунду определенный интервал времени, а затем начинает двигаться на скорости 900 метров в секунду еще один интервал времени и так далее. Траектория, рассчитанная таким образом, не будет точной, но может рассматриваться как приближенная. Для того чтобы увеличить точность расчетов, достаточно взять за основу более короткие интервалы. Вместо того чтобы рассматривать интервалы 100 метров в секунду, можно сократить их до 10,1 или даже 0,1 метра в секунду. Чем более мелкие отрезки скорости будут выбраны для расчетов, тем полученная траектория окажется ближе к фактической траектории кометы!

Последовательность приближенных расстояний, пройденных кометой от афелия до перигелия, может выглядеть следующим образом:

Эти числа приведены в астрономических единицах. Другими словами, если мы предположим, что скорость кометы остается неизменной в интервале 100 метров в секунду, расстояние между афелием и перигелием будет равняться 47 астрономическим единицам. Этот результат, разумеется, является грубым приближением. Если уточнить интервал до 10 метров в секунду, искомое расстояние будет равно 42 астрономическим единицам. Отрезки, на которых происходит изменение скорости, сокращаются все больше и больше, расстояние приближается к 38,45 астрономическим единицам. Это предельное значение соответствует фактическому расстоянию, которое проходит комета между двумя крайними точками своего пути.

В некотором смысле этот результат можно назвать полученным с помощью разделения траектории кометы на бесконечное число бесконечно малых интервалов. Данный подход аналогичен методу Архимеда, по которому можно рассчитать число π, представив круг как многоугольник с бесконечным числом бесконечно малых сторон! Проблема этих двух утверждений в определении бесконечности. Этот термин знаком нам еще из рассуждений Зенона, в которых неоднозначное и опасное понятие бесконечности приводило к балансированию на грани парадокса.

Таким образом, есть два варианта: либо полностью отказаться от использования понятия бесконечности, кропотливо изучать проблемы ньютоновской физики с помощью рядов предельных приближений, либо собрать всю волю в кулак и осторожно погрузиться в болото бесконечно малых интервалов. Именно по этому пути пошел Ньютон в «Математических началах натуральной философии». Этого же подхода будет придерживаться немецкий математик Готфрид Вильгельм Лейбниц, который независимо от Ньютона сделал аналогичное открытие, а также доработал некоторые понятия, требовавшие уточнений в рассуждениях Ньютона. Из этих исследований будет рождаться новая отрасль математики, которая получит название «исчисление бесконечно малых величин».

Вопрос об авторстве этой отрасли еще долго обсуждался в последующие годы. В то время как Ньютон был первым, кто начал заниматься исследованиями в этом направлении уже с 1669 г., но слишком долго не предавал гласности результаты своей работы, Лейбниц сформулировал соответствующую теорию и опубликовал свою работу в 1684 г., за три года до «Математических начал натуральной философии». Это переплетение дат привело к возникновению конфликта между английским и немецким научными сообществами, каждое из которых не признало первенство другого и даже предъявляло обвинения в плагиате. Сегодня представляется, что ни один из ученых не знал о существовании подобных исследований, и можно считать, что исчисление бесконечно малых величин было открыто каждым из них самостоятельно.

В самом начале теория не была идеальной. Многим пунктам в исследованиях Ньютона и Лейбница все еще не хватало строгости и обоснованности. Как это уже случилось ранее с мнимыми числами, был сделан вывод, что одни методы работают, а другие – нет, без понимания истинных причин этого.

Так, исчисление бесконечно малых величин становится подобным изучению неизведанной территории, когда на карте помечают важные связующие направления и запретные пути, ведущие к тупикам и парадоксам. В 1748 г. итальянский математик Мария Гаэтана Аньези публикует свою работу под названием «Основы анализа» (от итал. Instituzioni Analitiche), в которой впервые будут описаны накопленные на тот момент знания в области молодой дисциплины. Спустя столетие немецкий математик Бернхард Риман опубликует свою работу с наиболее поздними исследованиями применения этой дисциплины.

С этого момента математики начали повсеместно использовать исчисление бесконечно малых величин и применять его в решении многочисленных вопросов, возникающих в связи с тысячами физических явлений. Эта теория оказалась не просто инструментом, позволяющим решать сложные задачи, но и была удивительно красивой. Наука подобна бесконечной игре в теннис, и эти новые разработки будут постепенно находить применение в других областях, как, например, астрономия.

Бесконечно малые величины будут использоваться в решении любых задач, в которых, по аналогии с движением кометы, присутствуют непрерывно изменяющиеся величины. В метеорологии – для того чтобы моделировать и прогнозировать изменение температуры или атмосферного давления. В океанографии – чтобы следить за океаническими течениями. В аэродинамике – для контроля сопротивления воздуха с крыльями самолета или различными космическими аппаратами. В геологии – для мониторинга состояния мантии Земли и изучения вулканов, землетрясений и, в долгосрочной перспективе, дрейфа материков.

В ходе исследований математики обнаружили в бесконечно малом мире множество необычных результатов, некоторые из которых сильно озадачили их.

Одна из первых идей, как определить бесконечно малый интервал, предлагала выбрать в качестве него точку. Еще Евклид определил точку как наименьший геометрический элемент. При длине, равной 0, точка бесконечно мала. К сожалению, эта идея, такая простая в понимании, не может быть взята за основу. Для того чтобы понять это, посмотрите на этот отрезок, длина которого обозначена как 1.

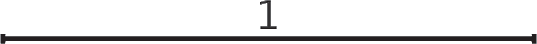
Этот отрезок состоит из бесконечного числа точек, каждая из которых имеет длину, равную 0. Так, можно сказать, что длина отрезка равна бесконечному количеству нулей! На алгебраическом языке это можно записать, как ∞ × 0 = 1, где ∞ обозначает бесконечность. Проблема этого вывода заключается в том, что если мы теперь рассмотрим отрезок, длина которого равна 2, то получится, что она тоже состоит из бесконечного числа точек, что в этот раз соответствует равенству ∞ × 0 = 2. Как может получиться так, что одинаковые расчеты приводят к двум различным результатам? Так, изменяя длину отрезка, мы можем также рассчитать, что произведение ∞ × 0 равно 3, 1000 или даже π!

Исходя из этого мы вынуждены сделать следующий вывод: используемые определения нуля и бесконечности в данном контексте недостаточно точны и не могут быть использованы в дальнейшем. Такие произведения как ∞ × 0, результат которых изменяется в зависимости от его интерпретации, называют неопределенной формой. Невозможно использовать эти формы в алгебраических вычислениях, так как мы сразу столкнемся с тысячами парадоксов! Если бы мы стали применять умножение ∞ × 0, то тем самым пришлось бы признать, что 1 равно 2 и т. д. Короче говоря, необходимо поступать иначе.

Сделаем вторую попытку. Если бесконечно малый интервал не может быть точкой, это может быть отрезок, ограниченный двумя точками, расположенными бесконечно близко друг к другу. Идея привлекательная, но мы снова сталкиваемся с проблемой, потому что таких отрезков не существует. Расстояние между двумя точками может быть сколь угодно малым, но всегда будет иметь положительную длину. Отрезки длиной в сантиметр, миллиметр, одну миллиардную миллиметра или даже меньше, конечно, очень малы, но ни в коем случае не бесконечно малы. Иными словами, две точки никогда не будут соприкасаться.

Есть что-то очень обескураживающее в этом заявлении. Когда вы рисуете непрерывную линию, например отрезок, в ней нет никаких промежутков, и тем не менее точки, которые составляют ее, не соприкасаются! Ни одна точка не соприкасается с другими. Отсутствие отверстий в линии является всего лишь следствием того, что она состоит из бесконечно малых точек. И если определять точки линии по их взаимосвязям, это же явление можно представить в алгебраической форме следующим образом: два различных числа никогда не идут подряд, всегда есть бесконечное множество других чисел, которые находятся между ними. Между числами 1 и 2 находится 1,5. Между числами 1 и 1,1 находится 1,05. А между числами 1 и 1,0001 есть 1,00005. Так можно продолжать до бесконечности. С числом 1, как и со всеми другими, не «соприкасаются» другие числа. Однако бесконечная совокупность бо́льших и меньших чисел обеспечивает непрерывность последовательности.

После двух неудачных попыток нам приходится признать, что во множестве классических чисел по определению невозможно выделить бесконечно малые величины. Эти неуловимые числа не могут быть приравнены к нулю и также меньше всех существующих положительных чисел, поэтому придется отдельно описывать их с самого начала! Над этим работали Лейбниц и ученые, которые последовали его примеру в исчисления бесконечно малых величин. Потребовалось три столетия для того, чтобы сформулировать правила расчета, которые применяются к этим новым числам, и определить сферу их действия. Таким образом, с XVII по XX в. был разработан целый арсенал теорем, позволяющих эффективно решать задачи с бесконечно малыми величинами.

Числа, которые не существуют в действительности, тем не менее могут быть использованы в качестве промежуточного результата? Это вам ничего не напоминает? Так уже было с отрицательными и мнимыми числами. Но, как это часто бывает, процесс внедрения длится долго и не всегда можно предсказать исход. В 1960-е годы американский математик Абрахам Робинсон разработал новую модель, в которой бесконечно малые величины рассматривались как отдельная группа чисел. Тем не менее в отличие от мнимых чисел, бесконечно малые величины и сегодня, в начале XXI в., фактически не относят к действительным числам. Нестандартная модель анализа Робинсона вызывает множество противоречий и редко используется на практике.

Возможно, в будущем нас неизбежно ждут открытия, исследования, теоремы, созданные на основе этой нестандартной теории. А может быть, наоборот, у нее нет потенциала, чтобы стать доминирующей моделью, и бесконечно малые величины никогда не сравнятся по значимости со своими прославленными предшественниками – отрицательными и мнимыми числами. Нестандартный анализ, безусловно, интересен, но, возможно, несет в себе слишком мало пользы, чтобы продолжительное время поддерживать энтузиазм. Прошло всего несколько десятилетий с момента разработки Робинсоном своей модели, и математикам будущего еще предстоит решить ее судьбу.

Среди наиболее успешных разработок исчисления бесконечно малых величин можно выделить теорию меры, разработанную в начале XX в. французским математиком Анри Леоном Лебегом – одно из самых любопытных направлений. Возникает вопрос: можно ли с использованием бесконечно малых величин создать новые геометрические фигуры, которые нельзя нарисовать с помощью циркуля и линейки. Ответ: да, и эти новые фигуры будут созданы в течение нескольких лет в соответствии с законами классической геометрии. Возьмем, например, отрезок, размеченный от 0 до 10.

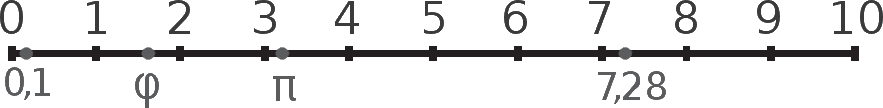
По аналогии с Декартовой системой координат, эта разметка позволяет соотнести точку на отрезке с любым числом от 0 до 10. На этом отрезке можно отдельно выделить точки, имеющие конечное десятичное значение (например, 0,1 или 7,28), и числа с бесконечным числом цифр после запятой (например, число π или число золотого сечения φ). Что произойдет, если мы разделим отрезок по этому принципу? Другими словами, если мы выделим темным цветом точки первой категории и светлым цветом – второй, как будут выглядеть темная и светлая геометрические фигуры соответственно?

Не так просто ответить на этот вопрос, потому что эти две категории чисел можно продолжать до бесконечности. Если взять даже самый малый диапазон чисел, то он всегда будет содержать как темные, так и светлые точки. Между двумя светлыми точками всегда есть по крайней мере одна темная, а между двумя темными точками всегда есть по крайней мере одна светлая. Две фигуры, таким образом, напоминают бесконечно тонкие нити, которые идеально связаны друг с другом.

Отрезок от 0 от 10 делится на две части: слева – имеющие конечное десятичное значение; справа – числа с бесконечным числом цифр после запятой

Представленное выше изображение, конечно же, неправильное. Это всего лишь грубая визуализация, и элементы, нарисованные очень мелко, на самом деле не бесконечно малы.

Невозможно точно изобразить фигуры, которые могут быть описаны только с помощью алгебры или рассуждений.

В связи с этим возникает вопрос: как измерить эти фигуры? Так, начальный отрезок имеет длину, равную 10. Должны ли две образующие его фигуры иметь одинаковую длину? Станет ли каждая из них иметь длину 5, или одна окажется больше другой? Ответ, который будет найден математиками, поистине удивителен.

Абсолютно вся длина занята фигурой, составленной из чисел с бесконечным количеством знаков после запятой. Фигура, состоящая из светлых точек, будет равна в совокупности 10, а фигура, состоящая из темных точек – 0. Хотя обе фигуры кажутся одинаковым образом переплетенными между собой, на выбранном отрезке бесконечно больше светлых точек, чем темных!

Используя систему координат Декарта, эти рассеянные фигуры могут быть представлены в двух– или трехмерном пространстве. Например, мы можем представить совокупность точек в виде квадрата, координаты которого имеют бесконечное количество значений.

Еще раз обратим внимание, что это всего лишь грубое упрощение, которое дает только смутное представление о том, как может выглядеть бесконечное множество элементов.

Измерение рассеянных элементов приведет к одному из самых удивительных математических результатов: несмотря на все усилия математиков, занимающихся решением этой проблемы, некоторые из этих фигур будет невозможно измерить.

Эта их особенность доказана в 1924 г. Стефаном Банахом и Альфредом Тарским, который обнаружил контрпример принципа мозаики.

Они нашли способ разделить шар на пять частей таким образом, чтобы потом можно было собрать из них два абсолютно таких же шара как первый без единого промежутка!

Пять полученных фигур представляют собой рассеянные фигуры с бесконечно малыми составляющими. Если бы полученные мозаичные части из примера Банаха – Тарского были измеримы, то сумма их объемов была бы одновременно равна как объему шара, из которого они были получены, так и объемам двух шаров, которые могут быть сформированы из них. Этот факт позволяет сделать следующий вывод: даже понятие объема теряет смысл в отношении подобных фигур.

На самом деле выводы Банаха и Тарского гораздо обширнее, так как они показывают, что если рассмотреть две классические геометрические фигуры в трех измерениях, то, разбив первую фигуру на определенное количество рассеянных частей, можно будет собрать аналогичную ей вторую фигуру. Можно, например, разделить на множество частей шар размером с горошину и собрать из них совокупность шаров размером с Солнце без единого промежутка! Описанное явление часто ошибочно называют парадоксом Банаха – Тарского из-за его кажущейся на первый взгляд нелогичности. Однако это не парадокс, а теорема, существование которой возможно благодаря свойствам рассеянных фигур, обеспечивающим логичность рассуждений и отсутствие противоречий!

Разумеется, разделение на бесконечное количество бесконечно малых частей на практике недостижимо. Рассеянные фигуры сегодня остаются в числе необычных математических явлений, не используемых на практике. Кто знает, наступит ли тот день, когда они начнут применяться для решения определенных задач?