Книга: На плечах гигантов
Назад: I. Кинематическая часть
Дальше: Вопросы космологии и общая теория относительности
Основы общей теории относительности
А. Принципиальные соображения о постулате относительности
§ 1. Замечания к специальной теории относительности
В основе специальной теории относительности лежит следующий постулат, которому удовлетворяет также и механика Галилея – Ньютона.
Если система координат К выбрана таким образом, что физические законы в ней справедливы в своей простейшей форме, то те же самые законы справедливы и во всякой другой координатной системе К’, которая движется равномерно и прямолинейно относительно К. Будем называть этот постулат «специальным принципом относительности». Словом «специальный» подчеркнем то обстоятельство, что этот принцип ограничивается случаем, когда система К’ совершает относительно системы К равномерное и прямолинейное движение, и что равноценность систем К’ и К не распространяется на случай неравномерного движения системы К’ относительно К.
Итак, специальная теория относительности отличается от классической механики не только постулатом относительности, но и в основном постулатом постоянства скорости света в пустоте, из которого при объединении его со специальным принципом относительности известным образом вытекает относительность одновременности, преобразование Лоренца и связанные с этим преобразованием законы, касающиеся поведения движущихся твердых тел и часов.
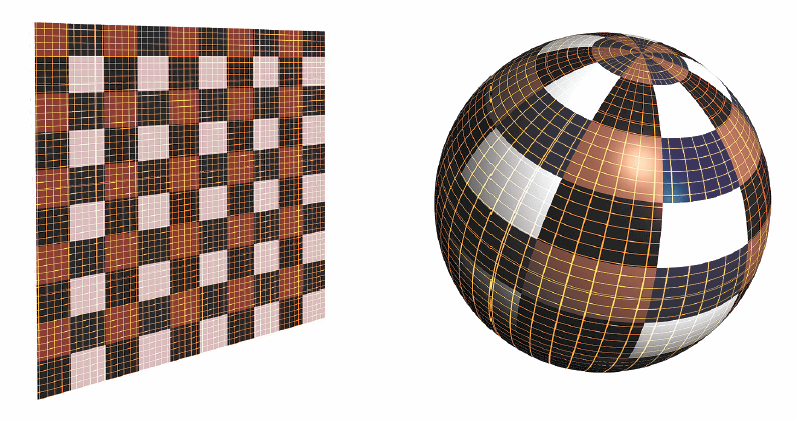
Теоретические истории Вселенной.
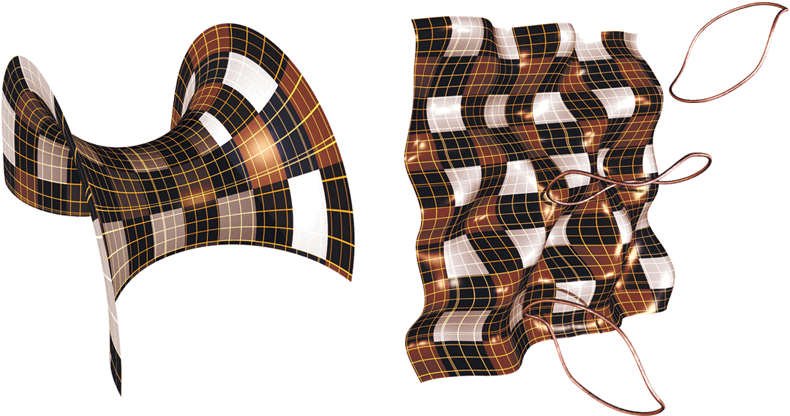
Плоская мембрана (первая слева ) говорит о необходимости определить границы, и таково было представление о Земле, когда ее считали плоской. Если Вселенная уходит на бесконечность, как седловидная поверхность (вторая справа), опять же возникают сложности с определением граничных условий на бесконечности. Если все истории Вселенной в мнимом времени представляют собой замкнутые пространства, подобные поверхности Земли, необходимость определять граничные условия отпадает сама собой. Выходя за рамки теорий Эйнштейна, мы задумываемся о множественных мирах на многомерных бранах.
Несмотря на то что теория пространства и времени испытала под влиянием специальной теории относительности очень глубокое изменение, один важный пункт остался незатронутым. Согласно специальной теории относительности высказывания геометрии имеют значение законов, касающихся возможных относительных положений (покоящихся) твердых тел, а общие положения кинематики – значение законов, описывающих поведение измерительных приборов и часов. При этом двум выбранным материальным точкам покоящегося (твердого) тела всегда соответствует некоторый отрезок вполне определенной длины, независимо как от положения и ориентации тела, так и от времени. Двум отмеченным показаниям стрелки часов, покоящихся относительно некоторой (допустимой) координатной системы, всегда соответствует интервал времени определенной величины, независимо от места и времени. Далее мы увидим, что общая теория относительности не может придерживаться этого простого физического толкования пространства и времени.
§ 2. Об основаниях, которые подсказывают расширение постулата относительности
Классической механике и в неменьшей степени специальной теории относительности свойственен некоторый теоретико-познавательный недостаток, который, пожалуй, впервые был ясно отмечен Эрнстом Махом. Мы поясним его суть на следующем примере. Пусть два жидких тела одинаковой величины и состава свободно парят в пространстве на таком большом расстоянии друг от друга (и от всех прочих масс), что должны приниматься во внимание только те гравитационные силы, с которыми действуют друг на друга части одного и того же тела. Пусть расстояние между этими телами остается постоянным. Кроме того, будем считать, что не происходит перемещения друг относительно друга частей одного и того же тела. При этом пусть каждая масса, рассматриваемая наблюдателем, покоящимся относительно другой массы, вращается вокруг линии, соединяющей массы с постоянной угловой скоростью (это относительное движение обеих масс всегда возможно установить). Наконец, представим себе, что поверхности обоих тел (S1 и S2) измерены с помощью масштабов (покоящихся относительно этих тел). Будем считать, что согласно результатам измерений поверхность S1 представляет собой сферу, а поверхность S2 – эллипсоид вращения. Далее возникает вопрос: по какой причине тела S1 и S2 ведут себя по-разному? Ответ на этот вопрос может быть признан удовлетворительным с теоретико-познавательной точки зрения только тогда, когда обстоятельство, указанное в качестве причины, является наблюдаемым опытным фактом. Дело в том, что принцип причинности только тогда имеет смысл суждения о явлениях в мире опыта, когда в качестве причин и следствий в конечном итоге оказываются лишь собственно наблюдаемые факты.
Механика Ньютона не дает удовлетворительного ответа на поставленный выше вопрос, а говорит следующее. Законы механики справедливы для пространства R1, относительно которого тело S1 находится в покое, но несправедливы для пространства R2, относительно которого находится в покое тело S2. Однако вводимое при этом галилеево пространство R1 (и движение по отношению к этому пространству), по сути, является фиктивной причиной, а вовсе не наблюдаемым фактом. Другими словами, очевидно, что механика Ньютона в рассматриваемом случае удовлетворяет требованию причинности не по существу, но лишь кажущимся образом, возлагая ответственность за наблюдаемое различное поведение тел S1 и S2 на фиктивную причину – пространство R1.
Удовлетворительным ответом на рассматриваемый вопрос может быть только такой: физическая система, состоящая из тел S1 и S2, сама по себе не дает возможности указать причину, с помощью которой можно было бы объяснить различное поведение тел S1 и S2. Следовательно, причина должна лежать вне этой системы. Из последнего утверждения, в свою очередь, следует вывод, что общие законы движения, которые, в частности, определяют форму тел S1 и S2, должны быть таковы, чтобы механические свойства тел S1 и S2 в значительной степени обусловливались отдаленными массами, которые мы не включили в рассматриваемую систему. Эти отдаленные массы (и их относительные движения по отношению к рассматриваемым телам) должны тогда рассматриваться как носители принципиально наблюдаемых причин различного поведения рассматриваемых тел S1 и S2, и они становятся на место фиктивной причины R1. Из всех возможных пространств R1, R2 и т. д., движущихся любым образом относительно друг друга, ни одному из них не должно изначально отдаваться предпочтение, если только мы хотим устранить указанный теоретико-познавательный недостаток. Законы физики должны быть составлены так, чтобы они были справедливы для произвольно движущихся координатных систем. Таким образом мы приходим к расширению постулата относительности.
Помимо рассмотренного важнейшего теоретико-познавательного аргумента, в пользу расширения теории относительности свидетельствует и еще один хорошо известный физический факт. Пусть К – галилеева координатная система, т. е. такая, относительно которой (по крайней мере, в рассматриваемой четырехмерной области) некоторая масса, достаточно удаленная от других, движется прямолинейно и равномерно. Пусть К’ – вторая координатная система, которая относительно К движется равномерно ускоренно. Тогда достаточно изолированная от других масса совершает относительно К’ ускоренное движение, причем ни ускорение, ни направление этого ускорения не зависят от химического состава и физического состояния этой массы.
Может ли наблюдатель, который находится в состоянии покоя относительно координатной системы К’, из всего вышесказанного заключить, что он находится в «действительно» ускоренной, координатной системе? Ответ на этот вопрос должен быть отрицательным, потому что только что указанное поведение масс, свободно движущихся относительно К’, может быть столь же хорошо объяснено и другим, следующим образом. Координатная система К’ не обладает ускорением, однако в рассматриваемой пространственно-временной области имеется гравитационное поле, которое и вызывает ускоренное движение тел относительно системы К’. Объяснение такого рода становится возможным благодаря тому, что из опыта нам известно о существовании силового поля (а именно: гравитационного поля), обладающего замечательным свойством сообщать всем телам одно и то же ускорение. Механическое поведение тел относительно координатной системы К’ будет таким же, какое обнаруживается на опыте по отношению к системам, которые мы привыкли рассматривать как «покоящиеся» или как «законные»; поэтому и с физической точки зрения естественно считать, что обе системы К’ и К с одинаковым правом могут рассматриваться как «покоящиеся». Другими словами, обе системы равноправны в качестве координатных систем для физического описания процессов.

Теория относительности опирается на постоянство скорости света (300 000 километров в секунду). За год свет проходит около 10 триллионов километров. Это расстояние называется световым годом. Он равен 63 241 астрономической единице (1 а. е. – это расстояние от Земли до Солнца). От нас до Плутона 49,3 астрономической единицы, а до ближайшей звезды – Альфа Центавра – 4,3 светового года. До границы нашей галактики Млечный Путь – 50 тысяч световых лет, а до ближайшей галактики Андромеды – 2,3 миллиона световых лет. Большинство звезд, которые видно невооруженным глазом, находятся от нас в пределах 1000 световых лет.
Из указанных соображений становится ясно, что построение общей теории относительности должно одновременно привести и к построению теории тяготения, потому что гравитационное поле можно «создать» простым изменением координатной системы. Кроме того, очевидно, что принцип постоянства скорости света в пустоте должен быть изменен, ибо легко убедиться в том, что траектория луча света относительно системы К’ в общем случае должна быть кривой, если свет относительно системы К распространяется прямолинейно и с определенной постоянной скоростью.
§ 3. Пространственно-временной континуум. Требование общей ковариантности уравнений, выражающих общие законы природы
Так же как и в специальной теории относительности, в классической механике пространственные и временные координаты содержат непосредственный физический смысл. Когда говорят, что точечное событие имеет координату x1, то это означает следующее. Построенную по правилам евклидовой геометрии при помощи твердых стержней проекцию точечного события на ось X1 получают, откладывая определенную линейку – единичный масштаб – х1 раз от начала координат по направлению оси X1. Когда говорят, что точка имеет координату х4 = t, то это означает, что по часам (некоторому эталону времени), покоящимся относительно координатной системы, пространственно (практически) совпадающим с точечным событием и выверенным по определенным правилам, прошло х4 = t периодов, когда наступило точечное событие10.
Такое понимание пространства и времени всегда представлялось взору физиков, хотя, быть может, большей частью и бессознательно. Это ясно видно из той роли, какую играют эти понятия в физических измерениях. Такое толкование читатель должен был положить также в основу второго рассуждения последнего параграфа для того, чтобы придать ему некоторый смысл. Однако мы покажем теперь, что это толкование нужно отбросить и заменить более общим, чтобы последовательно провести общий постулат относительности, при условии, что специальная теория относительности сохраняется в предельном случае отсутствия гравитационного поля.
Введем в пространстве, свободном от гравитационных полей, галилееву координатную систему К(х, у, z, t) и, кроме того, координатную систему К’(х’, у’, z’, t’), которая равномерно вращается относительно К. Пусть начала координат обеих систем, так же как и их оси Z, все время совпадают друг с другом. Покажем, что вышеприведенные определения, касающиеся физического смысла длин и времен, не пригодны для изучения пространства и времени в системе К’.
Из соображений симметрии очевидно, что окружность в координатной плоскости XY системы К с центром в начале координат может в то же время рассматриваться как окружность в координатной плоскости X’Y’ системы К’. Теперь представим себе, что длина и диаметр этой окружности измерены при помощи единичного масштаба (бесконечно малого по сравнению с радиусом) и затем взято отношение обоих результатов измерения. Если выполнить этот эксперимент с масштабом, покоящимся относительно галилеевой системы К, то в качестве частного получится число π. Результатом измерения, выполненного с масштабом, покоящимся относительно системы К’, будет число большее π. В этом легко убедиться, если судить о процессе измерения из «покоящейся» системы К и принять во внимание, что масштаб, приложенный по касательной к окружности, претерпевает лоренцево сокращение, а радиально приложенный масштаб не изменяется. Поэтому относительно системы К’ геометрия Евклида оказывается несправедливой. Установленное нами ранее представление о координатах, которое предполагает применимость евклидовой геометрии, оказывается непригодным в системе К’. Также невозможным оказывается и введение в К’ удовлетворяющего физическим требованиям времени, которое показывали бы одинаковые часы, покоящиеся относительно К’. Для того чтобы в этом убедиться, представим себе, что в начале координат и где-нибудь на окружности установлено двое одинаковых часов, наблюдаемых из «покоящейся» системы К. Далее, согласно известному выводу специальной теории относительности, наблюдение по часам в системе К дает, что часы, установленные на окружности, идут медленнее часов, которые помещены в начале координат, поскольку первые движутся, а последние нет. Наблюдатель, который находится в общем начале координат и который способен, пользуясь светом, наблюдать часы, находящиеся на окружности, обнаружит, что часы, установленные на окружности, идут медленнее, чем часы, установленные рядом с ним. Поскольку наблюдатель не решится считать скорость света на пройденном светом пути явной функцией времени, то он объяснит свое наблюдение тем, что часы на окружности «действительно» идут медленнее часов, установленных в начале координат. Таким образом, он будет вынужден дать времени такое определение, которое указывало бы, что скорость хода часов зависит от места.

Три модели будущего Вселенной: инфляция, расширение, сжатие.
ВВЕРХУ
Вселенная вверху пережила период внезапного расширения, но затем начала схлопываться, что в конце концов приведет к Большому сжатию в массивную черную дыру.
В СЕРЕДИНЕ
Вселенная, подобная нашей: в ней наблюдается второе расширение с ускорением, которое может продолжаться, пока вселенная не превратится в холодную безжизненную пустоту или, как в предыдущем случае, не образует черную дыру.
ВНИЗУ
Вселенная, которая начинает расширяться на самых первых этапах существования и продолжает этот процесс, так и не создав ни галактик, ни звезд. Оранжевый круг на каждой иллюстрации отмечает момент, когда происходит основное расширение с ускорением.
Итак, мы приходим к следующему выводу: в общей теории относительности пространственные и временные величины не могут быть определены так, чтобы разности пространственных координат могли быть измерены непосредственно единичным масштабом, а разности временных – посредством стандартных часов.
Прежний способ, заключавшийся в определенном построении системы координат в пространственно-временном континууме, оказывается неприменимым. Представляется, что не существует пути, который позволил бы приспособить к четырехмерному миру такие координатные системы, чтобы с помощью их можно было бы ожидать особенно простой формулировки законов природы. Не остается ничего другого, как признать все мыслимые координатные системы принципиально равноправными для описания природы. Последнее равносильно следующему требованию.
Общие законы природы должны быть выражены через уравнения, справедливые во всех координатных системах, т. е. эти уравнения должны быть ковариантными относительно любых подстановок (общековариантными).
Физика, удовлетворяющая этому постулату, удовлетворит и общему постулату относительности, потому что в совокупности всех подстановок найдутся такие, которые соответствуют всем относительным движениям (трехмерных) координатных систем. Тот факт, что это требование общей ковариантности, отнимающее у пространства и времени последний остаток физической предметности, является естественным, видно из следующего соображения. Все наши пространственно-временные констатации всегда сводятся к установлению пространственно-временных совпадений. Так, если события состояли только в движении материальных точек, то в конце концов наблюдались бы только встречи двух или нескольких таких точек. Результаты наших измерений также являются не чем иным, как констатацией подобных встреч между материальными точками наших масштабов с другими материальными точками и соответственно совпадений между часовыми стрелками, точками циферблата и рассматриваемыми точечными событиями, происходящими в том же месте и в то же время.
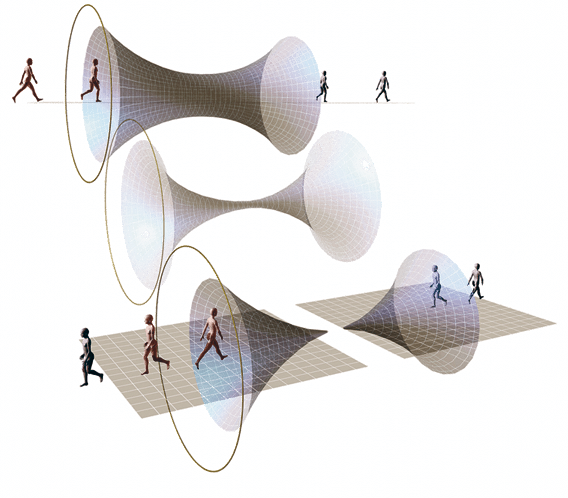
Кротовые норы соединяют разные области пространства и времени. Теоретически они опасны тем, что открываются совсем ненадолго, а затем закрываются, отрезав путь назад.
Координатная система вводится только для более простого описания совокупности совпадений. Четыре пространственно-временные переменные х1, х2, х3, х4 сопоставляются с миром таким образом, чтобы каждому точечному событию соответствовала некоторая система значений переменных х1, … х4. Двум совпадающим точечным событиям соответствует одна и та же система значений переменных х1, … х4, т. е. совпадение характеризуется равенством координат. Вводя вместо переменных х1, … х4 любые четыре функции от х’1, … х’4 как новую координатную систему так, чтобы эти системы значений однозначно соответствовали друг другу, мы получим, что равенство соответствующих координат в новой системе тоже является выражением пространственно-временного совпадения двух точечных событий. Так как все наши физические опытные данные можно в конце концов свести к таким совпадениям, то мы не можем априори отдать предпочтение какой-то выборочной координатной системе перед всеми другими. Таким образом, мы приходим к требованию общей ковариантности.

Парадокс кротовых нор наталкивает на мысль, что если мы вернемся в прошлое, то сумеем изменить его, а следовательно, изменится и будущее. Что будет, если вернуться в прошлое и убить собственного деда до того, как он успеет зачать твоего отца или мать?

