Книга: На плечах гигантов
Назад: Основы общей теории относительности А. Принципиальные соображения о постулате относительности
Дальше: Стивен Хокинг
Вопросы космологии и общая теория относительности
Дифференциальное уравнение Пуассона имеет вид
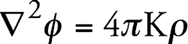
(1)
В совокупности с уравнением движения материальной точки это уравнение не может полностью заменить теорию дальнодействия Ньютона. К ним необходимо добавить условие того, что потенциал φ в пространственной бесконечности стремится к определенному пределу. Схожим образом обстоит дело и в теории тяготения, которая следует из общего принципа относительности. Здесь также к дифференциальным уравнениям должны быть добавлены граничные условия на пространственной бесконечности, если мы на самом деле рассматриваем мир бесконечно протяженным в пространстве.
В задачах, связанных с планетной системой, выбираются эти граничные условия при допущении, что можно выбрать такую координатную систему, в которой все потенциалы тяготения gμν на пространственной бесконечности становятся постоянными. Но изначально совершенно не очевидно, что при рассмотрении более значительных областей Вселенной можно вводить те же самые граничные условия. Ниже изложим соображения, которые мы получили до настоящего времени по этому принципиально важному вопросу.
§ 1. Теория Ньютона
Граничное условие Ньютона в форме существования постоянного предела для φ в пространственной бесконечности ведет к тому, что плотность материи на бесконечности обращается в нуль. Действительно, пусть во Вселенной существует область, вокруг которой гравитационное поле материи, рассматриваемое в целом, обладает сферической симметрией (центр). Тогда из уравнения Пуассона следует, что средняя плотность ρ с увеличением расстояния r от центра должна стремиться к нулю быстрее, чем 1/r2, для того чтобы φ на бесконечности стремилось к некоторому пределу. В этом смысле мир по Ньютону конечен, хотя может обладать бесконечно большой общей массой.
Из приведенного рассуждения прежде всего следует, что излучение, испускаемое небесными телами, частично покинет мир Ньютона по радиальному от центра направлению с тем, чтобы бесследно затеряться на бесконечности. Не может ли произойти то же с целым небесным телом? Едва ли можно отрицать этот факт, поскольку из предположения о существовании конечного предела для φ в пространственной бесконечности следует, что обладающее конечной кинетической энергией небесное тело может достичь пространственной бесконечности, преодолев ньютоновские силы притяжения. Согласно статистической механике, такие события должны происходить до тех пор, пока общая энергия звездной системы достаточно велика, чтобы – при переносе ее на одно небесное тело – последнее могло совершить путешествие на бесконечность, откуда оно никогда не сможет вернуться.
Можно было бы попытаться обойти эту своеобразную трудность, допустив, что указанный граничный потенциал имеет на бесконечности очень большое значение. Это было бы приемлемо, если бы изменение потенциала тяготения не определялось самим небесным телом. В действительности мы с неизбежностью приходим к заключению, что наличие значительных разностей потенциалов гравитационного поля противоречит фактам. Наоборот, разности потенциалов должны быть такого малого порядка, чтобы определяемые ими скорости звезд не превосходили фактически наблюдаемых скоростей.
Закон Больцмана распределения молекул газа, примененный к звездам, рассматривающий звездную систему как газ, который находится в стационарном тепловом движении, приводит к тому, что ньютоновская Вселенная вообще не могла бы существовать. Это следует из того, что конечной разности потенциалов между центром и бесконечностью соответствует конечное отношение плотностей. Таким образом, нулевая плотность на бесконечности влечет за собой нулевую плотность в центре.
Эти трудности, по-видимому, нельзя преодолеть, оставаясь в рамках теории Ньютона. Возникает вопрос, нельзя ли преодолеть их путем модификации теории Ньютона. Для этого прежде всего укажем путь, который не следует принимать слишком серьезно, так как он служит только для того, чтобы лучше уяснить последующие рассуждения. Вместо уравнения Пуассона напишем
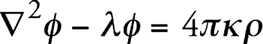
(2)
где λ представляет собой некоторую универсальную постоянную.
Если ρ0 есть постоянная плотность распределения массы, то
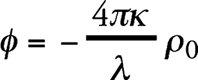
(3)
есть решение уравнения (2). Оно соответствует случаю равномерного пространственного распределения неподвижных звезд, причем плотность ρ0 может равняться действительной средней плотности материи в мировом пространстве. Это решение соответствует бесконечно протяженному пространству, в среднем равномерно заполненному материей.
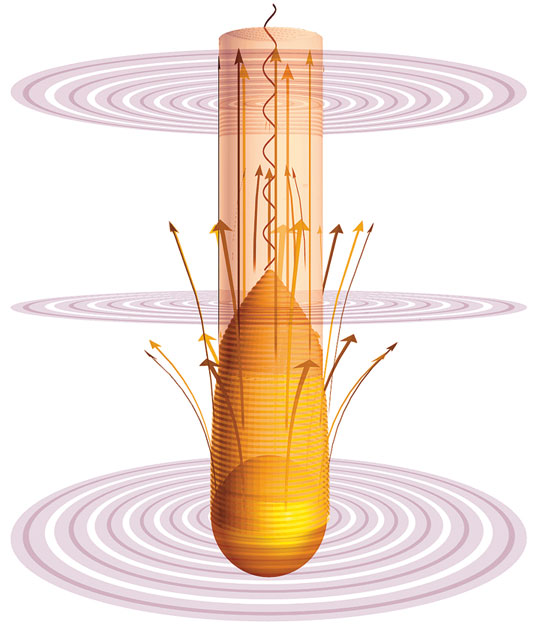
Звезда на стабильной стадии существования. Показано, что с ее поверхности исходит свет.
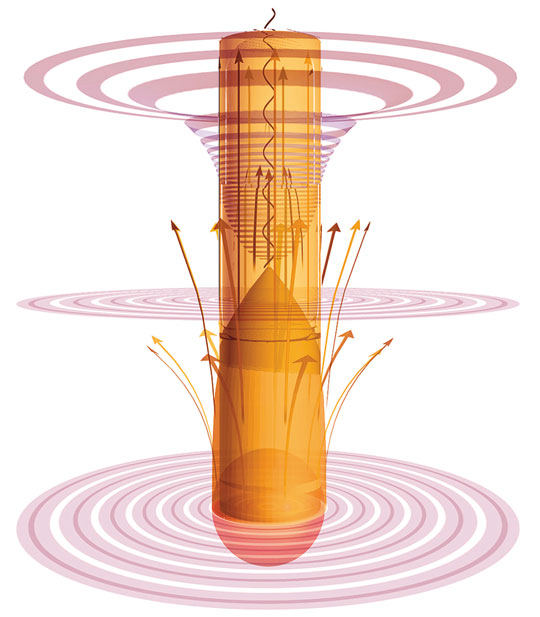
Звезда начинает схлопываться (средняя стадия), ее свет стягивается обратно к поверхности, пока не возникает граница (горизонт событий), за которую свет уже не может вырваться.
Если теперь предположить, что имеются местные неравномерности в распределении материи, не изменяющие среднего значения плотности распределения, то к постоянному значению (3) потенциала φ придется добавить дополнительную величину φ, которая вблизи более плотных масс будет тем более похожа на поле Ньютона, чем меньше αφ по сравнению с 4πΚρ.
Такой мир не имел бы центра по отношению к гравитационному полю, и не было бы надобности допускать, что плотность уменьшается на бесконечности. Наоборот, и средний потенциал, и средняя плотность были бы постоянны вплоть до бесконечности. При этом конфликт, отмеченный между теорией Ньютона и статистической механикой, отсутствовал бы. При постоянной (крайне малой) плотности материя находится в равновесии, не требуя внутренних сил (давления) для поддержания этого равновесия.
§ 2. Граничные условия, требуемые общей теорией относительности
В дальнейшем я предлагаю читателю последовать по пройденному мной самим извилистому и неровному пути, поскольку, как мне кажется, только так будет интересен конечный результат. Я пришел к убеждению, что уравнения гравитационного поля, которых я до сих пор придерживался, нуждаются еще в некоторой модификации, чтобы можно было на базе общей теории относительности избежать тех принципиальных трудностей, которые в предыдущем параграфе были указаны для теории Ньютона. Эта модификация полностью соответствует переходу от уравнения Пуассона (1) к уравнению (2) предыдущего параграфа. Тогда, наконец, получается, что граничные условия на пространственной бесконечности вообще отпадают, поскольку мировой континуум должен в отношении своих пространственных размеров рассматриваться как замкнутый континуум, имеющий конечный пространственный (трехмерный) объем.
Высказанное мной недавно мнение относительно граничных условий на пространственной бесконечности основано на следующих соображениях. В последовательной теории относительности нельзя определять инерцию по отношению к «пространству», но можно определять инерцию масс относительно друг друга. Следовательно, если я удаляю какую-нибудь массу на достаточно большое расстояние от всех других масс Вселенной, то инерция этой массы должна стремиться к нулю. Попытаемся сформулировать это условие математически.
Согласно общей теории относительности, импульс (с обратным знаком) определяется первыми тремя компонентами, а энергия – последней компонентой умноженного на √-g ковариантного тензора
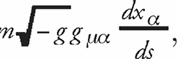
(4)
причем, как всегда,
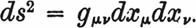
(5)
В особенно наглядном случае, когда координатную систему можно выбрать так, чтобы гравитационное поле в каждой точке было пространственно изотропно, последняя величина принимает более простой вид
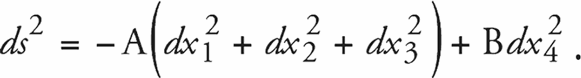
Если одновременно
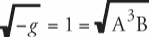
то в случае малых скоростей из выражения (4) для компонент импульса в первом приближении имеем
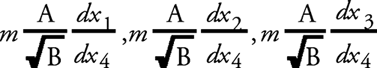
и для энергии (в случае покоя)
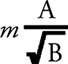
Из выражений для импульса следует, что играет роль инертной массы. Так как m – константа, связанная с точечной массой и независящая от положения этой массы, то при соблюдении условия, установленного для определителя, это выражение на пространственной бесконечности обращается в нуль только тогда, когда А стремится к нулю, а В стремится к бесконечности.
Рассмотренное поведение метрических коэффициентов gμν представляется нам как бы следствием относительности всякой инерции. Отсюда следует также и тот факт, что потенциальная энергия m√B точки на бесконечности становится бесконечно большой. Точечная масса никогда не может покинуть систему. Более детальное исследование показывает, что то же самое справедливо и для лучей света. Вселенная при таком поведении потенциала гравитационного поля на бесконечности не подвергалась бы опасности стать пустой, на что указывалось при обсуждении ньютоновской теории.
Упрощенные допущения о гравитационном потенциале, которые лежат в основе этих рассуждений, введены только для большей наглядности. Для описания поведения gμν на бесконечности можно найти общую формулировку, которая выразит суть без всяких ограничивающих допущений.
Пользуясь дружеской помощью математика Громмера, я исследовал центрально-симметричное статическое гравитационное поле, которое выражается на бесконечности указанным образом. Из заданного потенциала гравитационного поля gμν на основе уравнений гравитационного поля был вычислен тензор Tμν энергии материи. Однако при этом оказалось, что для звездной системы подобного рода граничные условия никак не могут быть приняты. Недавно это вполне справедливо было отмечено также астрономом де Ситтером. Действительно, контравариантный тензор Tμ энергии весомой материи имеет вид
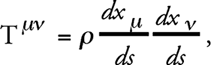
где ρ означает естественно измеренную плотность материи.
При надлежащем выборе координатной системы скорости звезд очень малы по сравнению со скоростью света. Поэтому ds можно заменить на 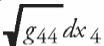 . Таким образом, все компоненты тензора Tμν очень малы по сравнению с последней его компонентой, T44. Однако это условие никак нельзя совместить с выбранными граничными условиями. После всего изложенного такой результат не вызывает удивления. Факт незначительности звездных скоростей позволяет заключить, что всюду, где имеются неподвижные звезды, потенциал гравитационного поля (в нашем случае √В) не может быть существенно больше, чем у нас. Последнее следует из статистических соображений так же, как и в теории Ньютона. Во всяком случае, наши вычисления привели меня к убеждению, что подобные условия вырождения для gμν в пространственной бесконечности не могут быть постулированы.
. Таким образом, все компоненты тензора Tμν очень малы по сравнению с последней его компонентой, T44. Однако это условие никак нельзя совместить с выбранными граничными условиями. После всего изложенного такой результат не вызывает удивления. Факт незначительности звездных скоростей позволяет заключить, что всюду, где имеются неподвижные звезды, потенциал гравитационного поля (в нашем случае √В) не может быть существенно больше, чем у нас. Последнее следует из статистических соображений так же, как и в теории Ньютона. Во всяком случае, наши вычисления привели меня к убеждению, что подобные условия вырождения для gμν в пространственной бесконечности не могут быть постулированы.
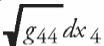 . Таким образом, все компоненты тензора Tμν очень малы по сравнению с последней его компонентой, T44. Однако это условие никак нельзя совместить с выбранными граничными условиями. После всего изложенного такой результат не вызывает удивления. Факт незначительности звездных скоростей позволяет заключить, что всюду, где имеются неподвижные звезды, потенциал гравитационного поля (в нашем случае √В) не может быть существенно больше, чем у нас. Последнее следует из статистических соображений так же, как и в теории Ньютона. Во всяком случае, наши вычисления привели меня к убеждению, что подобные условия вырождения для gμν в пространственной бесконечности не могут быть постулированы.
. Таким образом, все компоненты тензора Tμν очень малы по сравнению с последней его компонентой, T44. Однако это условие никак нельзя совместить с выбранными граничными условиями. После всего изложенного такой результат не вызывает удивления. Факт незначительности звездных скоростей позволяет заключить, что всюду, где имеются неподвижные звезды, потенциал гравитационного поля (в нашем случае √В) не может быть существенно больше, чем у нас. Последнее следует из статистических соображений так же, как и в теории Ньютона. Во всяком случае, наши вычисления привели меня к убеждению, что подобные условия вырождения для gμν в пространственной бесконечности не могут быть постулированы.Неудача этой попытки указывает на две возможности: а) требовать, как в случае планетной проблемы, чтобы на пространственной бесконечности gμν при надлежащем выборе системы координат стремились к значениям

или б) не устанавливать для пространственной бесконечности никаких фиксированных граничных условий. В каждом отдельном случае следует особо задавать gμν на пространственной границе рассматриваемой области так же, как мы привыкли это делать до сих пор, задавая начальные условия.
Возможность «б» не соответствует какому-либо решению проблемы. Она означает отказ от ее решения. Правомерность такой точки зрения нельзя отрицать – в настоящее время ее придерживается де Ситтер. Но я должен признаться, что мне трудно было бы пойти на столь большие уступки в этом принципиальном вопросе. С этим я соглашусь только в том случае, если все усилия найти удовлетворительные граничные условия окажутся тщетными.
Возможность «а» неудовлетворительна во многих отношениях. Во-первых, такие граничные условия предполагают определенный выбор системы отсчета, что несовместимо с духом принципа относительности. Во-вторых, эта возможность ведет к отказу от требования относительности инерции. Действительно, инерция материальной точки с естественно измеренной массой m зависит от gμν, но последние лишь очень мало отличаются от постулированных значений на пространственной бесконечности. Благодаря этому, несмотря на то что материя (находящаяся на конечном расстоянии) влияет на инерцию, но все-таки не обусловливает последнюю. Если бы существовала только одна материальная точка, то она, согласно этому представлению, обладала бы почти такой же инерцией, как и в том случае, когда она окружена всеми прочими массами нашего реального мира. Наконец, против этого представления нужно выдвинуть те же статистические возражения, которые выше были указаны для теории Ньютона.

Теория струн, разработанная по большей части уже после смерти Эйнштейна, породила новые модели зарождения Вселенной.
Из всего сказанного выше следует, что мне не удалось установить граничных условий для пространственной бесконечности. Тем не менее существует еще одна возможность, позволяющая обойтись без отказа, упомянутого в «б». Так, если бы можно было рассматривать мир в его пространственной протяженности как замкнутый континуум, то полностью отпала бы необходимость в подобного рода граничных условиях. Из дальнейшего будет видно, что и требование общего принципа относительности, и факт незначительности скоростей звезд совместимы с гипотезой пространственной замкнутости Вселенной. Однако для осуществления этого необходимо некоторое обобщение уравнений гравитационного поля.
§ 3. Пространственно замкнутый мир с равномерно распределенной материей
Согласно общей теории относительности, метрический характер (кривизна) четырехмерного пространственно-временного континуума определяется в каждой точке находящейся в ней материей и состоянием последней. Из-за неравномерности распределения материи метрическая структура этого континуума должна быть крайне запутанной. Однако говоря о структуре пространства в целом, можно представить материю как бы равномерно распределенной по очень большой области пространства, так что ее плотность распределения становится чрезвычайно медленно меняющейся функцией. В данном случае мы поступаем так же, как геодезисты, которые крайне сложную в деталях поверхность Земли приближенно заменяют эллипсоидом.
Наиболее важное из того, что нам дает опыт о распределении материи, заключается в том, что относительные скорости звезд очень малы по сравнению со скоростью света. На этом основании я полагаю, что на начальном этапе в основу наших рассуждений можно положить приближенное допущение: пусть существует координатная система, относительно которой материю можно рассматривать находящейся в течение продолжительного времени в покое. По отношению к этой координатной системе контравариантный тензор материи Tμν, в силу (5), имеет следующий простой вид:

(6)
Скаляр ρ (средней) плотности распределения изначально может быть зависимым от пространственных координат, но, предположив, что мир пространственно замкнут, мы можем сформулировать гипотезу о том, что ρ не зависит от места. Эту гипотезу мы положим в основу дальнейших рассуждений.
Что касается гравитационного поля, то из уравнения движения материальной точки
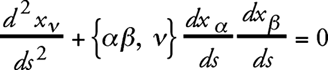
следует, что материальная точка в статическом гравитационном поле может находиться в покое только тогда, когда g44 не зависит от места. Так как, кроме того, мы для всех величин предполагаем независимость от временной координаты х4, то для искомого решения можем потребовать, чтобы для всех xν
g44 = 1. (7)
Далее, как это обычно делается в статических задачах, примем, что
g14 = g24= g34= 0. (8)
Остается определить те компоненты потенциала гравитационного поля, которые характеризуют чисто пространственно-геометрические свойства нашего континуума (g11, g12, …, g33). Из введенного допущения о равномерности распределения масс, создающих поле, следует, что и кривизна искомого метрического пространства должна быть постоянной. Таким образом, при заданном распределении масс искомый замкнутый континуум (х1, х2, х3 при постоянном х4) должен быть сферическим пространством.
Такое пространство можно получить, например, если исходить из евклидова пространства (ξ1, ξ2, ξ3, ξ4) четырех измерений с линейным элементом dσ. В этом случае
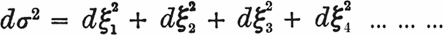
(9)
Рассмотрим в этом пространстве гиперповерхность
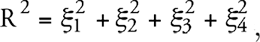
(10)
где R – постоянная. Точки этой гиперповерхности образуют трехмерный континуум – сферический объем с радиусом кривизны R.
Четырехмерное евклидово пространство, из которого мы исходили, служит только для удобного определения нашей гиперповерхности. Нас интересуют только точки этой поверхности, метрические свойства которой должны совпадать со свойствами физического пространства с равномерным распределением материи. Для описания этого трехмерного континуума воспользуемся координатами ξ1, ξ2, ξ3 (проекции на гиперплоскость ξ4 = 0), так как, в силу (10), можно ξ4 выразить через ξ1, ξ2, ξ3. Исключая ξ4 из (9), получаем следующее выражение для линейного элемента сферического пространства:
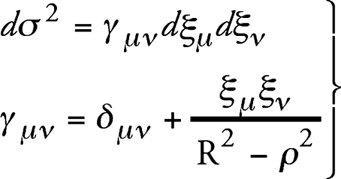
где δμν = 1, если μ = ν, и δμν = 0, если μ =/ ν,
.
Выбранные координаты удобны, когда речь идет об исследовании окрестности точки ξ1 = ξ2 = ξ3 = 0.
Итак, теперь у нас есть также и линейный элемент искомого четырехмерного пространственно-временного мира. Очевидно, для потенциалов gμν, у которых оба индекса отличаются от 4, мы должны написать
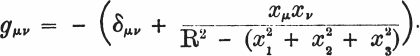
(12)
Полученное равенство вместе с соотношениями (7) и (8) вполне определяет свойства масштабов, часов и лучей света в рассматриваемом четырехмерном мире.
§ 4. Заключительные замечания
Приведенные выше рассуждения показывают, что теоретически можно построить материю только из гравитационного и электромагнитного полей, не вводя никаких гипотетических дополнительных членов в духе теории Ми. Эта возможность представляется особенно содержательной потому, что она освобождает нас от необходимости введения особой постоянной α для решения космологической проблемы. С другой стороны, присутствует и своеобразная трудность. Так, если применить уравнение (1) к случаю статического сферически симметричного поля, то мы получаем на одно уравнение меньше, чем нужно для определения gμν и Φμν. Таким образом оказывается, что всякое распределение электричества, совместимое со сферической симметрией, может оставаться в равновесии. В настоящий момент проблему построения теории элементарных частиц нельзя решить на основе указанных уравнений поля.
Назад: Основы общей теории относительности А. Принципиальные соображения о постулате относительности
Дальше: Стивен Хокинг

