Пусть имеется координатная система, в которой справедливы уравнения механики Ньютона. С целью отличить эту координатную систему от вводимых позже координатных систем и для уточнения терминологии назовем ее «покоящейся системой».

Если относительно покоящейся системы некоторая материальная точка находится в покое, то положение этой точки относительно такой координатной системы может быть определено методами евклидовой геометрии с помощью твердых масштабов и выражено в декартовых координатах.

Если мы хотим дать описание движения какой-нибудь материальной точки, то мы задаем значения ее координат как функций времени. При этом нужно иметь в виду, что такое математическое описание имеет физический смысл только тогда, когда предварительно установлено, что подразумевается под «временем». Другими словами, необходимо обратить внимание на то, что все наши выводы, в которых как-то задействовано время, всегда являются выводами об одновременных событиях. Если я, например, говорю: «Этот поезд прибывает сюда в 7 часов», – то это означает примерно следующее: «Указание маленькой стрелки моих часов на 7 часов и прибытие поезда суть одновременные события».

На первый взгляд может показаться, что все трудности определения «времени» могут быть преодолены, если вместо слова «время» написать «положение маленькой стрелки моих часов». Такое определение, действительно, достаточно в том случае, когда речь идет об определении времени только для того самого места, в котором как раз находятся часы. Однако такого определения уже недостаточно, как только речь пойдет о связи друг с другом во времени ряда событий, протекающих в различных местах. Или, что то же самое, когда речь пойдет об установлении времени для тех событий, которые происходят в местах, удаленных от часов.

Для того чтобы определить время событий, мы могли бы, конечно, удовлетвориться тем, что заставили бы некоторого наблюдателя, находящегося с часами в начале координат, сопоставлять соответствующее положение стрелки часов с каждым световым сигналом, идущим к нему через пустоту и дающим знать о регистрируемом событии. Однако такое сопоставление связано с тем неудобством, известным нам из опыта, что оно не будет независимым от местонахождения наблюдателя, снабженного часами. Мы придем к гораздо более практическому определению путем следующих рассуждений.

Поместим часы в точке А пространства. Тогда наблюдатель, находящийся в А, может устанавливать время событий в малой окрестности А, наблюдая одновременные с этими событиями положения стрелок часов. Если в другой точке В пространства также имеются часы (мы добавим: точно такие же часы, как в точке А), то в малой окрестности В также возможна временная оценка событий находящимся в В наблюдателем. Однако невозможно без дальнейших предположений сравнивать во времени какое-либо событие в А с событием в В, потому что мы определили пока только «А-время» и «В-время», но не общее для А и В «время». Последнее можно установить, вводя определение, что «время», необходимое для прохождения света из А в В, равно «времени», требуемому для прохождения света из В в А. Пусть в момент t_A по «А-времени» луч света выходит из А в В, отражается в момент t_B по «B-времени» от В к А и возвращается назад в А в момент t’_A по «А-времени». Часы в А и В будут идти, согласно определению, синхронно, если

Допустим, что данное определение синхронности можно дать однозначным образом и, кроме того, для сколь угодно большого числа точек и что, таким образом, справедливы следующие утверждения:

1) если часы в В идут синхронно с часами в А, то часы в А идут синхронно с часами в В;

2) если часы в А идут синхронно как с часами в В, так и с часами в С, то часы в В и С также идут синхронно относительно друг друга.

Таким образом, пользуясь некоторыми (мысленными) физическими экспериментами, мы установили, что нужно понимать под синхронно идущими, находящимися в различных местах покоящимися часами, и благодаря этому, очевидно, достигли определения понятий: «одновременность» и «время». «Время» события – это одновременное с событием показание покоящихся часов, которые находятся в месте события и которые идут синхронно с некоторыми определенными покоящимися часами, причем с одними и теми же часами при всех определениях времени.

Согласно опыту, будем также считать, что величина есть универсальная постоянная (скорость света в пустоте).

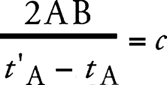
Существенным является то, что мы определили время с помощью покоящихся часов в покоящейся системе. Такое время, принадлежащее к покоящейся системе, будем называть «временем покоящейся системы».

Последующие соображения опираются на принцип относительности и на принцип постоянства скорости света. Мы формулируем оба принципа следующим образом.

1. Законы, по которым изменяются состояния физических систем, не зависят от того, к которой из двух координатных систем, движущихся относительно друг друга равномерно и прямолинейно, эти изменения состояния относятся.

2. Каждый луч света движется в «покоящейся» системе координат с определенной скоростью V, независимо от того, испускается ли этот луч света покоящимся или движущимся телом.

При этом

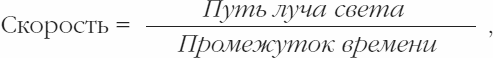
причем «промежуток времени» следует понимать в смысле определения в § 1.

Рассмотрим покоящийся твердый стержень, и пусть его длина, измеренная также покоящимся масштабом, есть l. Пусть теперь стержню, ось которого направлена по оси X покоящейся координатной системы, сообщается равномерное и параллельное оси X поступательное движение (со скоростью v) в сторону возрастающих значений х. Поставим теперь вопрос о длине движущегося стержня, которую мы полагаем определенной с помощью следующих двух операций:

а) наблюдатель движется вместе с данным масштабом и с измеряемым стержнем и измеряет длину стержня непосредственно путем прикладывания масштаба так же, как если бы измеряемый стержень, наблюдатель и масштаб находились в покое;

б) наблюдатель устанавливает с помощью расставленных в покоящейся системе синхронных (в смысле § 1) покоящихся часов, в каких точках покоящейся системы расположены начало и конец измеряемого стержня в некоторый определенный момент времени t. Расстояние между этими двумя точками, измеренное использованным выше, но уже покоящимся масштабом, есть длина, которую можно обозначить как «длину стержня».

Согласно принципу относительности, длина, определяемая операцией «а», которую мы будем называть «длиной стержня в движущейся системе», должна равняться длине l покоящегося стержня.

Длину, устанавливаемую операцией «б», которую мы будем называть «длиной (движущегося) стержня в покоящейся системе», мы определим, основываясь на наших двух принципах, и найдем, что она отлична от l.

В обычно применяемой кинематике постулируется, что длины, определенные с помощью двух упомянутых операций, равны друг другу, или, другими словами, что движущееся твердое тело в момент времени t в геометрическом отношении вполне может быть заменено тем же телом, когда оно покоится в определенном положении.

Пусть теперь к обоим концам стержня (А и В) прикрепляются часы, синхронные с часами покоящейся системы. Другими словами, показания этих часов соответствуют «времени покоящейся системы» в тех местах, в которых эти часы как раз находятся; следовательно, эти часы «синхронны в покоящейся системе».

Далее, представим себе, что у каждых часов расположен движущийся вместе с ними наблюдатель, и пусть эти наблюдатели применяют к обоим часам установленный в § 1 критерий синхронности хода двух часов. Пусть в момент времени t_A из А выходит луч света, отражается в В в момент времени t_B и возвращается назад в А в момент времени t’_A. Принимая во внимание принцип постоянства скорости света, находим

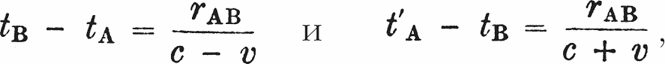
где r_АВ – длина движущегося стержня, измеренная в покоящейся системе.

Таким образом, наблюдатели, движущиеся вместе со стержнем, придут к выводу, что часы в точках А и В не идут синхронно, в то время как наблюдатели, находящиеся в покоящейся системе, объявили бы эти часы синхронными. Итак, мы видим, что не следует придавать абсолютного значения понятию одновременности. Два события, одновременные при наблюдении из одной координатной системы, уже не воспринимаются как одновременные при рассмотрении из системы, движущейся относительно данной системы.

В опубликованной четыре года назад работе уже была предпринята попытка ответить на вопрос, влияет ли тяготение на распространение света. Мы снова возвращаемся к этой теме, так как не удовлетворены прежним изложением этого вопроса. Кроме того, мы теперь еще раз убедились в том, что один из наиболее важных выводов указанной работы поддается экспериментальной проверке. Действительно, проходящие вблизи Солнца лучи, согласно излагаемой ниже теории, испытывают под влиянием поля тяготения Солнца отклонение. В результате такого отклонения должно произойти кажущееся увеличение углового расстояния между оказавшейся вблизи Солнца неподвижной звездой и самим Солнцем почти на одну дуговую секунду.

Развитие этих идей привело также к некоторым результатам, относящимся к тяготению. Так как изложение всех рассуждений было бы громоздким в ущерб ясности, то ниже приведем только некоторые элементарные соображения, с помощью которых удобно ориентироваться как в предпосылках, так и в логическом развитии теории. Выведенные в настоящей работе соотношения, даже если теоретическое основание их и соответствует действительности, являются верными только в первом приближении.

Пусть в однородном поле тяжести (ускорение силы тяжести) расположена покоящаяся координатная система К, ориентированная так, что силовые линии поля идут в отрицательном направлении оси z. Пусть в пространстве, свободном от гравитационных полей, находится вторая координатная система К’, которая равномерно ускоренно (с ускорением γ) движется в положительном направлении своей оси z. Для того чтобы не усложнять рассуждения, мы откажемся от теории относительности и рассмотрим обе системы в рамках привычной кинематики, а совершающиеся в них движения – в рамках обычной механики. Тогда материальные точки, которые не подвергаются влиянию со стороны других материальных точек, движутся относительно К, как и относительно К’, в соответствии с уравнениями

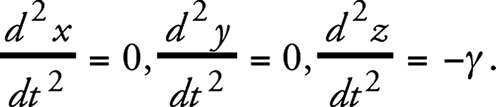
Для ускоренной системы отсчета К’ это следует прямо из принципа Галилея. Для покоящейся в однородном гравитационном поле системы отсчета К это следует из того опытного факта, что все тела в таком поле ускоряются равномерно и одинаково сильно. Этот опытный факт об одинаковом ускорении падения всех падающих в гравитационном поле тел является одним из наиболее общих фактов, установленных нами из наблюдений. Несмотря на это, закон этот не нашел еще отражения в основах нашей физической картины мира.

Однако мы придем к удовлетворительной интерпретации этого опытного закона, если допустим, что системы отсчета К и К’ физически в точности равноправны, другими словами, если мы допустим, что систему К равным образом можно рассматривать как систему, находящуюся в пространстве, свободном от поля тяжести, но при этом мы должны рассматривать К как равномерно ускоренную систему. При таком подходе нельзя говорить об абсолютном ускорении координатной системы, так же как нельзя в обычной теории относительности говорить об абсолютной скорости системы. С этой точки зрения одинаковое ускорение всех падающих тел в гравитационном поле очевидно.

До тех пор пока мы ограничиваемся чисто механическими явлениями, для которых справедлива механика Ньютона, мы уверены в равноценности систем К и К’. Однако представление наше будет достаточно глубоким только в том случае, если системы К и К’ окажутся равноценными относительно всех физических явлений, т. е. если законы природы по отношению к системе К полностью совпадут с законами природы по отношению к системе К’. Приняв это, мы получаем принцип, имеющий большое эвристическое значение, если он действительно справедлив. Действительно, с помощью теоретического изучения явлений, протекающих относительно равномерно ускоренной координатной системы, можно получить представление о ходе явлений в однородном гравитационном поле. Далее будет прежде всего показано, каким образом с точки зрения обычной теории относительности наша гипотеза приобретает значительную долю вероятности.

Теория относительности привела к выводу о росте инертной массы тела с увеличением содержащейся в нем энергии. Так, если приращение энергии есть Е, то приращение инертной массы составляет Е/с², где с – скорость света. Однако возникает вопрос: соответствует ли такому приращению инертной массы также приращение тяготеющей массы? Если нет, то тогда тело в одном и том же поле тяжести падало бы с разным ускорением, зависящим от энергии самого тела. Такой удовлетворительный результат теории относительности, согласно которому закон сохранения массы содержится в законе сохранения энергии, оказался бы несправедливым, хотя в этом случае для инертной массы и нужно было бы отбросить закон сохранения массы в его старой формулировке, но для тяготеющей массы он остался бы в силе.

Такой вывод очень маловероятен. С другой стороны, обычная теория относительности не дает ни одного аргумента, из которого можно было бы заключить, что вес тела зависит от содержащейся в нем энергии. Однако мы покажем, что из нашей гипотезы об эквивалентности систем отсчета К и К’ с необходимостью вытекает тяжесть энергии.

Итак, пусть две физические системы тел S₁ и S₂, снабженные измерительными приборами, расположены на оси Z системы отсчета К на расстоянии h друг от друга таким образом, что гравитационный потенциал в том месте, где находится система S₂, на γh больше гравитационного потенциала в месте нахождения S₁. Далее, пусть из S₂ посылается в S₁ определенное количество энергии Е в виде излучения и пусть при этом количество энергии измеряется с помощью приборов, которые, будучи установлены в одном и том же месте систем z и там друг с другом сравнены, оказались бы совершенно одинаковыми.

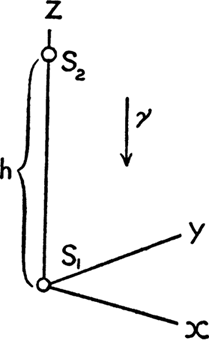
Заметим, что изначально о процессе переноса энергии излучением ничего сказать нельзя, потому что мы не знаем, как влияет поле тяжести на энергию излучения и на измерительные инструменты в S₁ и S₂. Тем не менее, согласно допущению об эквивалентности систем отсчета К и К’, мы можем на место системы К, находящейся в однородном поле тяжести, поставить свободную от тяготения систему отсчета К’, которая движется равномерно ускоренно в направлении положительных значений z, с осью z которой жестко связаны физические системы S₁ и S₂.

Обсудим процесс переноса энергии излучением из S₂ в S₁, если мы находимся в некоторой системе отсчета К₀, не обладающей ускорением. Будем считать, что в тот момент, когда энергия излучения Е₂ переносится из S₂ в S₁, система К’ обладает относительно системы К₀ нулевой скоростью. Лучи достигнут системы S₁ спустя время h/с (в первом приближении). В этот момент система S₁ обладает относительно К₀ скоростью h/с = v. Таким образом, согласно обычной теории относительности, достигающее S₁ излучение имеет не энергию Е₂, а большую энергию Е₁ которая в первом приближении связана с Е₂ соотношением:

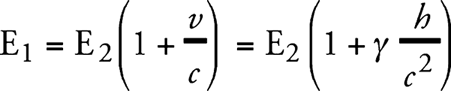
(1)

Согласно сделанному нами предположению, точно такое же соотношение справедливо и в том случае, когда рассматриваемый процесс протекает в системе К – неускоренной, но находящейся в гравитационном поле. В этом случае мы можем заменить γh потенциалом Ф гравитационного поля в точке, где находится S₂, если произвольная постоянная потенциала Ф в точке, где находится S₁, приравнивается нулю. Таким образом, получаем:

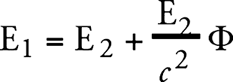
(1а)

Последнее есть закон сохранения энергии для рассматриваемого процесса. Энергия Е₁, приходящая в S₁ больше, чем измеренная такими же приборами энергия Е₂, которую отдает система в S₂, на величину потенциальной энергии массы Е₂/с² в поле тяжести. Таким образом, для выполнения закона сохранения энергии нужно к энергии Е перед ее испусканием из S₂ прибавить потенциальную энергию, которая соответствует (тяжелой) массе Е/с² в поле тяжести. Следовательно, наше допущение об эквивалентности систем отсчета К и К’ устраняет изложенную в начале этого параграфа трудность, чего не могла сделать обычная теория относительности.

Смысл полученного результата становится особенно ясным при рассмотрении следующего кругового процесса.

1. Энергия Е, измеренная в S₂, посылается в форме излучения из S₂ в S₁, где, согласно только что полученному результату, поглощается энергия Е × (1 + γh/с²), измеренная в S₁.

2. Тело W с массой М падает из S₂ в S₁, и при этом совершается работа Mγh.

3. Энергия Е из системы S₁ переносится на тело W, когда оно находится в S₁. Благодаря этому изменяется тяжелая масса М, и пусть ее новое значение равно М’.

4. Тело W снова поднимается в S₂, и при этом затрачивается работа М’ γh.

5. Энергия Е переносится с тела W на систему S₂.

В результате такого кругового процесса система S₁ приобрела энергию Е (γh/c²) и системой передана энергия М’γh – Mγh в форме механической работы. Следовательно, по закону сохранения энергии должно выполняться следующее соотношение:

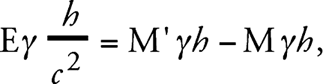
или

Окончательно получаем, что приращение тяжелой массы есть Е/c². Другими словами, оно равно тому приращению инертной массы, которое следует из теории относительности.

Еще более естественным образом этот результат вытекает из эквивалентности системы отсчета К и К’. Согласно этой эквивалентности, тяжелая масса, определенная относительно К, в точности равна инертной массе, определенной относительно К’. Таким образом, энергия должна обладать тяжелой массой, равной ее инертной массе. Так, если с помощью пружинных весов в системе отсчета К’ взвесить массу М₀, то эти весы (из-за инертности М₀) покажут кажущийся вес М₀γ. Если сообщить энергию Е массе М₀, то, согласно предположению об инерции энергии, пружинные весы покажут (М₀ + Е/c²) γ.

Согласно нашему основному предположению, то же самое должно наступить и при проведении опыта в системе отсчета К, т. е. в поле тяготения.

Пусть излучение, испускаемое в равномерно ускоренной системе отсчета К’ из S₂ по направлению к S₁, имеет относительно находящихся в S₂ часов частоту v₂. Тогда по прибытии в S₁ это излучение имеет относительно находящихся там точно таких же часов частоту уже не v₂, а большую частоту v₁, которая в первом приближении равна

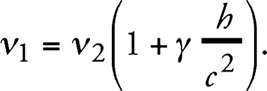
(2)

Действительно, снова вводя неускоренную систему отсчета К₀, относительно которой система отсчета К’ в момент испускания света имела нулевую скорость, то S₁ будет иметь относительно К₀ в момент прибытия излучения в S₁ скорость γ(h/с), откуда в силу принципа Допплера непосредственно получается соотношение (2).

Учитывая сделанное нами предположение об эквивалентности систем отсчета К и К’, полученное выражение справедливо и для покоящейся координатной системы К, в которой существует однородное поле тяжести, в том случае, когда в этой системе происходит описанный выше перенос энергии излучения.

Окончательно получаем, что луч света, испускаемый в области с определенным потенциалом тяготения из S₂ и имеющий при его испускании частоту v₂, измеренную часами, находящимися в S₂, обладает при его прибытии в S₁ другой частотой v₁, если последняя измеряется с помощью точно таких же часов, находящихся в S₁. Заменим γh через потенциал тяготения Ф, взятый в S₂ по отношению к S₁, потенциал которой принят равным нулю. Далее, что соотношение, полученное нами для однородного гравитационного поля, справедливо также и для полей другого вида.

В таком случае

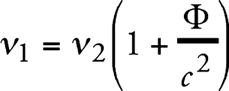
(2a)

Полученный результат (справедливый, напомним, согласно своему выводу, в первом приближении) прежде всего можно применить следующим образом. Пусть v₀ – частота некоторого элементарного источника света, которая измеряется с помощью часов U, находящихся в том же месте, где и сам источник. Эта частота не зависит от расположения источника света вместе с часами. Теперь представим, что источник и часы размещены, к примеру, на поверхности Солнца (там находится наша система S₂). Часть испущенного света доходит до Земли (S₁), где мы часами U точно такой же конструкции, что и упомянутые выше, измеряем частоту v приходящего света. Следовательно, согласно соотношению (2а), имеем

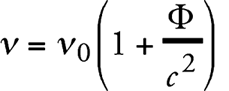
Здесь Ф – (отрицательная) разность гравитационных потенциалов между поверхностью Солнца и поверхностью Земли.

Согласно нашим представлениям, спектральные линии солнечного света должны немного сместиться по сравнению с соответствующими спектральными линиями земных источников света в красную область спектра, а именно, на относительную величину

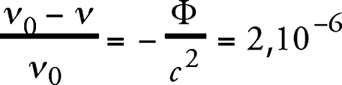
Это смещение можно было бы измерить, если бы были точно известны условия, при которых испускается солнечный свет. Но из-за того, что причины другого рода (такие как давление и температура) также влияют на положение центра тяжести спектральных линий, трудно установить, действительно ли существует выведенное выше соотношение, в котором учитывается влияние гравитационного потенциала.

При поверхностном рассмотрении может показаться, что соотношения (2) или (2а) не имеют смысла. Может ли быть, чтобы при непрерывном испускании света из S₂ он прибывал S₁ другой частотой, чем свет, вышедший из S₂? Тем не менее, ответ на этот вопрос прост. Дело в том, что мы не можем рассматривать v₂ и v₁ просто как частоты (т. е. как числа периодов в секунду), потому что мы еще не установили времени в системе отсчета К. Величина v₂ обозначает число периодов, отнесенное к единице времени часов U в S₂, a v₁ – число периодов, отнесенное к единице времени точно таких же часов U в S₁. У нас нет никаких оснований допускать, что часы, которые расположены в точках с различными гравитационными потенциалами, должны рассматриваться как одинаково идущие. Наоборот, мы обязательно должны определить время в системе отсчета К таким образом, чтобы число гребней и минимумов волн между S₂ и S₁ не зависело от абсолютного значения времени, потому что рассматриваемый процесс по своей природе стационарен. Если это условие не выполнено, то мы приходим к определению времени, которое будет явно входить в законы природы, что, конечно, неестественно и нецелесообразно.

Таким образом, нельзя сказать, что оба часовых механизма, в S₂ и S₁, показывают правильное «время». Так, если мы определяем время в S₁ часами U, то мы должны измерять время в S₂ часами, которые идут в [1 + (Ф/с²)] раза медленнее, чем часы U, если их сравнить с часами U в одном и том же месте. Это связано с тем, что измеренная подобными часами частота рассмотренного выше луча света при его отправлении из S₂

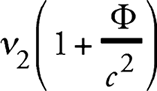
в согласии с формулой (2а), равна частоте v₁ того же луча света при его прибытии в S₁.

Отсюда вытекает следствие, представляющее фундаментальное значение для теории. Если скорость света измерять в различных местах ускоренной системы отсчета К’ в отсутствие гравитационного поля, пользуясь одинаково идущими часами U, то всюду будет получаться одно и то же значение. Исходя из нашего основного допущения, то же самое справедливо и для системы К. Однако из этого следует, что в местах с разными гравитационными потенциалами при измерении времени необходимо пользоваться по-разному идущими часами. В том месте, которое обладает гравитационным потенциалом Ф относительно начала координат, нужно при измерении времени применять часы, которые при перенесении их в начало координат шли бы в (1 + + Ф/с²) раза медленнее, чем те часы, которыми определяется время в начале координат. Если мы обозначим через с₀ скорость света в начале координат, то скорость света с в некотором месте с гравитационным потенциалом Ф будет равна

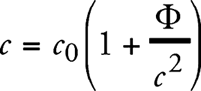
(3)

Согласно этой теории, принцип постоянства скорости света справедлив не в той формулировке, в какой он кладется в основу обычной теории относительности.

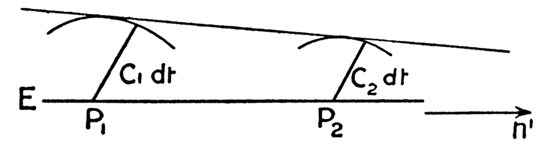
Из только что доказанного положения – скорость света в поле тяжести является функцией места – нетрудно с помощью принципа Гюйгенса доказать, что лучи света, распространяющиеся поперек поля тяжести, должны искривляться. В самом деле, пусть E – плоскость равной фазы некоторой плоской световой волны в момент времени t, а Р₁ и Р₂ – две точки на ней, расстояние между которыми равно единице. Точки Р₁ и Р₂ лежат в плоскости чертежа, которая выбрана так, что взятая по нормали к ней производная от Ф, а следовательно, и от с, обращается в нуль. Описывая около точек Р₁ и Р₂ окружности радиусами c₁dt и c₂dt и проводя к ним общую касательную, получаем плоскость равной фазы, точнее, ее сечение плоскостью чертежа для момента времени t + + dt, причем с₁ и с₂ представляют собой скорости света соответственно в точках Р₁ и Р₂. Следовательно, угол отклонения луча света на пути cdt составляет

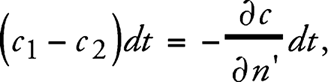
если мы его считаем положительным, когда луч света изгибается в сторону возрастания n’. Таким образом, угол отклонения на единицу пути луча света будет равен

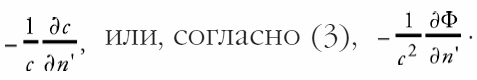
Наконец, для отклонения α, которое луч света испытывает на любом пути s в сторону n’, получаем выражение

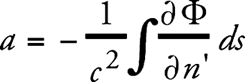
(4)

Такой же результат можно было бы получить также путем непосредственного рассмотрения распространения луча света в равномерно ускоренной системе отсчета К’, преобразования результата к системе К и затем обобщения на случай гравитационного поля произвольного вида.

Согласно выражению (4), проходящий мимо какого-либо небесного тела луч света испытывает отклонение в сторону убывания гравитационного потенциала, т. е. в сторону небесного тела. Это отклонение есть

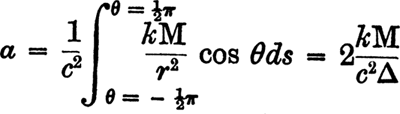
где k – гравитационная постоянная, М – масса небесного тела, Δ – расстояние от луча до центра небесного тела.

По этой причине луч света, проходящий мимо Солнца, испытал бы отклонение, равное 4 × 10^-6 = 0,83 секунды дуги. Благодаря искривлению луча угловое расстояние звезды от центра диска Солнца окажется увеличенным на эту величину. Так как звезды в соседних с Солнцем областях неба становятся видимыми при полных солнечных затмениях, то это следствие теории можно сравнить с опытом. Так, для планеты Юпитер ожидаемое смещение достигает примерно 0,01 доли указанного значения. Было бы крайне желательным, чтобы астрономы заинтересовались поставленным здесь вопросом даже и в том случае, если бы предыдущие рассуждения казались недостаточно обоснованными или фантастическими. Действительно, независимо от всякой теории, возникает вопрос: можно ли вообще современными средствами установить влияние гравитационных полей на распространение света.