Книга: КЭД – странная теория света и вещества
Назад: Лекция 2. Фотоны: частицы света
Дальше: Лекция 4. Нерешенные вопросы
Лекция 3. Электроны и их взаимодействия
Это третья из четырех лекций, посвященных весьма трудному предмету – квантовой электродинамике. И так как сегодня слушателей явно больше, чем было раньше, то, значит, многие из вас не слышали первых двух лекций. Им эта лекция покажется почти полностью непонятной. Те же, кто слышал первые две лекции, также сочтут эту лекцию непонятной, но они знают, что так и должно быть: я уже объяснял на первой лекции, что мы вынуждены описывать поведение Природы, как правило, непонятным образом.
В этих лекциях я хочу рассказать о наиболее изученном разделе физики – взаимодействии электронов со светом. Большая часть знакомых вам явлений основана на взаимодействии электронов со светом – например, вся химия и биология. Эта теория не охватывает только гравитационные и ядерные явления; все остальное в ней содержится.
На первой лекции мы обнаружили, что у нас нет наглядного механизма для описания даже такого простейшего явления, как частичное отражение света от стекла. Кроме того, мы не можем предсказать, отразится ли данный фотон, или пройдет сквозь стекло. Все, что мы можем сделать – посчитать вероятность конкретного события – отражения света в данном случае. (Она равна примерно 4 %, когда свет прямо падает на одиночную поверхность стекла; при наклонном падении вероятность отражения возрастает.)
Если мы имеем дело с вероятностями в обычных условиях, выполняются следующие «правила соединения»: 1) если событие может произойти взаимоисключающими способами, мы складываем вероятности всех различных способов; 2) если событие происходит поэтапно или в результате ряда независимых событий, мы перемножаем вероятности всех этапов (или событий).
В фантастическом и удивительном мире квантовой физики вероятности вычисляются как квадраты длин стрелок. Там, где в обычных условиях мы сложили бы вероятности, мы неожиданно для себя «складываем» стрелки; там, где умножили бы вероятности – «перемножаем» стрелки. Необычные ответы, получаемые при вычислении вероятностей таким способом, прекрасно соответствуют результатам эксперимента. Мне как раз очень нравится, что мы должны прибегать к таким необычным правилам и странным рассуждениям, чтобы понять Природу, и я всегда с удовольствием рассказываю об этом. За этим анализом Природы нет никакого скрытого механизма, «колесиков и шестеренок». Если вы хотите понять Ее, вы должны принять это.
Прежде чем перейти к основной части этой лекции, хочу показать вам еще один пример поведения света. Я расскажу об очень слабом свете одного цвета, который распространяется из источника S в детектор D (см. рис. 49) в виде одиночных фотонов. Поместим экран между источником и детектором и проделаем в нем два очень маленьких отверстия в точках А и В, находящихся на расстоянии в несколько миллиметров друг от друга. (Если расстояние между источником и детектором 100 сантиметров, размер дырочек должен быть меньше, чем десятая доля миллиметра.) Пусть точка А лежит на одной прямой с точками S и D, а точка В – несколько в стороне от А, не на этой прямой.
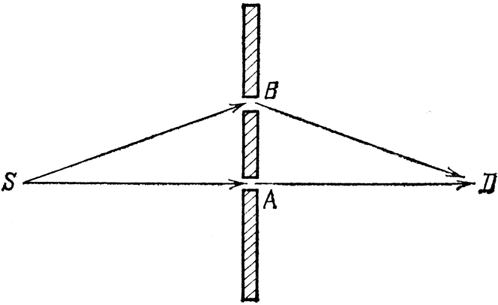
Рис. 49. Через каждое из двух маленьких отверстий (в точках A и В экрана, расположенного между источником S и детектором D, в случае, если открыто только одно) проходит примерно одинаковое количество света (в данном случае 1 %). Когда открыты оба отверстия, происходит «интерференция». Детектор щелкает от 0 до 4 % случаев в зависимости от расстояния между А и В (см. рис. 51, а).
Закрыв отверстие в В, получим в D некоторое количество щелчков, представляющих фотоны, прошедшие через А (скажем, детектор щелкает в среднем один раз на каждые 100 фотонов, испускаемых источником S, т. е. в 1 % случаев). Мы знаем из второй лекции, что если закрыть отверстие в А и открыть отверстие в В, получится примерно такое же, в среднем, количество щелчков – так как отверстия очень маленькие. (Когда мы слишком «сжимаем» свет, правила обычного мира – например, что свет распространяется прямолинейно – нарушаются.) Когда мы открываем оба отверстия, то получается сложный результат, связанный с наличием интерференции. При некотором расстоянии между отверстиями мы получаем щелчков больше, чем ожидаемые 2 % (вплоть до ~ 4 %); а чуть изменив это расстояние, вообще не получаем щелчков.
Естественно было бы ожидать, что открытие дополнительного отверстия всегда будет увеличивать количество света, попадающего в детектор. Но в действительности это не так. Поэтому неправильно говорить, что свет «распространяется или по одному пути, или по другому». Я все еще ловлю себя на том, что говорю: «Он распространяется по этому пути или по тому пути». Однако когда я так говорю, я должен иметь в виду, что подразумевается сложение амплитуд: имеется амплитуда прохождения фотона по одному пути и амплитуда прохождения по другому пути. Если амплитуды взаимно гасят друг друга, свет не будет распространяться, если даже, как в данном случае, открыты оба отверстия.
А вот еще одна странная особенность Природы, о которой мне хотелось бы рассказать. Предположим, мы помещаем в точках A и В специальные детекторы (можно сконструировать детектор, показывающий, прошел ли через него фотон) и теперь знаем, через какое отверстие (отверстия) проходит фотон, когда оба они открыты (см. рис. 50). Раз вероятность того, что одиночный фотон попадет из S в D, зависит только от расстояния между отверстиями, то, видимо, фотон как-то незаметно разделяется на два, а потом снова соединяется, не так ли? В соответствии с такой гипотезой, детекторы в А и В всегда должны срабатывать одновременно (возможно, вполсилы?), тогда как детектор в Dдолжен срабатывать с вероятностью от нуля до 4 % – в зависимости от расстояния между А и В.
А вот что происходит на самом деле: детекторы в А и В никогда не срабатывают одновременно – срабатывает детектор в А или детектор в В. Фотон не разделяется на два: он распространяется либо по одному, либо по другому пути.
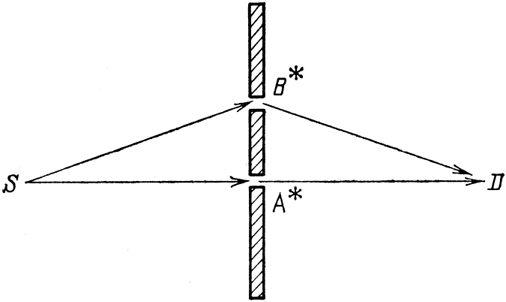
Рис. 50. Если в точках А и В расположены специальные детекторы (*), показывающие, по какому из путей распространяется свет при двух открытых отверстиях, эксперимент меняется. Поскольку фотон всегда проходит или через одно, или через другое отверстие (в случае, если вы за ними следите), имеются два конечных состояния: 1) сработали детекторы в А и D и 2) сработали детекторы в В и D. Вероятность того, что случится каждое из этих событий, равна примерно 1 %. Вероятности двух событий складываются обычным способом, и вероятность срабатывания детектора в D оказывается равной 2 % (см. рис. 51, б)
Более того, в этих условиях детектор в D срабатывает в 2 % случаев – а это просто сумма вероятностей прохождения через А и через В (1 % + 1 %). Значение 2 % не зависит от расстояния между А и В; интерференция исчезает, если в А и В поместить детекторы!
Природа так все устроила, что мы никогда не сможем понять, как она это делает: если мы ставим приборы, чтобы выяснить, по какому пути пойдет свет, – пожалуйста, мы можем это выяснить, но удивительные интерференционные эффекты исчезают. А если у нас нет приборов, показывающих, по какому пути идет свет, интерференционные эффекты восстанавливаются! В самом деле, очень странно!
Чтобы разобраться в этом парадоксе, позвольте напомнить вам самый важный принцип: для того чтобы правильно вычислить вероятность события, нужно очень внимательно отнестись к четкому определению законченного (полного) события – в частности, определить, каковы начальные и конечные условия эксперимента. Вы смотрите на оборудование до и после эксперимента и ищете изменения. Когда мы вычисляли вероятность попадания фотона из S в D без детекторов в А и В, то событием был просто щелчок детектора в D. Если щелчок в D был единственным изменением условий, то нельзя было сказать, по какому пути летел фотон, поэтому возникла интерференция.
Поместив детекторы в А и В, мы изменили задачу. Теперь оказывается, что есть два законченных события – две различные совокупности конечных условий: 1) сработали детекторы в А и D; 2) сработали детекторы в В и D. Если у эксперимента имеется несколько допустимых конечных условий, надо вычислять вероятность каждого как отдельного законченного события.
Для вычисления амплитуды того, что сработают детекторы в А и D, мы умножаем стрелки, которые представляют следующие этапы: фотон летит из S в A; фотон летит из А в D; детектор в D срабатывает. Квадрат длины получившейся стрелки есть вероятность этого события – 1 % – такая, как при закрытом отверстии В, так как в обоих случаях этапы одинаковы. Другое законченное событие – срабатывание детекторов в В и D. Вероятность этого события вычисляется таким же способом, и результат такой же, как раньше – примерно 1 %.
Если нас интересует вероятность срабатывания детектора в D, причем все равно, сопровождается оно срабатыванием детектора в А или в В, то эта вероятность равна простой сумме вероятностей двух событий – 2 %. Вообще, если в системе остается что-то, благодаря чему мы могли бы определить путь фотона, мы имеем различные «конечные состояния» (различимые конечные условия) и складываем вероятности, а не амплитуды всех конечных состояний.
Я указал на эти обстоятельства, потому что чем больше вы наблюдаете странное поведение Природы, тем сложнее построить наглядную модель, объясняющую даже простейшие явления. И теоретическая физика отказалась от этого.
На первой лекции мы увидели, как можно разделить событие на взаимоисключающие пути и как можно «сложить» стрелки для каждого пути. На второй лекции мы узнали, как можно разделить путь на последовательные этапы, как можно представить стрелку для каждого этапа в виде преобразования единичной стрелки и как «перемножить» стрелки для каждого этапа путем последовательных сжатий и поворотов. Следовательно, мы знакомы со всеми необходимыми правилами рисования и соединения стрелок (представляющих кусочки событий) для получения результирующей стрелки, квадрат длины которой является вероятностью наблюдаемого реального события.
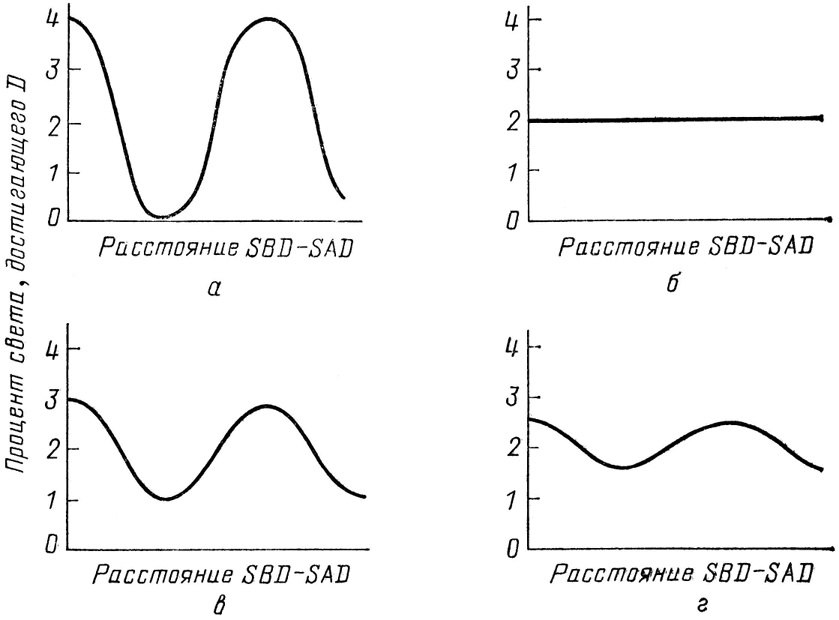
Рис. 51. Если в А и В нет детекторов, возникает интерференция: доля прошедшего света колеблется от 0 до 4 % (а). Если в А и В имеются детекторы, надежные на 100 %, интерференция не возникает – доля попавшего в D света постоянна, 2 % (б). Если детекторы в А и В не надежны на все 100 % (т. е. если иногда в А и В не остается ничего, что можно было бы зарегистрировать), имеются три возможных конечных условия: А и D сработали, В и D сработали, только Dсработал. Окончательная кривая на рисунках обусловлена, следовательно, смесью вкладов всех возможных конечных условий. При уменьшении надежности детекторов в А и В интерференция усиливается. Так, в случае (в) детекторы менее надежны, чем в случае (г). Принцип, которым надо руководствоваться, встретившись с интерференцией, таков: необходимо независимо вычислить вероятность каждого из различных конечных условий путем сложения стрелок и возведения в квадрат длины результирующей стрелки; после этого вероятности складываются обычным образом.
Естественно поинтересоваться, насколько далеко мы можем зайти в этом дроблении события на все более простые подпроцессы. Каков наименьший возможный кусочек события? Имеется ли конечное число кусочков, из которых можно образовать любое явление, связанное со светом и электронами? Имеется ли ограниченное число «букв» в этом языке квантовой электродинамики, комбинируя которые в «слова» и «предложения», можно описать почти каждое явление Природы?
Ответ: да; число равно трем. Существуют только три основных действия, необходимых для получения всех явлений, связанных со светом и электронами.
Прежде чем рассказать вам об этих действиях, мне надо должным образом познакомить вас с действующими лицами. Действующие лица – это фотоны и электроны. Фотоны, частицы света, подробно обсуждались на первых двух лекциях. Электроны были открыты в 1895 г. как частицы: вы могли пересчитать их, вы могли поместить один из них на каплю масла и измерить его электрический заряд. Постепенно стало очевидным, что движение этих частиц объясняет электрические явления в проводах.
Вскоре после открытия электронов стали думать, что атомы подобны маленьким Солнечным системам, состоящим из центральной тяжелой части (названной ядром) и электронов, вращающихся по «орбитам», подобно планетам, вращающимся вокруг Солнца. Если вы считаете, что атомы устроены именно так, вы находитесь в 1910 г.
В 1924 г. Луи де Бройль обнаружил волновые свойства электронов, а вскоре сотрудники лабораторий «Белл» К. Дж. Дэвиссон и Л. Джермер бомбардировали кристалл никеля электронами и показали, что, подобно рентгеновским лучам, электроны отражаются под особыми углами, которые можно вычислить, используя формулу де Бройля для длины волны электрона.
Если рассматривать фотоны на больших расстояниях, много больших, чем требуется для одного оборота стрелки часов, наблюдаемые нами явления довольно точно описываются правилами типа «свет распространяется по прямой». Это происходит потому, что вблизи пути наименьшей длительности имеется достаточно путей, чтобы усилить друг друга, и достаточно других путей, чтобы погасить друг друга. Но если пространство, по которому летит фотон, становится слишком маленьким (как в случае малых отверстий в экране), эти правила не выполняются, и мы обнаруживаем, что свет не распространяется по прямой, что два отверстия создают интерференцию, и т. д. То же самое и с электронами: на больших расстояниях они движутся как частицы, по определенным траекториям. Но на малых расстояниях, например внутри атома, места так мало, что не существует основного пути, не существует «орбиты»; электроны могут распространяться по множеству путей, каждый из которых характеризуется некоторой амплитудой. Очень важным становится явление интерференции, и мы вынуждены складывать стрелки, чтобы предсказать, где может находиться электрон.
Весьма интересно отметить, что сначала электроны выглядели как частицы, а их волновые свойства были обнаружены позже. С другой стороны (если не считать Ньютона, ошибочно полагавшего, что свет имеет «корпускулярный» характер), свет сначала всем казался волнами, а свойства его как частицы были открыты позже. В действительности и электроны, и свет ведут себя до некоторой степени как волны, а до некоторой степени как частицы. Чтобы не изобретать новых слов, вроде «волница», условимся называть такие объекты «частицами». Но все мы знаем, что они подчиняются тем правилам рисования и соединения стрелок, которые я объяснял. Оказалось, что все «частицы» в Природе – кварки, глюоны, нейтрино и т. д. (которые будут обсуждаться в следующей лекции) – ведут себя таким квантово-механическим образом.
Итак, теперь я представлю вам три основных действия, из которых возникают все явления, связанные со светом и электронами.
– Действие 1: Фотон летит из одного места в другое.
– Действие 2: Электрон летит из одного места в другое.
– Действие 3: Электрон испускает или поглощает фотон.
Каждое из этих действий имеет амплитуду (стрелку), которая может быть вычислена по определенным правилам.
Через несколько минут я сообщу вам эти правила, или законы, при помощи которых можно построить целый мир (как всегда, за исключением атомного ядра и гравитации!).
Сцена, на которой разыгрываются эти действия, – не просто пространство, а пространство и время. До сих пор я не затрагивал проблем, связанных со временем, например, когда именно фотон покинул источник и когда именно достиг детектора. Хотя на самом деле пространство трехмерно, на графиках, которые я буду рисовать, я сведу его к одномерному: я буду откладывать пространственное положение объекта по горизонтальной оси, а время – по вертикальной.
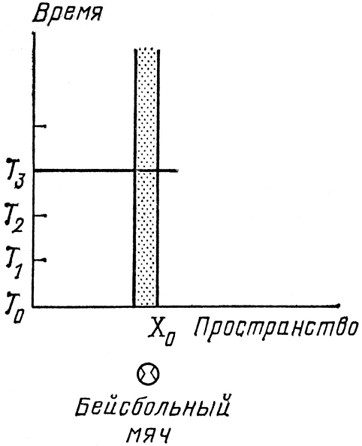
Рис. 52. Сцена, на которой разыгрываются все действия во Вселенной – это пространство-время. Обычно имеющее четыре измерения (три пространственных и одно временное), пространство-время здесь будет представляться двумерным – с одним пространственным (горизонтальная ось) и одним временным (вертикальная ось) измерениями. Когда бы мы ни по-смотрели на бейсбольный мяч (например, в момент Т3), он занимает одно и то же место. Так образуется «полоса бейсбольного мяча», растущая со временем вверх.
Первое событие, которое я собираюсь изобразить в пространстве и времени, или в пространстве-времени, как я мог бы его небрежно назвать, – это лежащий неподвижно бейсбольный мяч (см. рис. 52). В четверг утром (этот момент времени я обозначу T0) мяч находится в некотором месте (которое я обозначу Х0). Поскольку мяч неподвижен, несколько позже, в момент времени Т1, мяч занимает то же место. Несколько позже, в Т2, мяч все еще в Х0. Поэтому диаграмма, изображающая неподвижный мяч, – вертикальная полоса, поднимающаяся строго вверх, как бы вся заполненная мячом.
Что произойдет, если мяч движется в невесомости, в космическом пространстве, и летит прямо к стене? Пусть в четверг утром (Т0) он начинает свой путь в Х0 (см. рис. 53). Через некоторое время он оказывается на другом месте, в X. Продолжая двигаться, мяч образует наклонную «полосу мяча» на пространственно-временной диаграмме. Ударившись о стенку (стоящую неподвижно, и поэтому изображаемую вертикальной полосой), мяч движется назад по другой пространственно-временно́й траектории. Точно в то же место (Х0), откуда вылетел, но в другую временную точку (Т6).
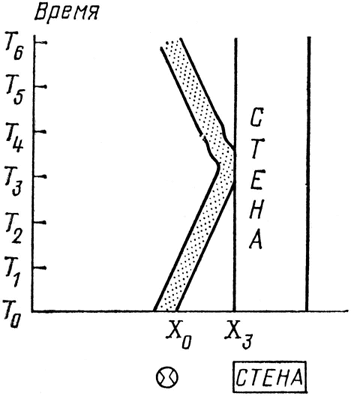
Рис. 53. Бейсбольный мяч, летящий под прямым углом к стенке и затем отскакивающий на первоначальное место (показанное под графиком), движется в одном измерении, а на графике изображается в виде наклонной «полосы мяча». В моменты времени Т1 и Т2 мяч приближается к стенке, в момент Т3 ударяется в нее и начинает обратный путь.
Что касается временной шкалы, то удобней откладывать время не в секундах, а в значительно меньших единицах. Поскольку мы будем иметь дело с очень быстро движущимися электронами и фотонами, я хочу, чтобы линия под углом 45° изображала нечто, движущееся со скоростью света. Например, для частицы, летящей со скоростью света из Х1Т2 в Х2Т2 горизонтальное расстояние между Х1 и Х2 равно вертикальному расстоянию между Τ1 и Т2 (см. рис. 54). Масштабный множитель, на который растянута ось времени (чтобы линия под углом 45° изображала частицу, движущуюся со скоростью света), называется с, и вы увидите, что эти с мельтешат повсюду в формулах Эйнштейна – это следствие неудачного выбора в качестве единицы времени секунды, а не времени, за которое свет пролетает 1 метр.
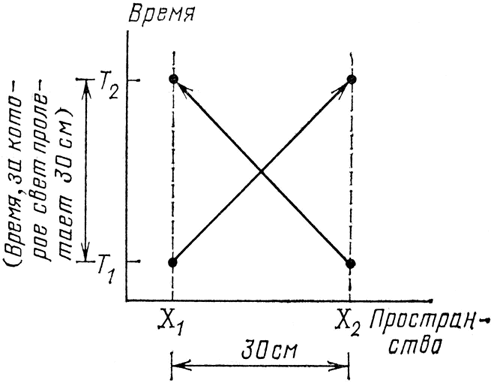
Рис. 54. В этих графиках я буду использовать такую шкалу времени, что частицы, летящие со скоростью света, будут распространяться под углом в 45° в пространстве-времени. Время, которое нужно свету, чтобы пролететь 30 см – из Х1 в Х2 или из Х2 в Х1 – порядка одной миллиардной доли секунды.
Теперь давайте подробно рассмотрим первое фундаментальное действие: фотон летит из одного места в другое. Я произвольно изображу это действие волнистой линией, соединяющей А и В. Мне следует быть точнее: надо было бы сказать, что фотон, про который известно, что он находится в данный момент времени в данном месте, имеет некоторую амплитуду попасть в другое место в другой момент времени. На моем пространственно-временном графике (см. рис. 55) у фотона в точке А (с координатами X1 и T1) имеется амплитуда попасть в точку В (с координатами Х2 и Т2). Величину этой амплитуды я буду называть Р(А – В).
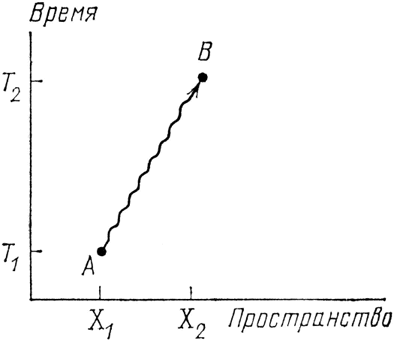
Рис. 55. Фотон (изображенный волнистой линией) с некоторой амплитудой может попасть из одной точки пространства-времени (А) в другую точку (В). Эта амплитуда, которую я буду называть Р(А – В), вычисляется по формуле, зависящей только от разности пространственных (Χ1– Χ2) и временных (Т2–Т1) координат. На самом деле это простая формула: Р(А – В) равна обратной величине разности квадрата этих величин – «интервала» I, который можно записать как (X2–X1)2–(T2–T1)2.
Для длины стрелки Р(А – В) имеется формула. Эта формула – один из великих законов Природы, и она очень проста. Она зависит от разницы пространственных и временных координат двух точек. Математически эта разница может быть выражена как (Х2–Х1) и (T2–T1).
Основной вклад в Р(А – В), как и следовало ожидать, дает движение с обычной скоростью света – когда (Х2–Х1) равно (Т2–T1). Но кроме того, имеется амплитуда распространения света быстрее (или медленнее) обычной скорости света. На предыдущей лекции вы узнали, что свет распространяется не только по прямой: теперь вы узнаете, что он распространяется не только со скоростью света!
Вас может удивить то, что имеется амплитуда распространения света со скоростью большей или меньшей скорости света с. Эти амплитуды очень малы по сравнению со вкладом от скорости с. В действительности такие вклады взаимно гасятся при движении света на большие расстояния. Однако если расстояния малы – как во многих диаграммах, которые я буду рисовать, – другие возможности становятся очень существенными, и их надо учитывать. Итак, вот первое основное действие, первый основной закон физики – фотон летит из одного места в другое. Это объясняет всю оптику; это полная теория света! Правда, не совсем: я не учитывал поляризацию (как всегда) и взаимодействие света с веществом (что приводит меня ко второму закону).
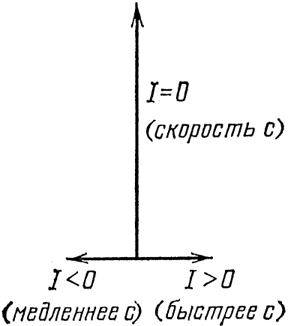
Рис. 56. Если свет распространяется со скоростью с, интервал I=0 и имеется большой вклад, направленный на 12 часов. Если I>0, имеется малый вклад, обратно пропорциональный I, направленный на 3 часа. Если I<0, имеется аналогичный вклад, направленный на 9 часов. Итак, у света есть амплитуды распространяться быстрее или мед-леннее скорости с, но эти амплитуды взаимно гасятся на больших расстояниях.
Второе действие, лежащее в основе квантовой электродинамики, таково: электрон летит в пространстве-времени из точки А в точку В. (Представим на минуту, что этот электрон – упрощенный, фальшивый электрон, не имеющий поляризации, – то, что физики называют электрон «со спином нуль». В действительности у электронов есть своя поляризация, которая, ничего не добавляя к основным идеям, лишь несколько усложняет формулы.) Формула амплитуды этого действия, которую я назову Е(А – В), также зависит от (Х2–X1) и (Т2–T1) (в той же комбинации, как описано в сноске на с. 103). Кроме того, она зависит от числа, назову его «n», которое, будучи однажды определено, позволяет привести все наши расчеты в согласие с экспериментом. (Впоследствии мы увидим, как определить значение п.) Это довольно сложная формула, и я, к сожалению, не знаю, как ее просто объяснить. Однако вам может быть интересно узнать, что формула для Р(А – В) – фотон летит из точки в точку – такая же, как формула для Е(А – В) – электрон летит из точки в точку – если п положить равным нулю.
Третье основное действие таково: электрон излучает или поглощает фотон (не важно, поглощает или излучает). Я буду называть это действие «соединением», «связью» или «взаимодействием». Чтобы отличать на диаграммах электроны от фотонов, я буду изображать каждый электрон, движущийся в пространстве-времени, прямой линией. Поэтому каждое взаимодействие (связь) представляет собой соединение прямых линий с волнистой линией (см. рис. 58). Амплитуда того, что электрон испустит или поглотит фотон, не выражается какой-либо сложной формулой; она ни от чего не зависит – это просто число! Эту константу связи я обозначу j – ее значение примерно –0,1; сжатие примерно равно до 0,1 и полуоборот.
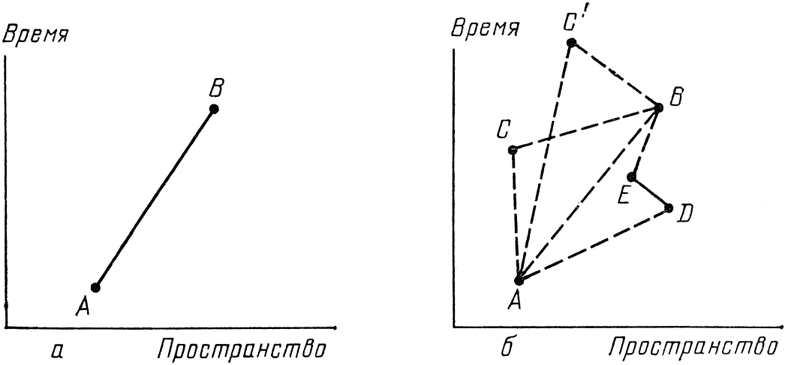
Рис. 57. У электрона имеется амплитуда попасть из одной точки пространства-времени в другую – я буду называть ее Е(А – В). Хотя я и буду изображать Е(А – В) прямой линией, соединяющей две точки (а), мы можем считать ее суммой многих амплитуд (б) – среди которых имеется амплитуда повернуть в точках С или С' на «двухпрыжковом» пути, и амплитуда по-вернуть в точках D и Е на «трехпрыжковом» пути – помимо прямого пути из А в В. Число поворотов электрона может быть любым, от нуля до бесконечности, а повороты могут произойти в любой точке пространства-времени. И все это учитывается величиной Е(А – В).
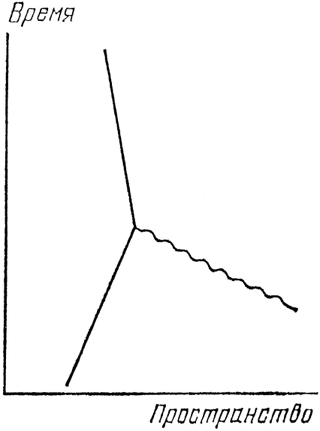
Рис. 58. У электрона, изображаемого прямой линией, есть не-которая амплитуда излучить или поглотить фотон, изображаемый волнистой линией. Поскольку амплитуды поглощения или из-лучения одинаковы, я буду называть и то и другое «взаимодействием» или «связью». Амплитуда взаимодействия есть число, которое я назову j, оно пример-но равно –0,1 (это число иногда называют «зарядом»).
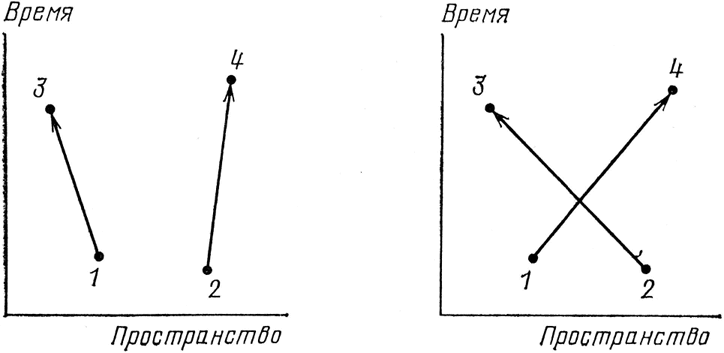
Рис. 59. Чтобы вычислить вероятность того, что электроны по-падут из точек 1 и 2 пространства-времени в точки 3 и 4, вычисляем стрелку «первого пути» (из точки 1 в 3 и из 2 в 4), используя формулу для Е(А – В). Затем вычисляем стрелку «второго пути» – «перекрестного» (из точки 1 в 4 и из 2 в 3). Складываем стрелки «первого пути» и «второго пути» и полу-чаем хорошее приближение для результирующей стрелки. (Это справедливо для фальшивого, упрощенного электрона «со спином нуль». Если учитывать поляризацию электрона, то надо не складывать, а вычитать стрелки друг из друга).
Это все, что касается основных действий, – если не считать небольших усложнений, связанных с поляризацией, которую мы по-прежнему не рассматриваем. Наша следующая задача: связать между собой эти три действия, чтобы рассматривать несколько более сложные явления.
В качестве первого примера давайте вычислим вероятность того, что два электрона попадут из пространственно-временных точек 1 и 2 в точки 3 и 4 (см. рис. 59). Такое событие может произойти несколькими способами. Первый способ состоит в том, что электрон из точки 1 летит в точку 3 (надо подставить 1 и 3 в формулу Е(А – В), я запишу это в виде Е(1–3), а электрон из точки 2 летит в точку 4. Поскольку это два независимых подпроцесса, надо умножить одну стрелку на другую, чтобы получить стрелку для этого первого способа, которым могло произойти событие. Поэтому мы пишем такую формулу для стрелки «первого способа»: Е(1–3)×Е(2–4).
Другой способ, которым может произойти данное событие: электрон из точки 1 летит в точку 4, а электрон из точки 2 – в точку 3. Это опять два независимых подпроцесса. Стрелка «второго способа» равна Е(1–4)×Е(2–3), и мы складываем ее со стрелкой «первого способа». Это хорошее приближение для амплитуды данного события.
Чтобы провести более точный расчет, который бы лучше согласовывался с результатами эксперимента, мы должны рассмотреть другие способы, которыми может произойти данное событие. Например, в каждом из двух основных способов один электрон мог отправиться в какое-то новое и чудесное место и испустить фотон (см. рис. 60). Тем временем другой электрон мог попасть в какое-то другое место и поглотить там этот фотон. Вычисление амплитуды первого из этих новых способов заключается в умножении следующих амплитуд: электрон летит из точки 1 в новое и чудесное место 5(где он излучает фотон), затем летит из 5 в 3; другой электрон летит из точки 2 в другое место 6 (где он поглощает фотон), затем летит из 6 в 4. Мы не должны также забывать про амплитуду попадания фотона из 5 и 6. Я напишу амплитуду такого способа осуществления события в первоклассном математическом виде, а вы можете следить: E(1–5)×j×E(5–3)×E(2–6)×j×E(6–4)×P(5–6) – множество сжатий и поворотов. (Предоставляю вам самим написать формулу для другого случая, когда электрон из точки 1 попадает в точку 4, а электрон из точки 2 попадет в точку 3.)
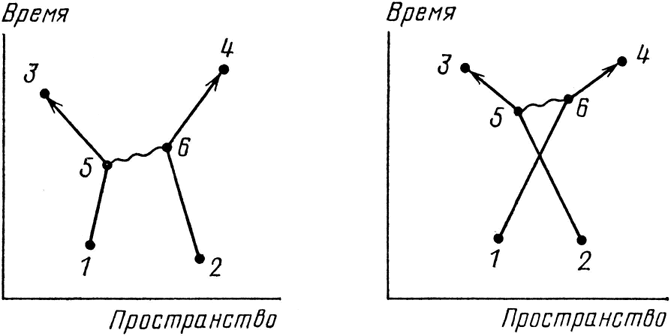
Рис. 60. Вот два других способа, которыми может произойти событие на рис. 59: на каждом рисунке в точке 5 испускается, а в точке 6 поглощается фотон. Конечные условия здесь такие же, как и в двух предыдущих случаях – два электрона входят и два выходят – так что результаты неотличимы. Поэтому стрелки для этих «других способов» надо прибавить к стрелкам для всех способов на рис. 59, тогда получится еще лучшее приближение для результирующей стрелки всего события.
Но постойте: положение точек 5 и 6 может быть любым в пространстве и времени, не правда ли, – и надо вычислить и сложить стрелки для всех этих положений. Как видите, предстоит немало работы. Дело не в том, что правила очень сложны – это похоже на игру в шашки: правила простые, но вы применяете их снова и снова. Итак, наши сложности при расчете связаны с тем, что нужно нагромоздить целую кучу стрелок. Вот почему студенты целых четыре года учатся делать это эффективно – а ведь мы рассматриваем легкую задачу! (Когда задачи становятся слишком трудными, мы решаем их с помощью компьютера!)
Я хотел бы отметить следующее относительно поглощения и излучения фотонов. Если точка 6расположена позже, чем точка 5, мы можем сказать, что фотон излучился в 5 и поглотился в 6 (см. рис. 61). Если точка 6 расположена раньше, чем 5, мы, вероятно, предпочли бы сказать, что фотон излучился в 6 и поглотился в 5. Но с таким же успехом мы могли бы сказать, что фотон движется вспять во времени! Нам, однако, не надо беспокоиться о том, в каком направлении в пространстве-времени летит фотон; все это учтено в формуле для Р(5–6), и мы говорим, что произошел «обмен» фотоном. Разве не замечательно, что Природа так проста!
Далее, вдобавок к обмену фотоном между точками 5 и 6 возможен обмен другим фотоном – между точками 7 и 8 (см. рис. 62). Я слишком устал, чтобы выписывать все основные действия, стрелки которых должны быть перемножены, но, как вы могли заметить, каждая прямая линия дает Е(А – В), каждая волнистая линия дает Р(А – В), а каждое взаимодействие дает j. Итак, имеются шесть Е(А – В), два Р(А – В) и четыре j – и так для любых возможных точек 5, 6, 7 и 8! Это дает миллиарды маленьких стрелочек, которые надо перемножить и потом сложить!
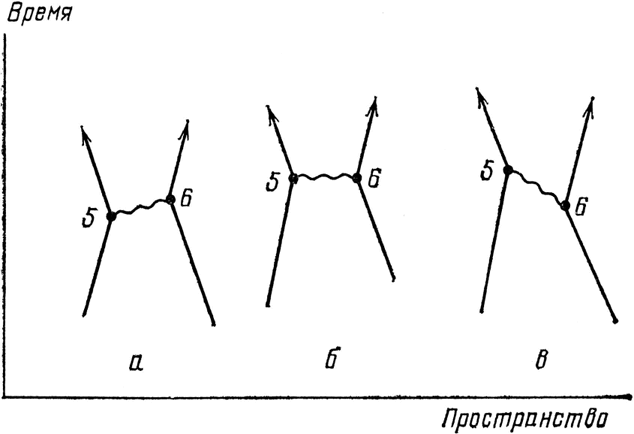
Рис. 61. Поскольку у света имеется амплитуда лететь быстрее или медленнее обычной скорости света, можно считать, что во всех трех примерах фотоны излучались в точке 5 и поглощались в точке 6. И это несмотря на то, что в примере б фотон был излучен и поглощен в одно и то же время, а в примере в был излучен позже, чем поглощен. В последней ситуации вы, может быть, предпочли бы сказать, что фотон был излучен в 6 и поглощен в 5, ведь иначе фотон должен был бы лететь вспять во времени! Постольку поскольку это касается вычислений (и Природы), это все равно (и все возможно). Поэтому мы говорим просто, что произошел «обмен» фотоном, и подставляем пространственно-временные положения в формулу для Р(А – В).
Кажется, вычисление амплитуды этого простого события – дело безнадежное. Однако если вы студент и вам надо получить диплом, то вы работаете.
Но надежда на успех есть. Она основана на этом магическом числе j. В первых двух способах, которыми может произойти событие, j не фигурирует; в следующем способе имеется j×j, а в последнем рассмотренном нами – j×j×j×j. Так как j×j меньше 0,01, это означает, что длина стрелки для этого способа, вообще говоря, составляет меньше 1 % длины стрелки для первых двух способов. Стрелка с j×j×j×j будет меньше, чем 1 % от 1 %, т. е. одна десятитысячная часть в сравнении со стрелками, не содержащими j. Если у вас достаточно компьютерного времени, можете рассмотреть возможности, содержащие j6 – одну миллионную часть, при этом ваши расчеты будут соответствовать точности экспериментов. Вот так и рассчитываются простые события. Именно таким образом все и устроено!
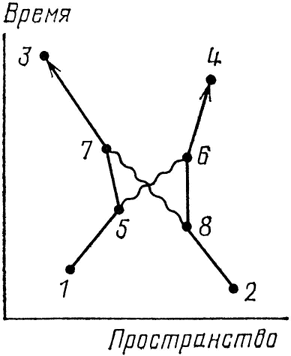
Рис. 62. Событие на рис. 59 может произойти еще одним способом (третьим): путем обмена двумя фотонами. Для этого способа (как мы увидим подробнее ниже) имеется множество диаграмм, одна из которых здесь показана. Стрел-ка для этого способа учитывает все возможные положения промежуточных точек 5, 6, 7 и 8, и по-этому вычислять ее очень трудно. Поскольку j меньше, чем 0,1, дли-на этой стрелки, вообще говоря, меньше, чем одна десятитысячная (так как в процессе происходят четыре взаимодействия) – по срав-нению с не содержащими j стрелками «первого способа» и «второго способа» на рис. 59.
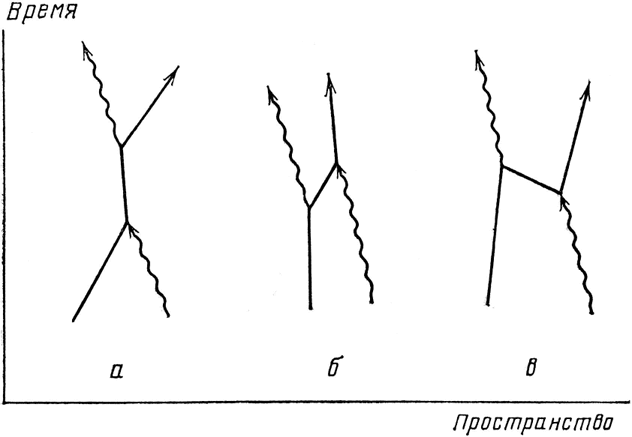
Рис. 63. При рассеянии света фотон может сначала поглощаться электроном, а потом излучаться (а). Такая последовательность событий необязательна, как видно из примера б. Пример иллюстрирует странную, но реальную возможность: электрон излучает фотон, мчится вспять во времени, чтобы поглотить фотон, а затем снова летит вперед во времени.
Рассмотрим теперь другое событие. Мы начинаем, имея фотон и электрон, и заканчиваем, имея фотон и электрон. Один из способов осуществления этого события состоит в том, что сначала фотон поглощается электроном, электрон немного пролетает и испускает новый фотон. Этот процесс называется рассеянием света. Рисуя диаграммы и проводя расчеты для рассеяния, мы должны учитывать некоторые необычные возможности (см. рис. 63). Например, электрон может испустить фотон до того, как поглотит фотон (б).
Еще более странная возможность (в) состоит в том, что электрон испускает фотон, затем летит вспять во времени, поглощает фотон и затем снова летит вперед во времени. Путь, пройденный таким «движущимся вспять» электроном, может быть настолько длинным, что проявится в реальном физическом эксперименте в лаборатории. Его поведение учитывается этими диаграммами и выражением Е(А – В).
Движущийся вспять электрон, если его рассматривать в правильном направлении времени, оказывается таким же, как обычный электрон, за исключением того, что притягивается к нормальному электрону – мы говорим, что у него «положительный заряд». (Если бы я учел поляризацию фотонов, стало бы очевидно, почему j у движущегося вспять электрона имеет обратный знак, делая его заряд положительным.) По этой причине он называется «позитроном». Позитрон – это частица, родственная электрону. Он представляет собой пример «античастицы».
Это общее явление. Каждая частица в Природе обладает амплитудой движения вспять во времени и, следовательно, имеет античастицу. Когда частица и античастица сталкиваются, они аннигилируют и образуют другие частицы. (При аннигиляции электрона и позитрона получается обычно фотон или два фотона.) А что же фотоны? Как мы видели, фотоны совершенно не изменяются при движении вспять во времени – поэтому они сами себе античастицы. Видите, как ловко мы сделали исключение частью правила.
Я хотел бы показать вам, как выглядит этот движущийся вспять электрон, когда сами мы движемся вперед по времени. Проведя для наглядности ряд параллельных прямых, я разделю диаграмму на временные отрезки точками Т0…, Т10 (см. рис. 64). Мы начинаем в момент времени Т0: электрон и фотон движутся навстречу друг другу. Внезапно в момент времени Т3 фотон превращается в две частицы, позитрон и электрон. Позитрон живет недолго, вскоре, в момент Т6, он сталкивается с электроном, и при их аннигиляции образуется новый фотон. Тем временем электрон, образовавшийся из первоначального фотона, продолжает двигаться в пространстве-времени.
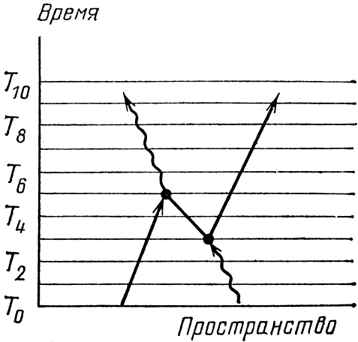
Рис. 64. Рассмотрим пример в на рис. 63, двигаясь только вперед во времени (как мы вынуждены поступать в лаборатории). От момента времени Т0 до Т3 мы видим, что электрон и фотон летят навстречу друг другу. Внезапно в момент Т3 фотон «распадается» и появляются две частицы: электрон и частица ново-го типа – «позитрон» (представляющая собой электрон, движущийся вспять во времени). Позитрон движется навстречу исходному электрону. В момент времени Т5 позитрон аннигилирует с исходным электроном и образуется новый фотон. Тем временем образованный исходным фотоном электрон продолжает лететь вперед по пространству-времени. Такая последова-тельность событий наблюдается в лаборатории, она автоматически, не требуя никаких изменений, учитывается формулой Е(А – В).
Следующее, о чем я хотел бы рассказать, – это электрон в атоме. Чтобы понять поведение электронов в атомах, мы должны добавить в нашу картину мира еще один важный объект – тяжелое ядро в центре атома, содержащее по крайней мере один протон. (Протон – это ящик Пандоры, который мы откроем на следующей лекции.) Я не буду объяснять вам в этой лекции истинные законы поведения ядра – они очень сложны. Но в данном случае, когда ядро спокойно, мы можем приближенно описать его как частицу с амплитудой попадания из одной точки пространства-времени в другую по формуле Е(А – В), но со значительно большей величиной параметра п. Поскольку ядро по сравнению с электроном очень тяжелое, мы можем приближенно считать, что, двигаясь во времени, оно стоит практически на одном месте в пространстве.
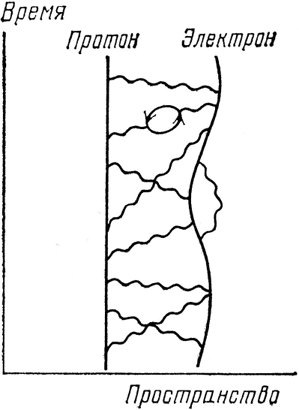
Рис. 65. Электрон удерживается вблизи от ядра атома путем обмена фотонами с протоном («ящик Пандоры», в который мы заглянем в четвертой лекции). Воспользуемся пока приблизительным определением протона как неподвижной частицы. Здесь показан атом водорода, состоящий из протона и электрона, обменивающихся фотонами.
Простейший атом – атом водорода – состоит из протона и электрона. Протон удерживает танцующий вокруг него электрон, обмениваясь с ним фотонами (см. рис. 65). Атомы, содержащие более одного протона и соответствующее количество электронов, также рассеивают свет (атомы атмосферного воздуха рассеивают солнечный свет и делают небо голубым), но на диаграммах для таких атомов было бы так много прямых и волнистых линий, что получилась бы полная неразбериха!
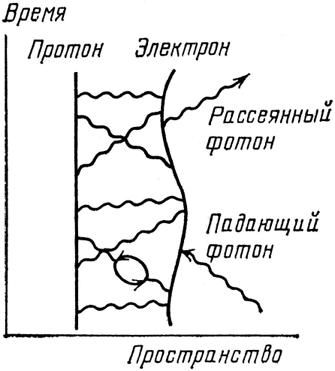
Рис. 66. Рассеяние света электроном атома – это явление, лежащее в основе частичного отражения света стеклом. Диаграмма показывает один из способов, которым такое со-бытие может произойти в атоме водорода.
Теперь я хотел бы показать вам диаграмму рассеяния света электроном в атоме водорода (см. рис. 66). В то время как электрон и ядро обмениваются фотонами, извне к атому прилетает фотон, сталкивается с электроном и поглощается им; затем излучается новый фотон. (Как обычно, надо рассмотреть и другие возможности, например, сначала излучается новый фотон, а потом уже поглощается старый фотон.) Амплитуды всех возможных способов рассеяний фотона электроном могут быть просуммированы в результирующую стрелку посредством операций сжатия и поворота. (Впоследствии мы будем называть эту стрелку «S».) Ее величина зависит от ядра и расположения электронов в атоме, она различна для различных веществ.
Теперь давайте снова посмотрим на частичное отражение света от стеклянной пластинки. Как оно происходит? Я говорил, что свет отражается от передней и от задней поверхностей. Говоря о поверхностях, я делал некоторое упрощение. На самом деле поверхности никак не действуют на свет. Входящий в стекло фотон рассеивается электронами атомов стекла, и в детектор попадает новый фотон. Интересно, что сложение миллиардов маленьких стрелочек, отвечающих амплитуде рассеяния входящего фотона всеми электронами стекла, можно заменить сложением всего двух стрелок – для «передней поверхности» и «задней поверхности» – и получить тот же самый ответ. Давайте разберемся почему.
Чтобы с этой точки зрения разобраться в отражении света от стеклянной пластинки, надо принять во внимание временное измерение. Прежде, говоря о свете монохроматического источника, мы использовали вымышленные часы, запускаемые на время, пока летит фотон. Стрелка часов определяла поворот амплитуды для данного пути. В формуле Р(А – В) (для амплитуды попадания фотона из одной точки в другую) никакие повороты не упоминаются. Что произошло с часами? Что произошло с поворотами?
В первой лекции я просто сказал, что источник света является монохроматическим. Чтобы правильно разобраться в частичном отражении от пластинки, мы должны внимательно рассмотреть источник монохроматического света. Амплитуда излучения фотона источником, как правило, меняется со временем: со временем изменяется направление этой амплитуды. Источник белого света – смеси многих цветов – излучает фотоны хаотическим образом: направление амплитуды изменяется резко и нерегулярно, рывками. Но, конструируя монохроматический источник, мы делаем прибор, в котором все так тщательно устроено, что легко вычислить амплитуду излучения фотона в определенный момент времени: амплитуда вращается с постоянной скоростью, как стрелка часов. (На самом деле стрелка амплитуды вращается с той же скоростью, что и стрелка наших воображаемых часов, но в противоположном направлении – см. рис. 67.)
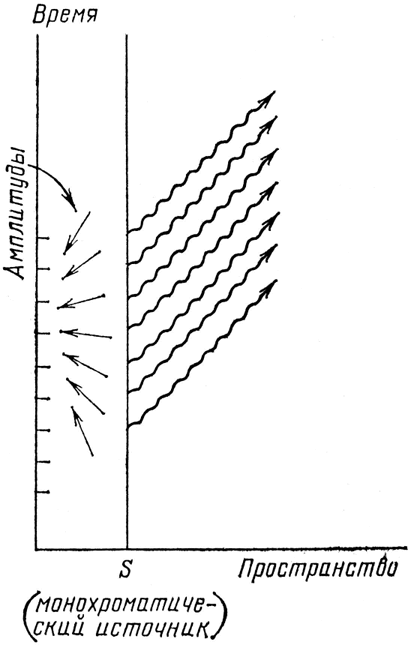
Рис. 67. Монохроматический источник света – это прекрасно сконструированный прибор, излучающий фотон легко пред-сказуемым способом: амплитуда излучения фотона в определенный момент поворачивается против часовой стрелки с течением времени. Поэтому амплитуда излучения фотона в более поздний момент имеет меньший угол поворота. Будем считать, что весь излучаемый источником свет распространяется со скоростью с (поскольку расстояния велики).
Скорость вращения зависит от цвета света: как и ранее, амплитуда синего источника вращается примерно в два раза быстрее, чем амплитуда красного источника. Итак, то, что мы использовали в качестве «воображаемых часов», было монохроматическим источником: на самом деле угол поворота амплитуды для данного пути зависит от того, в какой момент фотон вылетел из источника.
После излучения фотона стрелка не поворачивается, пока он летит из одной точки пространства-времени в другую. Хотя формула для Р(А – В) и утверждает, что у света есть амплитуда распространения со скоростью, отличной от с, в нашем эксперименте между источником и детектором относительно большое расстояние (по сравнению с атомными размерами), и сохраняется только вклад в длину Р(А – В), вносимый движением со скоростью с.
Чтобы заново начать рассматривать частичное отражение, прежде всего полностью определим наблюдаемое событие: детектор в А щелкает в определенный момент Т. Затем разделим стеклянную пластинку на несколько очень тонких слоев, скажем, шесть (см. рис. 68, а). Анализ, проведенный на второй лекции, показал, что практически весь свет отражается от середины зеркала, и хотя каждый электрон и рассеивает свет по всем направлениям, после суммирования всех стрелок для каждого слоя единственным местом, где стрелки взаимно не гасятся, окажется как раз середина слоя, где свет будет рассеиваться в одном из двух возможных направлений: назад к детектору или прямо в глубь стекла. Поэтому результирующая стрелка события может быть получена путем сложения шести стрелок, соответствующих рассеянию света в шести промежуточных точках X1…., Х6, расположенных друг над другом по всей толщине стекла.
Хорошо, давайте вычислим теперь стрелку для каждого из шести путей, по которым может лететь фотон, – через шесть точек X1…, Х6. Каждый путь состоит из четырех этапов. (Это значит, что надо будет перемножить четыре стрелки.)
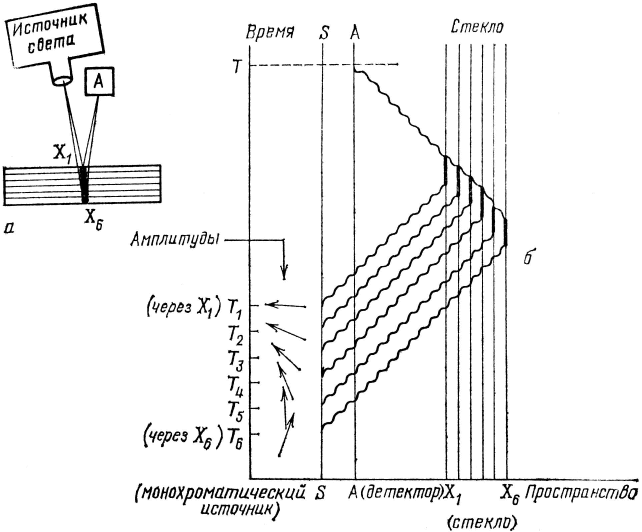
Рис. 68, а – б. Начнем новый анализ частичного отражения с того, что, разделив стеклянную пластинку на несколько слоев (в данном случае шесть), будем рассматривать различные пути, по которым свет может распространяться от источника к стеклу и назад, к детектору в точке А. Единственные существенные точки в стекле (где не гасятся амплитуды рассеяния) расположены в середине каждого слоя; реальное положение этих точек в глубине стекла показано на рис. а; на рис. б они изображены как вертикальные линии на пространственно-временном графике. Событие, вероятность которого мы рас-считываем, это срабатывание детектора в точке А в определенный момент времени Т. Поэтому событие изображается точкой (с координатами А и Т) на пространственно-временном графике. Каждый способ, которым может произойти событие, состоит из четырех последовательных этапов, поэтому надо перемножить четыре стрелки. Эти этапы показаны на рис. б: 1) в определенный момент фотон покидает источник (стрелки у отметок Т1…., Т6 изображают амплитуды этого события в шесть различных моментов времени); 2) фотон летит из источника в одну из точек стекла (шесть взаимоисключающих возможностей изображены в виде шести волнистых линий, идущих вправо вверх); 3) электрон в одной из точек рассеивает фотон (этот этап изображен в виде короткой жир-ной вертикальной линии); 4) новый фотон летит к детектору и попадает в него в условленное время Т (волнистая линия, направленная влево вверх). Амплитуды этапов 2, 3 и 4 одинаковы для всех шести возможностей, в то время как амплитуды первого шага различны по сравнению с фотоном, рассеянным на поверхности стекла (в точке Х1), фотон, рассеянный в глубине стекла, например в точке Х2, должен покинуть источник раньше, в момент времени Т2.
– Этап 1: В определенный момент источник излучает фотон.
– Этап 2: Фотон летит от источника к одной из точек в стекле.
– Этап 3: Фотон рассеивается электроном в этой точке.
– Этап 4: Новый фотон летит к детектору.
Мы будем считать, что амплитуды для этапов 2 и 4 (фотон летит к точке в стекле и от нее) имеют длину, равную 1, и нулевой угол поворота, поскольку можно предположить, что свет не теряется и не рассеивается между стеклом и детектором. Амплитуда этапа 3 (рассеяния фотона электроном) является константой – S (сжатие и поворот на некоторую величину) – и одинакова всюду внутри стекла. (Эта величина, как я отмечал ранее, различна для разных веществ. Для стекла поворот S равен 90°.) Следовательно, из четырех стрелок, которые нужно перемножить, только стрелка для этапа 1 – амплитуда излучения в определенный момент – будет разной для разных путей.
Момент, когда фотон должен вылететь из источника, чтобы достичь детектора А в момент Т (см. рис. 68, б), будет разным для шести различных путей. Фотон, рассеянный в точке Х2, должен быть излучен несколько раньше, чем фотон, рассеянный в Х1, поскольку его путь длиннее. Поэтому стрелка в Т2 повернута на несколько больший угол, чем в T1 – ведь пока время идет, амплитуда излучения фотона в определенный момент для монохроматического источника вращается против часовой стрелки. Это же относится к каждой стрелке вплоть до Т6: все шесть стрелок имеют одинаковую длину, но повернуты на разные углы, т. е. указывают в разных направлениях, поскольку относятся к фотону, излучаемому источником в разные моменты времени.
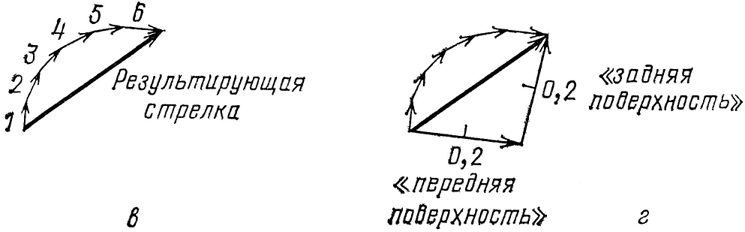
Рис. 68, в – г. Закончив умножать стрелки для каждой возможности, получим стрелки, показанные на рис. в. Они короче, чем стрелки на рис. б, каждая повернута на 90° (в соответствии с рассеивающими свойствами электронов стекла). При сложении эти шесть стрелок образуют дугу, результирующая стрелка является хордой этой дуги. Можно получить такую же результирующую стрелку, нарисовав две радиальные стрелки (на-правленные по радиусам дуги (см. рис. г) и «вычтя» одну из другой, т. е. повернув стрелку «передней поверхности» в обратную сторону и сложив со стрелкой «задней поверхности». Эта замена была использована для упрощения изложения в первой лекции.
Сжимая стрелку, относящуюся к T1, в число раз, предписанное этапами 2, 3 и 4, и поворачивая ее на 90°, предписанные этапом 3, получаем стрелку 1 (см. рис. 68, в). Следовательно, стрелки 1…., 6 имеют одинаковую (уменьшенную) длину и повернуты друг относительно друга на такой же угол, что и стрелки, характеризующие излучение фотона в Т1…., Т6.
Сложим теперь стрелки 1…., 6. Последовательно соединяя стрелки, получим нечто вроде дуги окружности. Результирующая стрелка служит хордой этой дуги. Длина результирующей стрелки возрастает по мере утолщения стекла: больше толщина стекла – больше слоев, больше стрелок – и получается большая дуга окружности. И так до тех пор, пока не получится половина окружности (результирующая стрелка в этом случае является диаметром). Затем, при нарастающей по-прежнему толщине стекла, длина результирующей стрелки начинает убывать, дуга превращается в полную окружность, и начинается новый период. Квадрат длины результирующей стрелки равен вероятности, которая за цикл колеблется в пределах от нуля до 16 %.
Для получения этого ответа можно применить математический трюк (см. рис. 68, г): соединив стрелками центр окружности с хвостом стрелки 1 и головой стрелки 6, получим две радиальные стрелки. Если повернуть первую из них на 180° и сложить со второй (т. е. «вычесть» первую из второй), получим прежнюю результирующую стрелку! Именно это я и делал на первой лекции: эти два радиуса и есть те две стрелки, которые, как я говорил, соответствуют отражению от «передней поверхности» и «задней поверхности». Каждая радиальная стрелка имеет хорошо известную нам длину 0,2.
Таким образом, мы можем правильно вычислить вероятность частичного отражения, предположив (ложно), что все отражение происходит только от передней и задней поверхности. При таком интуитивно простом расчете стрелки «передней поверхности» и «задней поверхности» – это дающие правильный ответ математические построения. В то же время проделанный нами только что анализ – в пространстве-времени со стрелками, образующими часть окружности, – более точно показывает, что происходит в действительности: частичное отражение – это рассеяние света электронами внутри стекла.
Теперь разберемся со светом, проходящим сквозь стекло. Во-первых, имеется некоторая амплитуда того, что фотон пролетит сквозь стекло, ни разу не столкнувшись с электронами (см. рис. 69, а). В смысле длины это самая важная стрелка. Но имеются еще шесть других возможных путей, которыми фотон может попасть в детектор под стеклом: фотон может столкнуться в точке X1, а новый фотон рассеется в В; фотон может столкнуться в точке Х2, а новый фотон рассеется в В, и т. д. Все шесть стрелок такой же длины, как и стрелки, образующие дугу в предыдущем примере: она определяется той же самой амплитудой рассеяния фотона в среде S. На этот раз все шесть стрелок направлены одинаково, так как все шесть путей с одним актом рассеяния имеют одинаковую длину. В таких прозрачных веществах, как стекло, эти малые стрелки направлены под прямым углом к основной стрелке. В результате сложения малых стрелок и основной стрелки получаем результирующую стрелку такой же длины, что и основная, но повернутую на небольшой угол. Чем толще стекло, тем больше будет малых стрелок и тем сильнее будет повернута результирующая стрелка. Так устроена фокусирующая линза; расположив на более коротких путях добавочные слои стекла, можно добиться того, чтобы результирующие стрелки для всех путей были направлены одинаково.
Эффект был бы таким же, если бы фотоны в стекле распространялись медленнее, чем в воздухе: результирующая стрелка сделала бы дополнительный поворот. Вот почему раньше я говорил, что свет в стекле (или воде) распространяется медленнее, чем в воздухе. В действительности «замедление» света объясняется добавочным вращением, связанным с рассеянием света атомами стекла (или воды). Величина этого добавочного поворота в данном веществе называется «показателем преломления вещества».
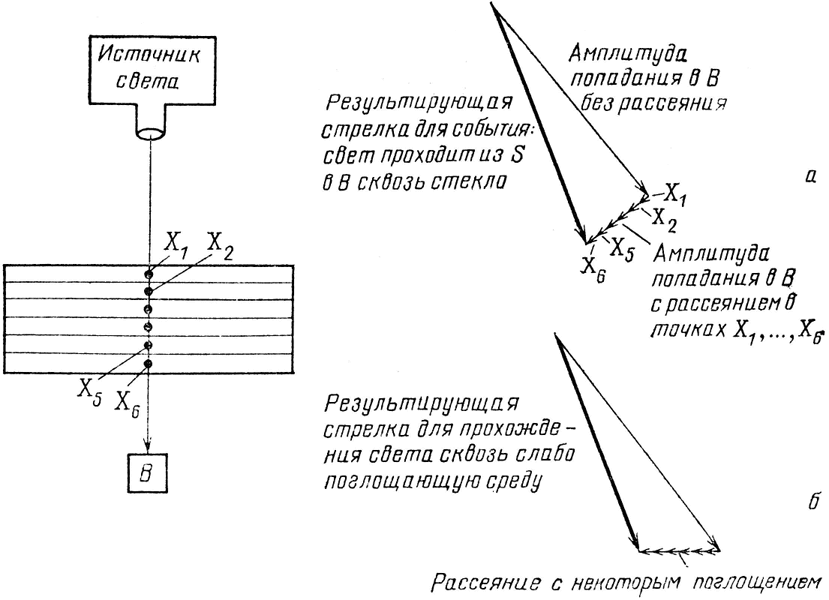
Рис. 69. Наибольший вклад в амплитуду прохождения света через стеклянную пластинку в детектор в точке В вносит часть, соответствующая отсутствию рассеяния на электронах стекла (а). К этой стрелке мы прибавляем шесть маленьких стрелок, отвечающих рассеянию света в каждом из слоев в точках X1…., Х6. Эти шесть стрелок имеют одинаковую длину (поскольку всюду внутри стекла амплитуда рассеяния одинакова), их направления совпадают (поскольку все пути от источника через любую из точек X к детектору имеют одинаковую длину). Сложив большую стрелку с маленькими, видим, что результирующая стрелка повернута сильнее, чем если бы свет распространялся прямо. По этой причине нам представляется, что путь через стекло занимает больше времени, чем через вакуум или воздух. Величина поворота результирующей стрелки, вызванного электронами вещества, называется «показателем преломления». В случае прозрачных веществ маленькие стрелки направлены под прямым углом к основной стрелке. (На самом деле при учете двойного и тройного рассеяния они несколько отклоняются, так что длина результирующей стрелки не превышает длины основной стрелки: Природа устроена так, что мы не можем получить на выходе из пластинки больше света, чем на входе.) В случае неполностью прозрачных (частично поглощающих свет) веществ маленькие стрелки направлены под тупым углом к основной стрелке. Поэтому результирующая стрелка получается значительно короче, чем ожидалось (б). Такая укороченная результирующая стрелка означает уменьшение вероятности прохождения фотона сквозь частично прозрачное вещество.
В случае поглощающих свет веществ малые стрелки направлены под тупым углом к основной стрелке (см. рис. 69, б). В итоге результирующая стрелка оказывается короче основной, что указывает на меньшую вероятность прохождения фотона сквозь частично прозрачное стекло, чем сквозь прозрачное.
Таким образом получается, что все явления, а также произвольные числа, о которых говорилось на первых двух лекциях, например, частичное отражение с амплитудой 0,2, «замедление» света в воде или в стекле, и т. д., более детально объясняются всего лишь тремя основными действиями – всего тремя, но объясняющими на самом деле и почти все остальное.
Трудно поверить, что почти все видимое бесконечное разнообразие Природы проистекает из монотонного повторения трех основных действий. Но это так. Я немного расскажу о том, как возникает это разнообразие.
Мы можем начать с фотонов (см. рис. 70). Какова вероятность того, что два фотона, выйдя из точек 1и 2 пространства-времени, попадут в два детектора в точках 3 и 4? Для осуществления этого события имеются два основных способа, и каждый состоит из двух независимых процессов: фотоны могут лететь прямо: Р(1–3)×Р(2–4) – или «крест-накрест»:
Р(1–4)×Р(2–3). Получающиеся таким образом амплитуды обеих возможностей складываются, и возникает (как мы видели на второй лекции) интерференция: длина результирующей стрелки меняется в зависимости от относительного положения пространственно-временных точек.
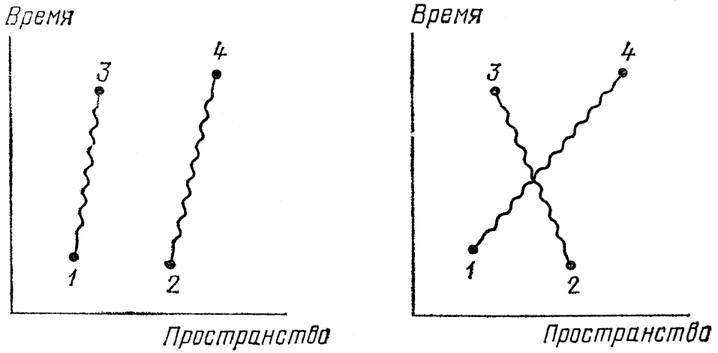
Рис. 70. Амплитуда попадания фотонов из точек 1 и 2 пространства-времени в точки 3 и 4может быть приближенно найдена, если рассмотреть два изображенных на рисунке основных способа осуществления этого события: Р(1–3)×Р(2–4) и Р(1–4)×Р(2–3). При изменении относительного положения точек 1, 2, 3 и 4 в различной степени проявляется интерференция.
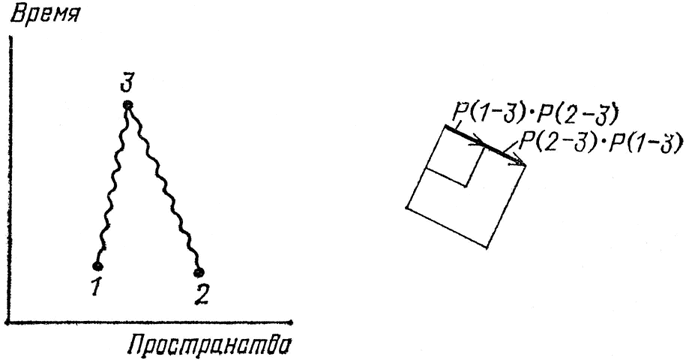
Рис. 71. Если совместить точки 4 и 3, две стрелки Р(1–3)×Р(2–3) и Р(2–3)×Р(1–3) окажутся одинаковыми как по дли-не, так и по направлению. При сложении они выстраиваются в одну линию и образуют стрелку удвоенной длины (квадрат которой при этом возрастает в четыре раза). Таким образом, фотоны стремятся попасть в одну пространственно-временную точку. При увеличении числа фотонов этот эффект усиливается. Он лежит в основе действия лазера.
Что произойдет, если мы совместим точки 3 и 4 в пространстве-времени (см. рис. 71)? Скажем, оба фотона попадают в точку 3. Посмотрим, как это скажется на вероятности события. В данном случае мы имеем Р(1–3)×Р(2–3) и Р(2–3)×P(1–3) – две одинаковые стрелки. При сложении их длина удвоится, что приведет к учетверению квадрата длины результирующей стрелки по сравнению с квадратом длины одной стрелки. Так как две стрелки одинаковы, они всегда «выстраиваются в одну линию». Другими словами, интерференция не флуктуирует при изменении положений точек 1 и 2, она всегда положительна. Если бы мы не учитывали такой всегда положительной интерференции двух фотонов, то мы ожидали бы, что вероятность возрастает в среднем в два раза. Вместо этого вероятность всегда возрастает в четыре раза. Когда мы имеем дело с большим числом фотонов, эта превосходящая наши ожидания вероятность возрастает еще сильнее.
Это приводит к целому ряду практических следствий. Можно сказать, что фотоны стремятся попасть в одинаковые условия или «состояния». («Состояние» – это определенная пространственная зависимость амплитуды нахождения фотона.) Вероятность того, что атом излучит фотон, возрастает, если уже имеются фотоны в таком состоянии, в котором они могут быть излучены данным атомом. Это явление, получившее название «вынужденного излучения», открыл Эйнштейн, когда, предложив фотонную модель света, он положил начало квантовой теории. Работа лазеров основана на этом явлении.
Такое же рассуждение применимо и к нашим фальшивым электронам со спином нуль. Но в реальном мире, где электроны поляризованы, происходит нечто совсем другое: две стрелки, Е(1–3)×Е(2–4) и Е(1–4)×Е(2–3), вычитаются одна из другой – т. е. перед сложением одна из них поворачивается на 180°. Если точки 3 и 4 совпадают, стрелки одинаковы как по длине, так и по направлению, и при вычитании взаимно уничтожаются (см. рис. 72). Это означает, что, в отличие от фотонов, электроны не любят попадать в одно место, они бегут друг от друга как от чумы. Два электрона с одинаковой поляризацией не могут оказаться в одной точке пространства-времени – это явление называется «принципом запрета».
Этот принцип запрета, оказывается, лежит в основе великого разнообразия химических свойств атомов. Один протон обменивается фотонами с танцующим вокруг него одним электроном – это атом водорода. Два протона одного ядра обмениваются фотонами с двумя электронами (поляризованными в противоположных направлениях) – это атом гелия. Видите ли, у химиков сложный способ счета: вместо того чтобы говорить «один, два, три, четыре, пять протонов», они говорят: «водород, гелий, литий, бериллий, бор».
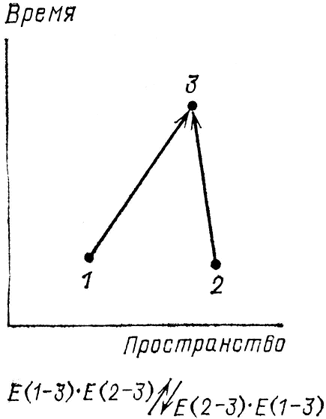
Рис. 72. Если два электрона (с одинаковой поляризацией) пытаются занять одну и ту же точку в пространстве-времени, интерференция всегда отрицательна. (Так проявляет-ся поляризация электронов.) Это значит, что две одинаковые стрелки Е(1–3)×Е(2–3) и Е(2–3)×Е(1–3) должны вычитаться друг из друга, в результате дли-на результирующей стрелки зануляется. Такое нежелание двух электронов занимать одно место в пространстве-времени называется «принципом запрета». Этим объясняется большое разнообразие атомов во Вселенной.
У электрона есть только два состояния поляризации, поэтому в атоме, где три протона ядра обмениваются фотонами с тремя электронами – он называется атомом лития – третий электрон расположен дальше от ядра, чем два других (занявших ближайшее возможное место), и реже обменивается фотонами. Такой электрон легко отрывается от своего ядра под действием фотонов других атомов. Большое число таких атомов, расположенных поблизости друг от друга, легко теряют свой собственный третий электрон, и получается целое море электронов, плавающих вокруг атомов. Если к этому морю электронов приложить слабую электрическую силу (фотоны), в нем образуется поток электронов – я описываю, как металлический литий проводит электрический ток. Водород и гелий не отдают свои электроны другим атомам. Они «изоляторы».
Все атомы – более ста их разновидностей – состоят из определенного числа протонов, которые обмениваются фотонами с таким же числом электронов. Способы расположения электронов сложны и обеспечивают громадное разнообразие свойств веществ: существуют металлы и изоляторы, газы и кристаллы. Одни вещества мягкие, другие твердые, одни окрашены, другие прозрачны. И все это колоссальное разнообразие, как из рога изобилия, вытекает из принципа запрета и повторения снова, и снова, и снова трех очень простых действий: Р(А – В), Е(А – В) и j. (Если бы у электронов не было поляризации, все атомы в мире имели бы очень похожие свойства: электроны собирались бы вместе, вблизи ядра своего атома, и не притягивались бы к другим атомам, образуя химические связи.)
Вам может показаться странным, каким образом такие простые действия могут создать столь сложный мир. Дело в том, что наблюдаемые нами явления представляют собой результат сложнейшего переплетения огромного числа обменов фотонами и интерференции. Знание трех фундаментальных действий – это только самое-самое начало в исследовании любой реальной ситуации, когда мы сталкиваемся с таким множеством обменов фотонами, что рассчитать их невозможно – надо приобрести опыт, чтобы научиться выделять наиболее важные возможности. Поэтому мы изобретаем такие понятия, как «показатель преломления» или «сжимаемость», или «валентность» – они помогают проводить расчеты приближенно, когда огромное количество деталей не просматривается. Это как игра в шахматы: одно дело знать основные правила, которые просты, и совсем другое – хорошо играть, тут надо понимать характер каждой позиции и природу разных положений, а это гораздо сложнее.
Разделы физики, изучающие вопросы типа «почему железо (с 26 протонами) является магнетиком, а медь (с 29 протонами) – нет» или «почему один газ прозрачен, а другой нет», называются «физикой твердого тела», «физикой жидкости» – в общем, настоящей физикой. Раздел физики, открывший три простых маленьких действия (самая простая часть), называется «фундаментальной физикой» – мы похитили это название, чтобы другие физики чувствовали себя неуютно! Совершенно очевидно, что самые интересные задачи, притом имеющие, конечно, наибольшее практическое значение, возникают сегодня в физике твердого тела. Но кто-то сказал, что нет ничего более практического, чем хорошая теория, а квантовая электродинамика – это определенно хорошая теория!
В заключение я хотел бы вернуться к числу 1,00115965221 – я говорил на первой лекции, что есть число, измеренное и вычисленное с очень большой точностью. Это число характеризует отклик электрона на внешнее магнитное поле – нечто, называемое «магнитным моментом». Когда Дирак впервые разрабатывал правила нахождения этого числа, он использовал формулу для Е(А – В) и получил очень простой ответ, равный 1 в нашей системе. Диаграмма, по которой магнитный момент электрона вычисляется в этом первом приближении, очень проста: электрон летит из точки в точку в пространстве-времени и взаимодействует с фотоном из магнита (см. рис. 73).
Впоследствии было обнаружено, что эта величина не равна 1, что она чуть больше – примерно 1,00116. Эта поправка была вычислена Швингером в 1948 г.; она равняется j×j, деленному на 2π, и обусловлена альтернативным способом попадания электрона из точки в точку: по пути электрон внезапно излучает фотон, а затем (о ужас!) его же и поглощает (см. рис. 74). Может быть, в этом и есть нечто «безнравственное», но электрон это делает! Чтобы вычислить стрелку для этого случая, мы должны рассчитать стрелки для всех точек пространства-времени, где фотон может быть излучен или поглощен. То есть появятся две дополнительных Е(А – В), одна Р(А – В) и два j, которые надо перемножить. Студенты учатся делать это простое вычисление на втором курсе, изучая элементарную квантовую электродинамику.
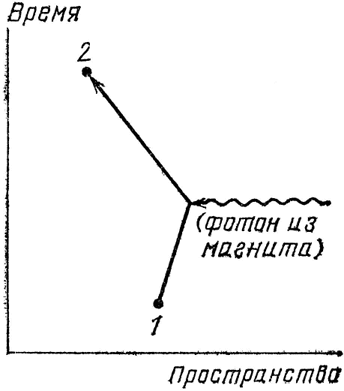
Рис. 73. Диаграмма для вычисления дираковского вклада в магнитный момент электрона очень проста. Величина, со-ответствующая этой диаграмме, принимается равной единице.
Но постойте! Эксперименты дают настолько точную картину поведения электрона, что в наших расчетах мы должны учитывать еще и другие возможности: все пути, которыми электрон попадает из точки в точку с четырьмя дополнительными взаимодействиями. На рис. 75 показаны три способа, которыми электрон может излучить и поглотить два фотона.
Имеется также и новая интересная возможность (показанная на рис. 75 справа): будучи излученным, фотон превращается в электрон-позитронную пару, которая – опять, если вы подавите свое «моральное» негодование, – аннигилирует и превращается в новый фотон, который затем поглощается электроном. Такую возможность тоже надо учитывать!
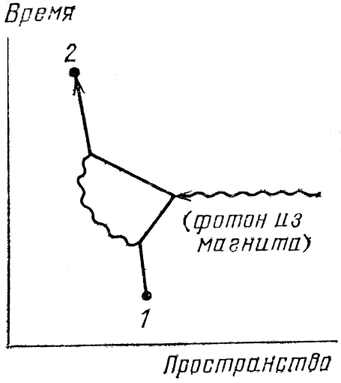
Рис. 74. Лабораторные эксперименты показывают, что настоящее значение магнитного момента электрона не равно, а несколько превышает 1. Это связано со следующей возможностью: электрон может испустить фотон, а затем поглотить его. Для описания этого процесса необходимы две дополнительных Е(А – В), одна Р(А – В) и два j. Швингер рассчитал, что учитывающая эту возможность поправка равна j×j/2π. Поскольку на опыте эта возможность неотличима от основного способа распространения электрона (см. рис. 73) – и там, и там электрон вылетает из точки 1 и попадает в точку 2 – стрелки обеих возможностей складываются, и возникает интерференция.
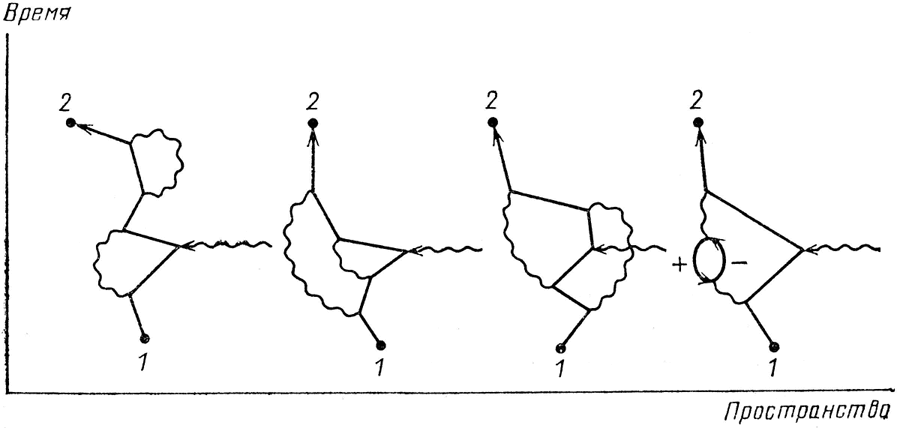
Рис. 75. При современной точности экспериментов необходимо учитывать диаграммы, содержащие четыре дополнительных взаимодействия (во всех возможных точках пространства-времени). Некоторые из таких диаграмм показаны на рисунке. Диаграмма справа содержит фотон, распадающийся на электрон-позитронную пару (см. рис. 64), аннигилирующую с образованием нового фотона, который и поглощается электроном.
Две группы физиков в течение двух лет независимо вычисляли этот следующий вклад и еще год искали ошибку: у экспериментаторов получалось несколько иное значение. Какое-то время казалось, что теория впервые не соответствует эксперименту. Но нет, ошибка была арифметической. Как могли две группы сделать одинаковую ошибку? Оказалось, что к концу работы обе группы сравнили свои расчеты и сгладили имевшиеся в них расхождения. Так что эти расчеты на самом деле не были совсем независимыми.
Поправка с шестью дополнительными j предполагает еще большее число способов осуществления события, и я нарисую некоторые из них (см. рис. 76). Двадцать лет потребовалось для того, чтобы получить теоретическое значение магнитного момента электрона с такой дополнительной точностью. Тем временем экспериментаторы выполнили еще более точные измерения и добавили несколько цифр к экспериментальному значению. И по-прежнему теория согласуется с экспериментом.
Итак, чтобы выполнить вычисления, мы рисуем эти диаграммы, выписываем, чему они соответствуют математически, и складываем амплитуды – все однозначно, как в поваренной книге. Поэтому все это может делать машина. Теперь, имея суперкомпьютеры, мы начали рассчитывать поправку с восемью дополнительными j. В настоящее время теоретическое значение равно 1,00115965246, экспериментальное – 1,00115965221 (±4 в последней цифре). Небольшая часть неопределенности теоретического значения (примерно 4 в последней цифре) связана с компьютерным округлением чисел; большая часть теоретической неопределенности (порядка 20) связана с тем, что значение j точно не известно. Поправка с восемью j состоит примерно из девяти сотен диаграмм, в математическом выражении для каждой из которых сто тысяч слагаемых. Это фантастические вычисления, и выполняются они прямо сейчас.
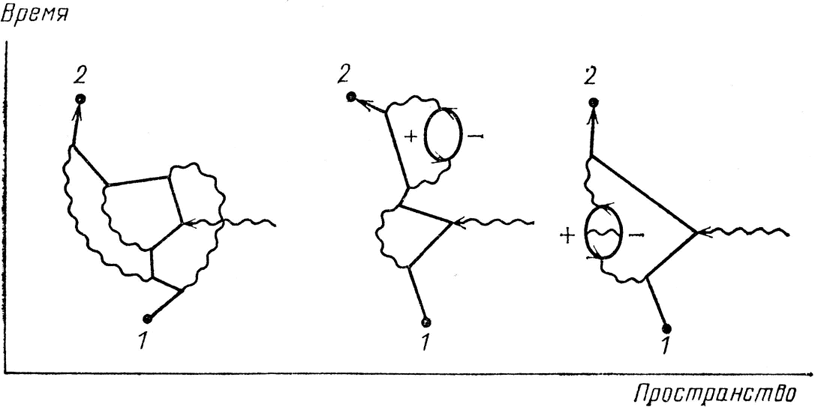
Рис. 76. И сейчас продолжаются вычисления, еще более повышающие точность теоретического значения. Следующий вклад в амплитуду, учитывающий все возможности с шестью взаимодействиями, состоит примерно из 70 диаграмм. Три из них показаны на рисунке. В 1983 г. теоретическое значение равнялось 1,00115965246 (с погрешностью около 20 в последних двух цифрах), экспериментальное – 1,00115965221 (с не-определенностью порядка 4 в последней цифре). Такая точность эквивалентна измерению расстояния от Лос-Анджелеса до Нью-Йорка (примерно 3000 миль) с точностью до толщины человеческого волоса.
Я уверен, что в ближайшие годы теоретическое и экспериментальное значения магнитного момента будут получены с точностью до еще большего числа знаков. Конечно, я не уверен, что два значения будут по-прежнему совпадать. Ничего нельзя сказать, пока не будут выполнены расчеты и эксперименты.
Итак, мы совершили полный круг и вернулись к числу, которое я выбрал в начале лекций, чтобы произвести на вас впечатление. Надеюсь, теперь вы гораздо лучше понимаете значение этого числа: по нему видно, с какой потрясающей точностью мы все время проверяем правильность этой странной теории – квантовой электродинамики.
Читая эти лекции, я получил истинное наслаждение, показывая, что столь точная теория создается ценой разрушения здравого смысла. Мы должны примириться с очень причудливыми явлениями: усилением и подавлением вероятностей, отражением света от всех частей зеркала, распространением света не по прямой и со скоростью, меньшей или большей обычной скорости света, движением электронов вспять во времени, внезапным распадом фотонов на электрон-позитронные пары, и т. д. Мы должны примириться со всем этим – чтобы осознать, какие действия Природы лежат на самом деле в основе практически всех наблюдаемых нами явлений.
Если не считать технических деталей, связанных с поляризацией, я описал вам лежащую в основе нашего понимания этих явлений концепцию. Мы рисуем амплитуду каждого из способов осуществления события, складываем эти амплитуды, в то время как в обычных условиях мы сложили бы вероятности, и умножаем амплитуды, в то время как в обычных условиях мы перемножили бы вероятности. На первых порах трудно думать обо всем на языке амплитуд из-за их абстрактности. Но человек вскоре привыкает к этому странному языку. Множество наблюдаемых нами ежедневно явлений основано всего лишь на трех основных действиях: одно описывается простой константой связи, два других – тесно связанными друг с другом функциями Р(А – В) и Е(А – В). Вот и все – и отсюда вытекают все остальные законы физики.
Однако, прежде чем закончить эту лекцию, мне хотелось бы сделать несколько дополнительных замечаний. Можно понять дух и характер квантовой электродинамики и не рассматривая технических деталей, связанных с поляризацией. Но я уверен, что вам будет как-то не по себе, если я не расскажу вам немного о том, что до сих пор опускал. Оказывается, фотоны бывают четырех видов, называемых «состояниями поляризации». Геометрически эти состояния связаны с пространственными и временным направлениями. Таким образом, имеются фотоны, поляризованные в Х-, Y-, Z- и Т-направлениях. (Возможно, вы где-нибудь слышали, что свет имеет только два состояния поляризации – например, фотон, летящий в Z-направлении, может быть поляризован только в Х– или Y-направлениях. Ну конечно, вы уже догадались: если фотон распространяется на большие расстояния и летит со скоростью света, амплитуды для Z– и Т-компонент взаимно уничтожаются. Но в атоме, когда электрон и протон обмениваются виртуальным фотоном, наиболее важна Г-компонента.)
Аналогично и электрон находится в одном из четырех состояний, которые тоже связаны с геометрией, но более тонким образом. Мы можем назвать эти состояния 1, 2, 3 и 4. Вычисление амплитуды попадания электрона из точки А пространства-времени в точку В при этом усложняется, так как мы теперь можем задавать такие вопросы: «Какова амплитуда того, что, вылетев из точки А в состоянии 2, электрон попадает в точку В в состоянии 3?» Шестнадцать возможных комбинаций – соответствующих четырем возможным начальным состояниям электрона в А и четырем возможным конечным состояниям в В – математически простым образом заключены в формуле для Е(А – В), о которой я вам уже рассказывал.
Для фотонов такой модификации не требуется. Фотон, поляризованный в Х-направлении в точке А, останется поляризованным в Х-направлении и в точке В, попав туда с амплитудой Р(А – В).
Благодаря поляризации происходит большое количество всевозможных взаимодействий. Например, мы можем спросить: «Какова амплитуда того, что электрон в состоянии 2 поглощает фотон, поляризованный в Х-направлении, и превращается в электрон в состоянии 3?» Не все возможные типы поляризованных электронов и фотонов взаимодействуют между собой, но те, что взаимодействуют, делают это с амплитудой j. (В некоторых случаях необходим еще дополнительный поворот стрелки на угол, кратный 90°.)
Существование состояний поляризации и природа взаимодействий могут быть очень изящно и красиво выведены из принципов квантовой электродинамики и двух дополнительных предположений: 1) результаты эксперимента не меняются, если экспериментальную установку повернуть на произвольный угол, и 2) они также не меняются, если установка движется в пространстве в космическом корабле с произвольной скоростью. (Это принцип относительности.) Этот изящный и общий анализ показывает, что каждая частица относится к тому или иному поляризационному классу. Так, мы говорим, что есть частицы со спином 0, спином ½, спином 1, спином 3/2, спином 2 и т. д. Частицы различных классов ведут себя по-разному. Частица со спином 0 – самая простая – имеет одну компоненту и вообще не поляризована. (Рассмотренные в этой лекции фальшивые фотон и электрон – это частицы со спином 0. Фундаментальные частицы со спином 0 до сих пор не обнаружены.) Настоящий электрон – это пример частицы со спином ½, а настоящий фотон – частицы со спином 1. Частицы со спином ½ и 1 имеют четыре компоненты. Частицы других классов имеют больше компонент; например, частицы со спином 2 имеют десять компонент.
Я сказал, что связь между относительностью и поляризацией проста и изящна, но не уверен, что смогу рассказать о ней просто и изящно! (Для этого потребовалась бы по крайней мере одна дополнительная лекция.) Хотя сложности, связанные с поляризацией, и не обязательно учитывать, чтобы понять дух и характер квантовой электродинамики, но для конкретных расчетов они, конечно, очень существенны и имеют глубокие последствия.
В этих лекциях мы сосредоточились на относительно простых взаимодействиях между электронами и фотонами на очень малых расстояниях, взаимодействиях, в которых участвует небольшое число частиц. Но я хотел бы сделать еще одно или два замечания о том, как эти взаимодействия проявляются на больших расстояниях, когда происходит обмен очень и очень большим числом фотонов. На таких больших расстояниях расчет стрелок сильно усложняется. Имеются, однако, не столь сложные для анализа ситуации. Например, бывают обстоятельства, когда амплитуда излучения фотона источником не зависит от того, излучались ли другие фотоны. Это происходит, если источник очень массивен (ядро атома) или если множество электронов будет двигаться единообразно (например, колебаться вверх и вниз в антенне радиопередатчика или вращаться по обмотке электромагнита). В этом случае излучается большое количество фотонов в совершенно одинаковых состояниях. Амплитуда поглощения фотона электроном в таких условиях не зависит от того, поглощал ли до этого фотоны этот или любой другой электрон. Поэтому все поведение и описывается просто амплитудой поглощения фотона электроном, зависящей только от положения электрона в пространстве и времени. Для описания такой ситуации физики пользуются обычными словами. Они говорят, что электрон движется во внешнем поле. Физики употребляют слово «поле» для обозначения величины, которая зависит от положения в пространстве и времени. Хороший пример поля – температура воздуха, она меняется в зависимости от того, где вы ее измеряете. С учетом поляризации у поля становится больше компонент. (А именно четыре – в соответствии с четырьмя амплитудами поглощения фотонов в разных состояниях поляризации (X, Y, Z, Т). Эти компоненты называются векторным и скалярным электромагнитными потенциалами. В классической физике из комбинаций потенциалов получаются более удобные компоненты, называемые электрическим и магнитным полями.)
Если электрическое и магнитное поля меняются достаточно медленно, амплитуда перемещения электрона на большие расстояния зависит от траектории его полета. Как мы видели ранее в случае со светом, наиболее важны те траектории, при малом изменении которых углы амплитуд практически не меняются. В результате получается, что частица не обязательно должна лететь по прямой линии.
Все это возвращает нас к классической физике, в которой предполагается, что есть поля и что электроны движутся в них так, что некоторая величина принимает наименьшее значение. (Физики называют эту величину «действием» и формулируют этот закон как «принцип наименьшего действия».) Вот вам один пример того, как квантовая электродинамика объясняет макроскопические явления. Отсюда мы можем двигаться в разных направлениях, но нужно положить какие-то пределы нашим лекциям. Я хотел только напомнить вам, что и явления, наблюдаемые нами на больших масштабах, и странные процессы, наблюдаемые на малых масштабах, порождаются взаимодействием электронов и фотонов и в конечном счете описываются квантовой электродинамикой.
Назад: Лекция 2. Фотоны: частицы света
Дальше: Лекция 4. Нерешенные вопросы

