Книга: КЭД – странная теория света и вещества
Назад: Лекция 1. Введение
Дальше: Лекция 3. Электроны и их взаимодействия
Лекция 2. Фотоны: частицы света
Это вторая лекция цикла, посвященного квантовой электродинамике, и так как очевидно, что никого из вас не было на прошлой лекции (потому что я всех предупреждал, что никто ничего не поймет), я вкратце повторю основные положения первой лекции.
Мы говорили о свете. Первое важное свойство света заключается в том, что он состоит из частиц: когда очень слабый монохроматический свет (свет одного цвета) попадает в детектор, детектор щелкает с одинаковой громкостью и все реже и реже по мере того, как свет тускнеет.
Другое важное свойство света, обсуждавшееся в первой лекции, – это частичное отражение монохроматического света. От единственной поверхности стекла отражается в среднем 4 % всех попадающих на нее фотонов. Это уже неразрешимая загадка, так как невозможно предсказать, какие фотоны отразятся, а какие пройдут насквозь. Когда появляется вторая поверхность, результаты странные: вместо ожидаемых 8 % отражения от двух поверхностей частичное отражение то усиливается до 16 %, то совсем исчезает, в зависимости от толщины стекла.
Это странное явление частичного отражения от двух поверхностей может быть объяснено для интенсивного света волновой теорией, но волновая теория не может объяснить, каким образом детектор издает одинаково громкие щелчки, когда свет тускнеет. Квантовая электродинамика «разрешает» вопрос о корпускулярно-волновом дуализме света, утверждая, что свет состоит из частиц (как считал в свое время Ньютон). Но ценой этого великого продвижения науки стало отступление физики на позицию, где признается возможным только вычисление вероятности того, что фотон попадет в детектор, и не предлагается хорошей модели того, как это в действительности происходит.
В первой лекции я рассказал, каким образом физики вычисляют вероятность того или иного события. Они рисуют на листе бумаги стрелки в соответствии со следующими правилами:
– ВЕЛИКИЙ ПРИНЦИП. Вероятность события равна квадрату длины стрелки, называемой «амплитудой вероятности». Например, стрелка длиной 0,4 соответствует вероятности 0,16, или 16 %.
– ОБЩЕЕ ПРАВИЛО рисования стрелок, если событие может произойти разными способами: нарисовать стрелку для каждого способа и затем соединить стрелки («сложить» их), цепляя голову одной за хвост другой. «Результирующая стрелка» проводится от хвоста первой стрелки к голове последней. Квадрат результирующей стрелки дает вероятность всего события в целом.
Было также несколько специальных правил для проведения стрелок в случае частичного отражения от стекла (их можно найти на с. 36–39).
Все вышесказанное представляет собой беглый обзор первой лекции.
Теперь я хотел бы показать вам, как эта модель мира, так разительно отличающаяся от всего, с чем вы встречались до сих пор (что, возможно, вы надеетесь с ней никогда больше не встретиться), может объяснить все известные вам простые свойства света: когда свет отражается от зеркала, угол падения равен углу отражения; свет отклоняется, попадая из воздуха в воду; свет распространяется по прямой; линза фокусирует свет и т. д. Теория также описывает многие другие свойства света, с которыми вы, возможно, и не знакомы. Самая большая трудность, с которой я столкнулся во время подготовки этих лекций, состояла в том, чтобы устоять перед искушением объяснить все вещи, связанные со светом, которые вы так долго изучали в школе. Например, отклонение света в область тени – то, что называется дифракцией. Но так как большинство из вас не наблюдало внимательно этих явлений, я не буду их касаться. Однако я могу гарантировать (в противном случае примеры, которые я собираюсь продемонстрировать, вводили бы вас в заблуждение), что любое явление, связанное со светом, которое было тщательно изучено, можно объяснить квантовой электродинамикой; хотя я буду описывать только простейшие и самые известные явления.
Начнем с зеркала и с вопроса о том, как от него отражается свет (см. рис. 19). В точке S имеется источник, испускающий очень слабый свет одного цвета (возьмем опять красный цвет). Источник испускает каждый раз по одному фотону. В точку Р поставим фотоумножитель, чтобы детектировать фотоны. Поставим его на той же высоте, что и источник – будет проще рисовать стрелки, если все симметрично. Мы хотим вычислить вероятность того, что детектор щелкнет после вылета фотона из источника. Так как фотон может полететь прямо в детектор, поставим экран в Q, чтобы это предотвратить.
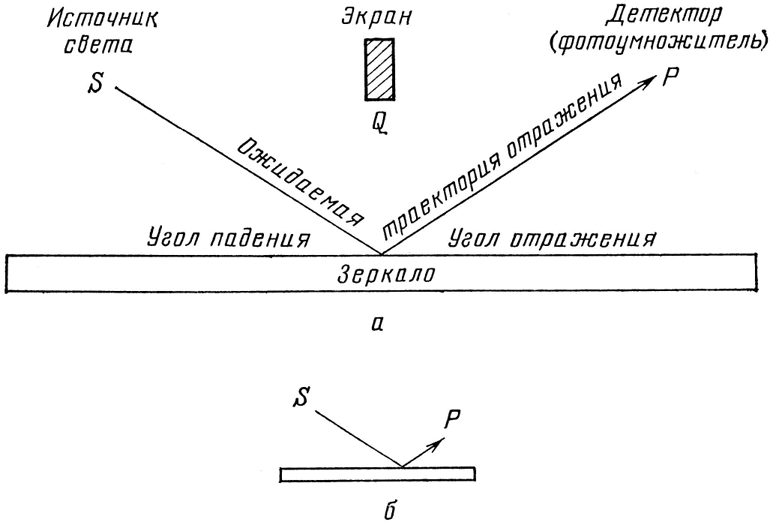
Рис. 19. Согласно классической картине мира зеркало будет отражать свет там, где угол падения равен углу отражения, даже если источник и детектор находятся на разных уровнях, как показано в случае б. (В дальнейшем на рисунках источник изображается буквой S (от source), фотоумножитель – Р (от photomultiplier). – Примеч. пер.)
Мы могли ожидать, что весь свет, достигающий детектора, должен отражаться от середины зеркала, так как именно в этом месте угол падения равен углу отражения. И кажется довольно очевидным, что части зеркала вблизи обоих его концов имеют такое же отношение к отражению, как к цене сыра, не так ли?
Хотя вы можете думать, что части зеркала вблизи обоих концов не имеют никакого отношения к отражению света, попадающего из источника в детектор, давайте посмотрим, что может сказать по этому поводу квантовая теория. Правило: вероятность того, что данное событие произойдет, равна квадрату результирующей стрелки, которую найдем, начертив стрелки для каждого способа, которым может произойти событие, и затем соединив («сложив») их. В эксперименте по измерению частичного отражения света от двух поверхностей было два пути, которыми фотон мог попасть из источника в детектор. В этом эксперименте (отражение от одной поверхности) фотон может лететь миллионом различных путей: он может попасть в левую часть зеркала в А или в В (например) и отскочить в детектор (см. рис. 20); он может отскочить от той части, от какой он, по вашему мнению, и должен отскакивать – от G; или он может попасть в правую часть зеркала в К или М и отскочить оттуда. Вы можете подумать, что я сошел с ума, так как в большинстве названных мною случаев угол падения не равен углу отражения. Но я не сошел с ума, потому что в действительности свет распространяется именно так! Как это может быть?
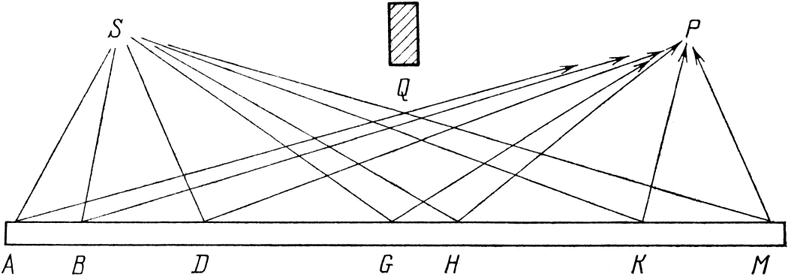
Рис. 20. Согласно квантовой картине мира свет имеет одинаковую амплитуду отразиться от любой части зеркала, от А до М
Чтобы упростить проблему, предположим, что зеркало представляет собой только длинную полоску слева направо, т. е. забудем на минуту, что зеркало имеет толщину и возвышается над бумагой (см. рис. 21). Хотя в действительности на этой зеркальной полоске имеется миллион мест, откуда мог бы отразиться фотон, приближенно допустим, временно разделив зеркало на конечное число маленьких квадратиков, что есть только одна траектория для каждого квадратика. Наш расчет будет более точным (но и производить его станет труднее) по мере того, как мы будем уменьшать квадратики и рассматривать большее количество траекторий.

Рис. 21. Чтобы легче было вычислить, где проходит свет, будем временно рассматривать только полоску зеркала, разделенную на квадратики. Каждому квадратику соответствует одна траектория. Это упрощение никоим образом не уводит в сторону от точного анализа ситуации.
Теперь нарисуем стрелку для каждого способа, которым свет может распространяться в этой ситуации. Каждая стрелка имеет определенную длину и направление. Рассмотрим сначала длину. Вы можете подумать, что стрелка, которую мы проведем для траектории, проходящей через середину зеркала G, будет самой длинной (так как кажется, что очень велика вероятность того, что фотон, попадающий в детектор, летит именно так), а стрелки для траекторий, проходящих через концы зеркала, будут очень короткими. Нет-нет, мы не должны устанавливать такие произвольные правила. А настоящее правило – и то, что на самом деле происходит, – гораздо проще: фотон, попадающий в детектор, имеет почти равные шансы попасть туда любым путем, так что все стрелки будут иметь почти одинаковую длину. (В действительности имеются очень небольшие различия в длине, связанные с различием в углах и расстояниях, но они настолько незначительны, что я их просто не буду учитывать.) Так что давайте условимся, что все нарисованные нами стрелки будут иметь некую произвольную одинаковую длину – я сделаю их очень короткими, потому что у нас будет очень много этих стрелок, изображающих множество возможных траекторий света (см. рис. 22).

Рис. 22. Каждый путь, по которому может идти свет, будет представлен в наших вычислениях стрелкой произвольной стандартной длины (как показано).
Хотя можно смело предположить, что все стрелки будут иметь почти одинаковую длину, они будут направлены по-разному, так как время пути по каждой траектории различно. Как вы помните из первой лекции, направление данной стрелки определяется конечным положением стрелки воображаемых часов, измеряющих время движения фотона по данной траектории. Ясно, что фотону, который попадает сначала в левый конец зеркала, а затем в детектор, требуется больше времени, чем фотону, попадающему в детектор из середины зеркала G (см. рис. 23). Или представьте на минуту, что вы очень торопитесь, а вам надо добежать от источника до зеркала, а оттуда попасть в детектор. Вы, конечно, понимаете, что глупо будет отправиться сначала в А, и потом проделывать весь долгий путь до детектора; гораздо быстрее будет коснуться зеркала где-нибудь в середине.
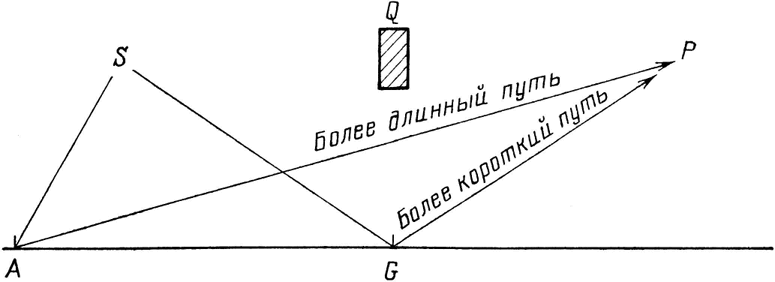
Рис. 23. В то время как длина стрелок существенно не меняется, направление будет различным, потому что фотону требуется разное время для движения по разным траекториям. Ясно, что время прохождения пути S – A – P больше, чем время про-хождения пути S – G – P.
Чтобы нам легче было вычислить направление каждой стрелки, я нарисую график прямо под зеркалом (см. рис. 24). Под каждой точкой зеркала, откуда мог отразиться свет, я отмечу по вертикали, сколько времени понадобилось бы свету, если бы он двигался именно по этой траектории. Чем больше времени понадобится, тем выше будут точки на графике. Начнем слева. Сначала фотону требуется довольно много времени, чтобы пролететь по траектории, имеющей точку отражения в А, так что поставим точку довольно высоко на графике. По мере продвижения к середине зеркала фотону требуется все меньше времени, чтобы проделать свой путь, поэтому ставим каждую следующую точку ниже предыдущей. После того как мы пройдем через центр, время полета фотона по каждой следующей, последовательно взятой траектории опять начнет увеличиваться, поэтому мы будем ставить наши точки соответственно все выше и выше. Для наглядности соединим точки: они образуют симметричную изогнутую кривую, которая начинается наверху, опускается и снова поднимается наверх.
Что это значит в смысле направления стрелок? Направление каждой отдельной стрелки соответствует тому, сколько времени понадобится фотону, чтобы попасть из источника в детектор по определенной траектории. Будем рисовать стрелки, начиная слева. Движение по траектории А требует больше всего времени, ее стрелка указывает в каком-то направлении (рис. 24). Стрелка для траектории В указывает в другом направлении, так как время движения по ней другое. В середине зеркала стрелки F, G и Н указывают почти в одном направлении, потому что время для них почти одинаково. Пройдя через центр зеркала, мы увидим, что каждая траектория с правой стороны зеркала соответствует траектории с точно таким же временем с левой стороны (это следствие того, что мы установили источник и детектор на одной высоте и точку G поставили точно в центре). Таким образом, стрелка, например, для траектории J направлена точно так же, как стрелка для траектории D.
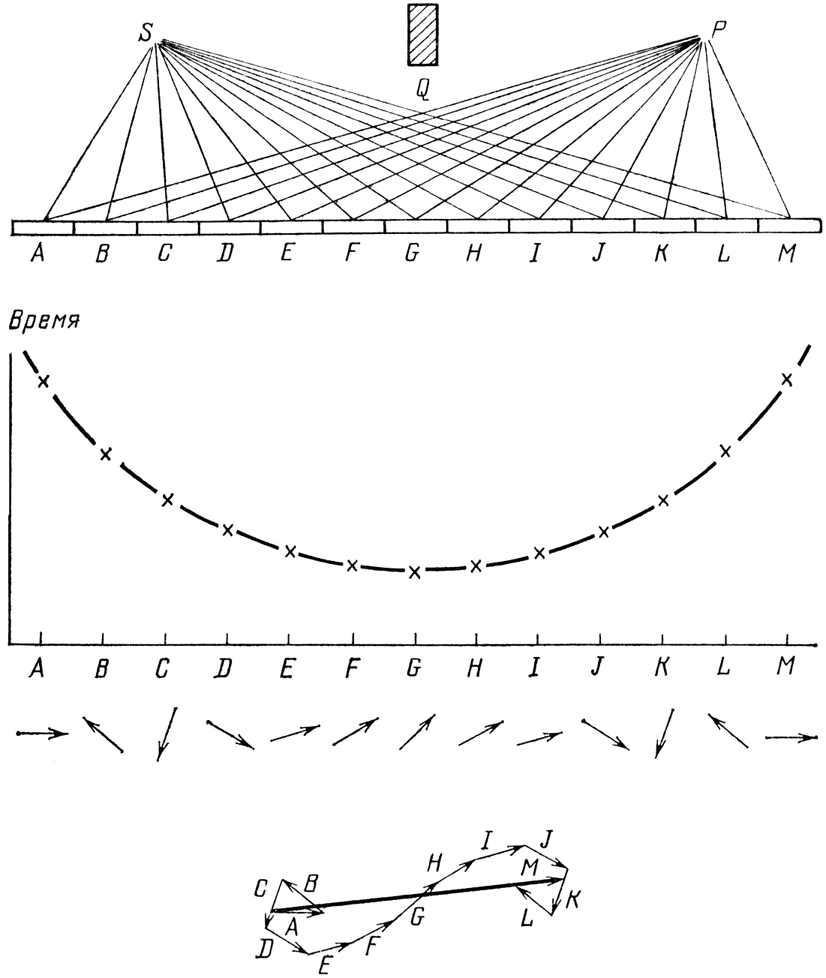
Рис. 24. Все пути, по которым мог бы пойти свет (в этом упрощенном случае), показаны наверху, а крестиками на графике (ниже) отмечено время, необходимое фотону для прохождения пути от источника до фотоумножителя через данную точку зеркала. Под графиком изображено направление каждой стрелки. А еще ниже – результат сложения всех стрелок. Очевидно, что основной вклад в результирующую стрелку вносят стрелки от Е до J, направленные почти одинаково, так как движение по соответствующим траекториям занимает почти одинаковое время. В том же месте общее время минимально. Поэтому приближенно можно допустить, что свет идет по тому пути, который занимает меньше всего времени.
Теперь давайте складывать стрелки (рис. 24). Начиная со стрелки А, мы цепляем стрелки одну к другой, головой к хвосту. Теперь представим себе, что мы отправились на прогулку, а каждая стрелка соответствует одному шагу. Сначала мы уйдем недалеко, так как направление движения сильно меняется от одного шага к другому. Но через некоторое время стрелки начинают показывать примерно в одном направлении, и мы продвигаемся. А к концу прогулки направление от одного шага к другому опять резко меняется, и мы опять топчемся на месте.
Все, что остается теперь сделать, – провести результирующую стрелку. Мы просто соединяем хвост первой стрелки с головой последней и видим, насколько мы продвинулись в нашей прогулке (рис. 24). И обратите внимание – мы получили довольно длинную результирующую стрелку! Квантовая электродинамика предсказывает, что свет действительно должен отражаться от зеркала!
Теперь давайте разберемся. Что определяет длину результирующей стрелки? Мы замечаем целый ряд вещей. Прежде всего концы зеркала не играют существенной роли: там стрелки кружат и никуда не приводят. Если бы я отрезал концы зеркала – те части, возня с которыми, как вы инстинктивно чувствовали, была пустой тратой времени, это едва ли повлияло бы на длину результирующей стрелки.
Итак, где же та часть зеркала, которая в основном и определяет длину результирующей стрелки? Это та часть, где все стрелки направлены почти в одну сторону, потому что у них почти одинаковое время. Посмотрев на график, изображающий время для каждой траектории, вы увидите, что время почти одинаково для двух соседних траекторий внизу кривой, там, где время наименьшее.
Итак, наименьшее время там, где оно почти одинаково для соседних траекторий, где стрелки указывают почти в одном направлении и при сложении дают значительную длину. Именно там определяется вероятность отражения фотона от зеркала. Вот почему в грубом приближении приемлемо упрощенное представление о мире, согласно которому свет идет там, где время наименьшее (и легко доказать, что там, где время наименьшее, угол падения равен углу отражения, но у меня нет времени, чтобы вам это показать).
Таким образом, квантовая электродинамика дала правильный ответ: именно середина зеркала важна для отражения, – но этот правильный результат получен за счет допущения, что свет отражается от всего зеркала и при помощи сложения множества стрелочек, которые были нужны только для того, чтобы взаимно уничтожиться. Все это может вам показаться пустой тратой времени – глупой игрой в математику. Это вовсе не похоже на настоящую физику – иметь дело с чем-то, что только исчезает!
Давайте при помощи другого эксперимента проверим идею, что отражение действительно происходит от всей поверхности зеркала. Во-первых, отсечем большую часть зеркала и оставим около четверти его с левой стороны. У нас все еще имеется довольно большой кусок зеркала, только находится он в другом месте. В предыдущем эксперименте стрелки с левой стороны зеркала указывали в самых разных направлениях из-за большой разницы во времени между соседними траекториями (рис. 24). В этом эксперименте я собираюсь произвести более детальный расчет, используя гораздо меньшие интервалы между траекториями в левой части зеркала – настолько маленькие, что между соседними путями не будет большого различия во времени (см. рис. 25). На этой более детальной иллюстрации видно, что одни стрелки указывают больше вправо, другие – больше влево. Если мы сложим все стрелки, то получим, по существу, кольцо и нулевую результирующую стрелку.
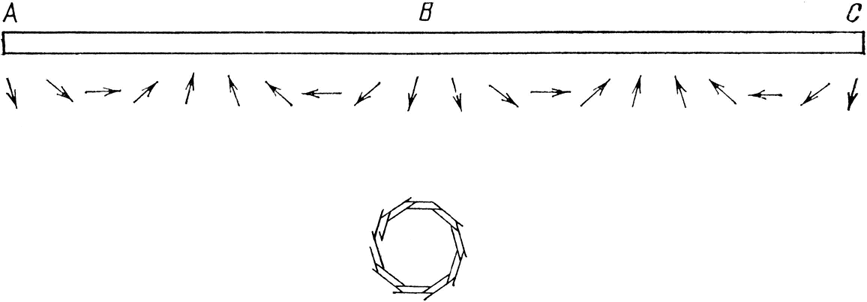
Рис. 25. Для проверки предположения, что в действительности отражение происходит и на концах зеркала (но просто нейтрализуется и сводится на нет), поместим большое зеркало в неподходящее для отражения из S в Р место (см. рис. 24). Это зеркало разделено на гораздо меньшие кусочки, так, чтобы разница во времени для двух соседних траекторий была невелика. Сложение всех стрелок ничего не дает: они идут по кругу, и сумма их ничтожна.
Но давайте предположим, что мы аккуратно процарапали зеркало в тех участках, где стрелки склоняются в одну какую-то сторону – допустим, влево, так что останутся только участки, где стрелки указывают в основном в другую сторону (см. рис. 26). Сложив стрелки, направленные более или менее вправо, мы получаем последовательность «прогибов» и довольно значительную результирующую стрелку – согласно теории у нас должно теперь быть сильное отражение! И действительно, оно есть – теория правильна! Такое зеркало называется дифракционной решеткой, и его действие похоже на волшебство.
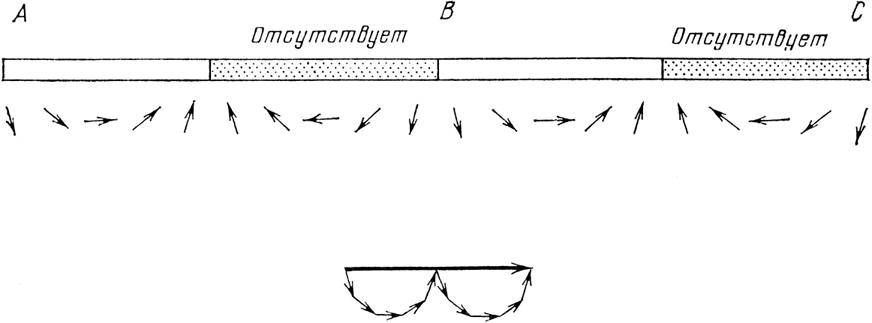
Рис. 26. Если сложить только стрелки, направленные в одну сторону (допустим, вправо) и пренебречь остальными (вытравив зеркало в этих местах), то от помещенного в неподходящее место зеркала отразится достаточное количество света. Такое протравленное зеркало называется дифракционной решеткой.
Не удивительно ли это – вы берете кусочек зеркала, где вы не ожидаете увидеть никакого отражения, сцарапываете часть его, и оно отражает!
Та решетка, которую я только что вам показал, была сделана специально для красного света. Она не действует, если свет синий; нам пришлось бы сделать другую, с вырезами, расположенными ближе друг к другу, потому что, как я говорил на первой лекции, стрелка часов крутится быстрее для синего фотона, чем для красного. Поэтому вырезы, рассчитанные специально на «красную» частоту вращения, приходятся на неправильные места для синего света; стрелки сбиваются, и решетка работает не очень хорошо. Но оказывается, что если мы передвинем фотоумножитель и поставим его под несколько иным углом, то решетка, сделанная для красного света, заработает для синего. Эта счастливая случайность является следствием геометрии (см. рис. 27).
Если вы будете светить на решетку белым светом, красный свет отразится в одном направлении, оранжевый в другом (чуть выше), за ним желтый, зеленый, голубой – все цвета радуги. Радужные цвета часто видны там, где рядом расположено много желобков – например, когда вы при ярком свете под правильным углом держите грампластинку (или, лучше, видеодиск). Возможно, вы видели замечательные серебристые значки (здесь, в солнечной Калифорнии, их особенно часто прикрепляют сзади на машины): когда машина едет, вы видите очень яркие цвета, переливающиеся от красного к синему. Теперь вы знаете, откуда берутся цвета: вы смотрите на решетку – зеркало, процарапанное как раз в нужных местах. Солнце – это источник света, а ваши глаза – детектор. Я мог бы продолжить и легко объяснить вам, как устроены лазеры и голограммы, но я знаю, что не все их видели, и к тому же есть много других вещей, о которых я должен рассказать.
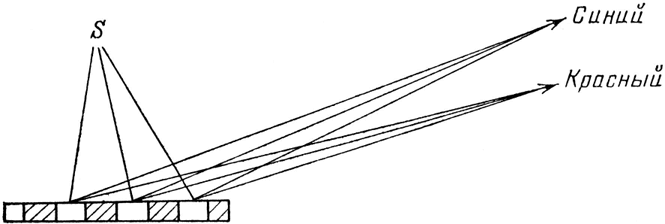
Рис. 27. Дифракционная решетка с бороздками на определен-ном расстоянии, которая годится для красного света, годится также и для других цветов, но для этого нужно поместить детектор в другое место. Таким образом, можно увидеть, как от рифленой поверхности – например от грампластинки – отражаются разные цвета в зависимости от угла зрения.
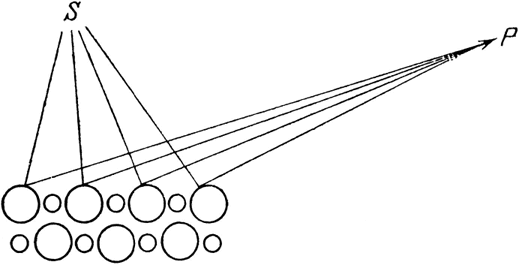
Рис. 28. Природа создала много типов дифракционных решеток в виде кристаллов. Кристалл соли отражает рентгеновские лучи (свет, для которого воображаемая стрелка часов движется чрезвычайно быстро, – скажем, в 10 000 раз быстрее, чем для видимого света) под различными углами, что дает возможность точно определить расположение отдельных атомов и расстояние между ними.
Итак, решетка показывает, что мы не можем игнорировать те части зеркала, которые на первый взгляд ничего не отражают; пойдя с зеркалом на некоторые хитрости, мы можем продемонстрировать реальность отражения от всех частей зеркала и вызвать поразительные оптические явления.
И что более важно, реальность отражения от всех частей зеркала показывает, что амплитуда – стрелка – существует для каждого способа, которым может произойти событие. И чтобы правильно вычислить вероятность события в различных обстоятельствах, мы должны складывать стрелки для каждого способа, каким могло бы произойти событие, а не только для способов, которые кажутся нам наиболее важными!
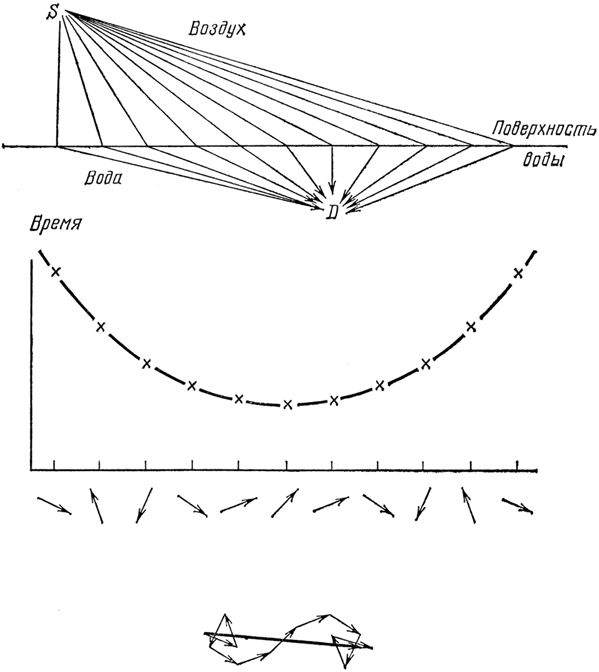
Рис. 29. Согласно квантовой теории свет может попасть из источника, находящегося в воздухе, в детектор, находящийся под водой, разными путями. Если упростить задачу, как в случае с зеркалом, можно нарисовать график, показывающий время каждой траектории, а под ним – направление каждой стрелки. И опять основной вклад в длину результирующей стрелки вносят те траектории, чьи стрелки указывают почти в одном направлении, так как у них почти одинаковое время, и снова для этих траекторий время будет наименьшим.
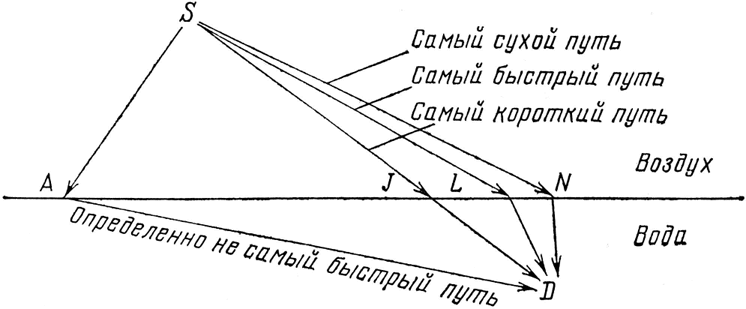
Рис. 30. Выбрать самый быстрый путь для света – все равно, что выбрать самый быстрый путь для спасателя, который сначала бежит, а затем плывет, чтобы спасти утопающего. На самом коротком пути надо слишком долго плыть; на пути, где меньше всего плыть, надо слишком долго бежать; самый быстрый путь – компромиссный между ними.
Теперь я хотел бы поговорить о более знакомых вещах, чем решетки, – о том, как свет переходит из воздуха в воду. На этот раз поместим фотоумножитель под водой – мы полагаем, что экспериментатор может это устроить! Источник света находится в воздухе в точке S, а детектор под водой в точке D (см. рис. 29). Как и прежде, мы хотим вычислить вероятность того, что фотон попадет из источника света в детектор. Чтобы это вычислить, мы должны принять во внимание все возможные пути, по которым мог идти свет. Каждый путь вносит свою стрелочку, и, как и в предыдущем примере, все стрелочки имеют почти одинаковую длину. Мы опять можем построить график времени движения фотона по каждой из возможных траекторий. График будет представлять собой кривую, очень похожую на ту, что мы начертили для света, отраженного от зеркала: она начинается высоко, опускается и опять поднимается. Наибольший вклад дают те места, где стрелки указывают почти в одном направлении (где время почти не меняется от траектории к траектории), что соответствует нижней части кривой. Там же будет и наименьшее время, так что все, что нам надо сделать, это найти, где время наименьшее. Получается так, что свет распространяется в воде как бы медленнее, чем в воздухе (почему, я объясню в следующей лекции), что делает пробег по воде, так сказать, более «дорогостоящим», чем пробег по воздуху. Нетрудно понять, движение по какому пути занимает меньше всего времени: представьте себе, что вы спасатель и сидите в точке S, а в точке D тонет красивая девушка (рис. 30). Вы бегаете по земле быстрее, чем плаваете по воде. Вопрос: где войти в воду, чтобы как можно скорее добраться до утопающей? Бежать к воде в точку А и потом чертовски быстро плыть? Нет, конечно. Но бежать прямо к несчастной и входить в воду в точке J – это тоже не самый быстрый путь. Конечно, в этих обстоятельствах спасателю глупо анализировать и вычислять, но маршрут, занимающий минимум времени, имеется, и его можно рассчитать: это компромисс между прямой дорогой через точку J и дорогой, где меньше всего воды, через точку N. Так же и со светом при вхождении в воду – траектория наименьшего времени проходит между точками J и N, скажем, в точке L.
Еще одно световое явление, о котором я хотел бы коротко упомянуть, это мираж. Когда едешь по сильно разогретому солнцем шоссе, то иногда кажется, что видишь на дороге лужи. На самом деле вы видите небо, а в нормальных условиях, если вы видите небо на дороге, то это потому, что дорога покрыта лужами (частичное отражение света от одной поверхности). Но как вы можете увидеть небо на дороге, если на ней нет воды? Надо вам сказать, что свет распространяется в прохладном воздухе медленнее, чем в теплом, и, чтобы увидеть мираж, наблюдатель должен находиться в прохладном воздухе, слой которого расположен над слоем горячего воздуха, непосредственно над поверхностью дороги (см. рис. 31). Каким образом можно смотреть вниз и видеть небо, будет понятно, если найти траекторию наименьшего времени. Займитесь этим дома – об этом занятно подумать и это очень легко выяснить.
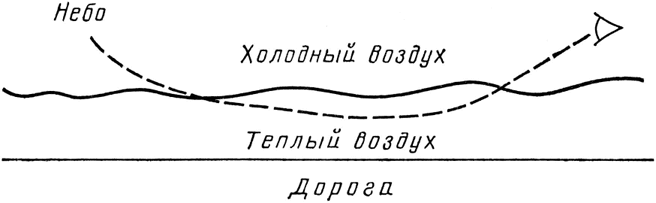
Рис. 31. Нахождение самого быстрого пути объясняет, как устроен мираж. В теплом воздухе свет распространяется быстрее, чем в холодном. Кусочек неба представляется лежащим на дороге, так как часть света от неба попадает в глаза, отразившись от дороги. Нам кажется, что мы видим небо на дороге только в одном случае, когда оно отражается в воде. Поэтому мираж кажется нам водой.
В рассмотренных нами примерах (свет отражается от зеркала и свет проходит через воздух, а затем через воду) я сделал некоторое допущение: для простоты я рисовал разные пути распространения света в виде ломаных линий – двух прямых, расположенных под углом друг к другу. Но мы не должны принимать как должное то, что свет распространяется по прямой в однородной среде, например в воде или в воздухе. Даже это объясняется общим принципом квантовой теории: вероятность события вычисляется при помощи сложения стрелок для всех способов, которыми могло произойти событие.
Итак, следующее, что я хочу показать вам, – это как, складывая стрелочки, увидеть, что свет распространяется по прямой. Поместим источник и фотоумножитель соответственно в точках S и Р (см. рис. 32) и рассмотрим все пути – самые разнообразные кривые, по которым свет может попадать из источника в детектор. Потом мы нарисуем маленькую стрелку для каждого пути – и мы хорошо усвоили наш урок!
Для каждой кривой, например для траектории А, существует соседняя траектория, которая намного прямее и ощутимо короче, – т. е. движение по ней занимает намного меньше времени. Но там, где траектории становятся почти прямыми – например в С, соседний, более прямой путь занимает почти такое же время. Вот там, где стрелки складываются, а не взаимно уничтожаются, там и идет свет.
Важно обратить внимание на следующее: единственная стрелка, соответствующая прямолинейной траектории через точку D (рис. 32), не может объяснить вероятности того, что свет попадет из источника в детектор по такому пути. Близкие, почти прямые траектории (через С и Е, например) также играют важную роль. Поэтому свет на самом деле распространяется не только по прямой. Он «обнюхивает» соседние траектории вокруг нее и использует небольшую часть ближайшего пространства. (По этой же причине и зеркало должно быть достаточного размера, чтобы нормально отражать: если зеркало слишком мало для пучка соседних траекторий, свет рассеивается во многих направлениях, куда бы вы ни поставили зеркало.)
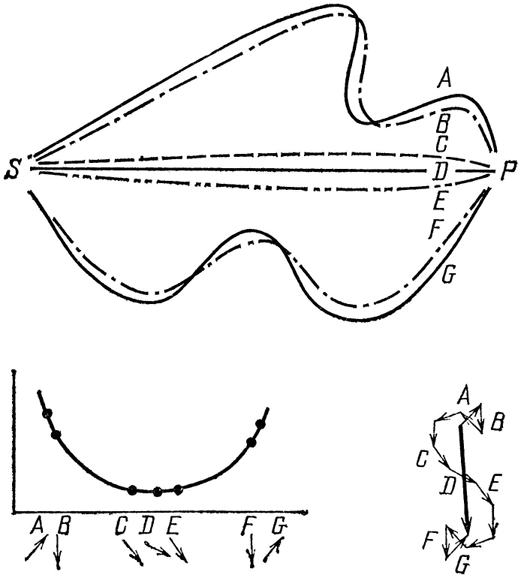
Рис. 32. При помощи квантовой теории можно объяснить, почему кажется, что свет распространяется по прямой. Изучение всех возможных траекторий показывает, что для каждой изо-гнутой траектории имеется близлежащая траектория, значительно более короткая, следовательно, требующая меньше времени (и существенно отличающаяся направлением стрелки). Только траектории, близкие к прямой траектории D, имеют стрелки, указывающие почти в одном направлении, так как у них почти одинаковое время. Важны только эти стрелки, так как из них складывается большая результирующая стрелка.
Давайте более тщательно исследуем этот пучок траекторий света, поместив источник в S,фотоумножитель в Р, а между ними – два кубика, чтобы траектории света не расходились слишком далеко (см. рис. 33). Теперь поставим второй фотоумножитель в Q, под Р, и опять будем считать, ради простоты, что свет может попасть из S в Q только по ломаным траекториям, состоящим из двух прямых отрезков. Что происходит? Когда промежуток между кубиками достаточно широк и может пропустить много соседних траекторий в Р и в Q, стрелки для траекторий, ведущих в Р, складываются (потому что все пути в Р занимают почти одинаковое время), а стрелки для траекторий, ведущих в Q, взаимно уничтожаются (потому что между этими траекториями имеется значительная разница во времени). Так что фотоумножитель в Q не щелкает.
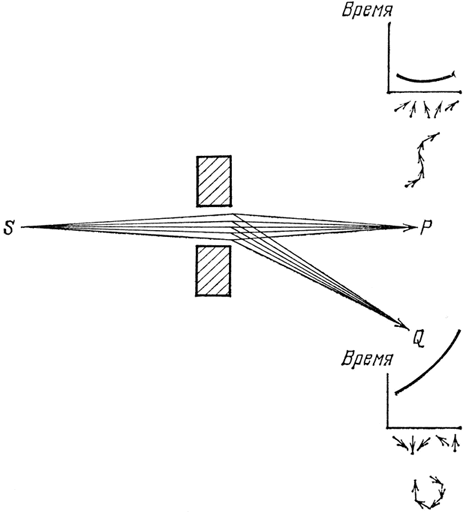
Рис. 33. Свет распространяется не только по прямой, но и по близлежащим траекториям. Когда два кубика раздвинуты на-столько, чтобы между ними поместились эти соседние траектории, фотоны, как им и положено, летят в Р и почти никогда не попадают в Q.
Но по мере сближения кубиков в какой-то момент детектор в Q начинает щелкать! Когда просвет почти закрыт и остается только несколько ближайших траекторий, стрелки траекторий, направленных в Q, также складываются, потому что и между ними почти не остается разницы во времени (см. рис. 34). Конечно, обе результирующие стрелки невелики, так что через такую маленькую дырочку ни в каком направлении не проникнет много света, но детектор в Q щелкает почти так же часто, как и в P?! Следовательно, когда вы стараетесь слишком сильно сжать пучок света, чтобы заставить его распространяться только по прямой, он отказывается подчиняться и начинает расширяться.
Итак, представление о том, что свет распространяется прямолинейно, – это приближенное представление, которым удобно пользоваться при описании явлений знакомого нам мира; оно подобно грубому приближению, согласно которому угол отражения от зеркала равен углу падения.
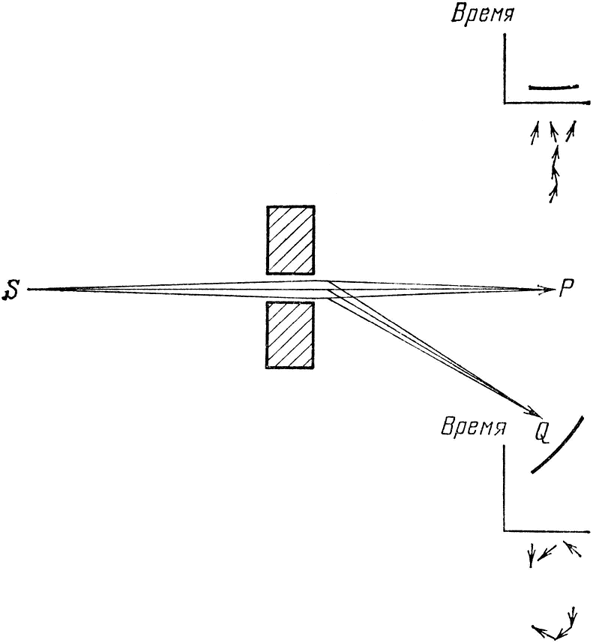
Рис. 34. Когда просвет сжат настолько, что остается только не-сколько траекторий, в Q попадет почти столько же просочившегося сквозь узкую щель света, сколько и в Р. Это связано с тем, что осталось слишком мало стрелок, соответствующих траекториям, ведущим в Q, чтобы они могли нейтрализовать друг друга.
Так же, как мы смогли при помощи некоторой хитрости заставить свет отражаться от зеркала под многими углами, мы можем похожим приемом заставить свет идти из одной точки в другую многими путями.
Прежде всего, чтобы упростить ситуацию, я нарисую вертикальную штриховую линию (см. рис. 35) между источником света и детектором (линия ничего не обозначает, это просто искусственная линия) и сообщу, что мы будем рассматривать только траектории, изображенные ломаными, которые состоят из двух отрезков. График, показывающий время для каждой траектории, выглядит так же, как и в случае с зеркалом (но на этот раз я поверну его боком): кривая начинается в А, наверху, затем она отклоняется влево, потому что траектории в середине короче и движение по ним занимает меньше времени. Наконец, кривая идет назад, вправо.
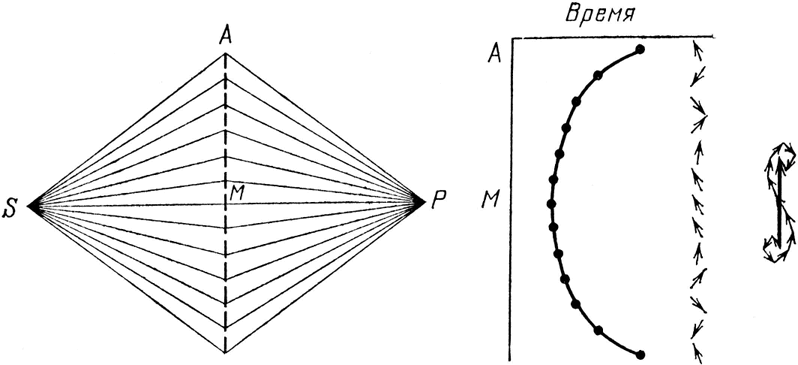
Рис. 35. Анализ всех возможных траекторий из S в Р упрощается, если учитывать только ломаные линии с одним изломом (лежащие в одной плоскости). Результат такой же, как и в более сложном, реальном случае: получается кривая времени с минимумом в том месте, где набегает наибольший вклад в результирующую стрелку.
Теперь немного развлечемся. Давайте «перехитрим свет» так, чтобы движение по всем траекториям занимало одинаковое время. Как это сделать? Каким образом самый короткий путь, через М, может занять точно такое же время, как и самый длинный путь, через А?
Мы знаем, что свет распространяется в воде медленнее, чем в воздухе; медленнее он распространяется и в стекле (с которым нам гораздо проще иметь дело!). Поэтому, поместив стекло нужной толщины на кратчайшем пути, проходящем через М, мы можем сделать так, что время для этой траектории будет в точности равно времени для траектории, проходящей через А. Траектории, соседние с М, чуть длиннее, и там не потребуется такое толстое стекло (см. рис. 36). Чем ближе мы подходим к А, тем тоньше должно быть стекло, которое надо ставить, чтобы замедлить свет. Если мы все тщательно рассчитаем и подберем для каждой траектории стекло нужной толщины, чтобы увеличить время движения, то все интервалы времени получатся одинаковыми. Когда мы нарисуем стрелки для каждого пути, по которому мог бы пойти свет, мы увидим, что нам удалось одинаково развернуть все стрелки – а ведь этих стрелочек миллионы – и конечный результат будет представлять собой необыкновенно длинную, просто громадную результирующую стрелку! Вы, конечно, догадались, что я описываю: это фокусирующая линза. Уравнивая все интервалы времени, мы можем фокусировать свет – мы можем получить очень высокую вероятность того, что свет попадет в определенную точку, и очень низкую – что он появится где-нибудь еще.
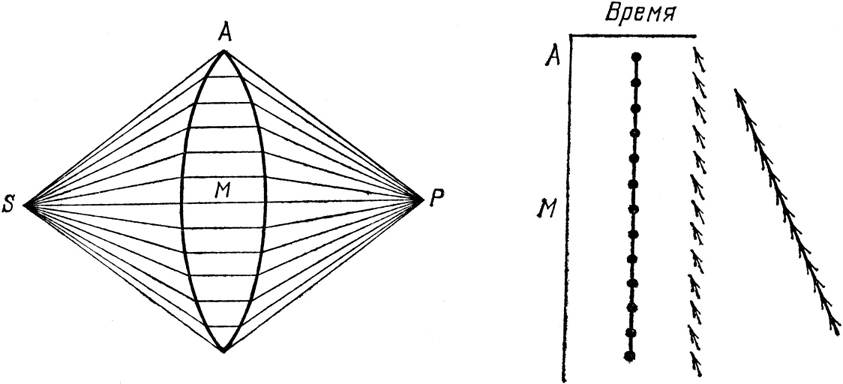
Рис. 36. Природу можно «обмануть», замедлив свет, идущий по более коротким траекториям. Для этого используется стекло такой толщины, чтобы движение по всем траекториям занимало одно и то же время. При этом все стрелки указывают в одном направлении и дают огромную результирующую стрелку – очень много света! Такое стекло, служащее для увеличения вероятности того, что свет из источника соберется в одной точке, называется фокусирующей линзой.
Я привел эти примеры, чтобы показать вам, как квантовая электродинамика, которая на первый взгляд кажется абсурдной, лишенной причинности, наглядного механизма и не имеющей отношения к реальности, тем не менее воспроизводит явления, с которыми вы хорошо знакомы: отражение света от зеркала, преломление света при переходе из воздуха в воду, фокусирование света линзой. Она также воспроизводит и другие явления, которых вы, вероятно, и не наблюдали – такие, как дифракция на решетке, и целый ряд других вещей. На самом деле теория успешно объясняет все световые явления.
Я показал вам, как вычислять вероятность события, которое может произойти различными взаимоисключающими способами: мы рисуем стрелку для каждого способа, которым может произойти событие, и складываем стрелки. «Сложение стрелок» означает, что стрелки соединяются так, что голова одной примыкает к хвосту другой, и проводится «результирующая стрелка». Квадрат полученной результирующей стрелки представляет собой вероятность события.
Чтобы вы смогли полнее почувствовать «вкус» квантовой теории, я хочу теперь показать вам, как физики вычисляют вероятность составных событий, т. е. таких событий, которые можно разбить на последовательность отдельных этапов, или таких, которые состоят из некоторого числа независимых событий.
Пример составного события можно получить, видоизменив наш первый эксперимент, в котором мы направляли красные фотоны на единственную поверхность стекла и измеряли частичное отражение. Вместо того чтобы помещать в А фотоумножитель (см. рис. 37), поставим туда экран с отверстием, через которое будут пролетать фотоны, достигшие точки А. Далее, поместим в В стеклянную пластинку, а в С фотоумножитель. Как вычислить вероятность того, что фотон попадет из источника в С?
Это событие можно рассматривать как последовательность двух этапов. Этап 1: фотон летит из источника в точку А, отразившись от единственной поверхности стекла. Этап 2: фотон летит из точки Ав фотоумножитель в С, отразившись от стеклянной пластинки в B. У каждого этапа имеется результирующая стрелка – «амплитуда» (я буду употреблять то одно, то другое слово), которую можно вычислить по уже известным нам правилам. Амплитуда первого этапа имеет длину 0,2 (квадрат ее равен 0,04, это вероятность отражения от единственной поверхности стекла) и направлена под некоторым углом – скажем, указывает на 2 часа (рис. 37).
Чтобы вычислить амплитуду второго этапа, мы временно поместим источник света в А и направим фотоны на стеклянную пластинку наверху. Нарисуем стрелки для отражений от передней и от задней поверхностей и сложим их – скажем, у нас получится результирующая стрелка длиной 0,3, указывающая на 5 часов.
Каким образом соединить обе стрелки, чтобы нарисовать амплитуду всего события в целом? Посмотрим на каждую стрелку по-новому: как на инструкцию, указывающую, во сколько раз сжиматьи на какой угол поворачивать.
В нашем примере первая амплитуда имеет длину 0,2 и повернута к 2 часам. Если мы начнем с «единичной стрелки» – стрелки длиной 1, направленной строго вверх, – мы должны сжать эту единичную стрелку от 1 до 0,2 и повернуть ее с 12 часов на 2 часа. Амплитуду второго этапа можно рассматривать как сжатие единичной стрелки от 1 до 0,3 и поворот с 12 часов на 5 часов.
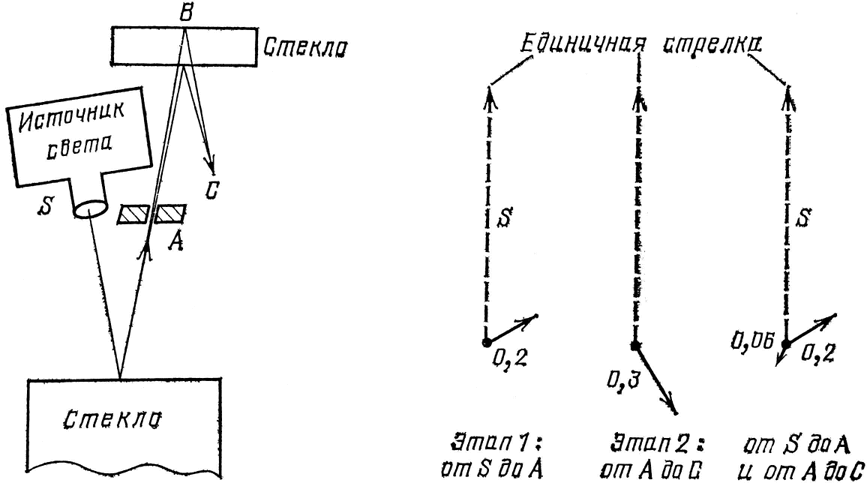
Рис. 37. Анализируя составное событие, можно разделить его на последовательные этапы. В этом примере траекторию фотона S – С можно разделить на два этапа: 1) фотон летит из S в А и 2) фотон летит из А в С. Можно анализировать каждый этап по отдельности и каждую стрелку рассматривать по-новому: как единичную стрелку (стрелку длиной 1, указывающую на 12 часов), подвергнутую сжатию и повороту. В этом примере сжатие и поворот для 1-го этапа составляют 0,2 и 2 часа; сжатие и поворот для 2-го этапа составляют 0,3 и 5 часов. Чтобы получить амплитуду двух последовательных этапов, мы последовательно сжимаем и поворачиваем. Сначала сжимаем единичную стрелку до 0,2 и поворачиваем на 2 часа, затем сжимаем полученную стрелку до 0,3 и поворачиваем на 5 часов (как если бы она была единичной стрелкой). В результате получаем стрелку длиной 0,06, повернутую на 7 часов. Эта последовательность поворотов и сжатий называется «умножением» стрелок.
Далее, чтобы соединить амплитуды обоих этапов, будем сжимать и поворачивать стрелки по очереди. Прежде всего сожмем единичную стрелку от 1 до 0,2 и повернем ее с 12 часов на 2 часа; затем мы сожмем стрелку еще сильней, от 0,2 до трех десятых этой величины, и повернем ее на 5 часов, т. е. мы повернем ее с 2 часов до 7 часов. В результате получится стрелка длиной 0,06, направленная на 7 часов. Она представляет вероятность, равную 0,06 в квадрате, т. е. 0,0036.
Внимательно рассмотрев стрелки, мы видим, что последовательное сжатие и вращение стрелок дает такой же результат, как сложение их углов (2 часа + 5 часов) и умножение их длин (0,2×0,3). Понять, почему мы складываем углы, просто: направление стрелки определяется поворотом воображаемой стрелки часов. Поэтому суммарный поворот для двух последовательных этапов просто равен сумме поворота на первом этапе и дополнительного поворота на втором этапе.
Вопрос о том, почему мы называем этот процесс «умножением стрелок», требует несколько более подробного объяснения, но это интересно. Давайте взглянем на умножение с точки зрения древних греков (это не имеет никакого отношения к лекции). Греки хотели пользоваться не только целыми числами, поэтому они изображали числа отрезками. Любое число можно представить в виде преобразования единичного отрезка – растягивая или сжимая его. Например, если отрезок Апредставляет собой единицу (см. рис. 38), то отрезок В представляет собой 2, а отрезок С – 3.
Теперь, как умножить 2 на 3? Мы проводим преобразования последовательно: взяв отрезок А в качестве единицы, мы удлиняем его в два раза, а затем еще в три раза (или в три раза, а затем еще в два раза – порядок умножения не имеет никакого значения). В результате получается отрезок D, длина которого представляет 6. А как умножить ½ на ⅓? Взяв в качестве единицы отрезок D, сожмем его до ½, а затем до ⅓ от этого. В результате получится отрезок А, представляющий 1/6.
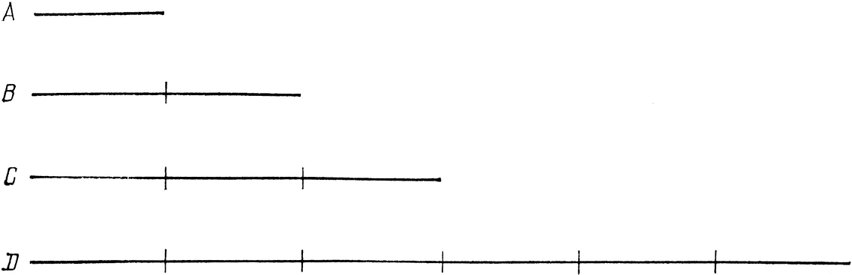
Рис. 38. Любое число может быть выражено в виде преобразования единичного отрезка посредством растяжения или сжатия. Если А – это 1, то B представляет собой 2 (растяжение), а С – 3 (растяжение). Умножение отрезков выполняется путем последовательных преобразований. Например, что значит умножить 3 на 2? Единичный отрезок растягивается в 3 раза, а затем еще в 2 раза, результат – растяжение в 6 раз (отрезок D). Если D – единичный отрезок, то отрезок С представляет собой 1/2 (сжатие), а отрезок В – 1/3 (сжатие), и умножение 1/2 на 1/3 означает, что единичный отрезок D сжат до 1/2, а затем до 1/3 от этого, давая ответ – сжатие до 1/6.
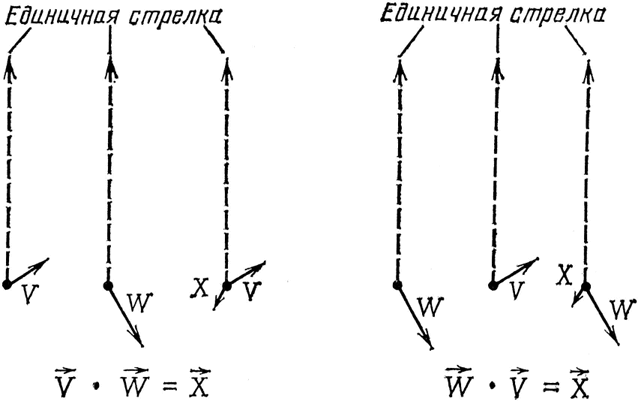
Рис. 39. Математики установили, что умножение стрелок может быть также выражено при помощи последовательных пре-образований (в нашем случае – сжатия и поворота) единичной стрелки. Как и при обычном умножении, от перемены мест сомножителей произведение не меняется. Чтобы получить ответ – стрелку X, вы можете умножать стрелку V на стрелку W или стрелку W на стрелку V.
Умножение стрелок устроено по этому же принципу (см. рис. 39). Мы последовательно проводим преобразование единичной стрелки – только преобразование стрелки включает теперь две операции – сжатие и поворот. Чтобы умножить стрелку W на стрелку V, мы сжимаем и поворачиваем стрелку настолько, насколько требует стрелка V, а затем настолько, насколько требует стрелка W – порядок опять не имеет никакого значения. Таким образом, умножение стрелок подчиняется тому же правилу последовательных преобразований, что и умножение обычных чисел.
Вернемся к первому эксперименту из первой лекции – частичному отражению света от единственной поверхности – имея в виду последовательность этапов (см. рис. 40). Мы можем разделить путь отражения на три этапа: 1) свет летит от источника к стеклу; 2) свет отражается от стекла; 3) свет летит от стекла к детектору. Каждый шаг можно рассматривать как сжатие и поворот единичной стрелки на определенную величину.
Вы помните, что в первой лекции мы не рассматривали все пути, которыми свет мог отразиться от стекла. Нам пришлось бы рисовать и складывать великое множество маленьких стрелочек. Чтобы избежать всех этих подробностей, я создал у вас впечатление, что свет попадает в определенную точку на поверхности стекла, – что он не расходится. На самом же деле по пути из одной точки к другой свет расходится (если только на его пути не встанет линза), и с этим связано некоторое сжатие единичной стрелки.
И пока я хотел бы продолжать придерживаться этого упрощенного взгляда, предполагающего, что свет не расходится. Поэтому мы можем пренебречь сжатием. Можно также предположить, что так как свет не расходится, каждый фотон, вылетевший из источника, завершит свой путь в А или в В.
Итак: на первом этапе отсутствует сжатие, но есть поворот единичной стрелки – он соответствует величине поворота воображаемой часовой стрелки за время движения фотона от источника до передней поверхности стекла. В нашем примере первому этапу соответствует стрелка единичной длины, направленная под некоторым углом, – допустим, указывающая на 5 часов.
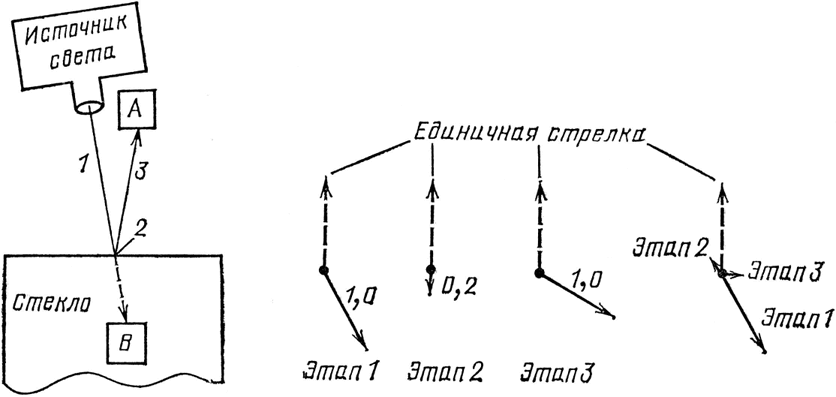
Рис. 40. Отражение от единственной поверхности можно разделить на три этапа, каждый со сжатием и/или поворотом единичной стрелки. Конечный результат – стрелка длиной 0,2, определенным образом направленная, – такой же, как и прежде, но наш метод анализа стал более подробным.
Второй этап – это отражение фотона от стекла. Здесь имеется заметное сжатие единичной стрелки – от 1 до 0,2 – и половина полного оборота: поворот на 6 часов. (Эти числа кажутся сейчас произвольными: они зависят от того, отражается ли свет от стекла или другого какого-нибудь вещества. В третьей лекции я их тоже объясню!) Таким образом, второму этапу соответствует амплитуда длиной 0,2, направленная на 6 часов (полуоборот).
Последний этап – это движение фотона от стекла к детектору. Здесь так же, как и на первом этапе, сжатие отсутствует, но есть поворот единичной стрелки – допустим, расстояние немного меньше, чем на первом этапе, и стрелка указывает на 4 часа.
Теперь «умножим» последовательно стрелки 1, 2 и 3 (сложим углы и перемножим длины). Конечный результат трех этапов – 1) поворота, 2) сжатия и полуоборота и 3) поворота – такой же, как и в первой лекции: суммарный поворот на первом и третьем этапах (5 часов + 4 часа) равен полученному нами в результате непрерывного движения часовой стрелки (9 часов); добавочный полуоборот второго этапа приводит к тому, что стрелка указывает в направлении, обратном часовой стрелке, как было и в первой лекции. А сжатие до 0,2 на втором этапе дает стрелку, квадрат которой соответствует 4 %-ному частичному отражению, наблюдавшемуся для единичной поверхности.
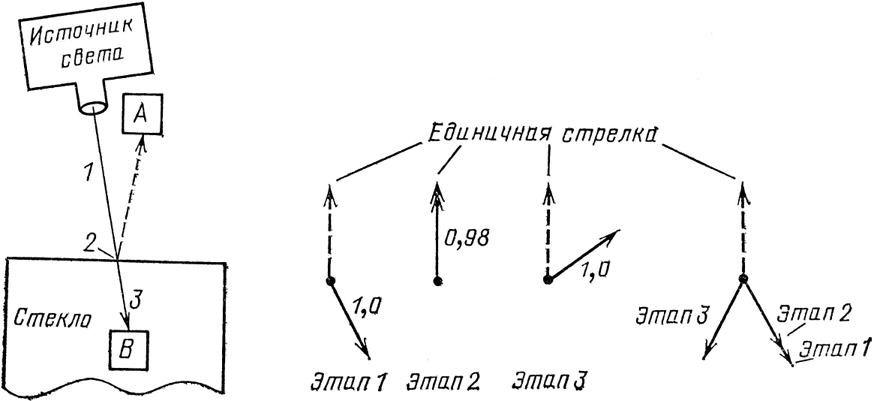
Рис. 41. Прохождение сквозь единственную поверхность также можно разделить на три этапа, со сжатием и/или поворотом на каждом этапе. Квадрат стрелки длиной 0,98 равен примерно 0,96, что дает 96 % вероятности прохождения (в сумме с 4 % вероятности отражения это дает все 100 % света).
В этом эксперименте возникает вопрос, который мы не рассматривали в первой лекции: что происходит с фотонами, летящими в В – с теми, что проникли сквозь поверхность стекла? Амплитуда того, что фотон попадет в В, должна иметь длину около 0,98, так как 0,98×0,98=0,9604, что достаточно близко к 96 %. Эту амплитуду также можно проанализировать, разложив ее на отдельные этапы (см. рис. 41).
Первый этап такой же, как для фотона, летящего в А: фотон летит из источника света к стеклу – единичная стрелка повернута на 5 часов.
На втором этапе фотон проходит сквозь поверхность стекла: при этом не происходит никакого поворота, а только небольшое сжатие – до 0,98.
Третий этап – прохождение фотона сквозь внутренний слой стекла – включает добавочный поворот без сжатия.
Конечный результат – это стрелка длиной 0,98, повернутая в некотором направлении, и ее квадрат соответствует вероятности того, что фотон попадет в В – 96 %.
Теперь давайте обратимся к частичному отражению от двух поверхностей. Отражение от передней поверхности будет таким же, как от единственной поверхности. Поэтому три этапа отражения от передней поверхности будут такими, как мы только что видели (см. рис. 40).
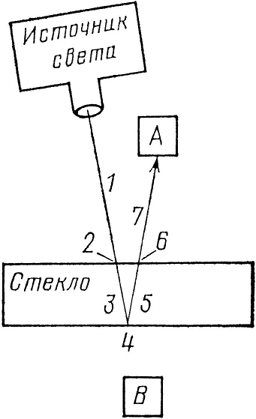
Рис. 42. Отражение от задней поверхности стеклянной пластинки можно разделить на семь этапов. На этапах 1,3, 5 и 7 происходит только поворот; на этапах 2 и 6 происходит сжатие до 0,98, а на этапе 4 – сжатие до 0,2. В итоге получается стрелка дли-ной 0,192, которую мы округляем до 0,2 (см. первую лекцию), повернутая на угол, равный полному повороту воображаемой часовой стрелки.
Отражение от задней поверхности можно разложить на семь этапов (см. рис. 42). Оно включает поворот, равный полному повороту часовой стрелки за время движения фотона по всему пути (этапы 1, 3, 5 и 7), сжатие до 0,2 (этап 4) и два сжатия до 0,98 (этапы 2 и 6). Результирующая стрелка указывает в том же направлении, что и прежде, но ее длина равна 0,98×0,2×0,98=0,192, что я в первой лекции округлил до 0,2.
Подводя итоги, сформулируем правила для отражения света от стекла и для прохождения света через стекло: 1) отражение из воздуха в воздух (от передней поверхности) сопряжено со сжатием до 0,2 и полуоборотом; 2) отражение от стекла в стекло (от внутренней поверхности) также включает сжатие до 0,2, но без поворота; 3) переход из воздуха в стекло или из стекла в воздух включает сжатие до 0,98 без поворота.
Вероятно, это уж слишком, но я не могу устоять перед искушением привести вам еще один интересный пример того, как ведет себя свет и как можно проанализировать его поведение, пользуясь правилами последовательных этапов. Поместим детектор под стеклом и рассмотрим вопрос, о котором мы не говорили в первой лекции, – о вероятности прохождения света через две поверхности стекла (см. рис. 43).
Вы, конечно, знаете ответ: вероятность того, что фотон попадет в В, равна просто 100 % за вычетом найденной раньше вероятности, что фотон попадет в А. Так, если мы получили, что вероятность попасть в А равна 7 %, то вероятность попасть в В равна 93 %. А так как вероятность для А меняется от 0 через 8 % до 16 % (для разных толщин стекла), то вероятность для В меняется от 100 % через 92 % до 84 %.
Это правильный ответ, но мы ожидаем, что все вероятности можно вычислять, возведя в квадрат результирующую стрелку. Как вычислить амплитуду пропускания света стеклянной пластинкой? И как ей удается таким именно образом менять свою длину, чтобы всегда соответствовать длине амплитуды А, так что вероятность для А и вероятность для В в сумме всегда дают 100 %? Давайте рассмотрим вопрос несколько подробнее.
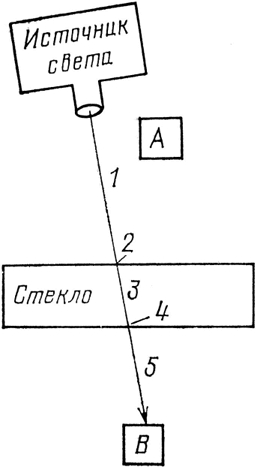
Рис. 43. Прохождение через две поверхности можно разделить на пять этапов. На этапе 2 единичная стрелка сжимается до 0,98, на этапе 4 стрел-ка длиной 0,98 сжимается еще раз до 0,98 (что дает примерно 0,96). На этапах 1, 3 и 5 происходит только поворот. В итоге квадрат стрелки длиной 0,96 будет равен примерно 0,92, что дает вероятность прохождения через две поверхности, равную 92 %. (Это соответствует 8 %-ному отражению, правильному лишь «дважды в сутки».) Когда толщина пластинки такова, что вероятность отражения равна 16 %, то в сумме с 92 % вероятности прохождения получается 108 %, т. е. мы учли 108 % света. В нашем анализе что-то неправильно!
Движение фотона от источника к детектору, находящемуся под стеклом, состоит из пяти этапов. Давайте сжимать и поворачивать единичную стрелку по мере продвижения.
Первые три этапа будут такими же, как в предыдущем примере: фотон летит из источника к стеклу (поворот, сжатия нет), фотон проходит сквозь переднюю поверхность (поворота нет, сжатие до 0,98); фотон проходит стекло (поворот, сжатия нет).
Четвертый этап – когда фотон проходит сквозь заднюю поверхность стекла – ничем не отличается от второго этапа в том, что касается поворотов и сжатия: поворота нет, а сжатие до 0,98 от 0,98, т. е. длина стрелки становится 0,96.
Наконец, пятый этап – фотон опять летит по воздуху в детектор – это значит, что происходит еще поворот, но без дальнейшего сжатия. В результате получаем стрелку длиной 0,96, указывающую в некотором направлении, заданном последовательными поворотами часовой стрелки.
Стрелка длиной 0,96 соответствует вероятности около 0,92 (0,96 в квадрате), а это значит, что в среднем 92 фотона из каждых 100, вылетевших из источника, попадают в В. Это также значит, что 8 % фотонов отражаются от обеих поверхностей и попадают в А. Но в первой лекции мы обнаружили, что 8 %-ное отражение от двух поверхностей бывает крайне редко («дважды в сутки») – что в действительности отражение от двух поверхностей флуктуирует периодически от нуля до 16 %, по мере постепенного утолщения слоя стекла. Что происходит, когда стекло имеет как раз такую толщину, чтобы частичное отражение составило 16 %? Из каждых 100 фотонов, вылетевших из источника, 16 попадают в А, а 92 – в В, что дает в сумме 108 % света – ужасно! Что-то неправильно.
Мы пренебрегли рассмотрением всех путей, по которым свет мог попасть в В. Например, он мог отразиться от задней поверхности и подняться сквозь стекло наверх, как будто бы направляясь в А, но затем отразиться от передней поверхности и опять попасть в В (см. рис. 44). Эта траектория состоит из девяти этапов. Посмотрим, что последовательно происходит с единичной стрелкой в то время, как свет проходит каждый этап (не беспокойтесь, это только сжатия и повороты!).
Первый этап – фотон летит по воздуху (поворот, сжатия нет). Второй этап – фотон проникает в стекло (поворота нет, сжатие до 0,98). Третий этап – фотон летит в стекле (поворот, сжатия нет). Четвертый этап – отражение от задней поверхности (поворота нет, сжатие до 0,2 от 0,98, т. е. до 0,196). Пятый этап – фотон в стекле возвращается наверх (поворот, сжатия нет). Шестой этап – фотон отскакивает от передней поверхности (это на самом деле «задняя» поверхность, так как фотон остается внутри стекла) (поворота нет, но сжатие до 0,2 от 0,196, т. е. до 0,0392). Седьмой этап – фотон возвращается вниз по стеклу (еще поворот, сжатия нет). Восьмой этап – фотон проходит сквозь заднюю поверхность (поворота нет, а сжатие до 0,98 от 0,0392, т. е. до 0,0384). Наконец, девятый этап – фотон проходит по воздуху в детектор (поворот, сжатия нет).
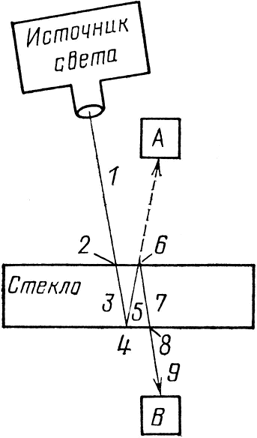
Рис. 44. Чтобы вычисление было более точным, надо рассмотреть и другой возможный способ прохождения света через две поверхности. Этот способ включает два сжатия до 0,98 (этапы 2 и 8) и два сжатия до 0,2 (этапы 4 и 6), в результате чего получается стрелка длиной 0,0384 (округляем до 0,04).
В результате всех этих сжатий и поворотов получаем амплитуду длиной 0,0384 – для всех практических вычислений можно считать ее примерно равной 0,04 – и повернутую на угол, соответствующий полному повороту часовой стрелки за время движения фотона по этой более длинной траектории. Эта стрелка соответствует второму пути, по которому свет может попасть из источника в В.Теперь у нас имеются два альтернативных варианта, поэтому, чтобы провести результирующую стрелку, мы должны сложить две стрелки: стрелку для более короткого пути, длиной 0,96, и стрелку для более длинного пути, длиной 0,04.
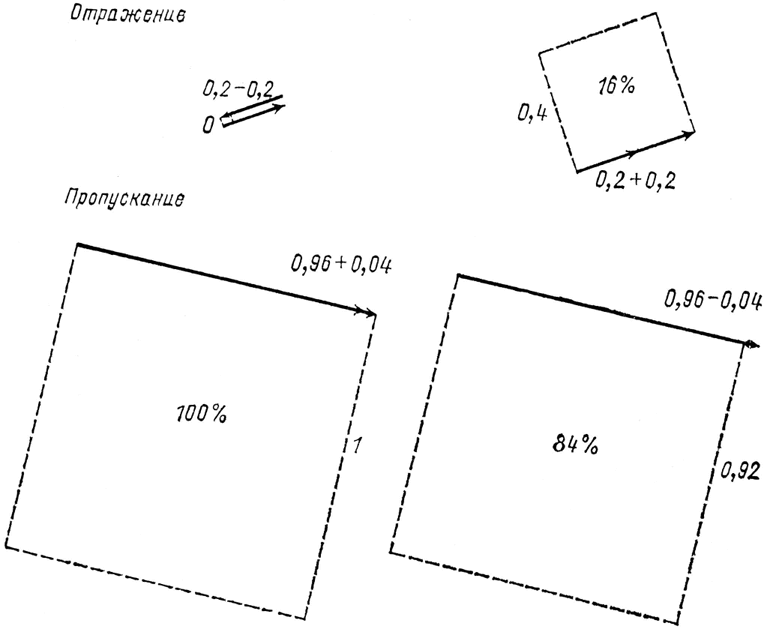
Рис. 45. Природа всегда следит за тем, чтобы были учтены все 100 % света. Когда толщина такова, что одинаково направлены стрелки пропускания, стрелки отражения противоположны друг другу; когда одинаково направлены стрелки отражения, стрелки пропускания противоположны друг другу.
Обычно две стрелки направлены по-разному, потому что изменение толщины стекла влечет за собой изменение направления стрелки длиной 0,04 относительно стрелки длиной 0,96. Но посмотрите, как хорошо все получается: дополнительные обороты, сделанные часовой стрелкой во время движения фотона на этапах 3 и 5 (по пути к А), в точности равны дополнительным оборотам, сделанным за время движения фотона на этапах 5 и 7 (по пути в В). Это значит, что, когда стрелки отражения взаимно уничтожаются, давая результирующую стрелку, соответствующую нулевому отражению, стрелки пропускания света усиливают друг друга, давая результирующую длиной 0,96+0,04, или 1. То есть, когда вероятность отражения равна нулю, вероятность пропускания света равна 100 % (см. рис. 45). А когда стрелки отражения усиливают друг друга, давая амплитуду 0,04, стрелки пропускания света направлены противоположно, что дает амплитуду длиной 0,96–0,04, или 0,92. Следовательно, когда отражение должно быть равно 16 %, пропускание света должно быть равно 84 % (0,92 в квадрате). Видите, как умно придумала Природа свои правила – они гарантируют нам, что мы всегда получим все 100 % учитываемых фотонов!
В заключение, прежде чем уйти, я хочу сообщить вам, что имеется дополнение к правилу о том, когда надо умножать стрелки: стрелки надо умножать не только, если событие состоит из последовательных этапов, но и если событие состоит из некоторого числа параллельных – независимых и, возможно, одновременных – явлений. Например, предположим, у нас есть два источника, Х и Y, и два детектора, А и В (см. рис. 47), и мы хотим вычислить вероятность следующего события: после того как Х и Y теряют по одному фотону, А и В приобретают по одному фотону. В этом примере фотоны летят в пространстве, чтобы попасть в детекторы – здесь нет ни отражения, ни пропускания, так что мне представляется удобный случай перестать, наконец, игнорировать тот факт, что свет расходится по мере распространения. Теперь представляю вам законченное правило для монохроматического света, распространяющегося в пространстве от одной точки до другой, – здесь нет никаких приближений и упрощений. Это все, что надо знать о монохроматическом свете, распространяющемся в пространстве (не считая поляризации): направление стрелки зависит от воображаемой часовой стрелки, делающей определенное количество оборотов на каждый дюйм пройденного пути (в зависимости от цвета фотона); длина стрелки обратно пропорциональна расстоянию, пройденному светом, – другими словами, стрелка сжимается по мере распространения света.
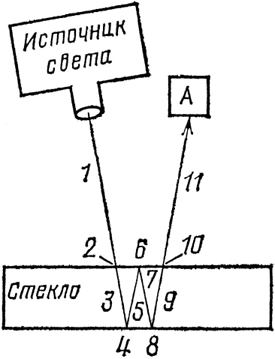
Рис. 46. Для более точных вычислений следует рассмотреть и другие возможные способы отражения света. На этом рисунке сжатия до 0,98 происходят на этапах 2 и 10; сжатия до 0,2 – на этапах 4, 6 и 8. В результате получается стрелка длиной при-мерно 0,008, которая соответствует еще одному возможному варианту отражения и которую поэтому надо сложить с другими отвечающими отражению стрелками (0,2 для перед-ней и 0,192 для задней поверхности).
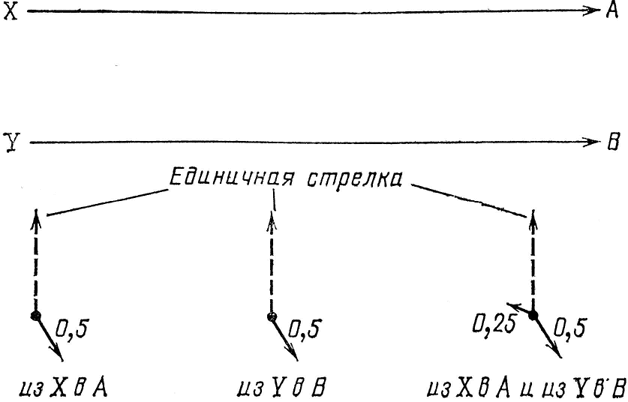
Рис. 47. Если один из способов, которым может произойти данное событие, зависит от некоторого количества независимых процессов, амплитуда этого способа вычисляется путем умножения стрелок для независимых процессов. В данном случае конечное событие таково: после того как источники Х и У каждый излучили по фотону, фотоумножители А и В издали по щелчку. Первый способ, каким могло произойти это со-бытие, состоит в том, что фотон из X мог попасть в А, а фотон из Y – в В (два независимых события). Чтобы вычислить вероятность этого «первого способа», надо умножить стрелки для каждого независимого события X – А и Y – B, получив таким образом амплитуду именно этого способа. (Продолжение анализа на рис. 48).
Предположим, стрелка X – А имеет длину 0,5 и указывает на 5 часов так же, как и стрелка Y – В (см. рис. 47). Перемножив стрелки, получаем результирующую стрелку длиной 0,25 и направленную на 10 часов.
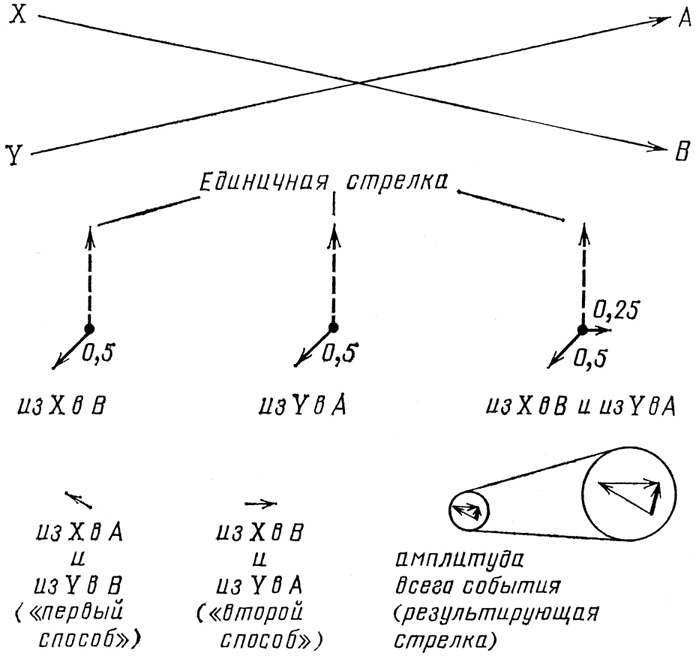
Рис. 48. Событие, обсуждаемое в подписи к рис. 47, могло бы происходить другим способом – фотоны летят из X в В и из Y в А. В этом случае все событие также зависело бы от двух независимых процессов, так что амплитуда этого «второго способа» вычисляется также путем умножения стрелок для независимых событий. Стрелки для «первого» и «второго» способов в конце концов складываются, давая результирующую стрел-ку всего события. Вероятность события всегда представляется единственной результирующей стрелкой – независимо от того, сколько стрелок было нарисовано, сложено и умножено, что-бы ее получить.
Но постойте! Это событие могло произойти другим способом: фотон из X мог отправиться в В, а фотон из Y – в А. Каждый из этих подпроцессов имеет свою амплитуду: надо также нарисовать и эти стрелки и перемножить их, чтобы получить амплитуду такого именно способа осуществления события (см. рис. 48). Так как величина сжатия, связанного с расстоянием, очень мала по сравнению с величиной поворота, стрелки X – В и Y – А имеют, по существу, такую же длину 0,5, как и стрелки X – А и Y – В, но направлены они будут совершенно по-другому: часовая стрелка делает 36 000 оборотов на один дюйм пробега красного света, поэтому даже маленькое изменение расстояния вызывает значительное изменение показаний стрелки.
Амплитуды для каждого способа, которым могло бы произойти событие, складываются и дают результирующую стрелку. Так как длины стрелок, по существу, одинаковы, имеется возможность того, что стрелки окажутся противоположно направленными и взаимно сократятся. Относительные направления двух стрелок можно менять, изменяя расстояние между источниками или детекторами: просто сдвигая или раздвигая детекторы, можно усилить или совсем уничтожить вероятность события, точно так же, как в случае частичного отражения от двух поверхностей.
В этом примере стрелки умножались, а затем складывались, и в итоге получалась результирующая стрелка (амплитуда события), квадрат длины которой равен вероятности события. Надо подчеркнуть, что независимо от того, сколько стрелок мы рисуем, складываем или умножаем, наша цель – получить единственную результирующую стрелку всего события. Студенты-физики поначалу часто совершают ошибки, так как упускают из виду этот важный момент. Они так долго трудятся над анализом событий, в которых участвует единственный фотон, что начинают считать, будто стрелка как-то связана с самим фотоном. Но эти стрелки представляют собой амплитуды вероятности, дающие при возведении их в квадрат вероятность всего события целиком.
В следующей лекции я начну упрощать и объяснять свойства вещества: покажу, откуда берется сжатие до 0,2, почему кажется, что свет проходит сквозь стекло или воду медленнее, чем сквозь воздух, и т. д. Ведь до сих пор я жульничал. На самом деле фотоны не отскакивают от поверхности стекла; они взаимодействуют с электронами внутри стекла. Я покажу вам, что фотоны в действительности только переходят от одного электрона к другому, и отражение и пропускание являются результатом того, что электрон захватывает фотон, потом, так сказать, «чешет в затылке» и испускает новый фотон. Это упрощение всего, о чем мы до сих пор говорили, очень приятно.
Назад: Лекция 1. Введение
Дальше: Лекция 3. Электроны и их взаимодействия

