12 Эволюционные игры
До сих пор мы изучали игры со множеством разных свойств — с одновременными и последовательными ходами; с нулевой и ненулевой суммой; стратегические ходы, позволяющие манипулировать правилами предстоящей игры; однократные, повторяющиеся и даже коллективные игры, в которые одновременно играет большое количество людей. Во всех этих случаях мы опирались на основополагающие правила традиционной теории игр, а именно — что у каждого игрока есть непротиворечивая система ценностей, что он может просчитать последствия своего стратегического выбора и делает выбор, максимально соответствующий его интересам. В процессе обсуждения, особенно при оценке эмпирических данных, мы признавали возможность того, что система ценностей игроков включает в себя заботу о других. А иногда, как при рассмотрении квантильного равновесия в , допускали, что игроки осознают вероятность ошибок. Но мы исходили из предположения, что каждый игрок делает осознанный и продуманный выбор из имеющихся в его распоряжении стратегий.
Однако появившиеся в последнее время теории ставят это предположение под сомнение. Наиболее обоснованная и убедительная критика исходит от психолога и лауреата Нобелевской премии по экономике 2002 года Даниэля Канемана. По его мнению, у людей есть две различные системы принятия решений. Система 1 — инстинктивная и быстрая, система 2 — расчетливая и медленная. Быстрая инстинктивная система может быть частично заложена в мозг человека в процессе эволюции, но также в значительной степени это результат обширного опыта и практики, что развивает интуицию. Эта система очень важна, поскольку экономит много умственных усилий и времени и часто первой применяется при принятии решения. При наличии достаточного количества времени и внимания ее может дополнить или вытеснить расчетливая и более медленная система. Когда инстинктивная система используется на все случаи жизни, накопленный опыт дополняет результат ее работы и может привести к постепенной модификации инстинкта.
Это подразумевает совершенно иной способ ведения и анализа игр. Игроки вступают в игру с инстинктивной системой 1 и разыгрывают стратегию, которую она им подсказывает, хотя эта стратегия может и не быть (или быть) оптимальной в данной ситуации. Положительный результат подкрепляет инстинкт, тогда как отрицательный способствует его постепенному изменению. Безусловно, результат зависит от того, какие стратегии применяет другой игрок или игроки, что зависит от состояния их инстинктивных систем, а это, в свою очередь, — от их опыта и т. д. Нам необходимо определить, куда ведет такой процесс интерактивной динамики инстинктов. В частности, мы должны выяснить, сходится ли он к выбору фиксированных стратегий, и если да, то как этот выбор согласуется с выбором, который бы предписала медленная система. Биологическая теория эволюции и эволюционной динамики предлагает один подход к этому анализу, его мы и опишем в данной главе.
1. Основные концепции
Биологическая теория эволюции основана на трех фундаментальных принципах: гетерогенность (неоднородность), приспособленность и отбор. Исходное положение состоит в том, что поведение животных в значительной мере генетически предопределено: комплекс из одного или более генов (генотип) обусловливает схему поведения (поведенческий фенотип). Естественное разнообразие генофонда обеспечивает гетерогенность фенотипов в популяции. Одни модели поведения в большей степени соответствуют сложившимся условиям, чем другие; успех фенотипа выражается в виде количественного показателя под названием приспособленность. Люди привыкли думать об успехе так, как о нем говорится в распространенной, но вводящей в заблуждение фразе «выживание наиболее приспособленных», тем не менее высший критерий биологической приспособленности — не выживание, а репродуктивный успех. Именно это позволяет животному передавать свои гены следующему поколению и сохранять свой фенотип. Затем более приспособленные фенотипы становятся относительно более многочисленными в следующем поколении, чем менее приспособленные. Именно этот динамический процесс отбора меняет комбинацию генотипов и фенотипов и, возможно, в конечном счете приведет к формированию устойчивого состояния.
Время от времени спонтанно возникают новые генетические мутации. Многие из них создают модели поведения (фенотипы), которые плохо сочетаются с окружающей средой и поэтому вымирают. Однако иногда мутация приводит к образованию нового фенотипа, более приспособленного к окружающей среде. Такой мутантный ген может захватить популяцию, то есть образовать значительную ее долю.
В любой момент времени популяция может содержать некоторые или все биологически возможные фенотипы. Доля более приспособленных фенотипов будет увеличиваться, некоторые неприспособленные могут исчезнуть, а фенотипы, в настоящий момент не входящие в состав данной популяции, могут попытаться ее захватить. Биологи называют конфигурацию популяции и ее текущих фенотипов эволюционно устойчивой, если ни один мутантный фенотип не может успешно ее захватить. Это статический критерий, но чаще применяется более динамический критерий: конфигурация популяции эволюционно устойчива, если она представляет собой единственно возможный результат динамического процесса отбора, начиная с любой произвольной комбинации фенотипов в данной популяции.
Приспособленность фенотипа зависит от взаимодействия отдельного организма с окружающей средой. Например, приспособленность определенной птицы зависит от аэродинамических характеристик ее крыльев, а также от всего комплекса разных генотипов, которые существуют в соответствующей среде: как аэродинамика крыльев птицы соотносится с аэродинамическими свойствами крыльев остальных птиц данного вида. Стало быть, приспособленность определенного животного (с его поведенческими характеристиками, такими как агрессивность и стадность) зависит от того, являются ли другие представители этого вида преимущественно агрессивными или пассивными, живут стаями или поодиночке и т. д. Для наших целей подобное взаимодействие между фенотипами в пределах одного вида — самый интересный аспект всей истории. Иногда представители одного вида взаимодействуют с представителями другого вида; тогда приспособленность определенного типа овец, например, может зависеть от качеств, доминирующих в местной популяции волков. Мы рассмотрим и этот тип взаимодействия, но только после анализа взаимодействия в пределах одного вида.
Все вышесказанное имеет свои параллели в теории игр. Поведение фенотипа можно рассматривать как стратегию животного в его взаимодействии с другими животными, например драться или спасаться бегством. Разница лишь в том, что выбор стратегии осуществляется не в результате целенаправленных расчетов, как в стандартной теории игр, а скорее, это генетически предопределенный вариант фенотипа. Взаимодействие обеспечивает фенотипам выигрыши. В биологии они отображают эволюционную или репродуктивную приспособленность; когда же мы используем эти идеи за пределами биологии, они могут иметь иной смысл, подразумевающий успех в социальных, политических и экономических играх.
Выигрыши или показатели приспособленности можно представить в виде таблицы выигрышей, точно так же, как и в обычной игре. В такой таблице все возможные фенотипы одного животного отображаются в строках матрицы, а другого животного — в столбцах матрицы. Если одновременно взаимодействуют больше животных (в биологии это называется игрой по всему полю), то выигрыши можно представить в виде функций, как в играх с коллективным действием из . В этой главе мы в основном будем рассматривать пары игроков, а случай со многими игроками кратко проанализируем в .
Поскольку популяция представляет собой комбинацию фенотипов, различные пары, выбранные из нее, используют во взаимодействии различные сочетания стратегий. Фактический количественный показатель приспособленности фенотипа — это средний выигрыш, который он получит во всех своих взаимодействиях с другими членами популяции. Животные с более высокой приспособленностью будут иметь более крупный эволюционный успех. Итогом динамики популяции станет ее эволюционно устойчивая конфигурация.
Биологи весьма успешно применили этот подход. Комбинации агрессивного и кооперативного поведения, местоположение гнездовий и многие другие явления, не поддающиеся более традиционному объяснению, можно рассматривать как устойчивые результаты эволюционного процесса отбора более приспособленных стратегий. Интересно, что биологи сформулировали идею эволюционных игр, воспользовавшись уже накопленными знаниями в области теории игр и ее терминами, но при этом изменив предположение об осознанных попытках обеспечить максимальное удовлетворение своих потребностей. Теперь специалисты по теории игр, в свою очередь, используют результаты исследований в области биологических эволюционных игр для обогащения своей области знаний.
Действительно, создается впечатление, что теория эволюционных игр — готовая концептуальная модель для изучения двух систем принятия решений Канемана. В других областях применения этой теории, не имеющих отношения к биологии, идею о том, что животные используют генетически заданные стратегии, можно интерпретировать более широко. Во взаимодействии между людьми стратегия может быть заложена в разуме человека по разным причинам, среди которых не только генетика, но и социализация (по всей вероятности, еще более важный фактор), культурное воспитание, образование или эмпирический опыт, основанный на прошлых событиях. Все это может охватывать инстинктивная, быстрая система 1 Канемана. Популяция может состоять из совокупности разных людей с разным происхождением или опытом, под влиянием которого они придерживаются различных стратегий системы 1. Так, некоторые политики стремятся соблюдать определенные моральные или этические нормы, даже рискуя успехом на выборах, тогда как другие озабочены только своим переизбранием. Точно так же некоторые компании могут гнаться исключительно за прибылью, тогда как другие преследуют социальные или экологические цели. В рассматриваемом контексте мы можем назвать все логически возможные стратегии, которые могут быть внедрены таким способом, фенотипом популяции игроков.
Из популяции с ее гетерогенностью встроенных стратегий случайным образом многократно выбираются пары фенотипов для взаимодействия (ведения игры) с другими представителями того же или иного «вида». В каждом взаимодействии выигрыш каждого игрока зависит от стратегий обоих; эта зависимость регулируется обычными «правилами игры» и отображается в таблице или дереве игры. Приспособленность конкретной стратегии определяется как ее совокупный или средний выигрыш, полученный в паре со всеми стратегиями данной популяции. У одних стратегий более высокий уровень приспособленности, чем у других, и в следующем поколении (то есть в следующем раунде игры) их используют больше игроков, что обеспечит их размножение. Стратегии с более низким уровнем приспособленности выберут меньше игроков, поэтому их число постепенно сойдет на нет и они исчезнут. Время от времени кто-то может экспериментировать или выбрать из множества логически возможных стратегий ту, которая еще не применялась. Эта ситуация соответствует появлению мутанта.
Хотя мы используем биологическую аналогию, причина увеличения количества более приспособленных стратегий и исчезновения менее приспособленных отличается от сугубо генетического механизма биологии: игроки, которые добились успеха в предыдущем раунде, передадут информацию друзьям и коллегам, играющим в следующем раунде, а игроки, плохо сыгравшие в предыдущем раунде, увидят, какие стратегии оказались более эффективными, и попытаются их имитировать. Другими словами, процесс целенаправленных размышлений и пересмотра предыдущих эмпирических правил происходит между раундами. Такие «социальные» и «обучающие» механизмы передачи информации гораздо важнее в большинстве стратегических игр, чем любая биологическая генетика; в действительности именно так подкрепляется ориентация законодателей на переизбрание и заинтересованность компаний в максимизации прибыли. И наконец, осознанное экспериментирование с новыми стратегиями замещает случайную мутацию в биологических играх. Постепенный процесс изменений с учетом исходов, опыта, наблюдений и экспериментов образует динамику расчетливой, медленной системы 2 Канемана.
Существует два типа эволюционно устойчивых конфигураций биологических игр. Во-первых, один фенотип может оказаться более приспособленным, чем другие, и популяция может состоять только из него. Такой эволюционно устойчивый результат обозначается термином мономорфизм, что означает «одна (моно) форма (морф)». В этом случае одна преобладающая стратегия называется эволюционно устойчивой стратегией (evolutionary stable strategy, ESS). Во-вторых, у двух или более фенотипов может быть одинаковый уровень приспособленности (и выше по сравнению с некоторыми другими генотипами, не принимающими участия в игре), поэтому они могут сосуществовать в определенных пропорциях. Тогда говорят, что популяция демонстрирует полиморфизм, то есть «множественность (поли) форм (морф)». Такое состояние будет устойчивым, если ни один новый фенотип или возможный мутант не сумеет достичь более высокого уровня приспособленности против данной популяции, чем уровень приспособленности тех типов, которые уже в ней присутствуют.
Полиморфизм очень близок к такому понятию теории игр, как смешанная стратегия. Однако есть одно важное отличие. Для получения полиморфизма ни одному отдельно взятому игроку не нужно придерживаться смешанной стратегии. Каждый член популяции может использовать чистую стратегию, но популяция в целом демонстрирует смешивание стратегий, поскольку различные игроки придерживаются различных чистых стратегий.
Вся эта структура (популяция, возможная комбинация фенотипов, таблица выигрышей при взаимодействии с другими фенотипами и правило эволюции соотношения фенотипов в популяции в зависимости от уровня их приспособленности) образует эволюционную игру. Эволюционно устойчивую конфигурацию популяции можно назвать равновесием в эволюционной игре.
В данной главе мы проанализируем некоторые из этих идей, как обычно, с помощью ряда иллюстративных примеров и начнем с симметричных игр, в которых два игрока находятся в одинаковых условиях. Скажем, два представителя одного вида соперничают друг с другом за пищу или самок или (в области социологии) два выборных чиновника конкурируют за право и дальше занимать соответствующую должность. В таблице выигрышей такой игры каждый игрок может быть выбран в качестве игрока, которому соответствуют строки, или в качестве игрока, которому соответствуют столбцы, — это не повлияет на исход игры.
2. Дилемма заключенных
Предположим, популяция состоит из двух фенотипов. Один включает игроков, которым от рождения свойственно стремление к сотрудничеству: они неизменно работают над достижением исхода, наилучшего для всех. Игроки другого типа не склонны к сотрудничеству и делают все исключительно ради себя. В качестве примера возьмем игру в ценообразование в ресторанах, описанную в и представленную в упрощенной версии в . Здесь мы рассмотрим более простую версию, в которой только два варианта выбора цен: наилучшая цена для обоих ресторанов 26 долларов и цена в случае равновесия Нэша 20 долларов. Ресторатор, настроенный сотрудничать, всегда будет выбирать 26 долларов, тогда как владелец ресторана, предпочитающий отказаться от сотрудничества, — 20 долларов. Выигрыши (прибыль) каждого типа в одной игре этой дискретной дилеммы показаны на рис. 12.1, где воспроизведена таблица с . Мы называем игроков просто Строка и Столбец, поскольку на месте каждого из них может быть любой ресторатор, который входит в состав популяции и которого выбирают случайным образом как конкурента другого случайно выбранного соперника.
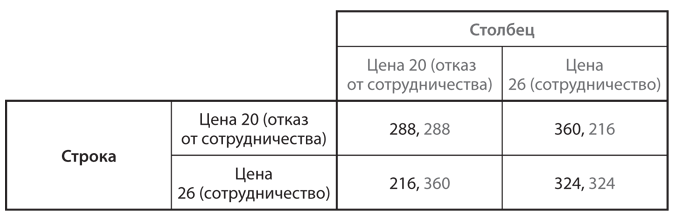
Рис. 12.1. Дилемма заключенных в контексте игры в ценообразование (выигрыши исчисляются в сотнях долларов в месяц)
Не забывайте, что в эволюционном сценарии ни у кого нет выбора между сотрудничеством и отказом от него; каждый «рождается» с тем или иным предопределенным качеством. Какое же качество будет более успешным (более приспособленным) в популяции?
Владелец ресторана, который относится к типу не склонных к сотрудничеству игроков, получает выигрыш 288 (28 800 долларов в месяц) в конкурентной борьбе с аналогичным типом и выигрыш 360 (36 000 долларов в месяц) — с типом, готовым сотрудничать. В свою очередь тип, готовый сотрудничать, получает 216 (21 600 долларов в месяц) в соперничестве с типом, не склонным к сотрудничеству, и 324 (32 400 долларов в месяц) — с аналогичным себе типом. Следовательно, тип, не расположенный к сотрудничеству, имеет более высокий ожидаемый выигрыш (а значит, и уровень приспособленности), чем тип, готовый к сотрудничеству, независимо от их соотношения в популяции.
Опишем эту ситуацию более формально. Пусть x — это доля готовых к сотрудничеству типов в популяции. Рассмотрим ее любого отдельно взятого члена, склонного к сотрудничеству. При случайном выборе вероятность того, что он встретит другого такого же представителя популяции (и получит выигрыш 324) равна x, а вероятность того, что он встретит игрока, не расположенного к сотрудничеству (и получит выигрыш 216), составляет (1 – x). Следовательно, среднестатистический ожидаемый выигрыш типа, склонного к сотрудничеству, равен 324x + 216(1 – x). Для противоположного типа вероятность встретить игрока, готового сотрудничать (и получить выигрыш 360), составляет x, а игрока аналогичного себе типа (выигрыш 288) — (1 – x). Таким образом, среднестатистический ожидаемый выигрыш типа, не склонного к сотрудничеству, составляет 360x + 288(1 – x). Очевидно, что при всех значениях x от 0 до 1 выполняется следующее условие:
360x + 288(1 – x) > 324x + 216(1 – x).
Стало быть, тип, не расположенный к сотрудничеству, имеет более высокий ожидаемый выигрыш и более высокий уровень приспособленности, чем тип, идущий на сотрудничество. Это обусловит увеличение доли этих типов (при этом снижается значение x) от поколения к поколению, пока вся популяция не будет состоять исключительно из типов, не склонных к сотрудничеству.
А что если популяция изначально состоит только из таких игроков? Тогда ни один (экспериментальный) мутант, готовый к сотрудничеству, не сможет в ней выжить и размножиться настолько, чтобы эту популяцию захватить. Иными словами, мутанты, расположенные к сотрудничеству, не добьются успеха в захвате популяции игроков, не склонных к нему. Даже при совсем малых значениях x (то есть когда доля игроков, готовых к сотрудничеству, очень мала) расположенные к сотрудничеству игроки остаются менее приспособленными по сравнению с оппонентами и их доля в популяции не увеличится, а будет сведена к нулю и мутантная линия исчезнет.
Наш анализ показывает, что у типа игроков, не расположенных к сотрудничеству, более высокий уровень приспособленности по сравнению с типом игроков, готовых к сотрудничеству, а также что популяция, состоящая только из игроков первого типа, не может быть захвачена мутантами. Таким образом, эволюционно устойчивая конфигурация популяции мономорфна и состоит из одной стратегии, или фенотипа, — «отказ от сотрудничества». В связи с этим мы называем ее эволюционно устойчивой стратегией для популяции, вовлеченной в данную дилемму заключенных. Обратите внимание, что при анализе этой игры с точки зрения рационального поведения «отказ от сотрудничества» — строго доминирующая стратегия. Этот результат носит общий характер: если в игре есть строго доминирующая стратегия, она обязательно будет эволюционно устойчивой.
А. Повторяющаяся дилемма заключенных
В мы говорили о том, что повторение дилеммы заключенных позволяет игрокам, осознанно придерживающимся рационального поведения, сотрудничать ради взаимной выгоды. Давайте посмотрим, есть ли подобная возможность в эволюционной игре. Предположим, каждая выбранная пара игроков разыгрывает дилемму заключенных три раза подряд. Общий выигрыш игрока от такого взаимодействия — это сумма выигрышей, полученных за три раунда.
Каждый отдельный игрок запрограммирован на использование только одной стратегии, но она должна представлять собой исчерпывающий план действий. В игре с тремя ходами стратегия может предусматривать во время второго или третьего раунда выполнение действия, которое зависит от того, что произойдет в первом или втором раунде. Например, «Я буду сотрудничать при любых обстоятельствах» и «Я буду всегда отказываться от сотрудничества при любых обстоятельствах» — это допустимые стратегии. Однако также допустима стратегия «Я начну с сотрудничества и буду продолжать его, если вы сотрудничали во время предыдущего раунда, и откажусь от него во всех последующих раундах, если вы не сотрудничали во время первого». На самом деле эта последняя стратегия — не что иное, как стратегия равноценных ответных действий, или «око за око».
Для простоты анализа в этом разделе мы будем исходить из предположения, что в популяции могут существовать только два типа стратегий: «всегда отказ от сотрудничества» (В) и «око за око» (О). Из популяции случайным образом выбираются пары игроков, после чего каждая пара проводит игру определенное количество раз. Уровень приспособленности каждого игрока представляет собой сумму его выигрышей от всех повторений игры против конкретного соперника. Мы проанализируем, что происходит в случае двух, трех и n таких повторений в каждой паре.
I.-Игра с двумя повторениями. На рис. 12.2 представлена таблица выигрышей для игры, в которой встречаются два представителя популяции рестораторов и играют друг против друга в точности два раза. Если оба игрока относятся к типу В, оба откажутся от сотрудничества в обоих случаях, тогда, как показано на , каждый из них получит выигрыш 288 в каждом раунде игры, то есть в сумме 576. Если оба игрока относятся к типу О, отказа не будет и каждый игрок получит в каждом раунде выигрыш 324, в сумме 648. Если один игрок относится к типу В, а другой к типу О, то во время первого раунда игрок типа В откажется сотрудничать, а игрок типа О будет сотрудничать; в итоге у первого выигрыш составит 360, а у второго — 216. Во время второго раунда оба игрока откажутся сотрудничать и получат выигрыш по 288 каждый. Таким образом, общий выигрыш игрока типа В будет 360 + 288 = 648, а игрока О — 216 + 288 = 504.
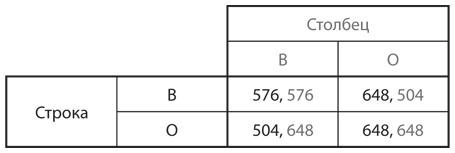
Рис. 12.2. Исходы дилеммы заключенных с двумя повторениями (в сотнях долларов в месяц)
В дважды повторяющейся дилемме заключенных мы видим, что стратегия В («всегда отказ от сотрудничества») — слабо доминирующая. Очевидно, что, если популяция состоит только из игроков типа В, мутанты О-типа не смогут ее захватить, поэтому В — эволюционно устойчивая стратегия. Но если популяция включает исключительно игроков типа О, мутанты В-типа не могут добиться большего, чем игроки О-типа. Означает ли это, что стратегия О («око за око») должна быть еще одной эволюционно устойчивой стратегией, подобно тому как в случае анализа этой игры с точки зрения рационального поведения игроков был бы сделан вывод о существовании равновесия Нэша? Ответ: нет. Если популяция изначально состоит только из игроков типа О и в игру вступают немногочисленные мутанты типа В, то последние в основном будут встречаться с игроками преобладающего типа О и получат такие же выигрыши, как и выигрыш игрока типа О в паре с другим игроком типа О. Но иногда мутант типа В будет встречаться с другим мутантом типа В и тогда получит более высокий выигрыш, чем получил бы игрок типа О в паре с игроком типа В. Таким образом, у мутантов немного более высокий уровень приспособленности, чем у представителей преобладающего фенотипа, и это преимущество приводит к увеличению (хотя и медленному) их доли в популяции. Следовательно, мутанты типа В все же могут успешно захватить популяцию, состоящую только из игроков типа О, а значит, эту стратегию нельзя назвать эволюционно устойчивой.
Наши рассуждения основаны на двух критериях определения эволюционно устойчивой стратегии. Во-первых, мы анализируем, получает ли мутант более высокий или низкий результат, чем преобладающий фенотип, когда каждый противостоит игроку преобладающего типа. Если этот первичный критерий дает четкий ответ, значит вопрос решен. Но если первичный критерий дает равный счет, мы используем вторичный критерий, позволяющий определить победителя: добивается ли мутант большего или меньшего, чем преобладающий фенотип, когда каждый противостоит мутанту? Равный счет бывает крайне редко, поэтому обычно необходимости применять вторичный критерий нет, но он есть в резерве для таких ситуаций, как отображенная на .
II.-Игра с тремя повторениями. Теперь предположим, что каждая подобранная пара игроков из популяции (В, О) играет в эту игру три раза. На рис. 12.3 представлены итоговые показатели приспособленности по всем трем раундам для каждого типа игроков в паре с соперниками каждого типа.
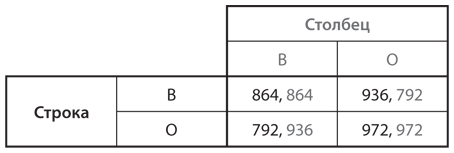
Рис. 12.3. Исходы дилеммы заключенных с тремя повторениями (в сотнях долларов в месяц)
Для того чтобы увидеть, как повышаются показатели приспособленности, рассмотрим пару примеров. Когда встречаются два игрока типа О, оба идут на сотрудничество в первом раунде, а значит, оба его продолжат и во втором, и в третьем раундах. При этом игроки каждый раз получают по 324, что в сумме дает каждому из них выигрыш 972 за три месяца. Когда игрок типа О встречается с игроком типа В, второй получает хороший результат в первом раунде (360 в паре с игроком В и 216 в паре с игроком О), но во втором и третьем раундах игрок типа О также отказывается от сотрудничества и каждый из них получает по 288 в обоих раундах (в сумме выигрыш игрока типа В равен 936, а типа О — 792).
Относительная приспособленность двух типов зависит от состава популяции. Если она почти полностью состоит из игроков типа В, то у типа В более высокий уровень приспособленности, чем у типа О (поскольку при встрече игроков типа В в основном с другими игроками типа В они в большинстве случаев получают выигрыш 864, а игроки типа О — 792). С другой стороны, если в популяции преобладают игроки типа О, у типа О более высокий уровень приспособленности, чем у типа В (так как игроки типа О получают выигрыш 972 при встрече в основном с другими представителями типа О, а выигрыш игроков типа В в такой ситуации составляет 936). Уровень приспособленности каждого типа выше, если он уже преобладает в популяции. Следовательно, тип О не может успешно захватить популяцию, состоящую из игроков типа В, и наоборот. Таким образом, существуют две возможные эволюционно устойчивые конфигурации популяции: в одной эволюционно устойчивая стратегия — стратегия В («всегда отказ от сотрудничества»), а в другой — стратегия О («око за око»).
Теперь рассмотрим эволюционную динамику в случае, когда исходная популяция представляет собой комбинацию двух типов. Как распределится ее состав с течением времени? Допустим, доля x в популяции — это игроки типа О, а остальная часть (1 – x) — игроки типа В. Отдельный игрок типа В, выставленный против различных соперников, выбранных из данной популяции, получает выигрыш 936 в противостоянии с игроком типа О, что происходит в x случаях, и выигрыш 864 в противостоянии с другим игроком типа В, что наблюдается в (1 – x) случаях. Это дает следующий ожидаемый выигрыш каждого игрока типа В:
936x + 864(1 – x) = 864 + 72x.
Аналогичным образом отдельный игрок типа О получает такой ожидаемый выигрыш:
972x + 792(1 – x) = 792 + 180x.
Стало быть, уровень приспособленности игрока типа О выше уровня приспособленности игрока типа В, если первый в среднем получает больше, то есть при выполнении следующего условия:
792 + 180x > 864 + 72x,
108x > 72,
x > 2/3.
Иными словами, если более двух третей (67%) популяции уже принадлежат к типу О, то у игроков этого типа более высокий уровень приспособленности и их доля будет расти, пока не достигнет 100%. Если в начале игры в популяции менее 67% игроков типа О, тогда у игроков типа В более высокий уровень приспособленности и доля игроков типа О будет падать, пока не достигнет 0%, то есть популяция будет полностью состоять из игроков типа В. Эволюционная динамика смещает популяцию к одному из двух крайних состояний, каждое из которых может быть эволюционно устойчивой стратегией. Эта динамика приводит к тому же выводу, что и статический критерий захвата популяции мутантами. Это общее, хотя и не универсальное свойство эволюционных игр.
Таким образом, мы определили две эволюционно устойчивые конфигурации популяции. В каждой из них популяция состоит из игроков только одного типа (то есть мономорфна). Например, если изначально популяция включает 100% игроков типа О, то даже после появления небольшого количества мутантов В-типа она по-прежнему будет состоять из более чем 66,66…% игроков типа О. Другими словами, тип О останется более приспособленным, а мутирующая линия типа В исчезнет. Точно так же, если изначально популяция на 100% состоит из игроков типа В, то небольшое количество мутантов типа О (менее 66,66…%) покинет ее, а значит, уровень приспособленности игроков типа В будет выше и мутирующая линия типа О исчезнет. Как мы уже видели ранее, экспериментирующие мутанты типа N не добьются успеха в популяции типов В и О, в основном состоящей из игроков либо В-, либо О-типа.
Но что если в исходную популяцию входит ровно 66,66…% игроков типа О (и 33,33…% игроков типа В)? Тогда у обоих типов одинаковый уровень приспособленности, и мы могли бы назвать эту ситуацию полиморфизмом. Тем не менее на самом деле такая популяция неподходящий кандидат на эволюционно устойчивую конфигурацию и может поддерживать этот слабо сбалансированный исход только до появления мутанта любого типа. По воле случая такой мутант рано или поздно появится, что сместит расчеты приспособленности в пользу мутантного типа, и данное преимущество будет накапливаться до тех пор, пока не будет достигнута эволюционно устойчивая стратегия со 100% игроков этого типа. Это просто пример применения вторичного критерия определения эволюционной устойчивости. Мы иногда будем в широком смысле говорить о такой конфигурации как о неустойчивом равновесии, для того чтобы сохранить параллель с обычной теорией игр, в которой мутации не учитываются и слабо сбалансированное равновесие может существовать. Однако в рамках строгой логики биологического процесса это вообще не равновесие.
Наши рассуждения можно представить в виде простого графика, очень напоминающего те, которые мы строили при вычислении соотношений в равновесии в смешанных стратегиях с участием игроков, осознанно придерживающихся рационального поведения. Единственное различие — в эволюционном контексте соотношение стратегий, используемых игроками, не вопрос выбора, сделанного любым отдельно взятым игроком, а свойство всей популяции, как показано на рис. 12.4. На горизонтальной оси отображена доля в популяции x (от 0 до 1) игроков типа О. Уровень приспособленности показан на вертикальной оси. Каждая линия отображает уровень приспособленности одного типа. Линия, соответствующая типу О, начинается ниже (в точке 792 по сравнению с 864 в случае линии типа В) и заканчивается выше (972 против 936). Линии пересекаются при x = 0,66… . Направо от этой точки уровень приспособленности типа О выше, поэтому процент игроков данного типа в популяции с течением времени возрастает, а значение x приближается к 1. Точно так же слева от этой точки уровень приспособленности типа В выше, поэтому процент игроков В-типа в популяции с течением времени увеличивается, а значение x приближается к 0. Такие диаграммы — полезный способ наглядного представления данных, поэтому мы будем их широко использовать.
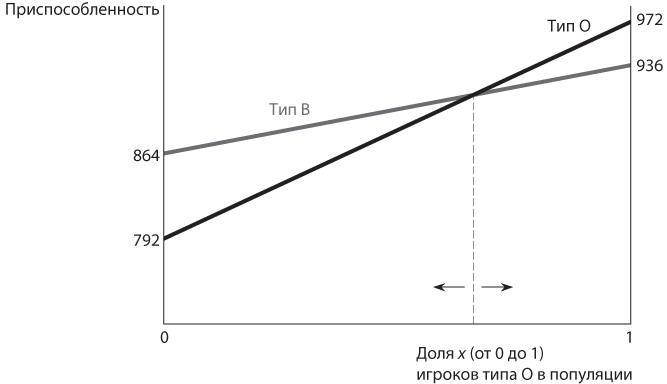
Рис. 12.4. Графики уровня приспособленности, а также равновесия в дилемме заключенных с тремя повторениями
Б. Многократно повторяющиеся игры
А что если каждая пара игроков разыграет неоговоренное количество раундов? Давайте сосредоточимся на популяции, состоящей только из игроков типа В и О, в которой взаимодействие между случайно отобранными парами происходит n раз (где n > 2). Таблица общих результатов такой игры представлена на рис. 12.5. Два игрока типа В при встрече всегда отказываются от сотрудничества и всякий раз получают выигрыш 288; иными словами, выигрыш каждого игрока составляет 288n в n раундах игры. Два игрока типа О при встрече начинают с сотрудничества, причем никто из них не отказывается от него первым, а значит, они каждый раз получают выигрыш 324, что в сумме равно 324n. Когда игрок типа В встречается с игроком типа О, в первом раунде игры игрок типа О сотрудничает, а игрок типа В отказывается от сотрудничества и в итоге получает выигрыш 360, а игрок типа О — выигрыш 216. Во всех последующих раундах игрок типа О отвечает отказом на предшествующий отказ игрока В; при этом каждый из них получает выигрыш 288 в оставшихся (n – 1) раундах. Таким образом, тип В в сумме имеет 360 + 288(n – 1) = 288n + 72 в n раундах игры против типа О, тогда как тип О — 216 + 288(n – 1) = 288n – 72 в n раундах игры против типа В.

Рис. 12.5. Исходы дилеммы заключенных с n повторениями
Если доля игроков типа О в популяции равна x, то каждый игрок типа В получает в среднем x(288n + 72) + (1 – x)288n, а типа О — x(324n) + (1 – x)(288n – 72). Следовательно, уровень приспособленности типа О выше, если
x(324n) + (1 – x)(288n – 72) > x(288n + 72) + (1 – x) 288n, 36xn > 72,
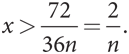
Опять же, мы снова получили две мономорфные эволюционно устойчивые стратегии: одна — когда популяция состоит только из игроков типа О (или x = 1 — к этому значению сходится процесс начиная с любого значения x > 2/n), а другая — когда популяция состоит только из игроков типа В (или x = 0 — к этому значению сходится процесс начиная с любого значения x < 2/n). Как показано на , существует только одно неустойчивое полиморфное равновесие в равновесной точке x = 2/n.
Обратите внимание, что доля игроков типа О в равновесной точке зависит от n: она меньше, когда значение n больше. При n = 10 доля игроков типа О составляет 2/10, или 0,2. Так что, если популяция изначально состоит из 20% игроков типа О, в ситуации, когда каждая пара проводит 10 повторений игры, доля игроков типа О будет расти до тех пор, пока не достигнет 100%. Вспомним, что, когда пары проводили три раунда игры (n = 3), игрокам типа О понадобилась более крупная исходная доля в размере не менее 67%, чтобы достичь аналогичного результата, а в случае всего двух повторений доля игроков типа О в популяции должна была составлять 100%, чтобы они выжили. (Мы видим причину такого исхода в нашем выражении для вычисления критического значения x, которое показывает, что при n = 2 значение x должно превышать 1, прежде чем уровень приспособленности типа О повысится.) Не забывайте также о том, что популяция, состоящая исключительно из игроков типа О, добивается сотрудничества. Таким образом, оно формируется при выполнении более широкого диапазона исходных условий, когда игра повторяется большее число раз. В этом смысле при большем количестве повторений вероятность сотрудничества увеличивается. То есть ценность установления сотрудничества повышается по мере увеличения длительности периода взаимодействия.
В. Сравнение эволюционной модели и модели рационального игрока
И наконец, вернемся к трижды повторяющейся игре, представленной на , и вместо использования эволюционной модели проанализируем ее как игру с участием двух игроков, осознанно придерживающихся рационального поведения. Каковы в ней равновесия Нэша? Есть два равновесия в чистых стратегиях, одно — когда оба игрока выбирают стратегию В, а другое — когда оба игрока выбирают стратегию О. Существует также равновесие в смешанных стратегиях, в котором стратегия О используется в 67% случаев, а стратегия В — в 33% случаев. Два первых равновесия и есть те мономорфные эволюционно устойчивые стратегии, которые мы нашли, а третье равновесие — это неустойчивое полиморфное эволюционное равновесие. Другими словами, существует тесная связь между эволюционным подходом к таким играм и подходом, основанным на концепции осознанной рациональности игроков.
Это не совпадение. Эволюционно устойчивая стратегия должна быть равновесием Нэша в игре, которую ведут осознанно рациональные игроки, с такой же структурой выигрышей. Для того чтобы в этом удостовериться, предположим на мгновение обратное. Если применение всеми игроками какой-то стратегии (назовем ее S) не приводит к равновесию Нэша, то другая стратегия (назовем ее R) должна обеспечивать более высокий выигрыш одному игроку в игре против стратегии S. Мутант, использующий стратегию R, достигнет более высокого уровня приспособленности в популяции, выбравшей стратегию S, и ему удастся захватить эту популяцию. Следовательно, стратегия S не может быть эволюционно устойчивой. Это равносильно утверждению, что если стратегия S эволюционно устойчива, то она должна быть равновесием Нэша для всех игроков, ее использующих.
Таким образом, эволюционный подход обеспечивает косвенное обоснование рационального подхода. Даже когда игроки не предпринимают осознанных действий, направленных на максимизацию своего выигрыша, если более эффективные стратегии разыгрываются чаще, а менее эффективные исчезают и в итоге процесс сводится к устойчивой стратегии, то исход должен быть таким же, как и исход в случае рациональной игры.
Хотя эволюционно устойчивая стратегия должна быть равновесием Нэша в соответствующей рациональной игре, обратное неверно. Мы привели два примера, подтверждающих этот вывод. В дважды повторяющейся дилемме заключенных на , основанной на рациональном поведении игроков, стратегия О была бы равновесием Нэша в том слабом смысле, что при выборе ее обоими игроками ни один из них не получит положительной выгоды от перехода к стратегии В. Однако в случае эволюционного подхода стратегия В может возникнуть в качестве мутации и успешно захватить популяцию типа О. А в трижды повторяющейся дилемме заключенных (см. и ) рациональная игра приведет к формированию равновесия в смешанных стратегиях. Однако его биологический аналог, полиморфное состояние, могут захватить мутанты, а значит, это равновесие не будет истинным эволюционно устойчивым. Следовательно, биологическая концепция устойчивости может помочь нам при выборе из всего множества равновесий Нэша в рациональной игре.
В нашем анализе повторяющейся игры есть одно ограничение. Изначально мы исходили из допущения о наличии всего двух стратегий, В («всегда отказ от сотрудничества») и О («око за око»). То есть предполагалось, что больше никаких стратегий нет или не может возникнуть вследствие мутации. В биологии типы появляющихся мутаций зависят от генетических факторов. В социальных, политических или экономических играх формирование новых стратегий предположительно определяется историей, культурой и опытом игроков. Кроме того, способность людей усваивать и обрабатывать информацию также должна сыграть свою роль. Тем не менее в нашей модели в данной ситуации ограничения, которые мы накладываем на комбинацию стратегий, возможных в определенной игре, имеют важные последствия в свете того, какие из этих стратегий (если они есть) могут быть эволюционно устойчивыми. Если бы мы допустили в примере с трижды повторяющейся дилеммой заключенных существование стратегии S, которая сводится к сотрудничеству во время первого раунда и отказу от него в ходе второго и третьего, то мутанты типа S могли бы успешно захватить популяцию, состоящую только из игроков типа О, поэтому стратегия О не была бы эволюционно устойчивой. Дальнейший анализ подобной перспективы содержится в примерах в конце данной главы.
3. Игра в труса
Помните юношей 1950-х годов, которые мчатся навстречу друг другу в автомобилях и ждут, кто свернет первым, чтобы избежать столкновения? Теперь предположим, что у них нет выбора: каждый генетически запрограммирован быть либо «тюфяком» (всегда сворачивать в сторону), либо «мачо» (всегда ехать прямо). Популяция состоит из комбинации двух типов. Каждую неделю случайным образом выбираются пары для участия в игре. На рис. 12.6 представлена таблица выигрышей каждого из двух игроков — скажем, А и Б. (Значения в таблице те же, что и в таблице на .)
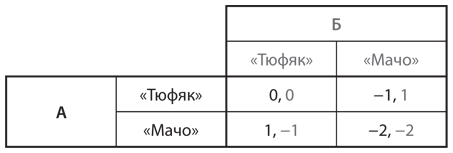
Рис. 12.6. Таблица выигрышей для игры в труса
Какие результаты получат два типа игроков? Ответ зависит от исходного соотношения типов в популяции. Если она почти полностью состоит из «тюфяков», то мутант типа «мачо» будет выигрывать и в основном получать выигрыш 1, тогда как все «тюфяки» в противостоянии с себе подобными получат большей частью нули. Но если популяция почти полностью состоит из «мачо», то мутант типа «тюфяк» получит −1, что хоть и выглядит плохо, но все же лучше выигрыша −2, который получат все «мачо». Можно представить эту ситуацию с точки зрения биологического контекста и сексизма 1950-х годов: в популяции «тюфяков» новичок «мачо» покажет всем, что они трусы, и тем самым произведет впечатление на девушек. Но если в популяции преимущественно «мачо», то в большинстве случаев они окажутся в больнице, а девушкам придется искать немногочисленных здоровых «тюфяков».
Иными словами, уровень приспособленности каждого типа выше, когда он встречается в популяции относительно редко. Следовательно, каждый тип может успешно захватить популяцию, состоящую из представителей другого типа. В таком случае следует ожидать, что оба типа в популяции находятся в равновесии; то есть эволюционно устойчивая стратегия должна представлять собой комбинацию типов, или быть полиморфной.
Для того чтобы определить соотношение «тюфяков» и «мачо» в такой эволюционно устойчивой стратегии, вычислим уровень приспособленности каждого типа в общей смешанной популяции. Пусть x — это доля «мачо», а (1 – x) — доля «тюфяков». Один «тюфяк» встречается с другим «тюфяком» и получает 0 в (1 – x) случаях, а при встрече с «мачо» — −1 в x случаев. Следовательно, уровень приспособленности «тюфяка» составляет 0 × (1 – x) – 1 × x = –x. Точно так же уровень приспособленности «мачо» равен 1 × (1 – x) – 2x = 1 – 3x. Уровень приспособленности типа «мачо» выше при выполнении условия
1 – 3x > –x,
2x < 1,
x < 1/2.
Если в популяции меньше половины «мачо», то этот тип будет более приспособленным, а его доля в популяции увеличится. Напротив, если в популяции больше половины «мачо», тогда тип «тюфяк» будет более приспособленным, а доля «мачо» будет сокращаться. В любом случае доля «мачо» в популяции будет приближаться к 1/2, и эта комбинация 50 на 50 будет эволюционно устойчивой полиморфной стратегией.
На рис. 12.7 данный исход представлен в графическом виде. Каждая прямая линия отображает приспособленность (ожидаемый выигрыш в противостоянии со случайно выбранным членом популяции) одного типа, в зависимости от доли «мачо» x. Для типа «тюфяк» эта функциональная зависимость, отображающая приспособленность этого типа как функцию доли «мачо», составляет –x, как мы определили выше. Это прямая с небольшим уклоном, которая начинается на высоте 0 при x = 0 и снижается до −1 при x = 1. Типу «мачо» соответствует функция 1 – 3x. Это линия с большим уклоном, которая начинается на высоте 1 при x = 0 и снижается до −2 при x = 1. Линия типа «мачо» проходит над линией типа «тюфяк» при x < 1/2 и под этой линией при x > 1/2. Это говорит о том, что уровень приспособленности типа «мачо» выше при малых значениях x, а уровень приспособленности типа «тюфяк» выше при больших значениях x.
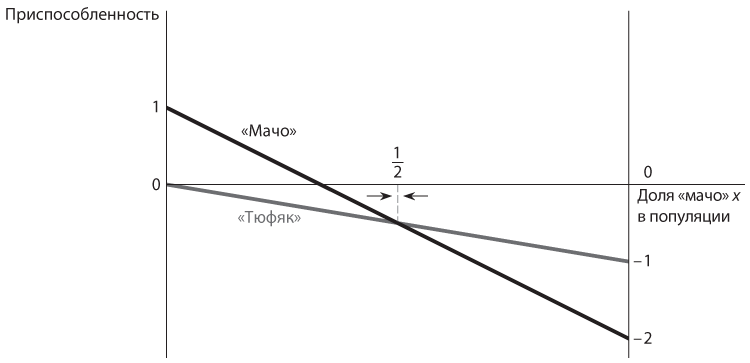
Рис. 12.7. Графики уровня приспособленности, а также полиморфное равновесие в игре в труса
Теперь можем сравнить эволюционную теорию этой игры с нашей предыдущей теорией, сформулированной в и , которая основывалась на предположении, что игроки умеют правильно рассчитывать свои лучшие стратегии. Там мы нашли три возможных равновесия Нэша: два в чистых стратегиях, когда один игрок едет прямо, а другой сворачивает, и одно в смешанных стратегиях, когда каждый игрок едет прямо с вероятностью 1/2 и сворачивает с вероятностью 1/2.
Если популяция действительно состоит из 100% игроков типа «мачо», то все они в равной степени готовы к столкновению (или в равной степени не готовы). Точно так же в популяции, включающей исключительно «тюфяков», все они в равной степени готовы отступить. Но эти мономорфные конфигурации неустойчивы. В популяции, все члены которой «мачо», мутант типа «тюфяк» получит более высокий результат и захватит ее. Наш анализ показывает, что как только в популяции появятся несколько «тюфяков», их доля неуклонно будет увеличиваться до 1/2, как бы мало их изначально ни было. Точно так же популяция, состоящая только из «тюфяков», уязвима для успешного вторжения мутантов «мачо», и этот процесс снова приводит к тому же полиморфизму. Таким образом, полиморфная конфигурация — единственный эволюционно устойчивый исход.
Наибольший интерес представляет связь между равновесием в смешанных стратегиях в рациональной игре и полиморфным равновесием в эволюционной игре. Соотношение стратегий в равновесной стратегии в первой игре точно такое же, как и соотношение типов в популяции во второй игре, где существует комбинация игроков типа «мачо» и «тюфяк» в пропорции 50 на 50. Но интерпретации у этих ситуаций разнятся: в рациональной игре каждый игрок смешивает собственные стратегии, а в эволюционной каждый член популяции использует чистую стратегию, но поскольку разные игроки применяют разные стратегии, образуется комбинация стратегий в популяции.
Такое соответствие между равновесием Нэша в рациональной игре и устойчивыми исходами игры с аналогичной структурой выигрышей в игре по эволюционным правилам — общая норма; мы увидим ее общий характер ниже в . В действительности эволюционная устойчивость обеспечивает дополнительное обоснование для выбора одного из множества равновесий Нэша в играх, основанных на концепции рационального поведения игроков.
При анализе игры в труса с рациональной точки зрения равновесие в смешанных стратегиях казалось несколько озадачивающим. Оно оставляло лазейку для ошибок, которые могли обойтись очень дорого. Каждый игрок ехал прямо в одном случае из двух, а значит, в одном случае из четырех автомобили сталкивались. Равновесие в чистых стратегиях позволяло избежать таких столкновений. В то время это могло навести вас на мысль, что в равновесии в смешанных стратегиях есть нечто нежелательное; может, вы даже задавались вопросом, зачем вообще мы тратим на него время. Теперь вы понимаете причину. На первый взгляд странное равновесие возникает как устойчивый результат естественного динамического процесса, в ходе которого каждый игрок пытается улучшить свой выигрыш в популяции, которой он противостоит.
4. Игра в доверие
Из всех широких классов стратегических игр, представленных в , мы с эволюционной точки зрения рассмотрели дилемму заключенных и игру в труса. Осталась только игра в доверие. В мы проиллюстрировали этот тип игры на примере двух студентов, Гарри и Салли, которые решают, где встретиться, чтобы выпить кофе. В эволюционном контексте каждому игроку свойственна врожденная симпатия либо к Starbucks, либо к Local Latte, а в состав популяции входит определенное число игроков каждого типа. Мы будем исходить из того, что пары игроков, которые мы разделяем на генетические категории мужчин и женщин, каждый день выбираются случайным образом для участия в данной игре. Обозначим стратегии как S (Starbucks) и L (Local Latte). На рис. 12.8 представлена таблица выигрышей при случайном отборе пар игроков; выигрыши те же, что и в таблице на .
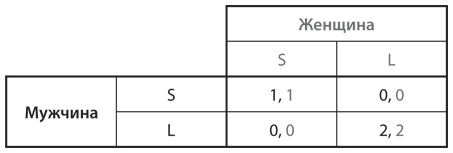
Рис. 12.8. Таблица выигрышей игры в доверие
Если бы это была игра с участием игроков, делающих рациональный выбор, в ней было бы два равновесия в чистых стратегиях: (S, S) и (L, L), причем второе лучше для обоих игроков. Если игроки общаются и координируют свои действия в явной форме, им не составит труда достичь этого равновесия. Однако если они делают выбор независимо друг от друга, им необходимо скоординировать действия посредством сходимости ожиданий, другими словами, отыскав фокальную точку.
В рациональной игре есть третье равновесие — в смешанных стратегиях, которое мы нашли в . В нем каждый игрок выбирает Starbucks с вероятностью 2/3 и Local Latte с вероятностью 1/3; ожидаемый выигрыш каждого игрока составляет 2/3. Как было показано в , этот выигрыш хуже выигрыша в случае менее привлекательного равновесия в чистых стратегиях (S, S), поскольку независимое смешивание стратегий зачастую приводит игроков к противоречивому или плохому выбору. Здесь же вероятность неблагоприятного исхода (выигрыш 0) равна 4/9: два игрока отправляются в разные места почти в половине случаев.
Что происходит в эволюционной игре? Каждый член большой популяции запрограммирован на выбор либо S, либо L. Произвольно отобранным парам таких игроков дается задание попытаться встретиться. Предположим, x — это доля в популяции игроков типа S, а (1 – x) — доля игроков типа L. Тогда уровень приспособленности определенного игрока типа S (его ожидаемый выигрыш от случайной встречи такого рода) составляет x × 1 + (1 – x) × 0 = x. Аналогично, уровень приспособленности каждого игрока типа L равен x × 0 + (1 – x) × 2 = 2(1 – x). Следовательно, уровень приспособленности типа S выше при х > 2(1 – x) или x > 2/3, а типа L — при x < 2/3. В равновесной точке x = 2/3 оба типа в равной степени приспособлены.
Как и в игре в труса, те же значения вероятности, которые относятся к равновесию в смешанных стратегиях, полученному в результате рационального выбора, появляются и при ведении игры по эволюционным правилам в виде соотношения типов в популяции при полиморфном равновесии. Однако теперь это смешанное равновесие неустойчиво. Малейшее случайное отклонение доли х от равновесной точки 2/3 запустит кумулятивный процесс, который сместит комбинацию типов в популяции далеко от равновесной точки. Если значение x превысит 2/3, уровень приспособленности игроков типа S повысится и он станет еще быстрее расти количественно, еще больше увеличивая значение x. Если значение x окажется меньше 2/3, уровень приспособленности игроков типа L повысится и он станет еще быстрее расти количественно, еще больше снижая значение x. В итоге значение x либо повысится до 1, либо упадет до 0, в зависимости от вида отклонения. Особенность ситуации состоит в том, что в игре в труса каждый тип был более приспособленным при меньшей доле в популяции, поэтому соотношение типов в ней стремилось от экстремальных значений в равновесной точке, попадающей в средний диапазон. Напротив, в игре в доверие уровень приспособленности каждого типа выше при большем количестве членов соответствующего типа в популяции; риск не встретиться с другим игроком снижается по мере увеличения доли игроков того же типа, поэтому соотношение типов в популяции стремится к экстремальным значениям.
На рис. 12.9, очень похожем на , представлены графики уровня приспособленности и равновесия в игре в доверие. Две линии отображают приспособленность двух типов в зависимости от их соотношения в популяции. Пересечение линий образует равновесную точку. Единственное отличие — при удалении от равновесной точки более многочисленный тип становится более приспособленным, тогда как на это был менее многочисленный тип.
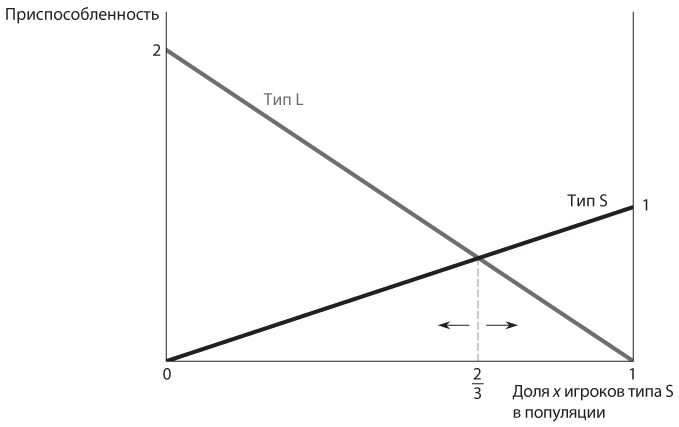
Рис. 12.9. Графики уровня приспособленности, а также равновесия в игре в доверие
Поскольку каждый тип менее приспособлен при небольшой численности, только две крайние мономорфные конфигурации популяции могут находиться в эволюционно устойчивом состоянии. Легко убедиться, что оба исхода — это эволюционно устойчивые стратегии согласно статическому критерию: захват другого типа небольшой популяцией мутантов сойдет на нет, потому что у немногочисленных мутантов более низкий уровень приспособленности. Таким образом, в играх в доверие, или координационных играх, в отличие от игры в труса, эволюционный процесс не сохраняет неблагоприятное равновесие, при котором существует положительная вероятность выбора игроками конфликтующих стратегий. Тем не менее эта динамика не гарантирует сходимости к более благоприятному из двух равновесий, если игра начинается с произвольной исходной комбинации фенотипов, — к чему придет популяция, зависит от того, с чего она начнет.
5. Три фенотипа в популяции
При существовании только двух возможных фенотипов (стратегий) мы можем выполнить проверку на наличие эволюционно устойчивой стратегии путем их сравнения с мутантом одного типа. Динамику популяции в эволюционной игре можно проиллюстрировать с помощью графиков, аналогичных представленным на , и . Мы покажем, как эти идеи и метод могут быть использованы, когда есть три (или более) возможных фенотипа, а также посмотрим, какие новые особенности при этом возникают.
А. Проверка стратегий на эволюционную устойчивость
Давайте еще раз проанализируем трижды повторяющуюся дилемму заключенных из и посредством включения третьего возможного фенотипа. Эта стратегия, обозначенная как Н, означает «никогда не отказываться от сотрудничества». На рис. 12.10 приведена таблица приспособленности с тремя стратегиями: В («всегда отказ от сотрудничества»), О («око за око») и Н («никогда не отказываться от сотрудничества»).
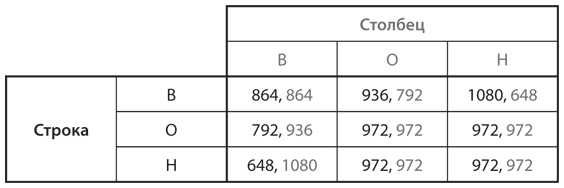
Рис. 12.10. Трижды повторяющаяся дилемма заключенных с тремя типами (выигрыши исчисляются в сотнях долларов)
Для того чтобы проверить, будет ли одна из этих стратегий эволюционно устойчивой, проанализируем, могут ли популяцию, состоящую из игроков только одного типа, захватить мутанты одного из двух других типов. Например, популяцию из игроков типа В не могут захватить мутанты типа Н или О, а значит, тип В — это эволюционно устойчивая стратегия. Но популяцию из игроков типа Н мутанты типа В захватить могут; при этом тип Н позволяет одурачить себя трижды (какой позор!). Следовательно, Н не может быть эволюционно устойчивой стратегией.
А как насчет типа О? Популяция только из игроков типа О не может быть захвачена типом В. Однако в противостоянии с мутантами типа Н тип О может оказаться на равных: обратите внимание, что в четырех ячейках таблицы у типов О и Н одинаковые выигрыши. В такой ситуации мутанты типа Н не будут размножаться, но и не вымрут. Небольшая доля мутантов может сосуществовать с популяцией, почти полностью состоящей из игроков типа О. Таким образом, тип О не удовлетворяет ни одному из критериев эволюционно устойчивых стратегий, но демонстрирует некоторую способность сопротивляться захвату.
Мы учитываем способность к адаптации, демонстрируемую типом О в нашем примере, и вводим концепцию нейтральной эволюционно устойчивой стратегии. В отличие от стандартной эволюционно устойчивой стратегии, в которой член основной популяции должен однозначно быть более приспособленным, чем мутант, в популяции с небольшой долей мутантов нейтральная устойчивость требует, чтобы член основной популяции имел как минимум такой же уровень приспособленности, как и мутант. Тогда доля мутантов не увеличивается, а может оставаться на исходном низком уровне. Это и есть случай, когда популяцию только из игроков типа О захватывает небольшое количество мутантов типа Н. В игре на присутствует одна стандартная эволюционно устойчивая стратегия (стратегия В) и одна нейтральная эволюционно устойчивая стратегия (стратегия О).
Далее проанализируем ситуацию, в которой популяцию из игроков типа О захватывают мутанты типа Н. Если доля мутантов достаточно мала, оба типа могут благополучно сосуществовать. Однако если количество мутантов составляет слишком большой процент в общей популяции, ее могут захватить мутанты В-типа: игроки типа В добиваются высоких результатов в противостоянии с типом Н, но плохо справляются с типом О. Для большей точности рассмотрим популяцию с долей x игроков типа Н и долей (1 – x) игроков типа О. Уровень приспособленности каждого из этих типов составляет 972. Уровень приспособленности мутанта типа В в этой популяции равен 936(1 – x) + 1080x = 144x + 936. Это больше 972, если 144x > 972 – 936 = 36, или x > 1/4. Таким образом, тип О может быть нейтральной эволюционно устойчивой стратегией, сосуществующей с небольшой долей мутантов типа Н, но только до тех пор, пока их доля меньше 25%.
Б. Динамика
Для того чтобы наглядно объяснить динамику в играх с тремя возможными фенотипами, обратимся к еще одной хорошо известной игре «камень, ножницы, бумага» (КНБ). В версии этой игры, основанной на концепции рационального поведения игрока, все участники одновременно выбирают одно из трех возможных действий: камень (сложить кулак), бумага (расправить ладонь) или ножницы (сделать движение двумя пальцами, напоминающее ножницы). Правила игры гласят, что камень побеждает («разбивает») ножницы, ножницы побеждают («режут») бумагу, бумага побеждает («обертывает») камень; при одинаковых движениях будет ничья. Если игроки выбирают разные действия, победитель получает выигрыш 1, а проигравший выигрыш −1; в случае ничьей выигрыш обоих игроков составляет 0.
В качестве примера эволюционной игры рассмотрим ситуацию, с которой сталкиваются пятнистобокие игуаны, обитающие на побережье Калифорнии. Для этого вида характерны три типа поведения самцов при спаривании, причем каждый тип поведения ассоциируется с окраской горла самца. Синегорлые самцы (стражи) охраняют небольшое количество самок и отражают попытки желтогорлых самцов (тихони) прокрасться и спариться с самкой, оставшейся без защиты. Такая стратегия желтогорлого самца эффективна против оранжевогорлых самцов (агрессоров), которые держат большие гаремы и часто преследуют других самцов, как правило, синегорлых, которых оранжевогорлые самцы могут одолеть благодаря своей агрессивности. Взаимодействие между тремя типами самцов можно смоделировать посредством структуры выигрышей игры КНБ, представленной на рис. 12.11, где показаны только выигрыши игрока, которому соответствуют строки. Мы включаем в таблицу столбец для q-комбинации, что позволит нам проанализировать эволюционный эквивалент равновесия в смешанных стратегиях в этой игре, то есть комбинацию типов в популяции.
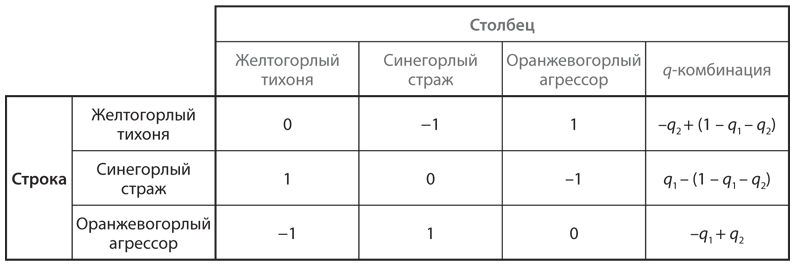
Рис. 12.11. Выигрыши в эволюционной игре с тремя фенотипами
Допустим, q1 — доля желтогорлых игуан в популяции, q2 — доля синегорлых игуан, а (1 – q1 – q2) — доля оранжевогорлых игуан. В правом столбце таблицы показаны выигрыши каждого игрока строки в противостоянии с такой комбинацией фенотипов, то есть это уровень приспособленности игроков, которым соответствуют строки. Предположим, что в популяции пятнистобоких игуан доля каждого типа увеличивается, когда его приспособленность имеет положительное значение, и уменьшается в случае отрицательного значения. Тогда q1 повышается только при выполнении условия
–q2 + (1 – q1 – q2) > 0,
q1 + 2q2 < 1.
Доля желтогорлых игуан в популяции увеличивается, когда q2 (доля синегорлых игуан) небольшая или (1 – q1 – q2) (доля оранжевогорлых игуан) большая. Это имеет смысл: желтогорлые самцы не особо успешны в противостоянии с синегорлыми, но весьма хороши в противоборстве с оранжевогорлыми самцами. Аналогичным образом q2 повышается только при выполнении условия
q1 – (1 – q1 – q2) > 0,
2q1 + q2 > 1.
Синегорлые самцы добиваются лучших результатов, когда доля желтогорлых соперников большая или оранжевогорлых малая.
Графики на рис. 12.12 наглядно демонстрируют динамику популяции и полученных в итоге равновесий в этой игре. Треугольный сегмент, ограниченный осями координат и линией q1 + q2 = 1, содержит все возможные равновесные комбинации q1 и q2. В нем есть также две прямые линии. Первая линия (более пологая) — это q1 + 2q2 = 1, равновесная линия для q1; если комбинация q1 и q2 ниже этой линии, q1 (доля желтогорлых самцов) возрастает; если комбинация q1 и q2 выше этой линии, q1 сокращается. Вторая линия (линия с большим наклоном) — это линия 2q1 + q2 = 1, равновесная линия для q2. Справа от нее (когда 2q1 + q2 > 1) q2 возрастает; слева (когда 2q1 + q2 < 1) q2 сокращается. Стрелками обозначены направления изменения соотношений типов в популяциях; серые линии соответствуют типичным динамическим путям. Общая идея та же, что и на .
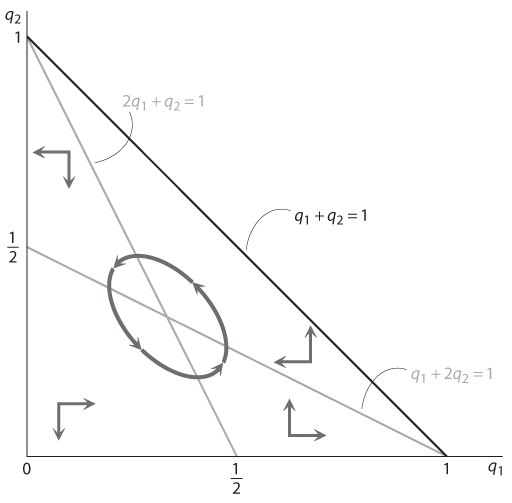
Рис. 12.12. Динамика популяции в эволюционной версии игры КНБ
На каждой из двух серых линий один из показателей q1 и q2 не возрастает и не уменьшается. Следовательно, их пересечение образует точку, в которой q1, q2, а значит, и (1 – q1 – q2) — постоянные. Это означает, что эта точка соответствует полиморфному равновесию. Несложно проверить, что в данном случае q1 = q2 = 1 – q1 – q2 = 1/3. Эти доли типов в популяции эквивалентны вероятностям стратегий в равновесии со смешанными стратегиями в рациональной версии игры КНБ.
Устойчив ли этот полиморфный исход? В общем мы не можем дать однозначного ответа. Динамика указывает на наличие путей (обозначенных на в виде эллипса), которые формируются вокруг данного исхода. Разворачиваются ли они по убывающей спирали по направлению к точке пересечения (в таком случае можно говорить об устойчивости) или по расходящейся спирали (что указывает на неустойчивость), зависит от конкретной реакции соотношения типов в популяции на изменение уровня приспособленности. Эти пути могут даже проходить по траектории, изображенной на , не приближаясь и не отдаляясь от равновесия.
Фактические данные говорят о том, что популяция пятнистобоких игуан вращается вокруг точки полиморфного равновесия с равным соотношением типов; при этом один тип на какой-то период становится более распространенным, но затем более сильный соперник берет над ним верх. Вопрос о том, приближается ли этот цикл к устойчивому равновесию, остается темой дальнейшего изучения. Как минимум один пример такого же взаимодействия, как и в случае КНБ, относится к трем штаммам кишечной палочки, вызывающей пищевые отравления. Каждый штамм бактерии вытесняет любой другой, но вытесняется третьим, как и в игре с тремя типами, о которой шла речь выше. Ученые, изучающие соперничество между тремя штаммами кишечной палочки, доказали, что полиморфное равновесие может быть устойчивым, если взаимодействие между парами остается локальным, а небольшие колонии каждого штамма постоянно перемещаются.
6. Игра «ястреб–голубь»
Игра «ястреб–голубь» стала первой изученной биологами в процессе разработки теории эволюционных игр. В ней есть полезные параллели с дилеммой заключенных и игрой в труса, поэтому мы описываем ее здесь, чтобы закрепить и углубить ваше понимание соответствующих концепций.
В игре участвуют не птицы этих двух видов, а двое животных одного и того же вида, а «ястреб» и «голубь» — просто названия их стратегий. Суть игры — соперничество за ресурс. Стратегия «ястреб» агрессивна и направлена на получение всего ресурса стоимостью V. Стратегия «голубь» компромиссна и сводится к готовности разделить ресурс и избежать драки. Когда два игрока типа «ястреб» противостоят друг другу, они вступают в драку. Каждое животное с одинаковой вероятностью (равной 1/2) может либо победить и получить V, либо проиграть, получить травмы и –C. Следовательно, ожидаемый выигрыш каждого игрока равен (V – C)/2 . Когда в игру вступают два «голубя», они без драки делят между собой ресурс, поэтому выигрыш каждого из них составляет V/2. Когда игрок типа «ястреб» вступает в противостояние с игроком типа «голубь», последний спасается бегством и получает выигрыш 0, тогда как первый — выигрыш V. На рис. 12.13 представлена таблица выигрышей в этой игре.

Рис. 12.13. Таблица выигрышей для игры «ястреб–голубь»
Анализ этой игры аналогичен анализу дилеммы заключенных и игры в труса, только в ней числовые выигрыши заменены алгебраическими символами. Мы сопоставим равновесия в этой игре, когда игроки рационально выбирают стратегию «ястреб» или «голубь», после чего сравним исходы игры, когда игроки действуют автоматически, а успех вознаграждается более быстрым воспроизводством.
А. Рациональный стратегический выбор и равновесие
- Если V > C, то это дилемма заключенных, в которой стратегия «ястреб» соответствует стратегии «отказ от сотрудничества», а стратегия «голубь» — стратегии «сотрудничать». Стратегия «ястреб» — доминирующая для каждого игрока, но комбинация стратегий «голубь»/«голубь» — более благоприятный исход для обоих игроков.
- Если V < C, тогда это игра в труса. Теперь (V – C)/2 < 0, а значит, «ястреб» больше не доминирующая стратегия. В игре два равновесия Нэша в чистых стратегиях: «ястреб»/«голубь» и «голубь»/«ястреб». В игре также есть равновесие в смешанных стратегиях, при котором вероятность p выбора игроком Б стратегии «ястреб» имеет такое значение, которое поддерживает безразличие игрока А в отношении выбора стратегий:
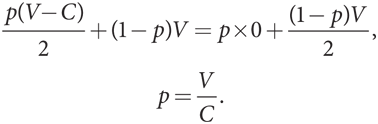
Б. Эволюционная устойчивость при V > C
Начнем с популяции, состоящей преимущественно из «ястребов», и проверим, могут ли ее захватить мутанты типа «голубь». Придерживаясь условных обозначений для подобных игр, мы могли бы выразить долю мутантного фенотипа в популяции как m (от слова «mutant»), но для ясности будем использовать для мутанта типа «голубь» обозначение d (от «dove»). Таким образом, доля «ястребов» в популяции составляет (1 – d). Тогда в противостоянии со случайно выбранным соперником «ястреб» будет встречаться с «голубем» в d случаях и получит V в каждом из них, а также встретится с другим «ястребом» в (1 – d) случаях и получит (V – C)/2 в каждом. Следовательно, уровень приспособленности «ястреба» равен [dV + (1 – d)(V – C)/2]. Аналогичным образом уровень приспособленности одного из мутантов типа «голубь» составляет [d(V/2) + (1 – d)×0]. Поскольку V > C, отсюда следует, что (V – C)/2 > 0. Кроме того, V > 0 подразумевает, что V > V/2. В таком случае при любом значении d от 0 до 1 имеем
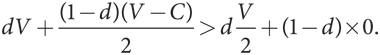
Стало быть, у «ястреба» более высокий уровень приспособленности, поэтому мутанты типа «голубь» не могут захватить популяцию. Стратегия «ястреб» эволюционно устойчива, а популяция мономорфна (все «ястребы»).
То же самое верно и для любой доли «голубей» в популяции при всех значениях d. Следовательно, какой бы ни была исходная комбинация типов, доля «ястребов» будет расти и они будут доминировать. Кроме того, если исходная популяция состоит только из «голубей», мутанты типа «ястреб» могут ее захватить. Таким образом, эта динамика говорит о том, что «ястреб» — единственная эволюционно устойчивая стратегия. Данный алгебраический анализ подтверждает и обобщает сделанный ранее вывод в числовом примере дилеммы заключенных в контексте игры в ценообразование (см. ).
В. Эволюционная устойчивость при V < C
Если исходная популяция преимущественно «ястребы» с небольшой долей d мутантов типа «голубь», то у каждого из них такая же функция уровня приспособленности, как и функции, выведенные в . Однако когда V < C, (V – C)/2 < 0. Мы по-прежнему имеем V > 0, а значит, V > V/2. Но поскольку значение d очень маленькое, сравнение этих членов с (1 – d) играет гораздо более важную роль, чем сравнение с d, поэтому
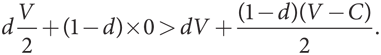
Следовательно, уровень приспособленности мутантов типа «голубь» выше уровня приспособленности доминирующего типа «ястреб», поэтому мутанты типа «голубь» могут захватить популяцию.
Однако если исходная популяция почти полностью состоит из «голубей», мы должны проанализировать, может ли небольшая доля h мутантов типа «ястреб» захватить ее. (Обратите внимание, что, поскольку мутант теперь относится к типу «ястреб», мы использовали символ h (hawk) для обозначения доли мутантов-захватчиков.) Уровень приспособленности мутантов типа «ястреб» [h(V – C)/2 + (1 – h)V] сопоставим c [h × 0 + (1 – h)(V/2)] в случае мутантов типа «голубь». И снова V < C подразумевает, что (V – C)/2 < 0, а V > 0 подразумевает, что V > V/2. Но когда значение h небольшое, получаем
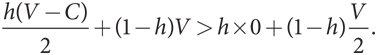
Это неравенство показывает, что уровень приспособленности «ястребов» выше, поэтому они захватят популяцию «голубей». Таким образом, мутанты каждого типа могут захватить популяцию другого типа. Поэтому она не может быть мономорфной и ни один чистый фенотип не может быть эволюционно устойчивой стратегией. Алгебраические расчеты снова подтверждают сделанный ранее вывод в числовом примере дилеммы заключенных в контексте игры в труса (см. и ).
А что происходит в популяции, когда V < C? Существуют два сценария. В первом каждый игрок придерживается чистой стратегии, но в популяции наблюдается устойчивая комбинация игроков, использующих разные стратегии. Это полиморфное равновесие, сформировавшееся в игре в труса, о которой шла речь в . Второй сводится к применению каждым игроком смешанной стратегии. Мы начнем с полиморфного случая.
Г. V < C: устойчивая полиморфная популяция
Когда доля «ястребов» в популяции равна h, уровень их приспособленности составляет h(V – C)/2 + (1 – h)V, а уровень приспособленности «голубя» — h × 0 + (1 – h)(V/2). Уровень приспособленности «ястреба» выше, если
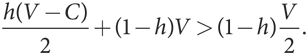
Это неравенство можно упростить:
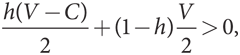
V – hC > 0,
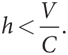
В таком случае уровень приспособленности типа «голубь» выше, когда h > V/C, или когда (1 – h) < 1 – (V/C) = (C – V)/C. Стало быть, каждый тип более приспособлен, если его численность меньше. Следовательно, мы имеем устойчивое полиморфное равновесие в равновесной точке, в которой доля «ястребов» в популяции составляет h = V/C. Это и есть рассчитанная в вероятность, с которой каждый отдельный игрок выбирает стратегию «ястреб» в равновесии Нэша в смешанных стратегиях данной игры при условии рационального поведения игроков. К тому же мы также получили эволюционное «обоснование» исхода в виде смешанной стратегии в игре в труса.
Мы предоставляем вам возможность построить для этого случая график, аналогичный представленному на . Для этого вам понадобится определить динамику, в соответствии с которой доли каждого типа в популяции сходятся к устойчивой равновесной комбинации.
Д. V < C: каждый игрок смешивает стратегии
Вспомните рассчитанную в равновесную смешанную стратегию в рациональной игре, где p = V/C — вероятность выбора стратегии «ястреб», а (1 – p) — вероятность выбора стратегии «голубь». Есть ли параллель в эволюционной версии игры, когда фенотип выбрал бы смешанную стратегию? Проанализируем такую возможность. У нас по-прежнему есть игроки типа Я, использующие чистую стратегию «ястреб», и игроки типа Г, использующие чистую стратегию «голубь». Но теперь может существовать еще и третий фенотип С, применяющий смешанную стратегию, включая в нее стратегию «ястреб» с вероятностью p = V/C и стратегию «голубь» с вероятностью 1 – p = 1 – (V/C) = (C – V)/C.
Когда Я или Г встречает С, их ожидаемый выигрыш зависит от p — вероятности того, что С выберет стратегию Я, и от (1 – p) — вероятности того, что С выберет стратегию Г. Тогда каждый игрок получает p, умноженное на его выигрыш в игре против Я, плюс (1 – p), умноженное на его выигрыш в игре против Г. Таким образом, когда Я противостоит С, его ожидаемый выигрыш составит
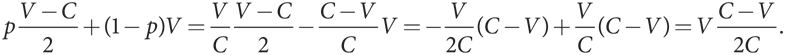
А когда Г противостоит С, его выигрыш равен
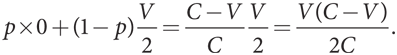
Уровни приспособленности двух типов одинаковы. Это не должно стать неожиданностью: соотношение чистых стратегий должно обеспечивать именно такое равенство. Тогда игрок типа С в противостоянии с другим игроком типа С получит тот же ожидаемый выигрыш. Для того чтобы было проще ссылаться на него в дальнейшем, обозначим его символом K, где K = V(C – V)/2C.
Но такое равенство создает проблему при проверке стратегии С на эволюционную устойчивость. Предположим, популяция целиком состоит из игроков типа С и в нее вторгаются мутанты типа Я, составляющие совсем малую долю h от общей численности популяции. Тогда типичный мутант получит ожидаемый выигрыш h(V – C)/2 + (1 – h)K. Для того чтобы вычислить ожидаемый выигрыш игрока типа С, необходимо учесть, что он противостоит другому игроку типа С в (1 – h) случаях и каждый раз получает выигрыш K. Далее он вступает в противостояние с игроком типа Я в h взаимодействиях и в их ходе использует стратегию Я в p случаях и получает выигрыш (V – C)/2 и стратегию Г в (1 – p) случаев и получает выигрыш 0. Таким образом, общий ожидаемый выигрыш (уровень приспособленности) игрока типа С составляет
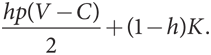
Поскольку у h очень малое значение, приспособленность игроков типа С и мутантов типа Я почти эквивалентна. Дело в том, что, когда мутантов очень мало, игроки как типа Я, так и типа С в основном противостоят только игрокам типа С и, как мы только что выяснили, в этом взаимодействии у обоих типов одинаковый уровень приспособленности.
Эволюционная устойчивость зависит от того, будет ли исходная популяция типа С более приспособленной, чем мутант типа Я, когда каждый из них противостоит одному из немногочисленных мутантов. В алгебраической форме тип С более приспособлен, чем тип Я, в противоборстве с другими мутантами типа Я, когда pV(C – V)/2C = pK > (V – C)/2. В нашем примере это условие выполняется, так как V < C, то есть (V – C) имеет отрицательное значение, а K имеет положительное значение. На интуитивном уровне это условие говорит нам о том, что мутант типа Я всегда будет получать более низкие результаты в противостоянии с другим мутантом типа Я из-за высоких издержек в связи с дракой, но тип С вступает в драку только иногда, а значит, несет такие издержки лишь в p случаях. В целом тип С добивается большего в противостоянии с мутантами.
Аналогично успех вторжения типа Г в популяцию С зависит от сравнения уровня приспособленности мутанта типа Г с уровнем приспособленности мутанта типа С. Как и раньше, мутант противостоит другому игроку типа Г в d случаях, а игроку типа С в (1 – d) случаях. Тип С также противостоит другому игроку типа С в (1 – d) случаях, однако в d случаях С противостоит Г и использует стратегию Я в p из этих случаев, получая при этом выигрыш pV, а также применяет стратегию Г в (1 – p) случаях, получая при этом выигрыш (1 – p)V/2. Из этого следует, что уровень приспособленности типа «голубь» составляет [dV/2 + (1 – d)K], тогда как уровень приспособленности типа С равен d × [pV+(1 – p)V/2] + (1 – d)K. Последние члены выражений, описывающих уровни приспособленности, идентичны, а значит, вторжение «голубей» может быть успешным, только если V/2 больше pV + (1 – p)V/2. Это условие не выполняется: последнее выражение содержит взвешенное среднее V и V/2, которое больше V/2 при V > 0. Таким образом, вторжение мутантов типа «голубь» не может завершиться успехом.
Этот анализ говорит о том, что С — эволюционно устойчивая стратегия. Следовательно, если V < C, популяция может продемонстрировать любой из двух эволюционно устойчивых исходов. Один подразумевает смешение типов (устойчивый полиморфизм), а другой — присутствие в популяции только одного типа, смешивающего стратегии в том же соотношении, которое определяет полиморфизм.
Е. Немного общей теории
Теперь обобщим идеи, представленные в данном разделе, чтобы получить теоретическую основу и набор инструментов для дальнейшего использования. Такое обобщение неизбежно требует несколько более абстрактных обозначений и немного алгебры. В связи с этим мы рассмотрим только мономорфные равновесия в одном виде. Читатели, которые владеют математикой на должном уровне, смогут по аналогии описать полиморфные случаи с двумя видами. Читатели, которые не готовы к восприятию данного материала или для них он не представляет интереса, могут пропустить этот раздел без ущерба для целостности изложения материала.
Проанализируем взаимодействие между случайно отобранными из одного вида парами, популяции которого доступны стратегии I, J, K, …, среди которых могут быть как чистые, так и смешанные. Каждый отдельный член популяции запрограммирован на использование только одной из этих стратегий. Обозначим E(I, J) выигрыш игрока I от одного взаимодействия с игроком J. Выигрыш игрока I в противостоянии с другим представителем своего типа составляет E(I, I) в той же системе обозначений. Пусть W(I) — уровень приспособленности игрока I. Это просто его ожидаемый выигрыш в противостоянии с произвольно выбранными соперниками, когда вероятность встретить игрока определенного типа равна доле этого типа в популяции.
Допустим, популяция состоит только из игроков типа I. Проанализируем, может ли такая конфигурация быть эволюционно устойчивой. Для этого представим, что популяцию захватывают несколько мутантов типа J; значит, доля m мутантов в популяции очень маленькая. Уровень приспособленности типа I составляет
W(I) = mE(I, J) + (1 – m) E(I, I).
Уровень приспособленности мутанта равен
W(J) = mE(J, J) + (1 – m) E(J, I).
Следовательно, разница между уровнями приспособленности основного и мутантного типов популяции определяется формулой
W(I) – W(J) = m[E(I, J) – E(J, J)] + (1 – m) [E(I, I) – E(J, I)].
Поскольку m очень маленькое, уровень приспособленности основного типа будет выше по сравнению с приспособленностью мутанта, если вторая часть представленного выражения имеет положительное значение, то есть
W(I) > W(J), если E(I, I) > E(J, I).
В таком случае основной тип в популяции не может быть захвачен; он более приспособлен, чем мутантный тип, когда каждый противостоит члену основного типа. Это и есть первичный критерий эволюционной устойчивости. Напротив, если W(I) < W(J) — тогда E(I, I) < E(J, I) — вторжение мутантов типа J будет успешным, поэтому популяция, полностью состоящая из игроков типа I, не может быть эволюционно устойчивой.
Однако возможна ситуация, когда E(I, I) = E(J, I), как и происходит на самом деле, если популяция изначально состоит из одного фенотипа, смешивающего чистые стратегии I и J (мономорфное равновесие со смешанной стратегией), как было в последнем варианте игры «ястреб–голубь» (). Тогда разность между W(I) и W(J) зависит от того, насколько успешно оба типа противостоят мутантам. Когда E(I, I) = E(J, I), получаем W(I) > W(J), если E(I, J) > E(J, J). Это вторичный критерий эволюционной устойчивости, который следует применять, только если первичный критерий не позволяет сделать однозначный вывод, то есть если E(I, I) = E(J, I).
При применении вторичного критерия — поскольку E(I, I) = E(J, I) — существует вероятность того, что он также не позволит сделать однозначный вывод. Другими словами, возможно, что E(I, J) = E(J, J). Это случай нейтральной устойчивости, о которой шла речь в . Если ни первичный, ни вторичный критерий не обеспечивают убедительных результатов, то I считается нейтральной эволюционно устойчивой стратегией.
Обратите внимание, что у первичного критерия есть одна особенность. Он гласит, что если стратегия I эволюционно устойчива, то для всех остальных стратегий J, которые может попробовать применить мутант, E(I, I) ≥ E(J, I). Это означает, что стратегия I — наилучший ответ на саму себя. Иными словами, если бы члены этой популяции вдруг начали играть как придерживающиеся рационального поведения игроки, применение ими всеми стратегии I было бы равновесием Нэша. Таким образом, эволюционная устойчивость подразумевает наличие равновесия Нэша в соответствующей рациональной игре!
Это поразительный результат. Если вас не удовлетворяло предположение о рациональном поведении, лежащее в основе теории равновесий Нэша, представленной в предыдущих главах, и вы обратились к эволюционной теории в поисках более подходящего объяснения, то теперь вы убедились, что она дает те же результаты. Поистине занимательное биологическое описание (фиксированное не максимизирующее поведение, но при этом выбор в ответ на полученный в итоге уровень приспособленности) не обеспечивает новых исходов, а, скорее, предоставляет косвенное обоснование равновесия Нэша. Когда в игре есть несколько равновесий Нэша, эволюционная динамика может даже предоставить хороший аргумент для выбора одного из них.
Тем не менее ваша укрепившаяся уверенность в равновесии Нэша должна быть взвешенной. Наше определение эволюционной устойчивости скорее статично, чем динамично. Оно лишь позволяет проверить, что конфигурация популяции (мономорфная или полиморфная с надлежащим соотношением типов), которую мы тестируем на наличие равновесия, не может быть захвачена небольшой популяцией мутантов. Такая проверка не поможет определить, исчезнут ли все нежелательные типы и будет ли достигнута равновесная конфигурация в случае произвольной исходной комбинации типов в популяции. Кроме того, проверка проводится в отношении конкретных классов мутантов, которые считаются логически возможными, но если теоретик некорректно выполнит эту классификацию и в действительности может появиться тип мутантов, который он не учел, этот мутант может совершить успешное вторжение и разрушить предполагаемое равновесие. В конце анализа дилеммы заключенных с двумя повторениями, о которой шла речь в , мы предупреждали о подобной вероятности, и в упражнениях вы увидите, как такое может произойти. И наконец, в мы убедились, что эволюционная динамика может вообще не гарантировать сходимости к более благоприятному из двух равновесий.
7. Взаимодействие всех членов популяции и между разными видами
До сих пор мы фокусировались на ситуациях, в которых каждая игра проводится между двумя игроками, отобранными из популяции случайным образом. Однако нередки случаи, когда все члены популяции играют одновременно или взаимодействуют два разных вида; они требуют специального анализа, и мы представим его в данном разделе.
А. Игра по всему полю
В ходе эволюционного взаимодействия встречаются ситуации, когда все члены популяции играют одновременно, а не парами. В биологии стадо животных с определенной комбинацией различных, заданных на генетическом уровне моделей поведения может бороться за тот или иной ресурс или территорию. В экономике или бизнесе многие компании, стратегии которых продиктованы корпоративной культурой, могут конкурировать все со всеми.
Такие эволюционные игры находятся в той же зависимости с рациональными коллективными играми из , что и парные эволюционные игры, представленные в предыдущих разделах, с рациональными играми с двумя участниками, о которых шла речь в главах 4–7. Подобно тому как мы преобразовали графики ожидаемых выигрышей из этих глав в диаграммы уровней приспособленности на , и , мы можем преобразовать графики для игр с коллективным действием (см. ) в графики приспособленности в эволюционных играх.
Рассмотрим в качестве примера вид животных, все члены которого приходят на общее пастбище. В этом виде есть два фенотипа: один агрессивно борется за пищу, а другой бродит вокруг и пытается подобрать то, что удается. Если доля агрессивных особей небольшая, для них это лучше, но если их слишком много, выиграют тихони, которые смогут добыть себе больше пищи, игнорируя постоянные схватки сородичей. По сути, это коллективная игра в труса, в которой был бы точно такой же график приспособленности, как и на . Поскольку здесь не требуется никаких новых принципов или методов, мы предоставляем вам возможность самостоятельно развить эту идею.
Б. Взаимодействие между видами
Теперь рассмотрим последний тип эволюционного взаимодействия, а именно тот, который происходит между членами не одного и того же, а разных видов. Во всех предыдущих случаях у игроков из определенной популяции были одинаковые предпочтения. Например, в игре в доверие из игроки типа L от рождения отдавали предпочтение кафе Local Latte, а игроки типа S — кафе Starbucks, однако уровень приспособленности каждого типа был выше, когда встреча происходила в Local Latte. Структура игры «битва полов» (единственный класс игр, который мы еще не проанализировали) подразумевает иную схему выигрышей. Хотя участники такой игры по-прежнему заинтересованы встретиться либо в Starbucks, либо в Local Latte (если они не встретятся, выигрыш каждого составит 0), теперь каждый тип предпочитает другое кафе. Это предпочтение позволяет выделить два типа. На языке биологии их больше нельзя рассматривать как случайно выбранные из однородной популяции животных. Они, скорее, должны принадлежать к разным видам.
Для изучения таких игр с эволюционной точки зрения расширим нашу методику на случай, когда пары образуются из спонтанным образом выбранных представителей разных видов. Предположим, существует большая популяция «мужчин» и большая популяция «женщин». Из них в случайном порядке выбирается по одному игроку, которым предлагают попытаться встретиться. Все мужчины договариваются между собой о выигрышах при выборе кафе Starbucks, Local Latte и отсутствии встречи. Все женщины договариваются о том же. Но в каждой популяции есть как противники компромисса, так и его сторонники. Противник компромисса всегда будет выбирать любимое кафе своего вида. Сторонник компромисса, понимая, что члены другого вида хотят противоположного, отправится именно в это место.
Если в случайно отобранную пару попадает противник компромисса из одного вида и сторонник компромисса из другого, в итоге будет получен исход, которому отдает предпочтение противник компромисса. Если пару образуют два противника компромисса, встреча так и не состоится; как ни странно, аналогичный результат будет получен в случае двух сторонников компромисса, поскольку каждый из них отправится в любимое кафе другого. (Не забывайте, что игроки должны делать выбор независимо друг от друга и не могут договориться о месте встречи. Возможно, даже если бы у них и получилось собраться вместе заранее, они бы попали в тупиковую ситуацию: «Нет, я настаиваю на том, чтобы уступить твоим предпочтениям».)
Мы изменим таблицу выигрышей на так, как показано на рис. 12.14, — то, что раньше было вариантами выбора, теперь выступает в качестве действий, которые предопределяет тип (противник или сторонник компромисса).
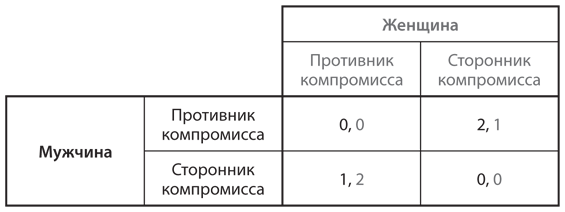
Рис. 12.14. Выигрыши в игре «битва полов»
В сравнении со всеми эволюционными играми, которые мы анализировали до этого, у данной игры есть новое свойство: игрок строки и игрок столбца — представители разных видов. Хотя каждый вид представляет собой однородную совокупность противников и сторонников компромисса, их соотношение не обязательно должно быть одинаковым в обоих видах. Следовательно, нам необходимо ввести две переменные, описывающие эти две комбинации, и изучить динамику в обоих случаях.
Пусть x — доля противников компромисса среди мужчин, а y — среди женщин. Рассмотрим конкретного противника компромисса из числа мужчин. Встречаясь с женщиной — противницей компромисса в y случаях, он получает выигрыш 0, а при встрече с женщиной — сторонницей компромисса в остальных случаях — выигрыш 2. Следовательно, его ожидаемый выигрыш (уровень приспособленности) составляет y × 0 + (1 – y) × 2 = 2(1 – y). Аналогично уровень приспособленности мужчины — сторонника компромисса равен y × 1 + (1 – y) × 0 = y. Таким образом, из всех участников игры уровень приспособленности противников компромисса выше, когда 2(1 – y) > y, или y < 2/3. Будучи более приспособленными, мужчины из числа противников компромисса будут воспроизводиться быстрее; другими словами, x увеличивается, когда y < 2/3. Обратите внимание на новый и на первый взгляд неожиданный аспект полученного исхода: уровень приспособленности каждого типа в пределах соответствующего вида зависит от доли типов в других видах. В этом нет ничего удивительного, поскольку теперь каждый вид ведет игры против другого вида.
Проанализировав аналогичным образом другой вид, получим результат, согласно которому уровень приспособленности у противников компромисса из числа женщин выше, а значит, y увеличивается при x < 2/3. Для того чтобы понять этот результат на интуитивном уровне, обратите внимание на то, что противники компромисса каждого вида добиваются более весомых результатов, когда у другого вида своих противников компромисса не особо много, поскольку при этом они достаточно часто встречались бы со сторонниками компромисса другого вида.
На рис. 12.15 показана динамика конфигураций двух видов. Переменные x и y могут принимать значения от 0 до 1, поэтому мы получили график в виде единичного квадрата с x и y на их обычных осях. Вертикальная линия AB содержит все точки, где x = 2/3 — равновесная точка, в которой значение y не увеличивается и не уменьшается. Если текущие доли типов в популяции находятся слева от этой линии (то есть x < 2/3), значение y увеличивается (смещая долю женщин — противниц компромисса в вертикальном восходящем направлении). Если текущие доли находятся справа от линии AB (x > 2/3), значение y уменьшается (движение в вертикальном нисходящем направлении). Аналогично горизонтальная линия CD отображает все точки, где y = 2/3, то есть равновесную точку для x. Когда доля женщин — противниц компромисса находится ниже этой линии (то есть когда y < 2/3), доля мужчин — противников компромисса (x) увеличивается (движение по горизонтали направо), а когда над этой линией, уменьшается, то есть при y > 2/3 (движение по горизонтали налево).
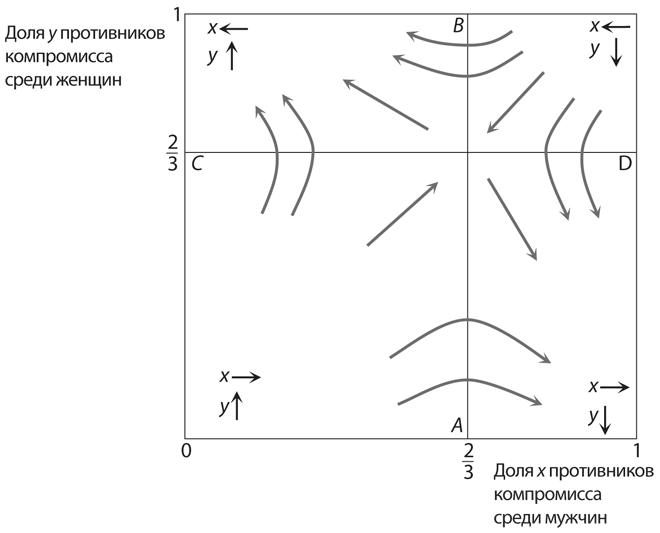
Рис. 12.15. Динамика популяций в игре «битва полов»
Объединив движение x и y, мы сможем отследить их динамические пути, чтобы определить местоположение равновесия популяции. Например, начиная с исходной точки в нижнем левом квадранте эта динамика подразумевает увеличение значений как x, так и y. Это общее перемещение (в верхний правый угол) продолжается до тех пор, пока либо x = 2/3 и y начнет уменьшаться (движение происходит в правый правый угол), либо y = 2/3 и x начнет уменьшаться (перемещение направлено в верхний левый угол). Аналогичные процессы в каждом квадранте позволяют получить криволинейные динамические пути, показанные на рис. 12.5; их подавляющее большинство ведет либо в нижний правый, либо в верхний левый угол диаграммы, то есть они сходятся в точке (1, 0) или в точке (0, 1). Таким образом, в большинстве случаев эволюционная динамика приводит к конфигурации, в которой один вид состоит только из противников компромисса, а другой — только из его сторонников. Каким будет тип того или иного вида, зависит от исходных условий. Обратите внимание, что динамический путь популяции, начиная с малого значения x и большего значения y, с большей вероятностью сперва пересечет линию CD и направится к точке (0, 1) (все члены популяции женщины — противницы компромисса, y = 1), чем сначала пересечет линию AB и направится к точке (1, 0). Те же результаты будут получены в случае исходной позиции с малым значением y и большим значением x. Вид, который начинает игру с большей долей противников компромисса, имеет преимущество в том смысле, что к ее концу будет состоять только из них и получит выигрыш 2.
Если исходные доли правильно сбалансированы, динамика популяции может привести к полиморфной точке (2/3, 2/3). Но в отличие от полиморфного исхода в игре в труса, полиморфизм в игре «битва полов» неустойчив. Большинство случайных переходов запустят кумулятивный процесс, который приведет к одному из крайних равновесий; это и есть две эволюционно устойчивые стратегии в данной игре. Это общее свойство: игры с участием разных видов могут иметь только эволюционно устойчивые стратегии, мономорфные для каждого вида.
8. Эволюция сотрудничества и альтруизма
Теория эволюционных игр основана на двух фундаментальных идеях: во-первых, что отдельные организмы ведут игры с другими организмами своего вида или с членами других видов; во-вторых, что количество генотипов, которые приводят к образованию стратегий, обеспечивающих более высокий выигрыш (более высокий уровень приспособленности), увеличивается, тогда как доля остальных в популяции сокращается. Эти идеи подразумевают ожесточенную борьбу за выживание в том виде, в каком ее подают некоторые интерпретаторы теории Дарвина, которые понимают «выживание самых приспособленных» в буквальном смысле и создали образ «природы с ее законом когтей и клыков». На самом деле в природе немало примеров сотрудничества (когда отдельные животные ведут себя таким образом, что это приносит пользу всей группе) и даже альтруизма (когда отдельные животные несут значительные издержки ради других членов группы). Пчелиный рой и колония муравьев — самые наглядные примеры. Можно ли такое поведение согласовать с эволюционными играми?
Биологи используют классификацию из четырех (фенотипов или генотипов) способов формирования сотрудничества и альтруизма у эгоистичных животных. Ли Дугаткин выделяет четыре категории: 1) семейная динамика; 2) взаимовыгодные сделки; 3) эгоистичное групповое взаимодействие; 4) групповой альтруизм.
Поведение муравьев и пчел — пожалуй, самый доступный для понимания пример семейной динамики. Отдельные члены муравьиной колонии или пчелиного роя близкие родственники, поэтому у них достаточно большое количество общих генов. Все рабочие муравьи в колонии — полные сестры, а значит, у них половина общих генов; выживание и размножение двух сестер способствует размножению генов одного муравья в такой же мере, как и его собственное выживание. Все рабочие пчелы одного роя — полусестры, то есть у них четверть общих генов. Отдельный муравей или пчела не вычисляют, стоит ли рисковать собственной жизнью ради двух сестер, но базовый генотип групп, которые демонстрируют такое поведение (фенотип), будет разрастаться. Мысль о том, что по большому счету эволюция происходит на уровне генов, оказала огромное влияние на биологию, хотя многие неправильно ее истолковали, как произошло в свое время с исходной идеей естественного отбора Дарвина. Интересна идея о том, что так называемый эгоистичный ген может процветать благодаря неэгоистичному поведению в более крупных генных структурах, таких как клетка. Точно так же клетка и ее гены могут процветать за счет кооперативного участия в работе организма и выполнения возложенных на нее задач.
Взаимный альтруизм может возникнуть и между не состоящими в родстве членами одного или разных видов. Такое поведение — это, по сути, пример решения дилеммы заключенных посредством повторения игры, в ходе которой ее участники используют стратегии, поразительно напоминающие стратегию «око за око». Например, некоторые мелкие рыбы или креветки питаются паразитами, которые собираются на зубах и жабрах более крупной рыбы; крупная рыба позволяет мелким рыбешкам заплывать к себе в рот и выполнять «работу чистильщика», не причиняя им вреда. Еще более поразительный, хотя и жуткий пример связан с летучими мышами-вампирами, которые делятся выпитой кровью с теми, у кого охота не задалась. Во время эксперимента, в ходе которого летучих мышей из разных мест обитания объединили в одну группу и некоторых из них лишили пищи, «только летучим мышам, оказавшимся на грани голодания (то есть которые могли погибнуть без пищи в течение двадцати четырех часов), дали свою кровь другие мыши, принимавшие участие в эксперименте. Однако, что еще примечательнее, особи получали кровь только от летучих мышей из своего места обитания… Кроме того, вампиры гораздо чаще отрыгивали кровь, чтобы поделиться ею именно с теми особями из своего места обитания, которые пришли им на помощь, когда они сами в этом нуждались». Опять же, не следует думать, что каждое животное сознательно вычисляет, что отвечает его собственным интересам — продолжение сотрудничества или отказ от него. Напротив, такое поведение носит инстинктивный характер.
Эгоистичное групповое взаимодействие возникает тогда, когда каждый отдельный организм заинтересован в сотрудничестве, если остальные делают то же самое. Другими словами, этот тип кооперативного поведения применим в случае выбора благоприятного исхода в играх в доверие. По мнению Дугаткина, в агрессивной среде популяции более склонны к эгоистичному групповому взаимодействию, чем в более умеренной среде. В неблагоприятных условиях отказ любого члена группы от сотрудничества может закончиться катастрофой для всей группы, в том числе и для уклониста. При таких условиях каждое животное играет важнейшую роль в выживании, поэтому ни один член группы не уклоняется от сотрудничества, если другие несут свою часть общего бремени. В более благоприятной среде каждый может рассчитывать воспользоваться преимуществами, созданными усилиями других членов группы, не подвергая риску выживание всей группы, в том числе и себя самого.
Следующая категория выходит за рамки биологии и распространяется на социологию: организм (а также его клетки и в конечном счете гены) может извлечь пользу из кооперативного поведения в рамках совокупности организмов, а именно общества. Это приводит нас к идее группового альтруизма, которая подразумевает, что определенный уровень сотрудничества должен присутствовать даже между отдельными членами группы, которые не являются близкими родственниками. Нам действительно известны случаи такого поведения. Наглядным примером могут служить группы хищников, таких как волки, и группы человекообразных обезьян, которые часто ведут себя как большие семьи. Сотрудничество возникает даже среди потенциальных жертв, когда отдельные рыбы в косяке по очереди высматривают хищников. Сотрудничество возможно также между разными видами.
Общая идея состоит в том, что группа, члены которой демонстрируют кооперативное поведение, с большей вероятностью добьется успеха во взаимодействии с другими группами, чем группа, члены которой стремятся сыграть роль «безбилетника». Когда в каком-то конкретном контексте эволюционной динамики межгрупповой отбор более сильный фактор, чем внутригрупповой, мы можем наблюдать групповой альтруизм.
Инстинкт заложен в мозге отдельного организма на генетическом уровне, однако взаимность и сотрудничество могут возникнуть как результат целенаправленного мышления или экспериментирования в рамках группы или распространиться не посредством генетики, а путем социализации (с помощью наглядного обучения или наблюдения за действиями старших). Разным видам и ситуациям свойственна своя относительная важность этих двух каналов — природы и воспитания. Можно было бы ожидать, что социализация более важна у людей, но есть примеры ее важной роли и у других животных. Мы хотим привести особенно поразительный пример. В экспедиции Роберта Скотта (1911–1912 годы) на Южный полюс участвовали собаки породы сибирская лайка. Эти собаки, собранные в одну группу и специально подготовленные, за несколько месяцев сформировали поразительную систему сотрудничества и поддерживали ее с помощью схем наказания. «Они чрезвычайно эффективно объединили усилия, направленные против любого члена группы, не желавшего тянуть свою часть ноши, или против того, кто тянул слишком сильно… их методы наказания всегда были неизменны и заканчивались, если их не сдерживать, тем, что они сами, вероятно, назвали бы справедливостью, а мы называем убийством».
Этот воодушевляющий рассказ о том, как кооперативное поведение можно совместить с теорией эволюционных игр, позволяет сделать вывод, что дилемма эгоистичных действий преодолима. На самом деле ученые, изучающие альтруистическое поведение, не так давно сообщили об экспериментальном подтверждении существования такого альтруистического наказания, или сильной взаимности (в отличие от взаимного альтруизма), у людей. Полученные экспериментальные данные свидетельствуют о том, что люди готовы наказывать тех, кто не выполняет свою часть обязанностей в коллективной среде, даже если это сопряжено с определенными издержками и не сулит будущей выгоды. Такая склонность к сильной взаимности может даже помочь объяснить возникновение человеческой цивилизации, если группы с этим качеством обладали более сильной способностью к выживанию в условиях войны и прочих катастроф. Однако, несмотря на все эти выводы, сильная взаимность может не получить широкого распространения в животном мире. «По сравнению с непотизмом, объясняющим сотрудничество муравьев и любого другого существа, заботящегося о подрастающем поколении, примеры взаимности оказались весьма немногочисленными. Вероятно, это вызвано тем, что она требует не только многократных взаимодействий, но и способности распознавать других индивидов, а также “ведения счета” их поступкам». Другими словами, те самые условия, которые, согласно нашему теоретическому анализу, приведенному в , необходимы для решения повторяющейся дилеммы заключенных, по всей вероятности, актуальны и в контексте эволюционных игр.
Резюме
Биологическая теория эволюции в некорых аспектах пересекается с теорией игр, используемой социологами. Эволюционные игры разыгрываются поведенческими фенотипами с генетически предопределенными, а не рационально выбранными стратегиями. В эволюционных играх фенотипы с более высоким уровнем приспособленности выдерживают несколько повторных взаимодействий с другими игроками, с тем чтобы воспроизвести и увеличить свою представленность в популяции. Популяция, содержащая один или более фенотипов в определенных пропорциях, называется эволюционно устойчивой, если ее не могут захватить другие, мутантные, фенотипы или если это ограничивающий исход динамики увеличения численности более приспособленных фенотипов. Если фенотип продолжает доминировать в популяции при столкновении с вторжением мутантного типа, его называют эволюционно устойчивой стратегией, а популяция, состоящая только из этого фенотипа, демонстрирует признаки мономорфизма. Если два или более фенотипа сосуществуют в эволюционно устойчивой популяции, она демонстрирует признаки полиморфизма.
Когда теория эволюционных игр применяется к небиологическим играм, стратегии, которых придерживаются отдельные игроки, считаются стандартными рабочими процедурами или эмпирическими правилами, а не заложенными на генетическом уровне. Процесс воспроизводства выступает в качестве более общих методов передачи информации, таких как социализация, обучение и имитация, а мутации представляют собой экспериментирование с новыми стратегиями.
Эволюционные игры могут иметь структуру выигрышей, аналогичную той, о которой шла речь в и , в том числе в дилемме заключенных и игре в труса. В каждом из этих случаев эволюционно устойчивая стратегия отображает либо равновесие Нэша в чистых стратегиях в соответствующей игре, либо соотношение чистых стратегий в равновесной комбинации в такой игре. В дилемме заключенных эволюционно устойчивая стратегия — «всегда отказ от сотрудничества»; в игре в труса у типов всегда наблюдается более высокий уровень приспособленности, когда их количество ограниченно, поэтому наблюдается полиморфное равновесие; в игре в доверие у немногочисленных типов более низкий уровень приспособленности, поэтому полиморфная конфигурация неустойчива, а равновесия представляют собой крайние варианты. Когда в игру вступают два разных типа представителей каждого из двух разных видов, для определения равновесий используется более сложный анализ, хотя и аналогичным образом структурированный.
Игра «ястреб–голубь» — классический биологический пример; ее анализ сходен с анализом эволюционных версий таких игр, как дилемма заключенных и игра в труса; эволюционно устойчивые стратегии зависят от особенностей структуры выигрышей. Данный анализ можно также выполнить в случае, когда во взаимодействие вступают больше двух типов или когда игра формулируется в общих категориях. Эта теория показывает, что для достижения эволюционной устойчивости необходима равновесная стратегия, эквивалентная равновесию Нэша, которого достигают рациональные игроки.
Ключевые термины
Вторичный критерий
Генотип
Игра «ястреб–голубь»
Игра по всему полю
Мономорфизм
Мутация
Нейтральная эволюционно стабильная стратегия
Отбор
Первичный критерий
Полиморфизм
Приспособленность
Фенотип
Эволюционная стабильность
Эволюционно стабильная стратегия
Упражнения с решениями
S1. Два путешественника покупают одинаковые сувениры ручной работы, упаковывают их в свои чемоданы и отправляются в обратный путь. К сожалению, авиакомпания теряет оба чемодана. Поскольку авиакомпания не знает стоимости потерянных сувениров, она просит путешественников независимо друг от друга ее назвать и соглашается выплатить каждому из них сумму, эквивалентную меньшей из двух названных. Если одно значение будет выше другого, авиакомпания взыщет штраф 20 долларов с того путешественника, который озвучил более высокую цену, и отдаст 20 долларов путешественнику, назвавшему меньшую сумму. Если указанные суммы окажутся равными, не будет ни вознаграждения, ни штрафа. Никто из путешественников не помнит, сколько заплатил за сувенир, поэтому сама цена не имеет значения; каждый просто называет ту, которую предписывает его тип.
Существует два типа путешественников. Тип «высокая стоимость» всегда называет сумму 100 долларов, а тип «низкая стоимость» — 50 долларов. Пусть h — доля в популяции игроков типа «высокая стоимость».
a) Составьте таблицу выигрышей для игры между двумя путешественниками, выбранными из популяции случайным образом.
b) Постройте график уровня приспособленности типа «высокая стоимость», отобразив значения h на горизонтальной оси. На том же рисунке разместите график уровня приспособленности типа «низкая стоимость».
c) Опишите все равновесия в этой игре. По каждому равновесию укажите, оно мономорфное или полиморфное и устойчиво ли оно.
S2. В шла речь о проверке на наличие эволюционно устойчивой стратегии в трижды повторяющейся дилемме заключенных в контексте игры в ценообразование в ресторанах.
a) Воспользовавшись , дайте исчерпывающее объяснение того, почему популяция, состоящая только из игроков типа В, не может быть захвачена ни мутантами типа Н, ни мутантами типа О.
b) Объясните, почему популяция, состоящая только из игроков типа Н, может быть захвачена мутантами типа В и в какой степени ее могут захватить мутанты типа О. Соотнесите это объяснение с представленной в данной главе концепцией нейтральной устойчивости.
c) И наконец, объясните, почему популяция только из игроков типа О не может быть захвачена мутантами типа В, но может быть захвачена мутантами типа Н.
S3. Рассмотрите популяцию, в которой есть два фенотипа: один прирожденный коллективист (ни за что не сознается), второй прирожденный индивидуалист (охотно сознается). При случайном выборе членов этой популяции они получают те же выигрыши в однократной игре, что и выигрыши в представленной ниже . В повторяющемся взаимодействии популяции доступны две стратегии, такие же как в : В (всегда сознаваться) и О (использовать стратегию «око за око», начав с отказа от признания вины).
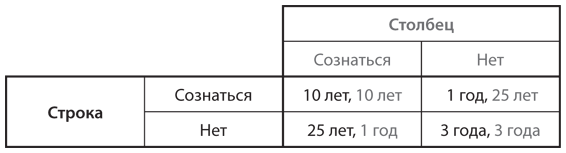
a) Предположим, пара игроков разыгрывает эту дилемму два раза подряд. Составьте для этой дважды повторяющейся дилеммы заключенных таблицу выигрышей.
b) Найдите все эволюционно устойчивые стратегии в этой игре.
c) Теперь прибавьте третью стратегию Н — «никогда не сознаваться». Составьте таблицу выигрышей для этой дважды повторяющейся дилеммы заключенных с тремя возможными стратегиями и найдите все эволюционно устойчивые стратегии новой версии этой игры.
S4. В игре в доверие («место встречи») в данной главе выигрыши отражали некую материальную ценность, получаемую игроками в случае различных исходов; например, это могли быть призы за успешно состоявшуюся встречу. Другие представители этой же популяции, наблюдая за ожидаемыми выигрышами (уровнем приспособленности) двух типов, могли определить, какой из них выше, и со временем имитировать стратегию, обеспечивающую более высокий уровень приспособленности. В итоге соотношение типов в популяции изменилось бы. Однако мы можем представить биологическую интерпретацию этой игры. Предположим, игроки столбца — всегда женского пола, а игроки строки — мужского. Когда два таких игрока встречаются, они вступают в брак, и их дети относятся к тому же типу, что и родители. Таким образом, эти типы могут размножаться или вымереть в зависимости от того, смогут они встретиться или нет. Формальная математика новой версии игры превращает ее в игру между двумя видами (хотя в биологии этого не происходит). Следовательно, доля игроков женского пола типа S (обозначим ее как x) необязательно должна быть равной доле игроков мужского пола типа S (назовем ее y).
a) Проанализируйте динамику изменения значений x и y с помощью методов, аналогичных использованным в данной главе в контексте игры «битва полов».
b) Найдите устойчивый исход или исходы этого динамического процесса.
S5. Вспомните о двух путешественниках из , которые должны назвать цену утерянных сувениров. Допустим, в популяции есть еще и третий фенотип путешественника. Он всегда смешивает стратегии, то есть использует смешанную стратегию, в одних случаях указывая стоимость сувенира 100 долларов, а в других 50 долларов.
a) На основании своих знаний о смешанных стратегиях в рациональных играх предложите смешанную стратегию, которую третий фенотип мог бы использовать в данной игре.
b) Составьте для этой игры таблицу выигрышей три на три, когда третий фенотип использует смешанную стратегию, предложенную вами пункте а.
c) Определите, будет ли смешивающий фенотип эволюционно устойчивой стратегией в данной игре. (Подсказка: проверьте, может ли тип «высокая стоимость» или тип «низкая стоимость» захватить популяцию смешивающего типа.)
S6. Рассмотрите упрощенную модель, в которой все получают электричество либо из солнечной энергии, либо из ископаемого топлива, когда в обоих вариантах присутствует неэластичное предложение. (В случае солнечной энергии будем считать, что это неэластичное предложение необходимого оборудования.) Использование солнечной энергии требует больших первоначальных затрат, поэтому при низкой цене на ископаемое топливо (то есть когда его мало кто использует и существует высокий спрос на оборудование для использования солнечной энергии) они могут оказаться непомерно высокими. Напротив, когда многие используют ископаемое топливо, на него формируется высокий спрос (а значит, и цена), тогда как спрос на солнечную энергию (и ее цена) находится на относительно низком уровне. Предположим, таблица выигрышей двух типов потребителей энергии выглядит следующим образом:
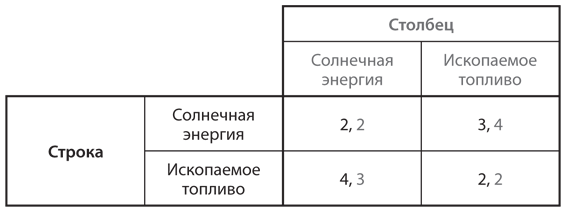
a) Опишите все возможные эволюционно устойчивые стратегии в этой игре относительно доли потребителей солнечной энергии s, а также объясните, почему каждый исход будет устойчивым или неустойчивым.
b) Допустим, в сфере производства оборудования для использования солнечной энергии существует значимая экономия от масштаба, благодаря чему экономия на затратах позволяет повысить выигрыши в ячейке таблицы («солнечная энергия», «солнечная энергия») до (y, y), где y > 2. Насколько большим должно быть значение y, чтобы в полиморфном равновесии s = 0,75?
S7. Существуют два типа участников забега (черепахи и зайцы), которые соревнуются друг с другом выбранными в случайном порядке парами. В этом мире зайцы неизменно побеждают черепах. Если в забеге участвуют два зайца, он заканчивается ничьей, но к концу забега оба зайца совершенно измучены. Когда в забеге участвуют две черепахи, соревнование также заканчивается ничьей, но в его ходе черепахи наслаждаются приятной беседой. Таблица выигрышей выглядит следующим образом (где с > 0):

a) Предположим, доля черепах t в популяции составляет 0,5. При каких значениях c уровень приспособленности черепах будет выше, чем у зайцев?
b) При каких значениях c уровень приспособленности черепах будет выше, чем у зайцев, если t = 0,1?
c) Если c = 1, сможет ли один заяц захватить популяцию, состоящую только из черепах? Объясните, почему да или почему нет.
d) Насколько большим относительно t должно быть значение c в случае черепах, чтобы черепахи были более приспособленными, чем зайцы?
e) Какой уровень t относительно c в полиморфном равновесии? При каких значениях c установится такое равновесие? Обоснуйте свой ответ.
S8. Рассмотрите популяцию с двумя типами X и Y со следующей таблицей выигрышей:
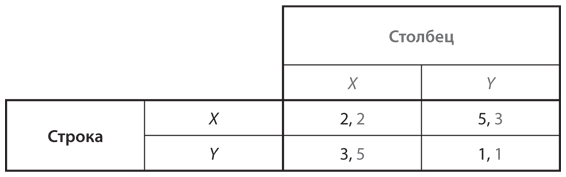
a) Определите уровень приспособленности X как функцию от x, где x — доля X в популяции, а также аналогично уровень приспособленности Y как функцию от y.
Предположим, динамика популяции от поколения к поколению подтверждает следующую модель:
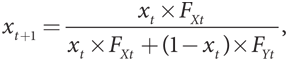
где xt — доля X в популяции за период t; xt+1 — доля X в популяции за период t + 1; FXt — уровень приспособленности X за период t; FYt — уровень приспособленности Y за период t.
b) Предположим, x0, доля X в популяции за период 0, составляет 0,2. Чему равны FX0 и FY0?
c) Найдите значение x1 с помощью значений x0, FX0, FY0 в приведенной выше модели.
d) Чему равны значения FX1 и FY1?
e) Найдите значение x2 (округленное до пяти десятичных знаков).
f) Чему равны значения FX2 и FY2 (округленные до пяти десятичных знаков)?
S9. Рассмотрите эволюционную игру между игроками зеленого и пурпурного типов со следующей таблицей выигрышей:
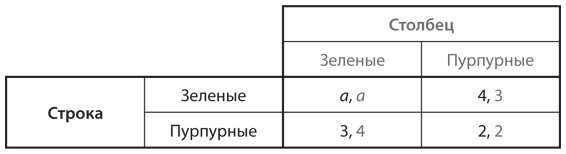
Пусть g — доля зеленых в популяции.
a) Определите уровень приспособленности пурпурного типа через g.
b) Определите уровень приспособленности зеленого типа через g и a.
c) Постройте график приспособленности пурпурного типа относительно доли g пурпурного типа в популяции. Покажите на нем же три линии, отображающие уровень приспособленности зеленых при a = 2, 3 и 4. Какой вывод на основании этого графика вы можете сделать о диапазоне значений а, обеспечивающих устойчивое полиморфное равновесие?
d) Допустим, значение а попадает в диапазон, найденный в пункте с. Чему равна доля зеленых g относительно a в случае устойчивого полиморфного равновесия?
S10. Докажите следующее утверждение: «Если стратегия строго доминирующая согласно таблице выигрышей в игре с участием рациональных игроков, то в эволюционной версии той же игры она исчезнет, каким бы ни был исходный состав популяции. Если стратегия слабо доминируемая, она сможет сосуществовать с некоторыми другими типами, но не в случае смешения всех типов».
Упражнения без решений
U1. Рассмотрите игру в выживание, в которой представители большой популяции животных встречаются друг с другом и либо вступают в схватку, либо делят между собой источник пищи. В популяции есть два фенотипа: один всегда дерется, а другой всегда делится пищей. Будем исходить из того, что в популяции не могут появиться другие мутантные типы. Предположим, ценность источника пищи составляет 200 калорий и калорийность пищи определяет репродуктивную приспособленность каждого игрока. Если встречаются два типа, которые делятся пищей, каждый из них получает половину, но если игрок, который делится пищей, встречается с тем, кто всегда дерется, он сразу же уступает и задира получает всю пищу.
a) Допустим, издержки в случае драки (для каждого игрока) составляют 50 калорий, а когда встречаются два драчуна, каждый из них с равной вероятностью может либо победить в схватке и получить всю пищу, либо проиграть и вообще остаться без еды. Составьте таблицу выигрышей в игре с участием двух игроков, выбранных из популяции случайным образом. Найдите в этой популяции все эволюционно устойчивые стратегии. К какому типу можно отнести игру в данном случае?
b) Теперь предположим, что издержки в случае драки составляют 150 калорий. Составьте таблицу выигрышей и найдите все эволюционно устойчивые стратегии в популяции в этой ситуации. Какой тип игры будет в данном случае?
c) Воспользовавшись системой обозначений из игры «ястреб–голубь» данной главы, укажите значения V и C в пунктах a и b и покажите, что ваши ответы в этих пунктах согласуются с анализом, представленным в данной главе.
U2. Допустим, в однократной игре «дилемма заключенных» следующая таблица выигрышей:
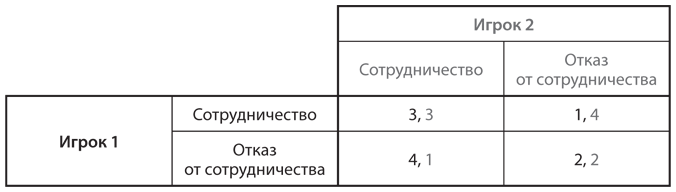
В большой популяции, в которой поведение каждого члена генетически предопределено, каждый игрок будет либо всегда отказываться от сотрудничества в любой игре «дилемма заключенных», либо использовать стратегию «око за око». (В дилемме заключенных, состоящей из нескольких раундов, этот игрок выбирает сотрудничество в первом раунде, а в каждом последующем делает то, что сделал соперник в предыдущем раунде игры.) Пары случайным образом выбранных из популяции игроков сыграют серии из n отдельных раундов этой дилеммы (при n ≥ 2). Выигрыш каждого игрока в одной полной серии (состоящей из n раундов игры) равен сумме выигрышей в n раундах.
Пусть p — доля игроков, всегда отказывающихся от сотрудничества, а (1 – p) — доля игроков, всегда выбирающих стратегию «око за око». Каждый член популяции неоднократно играет в таких сериях дилемм, каждый раз против нового, выбранного случайным образом соперника. Игрок, использующий стратегию «око за око», всегда начинает новую серию с сотрудничества в первом раунде игры.
a) В таблице два на два покажите выигрыши игрока каждого типа в случае, если в ходе одной серии каждый игрок вступает в противостояние с соперником каждого из двух типов.
b) Определите уровень приспособленности (средний выигрыш в одной серии против случайно выбранного соперника) игрока, который всегда отказывается от сотрудничества.
c) Определите уровень приспособленности игрока, всегда выбирающего стратегию «око за око».
d) На основании ответов в пунктах b и c докажите, что при p > (n – 2) / (n – 1) тип, всегда отказывающийся от сотрудничества, имеет более высокий уровень приспособленности, а при p < (n – 2) / (n – 1) более высокий уровень приспособленности у типа, всегда выбирающего стратегию «око за око».
e) Если эволюция приводит к постепенному увеличению доли более приспособленного типа в популяции, каковы возможные равновесные исходы этого процесса для популяции, о которой идет речь в упражнении? (Другими словами, каковы возможные эволюционно устойчивые равновесия?) Проиллюстрируйте свой ответ с помощью графика уровней приспособленности.
f) В каком смысле большее количество повторений (более высокие значения n) способствует эволюции сотрудничества?
U3. Предположим, в дважды повторяющейся дилемме заключенных из в популяции может существовать четвертый тип (тип С). Он не признает своей вины в первом раунде, но сознается во втором раунде каждого эпизода в двух подряд раундах игры против того же соперника.
a) Составьте таблицу уровней приспособленности четыре на четыре в этой игре.
b) Может ли новый тип С выступать в качестве эволюционно устойчивой стратегии данной игры?
c) В игре с тремя типами из типы В и О были эволюционно устойчивыми стратегиями, но тип О был нейтрально устойчивым, поскольку с ним могла сосуществовать небольшая доля мутантов Н. Докажите, что тип О не может быть эволюционно устойчивой стратегией в игре с четырьмя типами.
U4. Придерживаясь схемы, описанной в , проанализируйте эволюционную версию игры в розыгрыш очка в теннисе (см. ). Рассматривая подающих и принимающих игроков как отдельные виды, постройте рисунок, аналогичный . Что вы можете сказать об эволюционно устойчивой стратегии и ее динамике?
U5. Вспомните о популяции животных из , борющихся за источник пищи, ценность которого составляет 200 калорий. Предположим, что в пункте b этого упражнения издержки в случае драки (для каждого игрока) равны 150 калорий. Представим также, что в этой популяции есть третий фенотип, который всегда смешивает стратегии, то есть использует смешанную стратегию, порой вступая в драку, а порой делясь пищей с другими.
a) На основании своих знаний о смешанных стратегиях в рациональных играх предложите разумную смешанную стратегию, которую третий фенотип мог бы использовать в данной игре.
b) Составьте таблицу выигрышей три на три для этой игры, когда третий фенотип использует смешанную стратегию, предложенную вами в пункте а.
c) Определите, будет ли смешивающий фенотип эволюционно устойчивой стратегией в данной игре. (Подсказка: проверьте, может ли тип, который всегда вступает в драку, или тип, который всегда делится пищей, захватить популяцию смешивающего типа.)
U6. Рассмотрим эволюционную версию игры между Бейкером и Катлером из . В этот раз Бейкер и Катлер — не два человека, а два разных вида. Каждый раз при встрече они ведут следующую игру. Бейкер выбирает общий приз в размере 10 или 100 долларов. Катлер решает, как разделить приз, выбранный Бейкером; при этом Катлер может разделить приз либо в соотношении 50 на 50, либо в соотношении 90 на 10 в свою пользу. Катлер ходит первым, а Бейкер вторым.
В популяции есть два типа Катлеров: тип F выбирает справедливое разделение приза (50 на 50), тогда как тип G — корыстное разделение (90 на 10). Существует также два типа Бейкеров: тип S просто выбирает большой приз (100 долларов) независимо от действий Катлера, тогда как тип T выбирает большой приз (100 долларов), но при условии, что Катлер его разделит 50 на 50, и маленький приз (10 долларов), если Катлер выберет разделение 90 на 10.
Пусть f — доля типа F в популяции Катлеров, а значит, (1 – f) — доля в этой популяции типа G. Пусть s — доля типа S в популяции Бейкеров, а значит, (1 – s) — доля в этой популяции типа T.
a) Определите уровень приспособленности типов F и G относительно s.
b) Определите уровень приспособленности типов S и T относительно f.
c) При каком значении s у типов F и G одинаковый уровень приспособленности?
d) При каком значении f у типов S и T одинаковый уровень приспособленности?
e) На основании полученных выше ответов начертите график динамики популяций. Отобразите значения f на горизонтальной оси, а значения s — на вертикальной.
f) Опишите все равновесия в этой эволюционной игре, а также укажите эволюционно устойчивые равновесия.
U7. Вспомните . Как оказалось, зайцы весьма заносчивые победители. Каждый раз, когда они обгоняют черепах, они безжалостно высмеивают их медлительность. Бедные черепахи не только проигрывают забег, но и терпят оскорбления со стороны зайцев. Таблица выигрышей в этой игре выглядит так:

a) При каких значениях c уровень приспособленности черепах будет выше, чем у зайцев, если доля черепах t в популяции составляет 0,5? Чем этот результат отличается от ответа, полученного в ?
b) При каких значениях c уровень приспособленности черепах будет выше, чем у зайцев, если t = 0,1? Чем этот результат отличается от ответа, полученного в ?
c) Если c = 1, сможет ли один заяц захватить популяцию, состоящую только из черепах? Объясните, почему да или почему нет.
d) Насколько большим относительно t должно быть значение c в случае черепах, чтобы они были более приспособленными, чем зайцы?
e) Какой уровень t относительно c в полиморфном равновесии? При каких значениях c установится такое равновесие? Обоснуйте свой ответ.
f) Будет ли устойчивым полиморфное равновесие, найденное в пункте e? Почему да или почему нет?
U8 (рекомендуется использовать электронную таблицу). В данной задаче выполняется более глубокий анализ динамики популяции от поколения к поколению, о которой шла речь в . Поскольку математические расчеты могут быстро стать достаточно сложными и громоздкими, рекомендуем выполнить этот анализ с помощью электронной таблицы.
Опять же, рассмотрим популяцию с двумя типами X и Y со следующей таблицей выигрышей:

Вспомните, что динамику популяции от поколения к поколению определяет следующая формула:
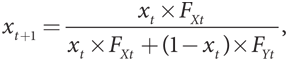
где xt — доля X в популяции за период t; xt+1 — доля X в популяции за период t + 1; FXt — уровень приспособленности X за период t; FYt — уровень приспособленности Y за период t.
С помощью электронной таблицы расширьте область этих вычислений на большее количество поколений. (Подсказка: расположите значения xt, FXt и FYt в трех смежных горизонтальных ячейках таблицы, а в каждой следующей строке пусть будут представлены периоды [t = 0, 1, 2, 3, …]. Используйте формулы электронной таблицы, для того чтобы соотнести FXt и FYt c xt и xt+1 в соответствии с представленной моделью динамики популяции.)
a) Если в период 1 (другими словами, когда x0 = 0,5) в популяции имеет место равное соотношение X и Y, какой будет доля X в следующем поколении, то есть x1? Чему равны значения FX1 и FY1?
b) С помощью электронной таблицы выполните соответствующие вычисления для очередного поколения, затем для следующего и т. д. Чему равно значение x20 с точностью до четырех десятичных знаков? Чему равны значения FX20 и FY20?
c) Определите x*— равновесный уровень x. Через сколько поколений популяция будет находиться в пределах 1 процента от x*?
d) Ответьте на вопрос в пункте b при x0 = 0,1.
e) Выполните задание в пункте b при x0 = 1.
f) Выполните задание в пункте b при x0 = 0,99.
g) Возможны ли мономорфные равновесия в данной модели? Если да, устойчивы ли они? Обоснуйте свой вывод.
U9. Рассмотрите эволюционную игру между игроками зеленого и пурпурного типов со следующей таблицей выигрышей:

С учетом параметров a, b, c, d определите условия, которые обеспечивают устойчивое полиморфное равновесие.
U10 (дополнительное упражнение для студентов с хорошей математической подготовкой). Пусть в эволюционной игре с тремя типами, представленной в и на , q3 = 1 – q1 – q2 — доля агрессивных оранжевогорлых игуан. В таком случае динамику изменения доли каждого типа игуан в популяции можно описать так:
q1 увеличивается тогда и только тогда, когда –q2 + q3 > 0,
q2 увеличивается тогда и только тогда, когда q1 – q3 > 0.
Хотя это и не было оговорено в явном виде в , но аналогичное правило для q3 выглядит так:
q3 увеличивается тогда и только тогда, когда – q1 + q2 > 0.
a) Выполните более подробный анализ этой динамики. Пусть скорость изменения переменной x во времени t обозначается посредством производной dx/dt. Далее предположим, что
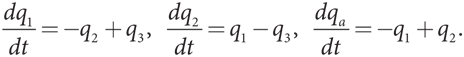
Проверьте, подтверждают ли эти производные сформулированные выше утверждения в отношении динамики популяции.
b) Определим X = (q1)2 + (q2)2 + (q3)2. С помощью формул дифференцирования сложных функций покажите, что dX/dt = 0, иными словами, продемонстрируйте, что значение X остается постоянным по времени.
c) Мы знаем, что q1 + q2 + q3 = 1. Используя этот факт в совокупности c результатом из пункта b, покажите, что с течением времени точка (q1, q2, q3) движется в трехмерном пространстве по кругу.
d) Говорит ли ответ, полученный в пункте c, об устойчивости эволюционной динамики в популяции пятнистобоких игуан?

