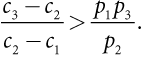13 Разработка механизмов для задачи «принципал–агент»
В 1996 году Джеймс Миррлис получил Нобелевскую премию по экономике за новаторскую работу по оптимальному нелинейному налогообложению доходов и связанным с ним политическим вопросам. Многие неэкономисты и некоторые экономисты нашли ее трудной для понимания. Однако журнал Economist дал ей блестящую характеристику, подчеркнув ее важность и значимость, а также отметив, что Миррлис показал, «как иметь дело с тем, кто знает больше вас».
В мы уже видели, как асимметричная информация влияет на анализ игры. Но основная задача, которую пытался решить Миррлис, несколько отличалась от ситуаций, рассмотренных нами ранее. В его работе одному игроку (правительству) требовалось составить такой свод правил, при котором стимулы другого игрока (налогоплательщика) соответствовали бы целям первого игрока. В настоящее время модели, применимые к широкому спектру социальных и экономических взаимодействий и основанные на общей концептуальной схеме, в соответствии с которой менее информированный игрок выполняет действия, выгодные для более информированного игрока, существуют в большом количестве. Обычно менее информированного игрока называют принципалом, а более информированного — агентом; соответственно, такие модели обозначаются термином «модель “принципал–агент”». Сам процесс, используемый принципалом для создания правильного набора стимулов для агента, известен как разработка механизмов.
В модели Миррлиса правительство пытается найти баланс между эффективностью и справедливостью; оно хочет, чтобы более продуктивные члены общества вкладывали усилия в увеличение общего объема производства, после чего правительство бы перераспределяло доходы в пользу неимущих. Если бы ему была точно известна потенциальная производительность каждого человека и оно могло бы отслеживать количество и качество вложенных усилий, каждый член общества просто был бы обязан трудиться в соответствии со своими возможностями, а плоды его труда распределялись бы согласно потребностям людей. Но сбор столь подробной информации слишком дорогостоящий, если вообще возможен, кроме того, не меньше трудностей возникло бы с практической реализацией таких схем перераспределения. Каждый человек прекрасно знает свои способности и потребности, поэтому выбирает собственный уровень усилий, но ему выгоднее скрывать эту информацию от правительства. Когда человек делает вид, что у него меньше способностей и больше потребностей, это позволяет ему выплачивать меньше налогов или получать помощь от правительства; при этом стимул вкладывать усилия ослабевает, когда правительство забирает часть дохода. Правительство должно просчитывать свою налоговую политику или разрабатывать налогово-бюджетный механизм с учетом всех этих нюансов с информацией и стимулами. Миррлису удалось решить сложную задачу разработки механизмов в рамках концептуальной схемы «принципал–агент».
Экономист Уильям Викри разделил с Миррлисом Нобелевскую премию по экономике 1996 года, получив ее за разработку механизмов при наличии асимметричной информации. Наибольшую известность Викри принесла разработка алгоритма проведения аукциона, стимулирующего участников делать ставки по истинной стоимости выставленного на продажу объекта (эту тему мы подробно изучим в ). Однако исследования Викри распространяются и на другие механизмы, такие как система дорожных сборов в период пиковой нагрузки (он и Миррлис заложили основу для обширных изысканий в данной области).
Примечательно, что за последние тридцать лет общая теория разработки механизмов получила серьезное развитие. За сделанный в нее вклад Леониду Гурвицу, Роджеру Майерсону и Эрику Маскину в 2007 году была присуждена Нобелевская премия по экономике. Они и многие другие ученые применили данную теорию во множестве разных областей, таких как системы оплаты труда, страховые полисы и, разумеется, шкала налогообложения и аукционы. В этой главе мы проанализируем несколько известных сфер применения теории разработки механизмов, воспользовавшись нашим обычным методом числовых примеров и упражнений.
1. Ценовая дискриминация
Как правило, компания продает свою продукцию различным клиентам с разными уровнями готовности платить. Теоретически она хотела бы получать от каждого клиента максимум, который он готов заплатить. Если бы компания действительно могла назначать каждому клиенту индивидуальную цену, соответствующую его готовности платить, экономисты сказали бы, что она практикует совершенную ценовую дискриминацию, или ценовую дискриминацию первой степени.
Однако совершенная ценовая дискриминация может оказаться невозможной по многим причинам. Самая общая состоит в том, что даже клиент, который готов заплатить много, предпочитает платить меньше. Следовательно, он выберет более низкую цену, и не исключено, что компании придется конкурировать с другими компаниями или торговыми посредниками, которые сбивают ее высокую цену. Но даже при отсутствии прямых конкурентов компания, как правило, не знает, сколько каждый отдельный клиент готов заплатить, поэтому клиенты попытаются сделать вид, что не намерены платить высокую цену, чтобы добиться более низкой цены. Иногда, даже если компания смогла определить готовность платить, может быть незаконно использовать явную дискриминацию первой степени на основании отличительных характеристик клиента. В подобных ситуациях компания должна разработать такую линию продуктов и цен, чтобы выбор клиентами того, что они покупают (а значит, и за что платят), хотя бы в какой-то мере соответствовал ее целям по увеличению прибыли путем ценовой дискриминации.
В терминологии игр с асимметричной информацией, используемой нами в , процесс, посредством которого компания определяет готовность клиента платить на основании решений о покупке, подразумевает скрининг в целях разделения типов (путем самоотбора). Компания не знает тип каждого клиента (его готовность платить), поэтому пытается получить эту информацию, анализируя его действия. Подход, применяемый для этого авиакомпаниями, — общеизвестный пример. Авиакомпании стараются отделить бизнес-пассажиров, готовых заплатить больше, от туристов, более чувствительных к цене билетов, предлагая низкие цены в обмен на различные ограничения на тарифы, неприемлемые для пассажиров бизнес-класса, такие как требования предварительной оплаты и минимальные условия комфорта. Мы проанализируем этот пример более подробно, чтобы уточнить все эти идеи, сделав их поддающимися количественному определению.
Рассмотрим решения по установлению цен, которые принимает PieInTheSky (PITS) — авиакомпания, обслуживающая маршрут из Поданка в Южную Саккоту; ее самолеты перевозят определенное количество бизнес-пассажиров и определенное количество туристов. За любое место, указанное в авиабилете, пассажиры первого типа готовы платить более высокую цену, чем второго. Для того чтобы с выгодой для себя обслужить туристов, не назначая при этом низкую цену пассажирам, совершающим деловые поездки, компания PITS должна найти способ создания разных версий одного и того же рейса. Кроме того, ей необходимо установить такие цены на билеты, чтобы эти два типа пассажиров выбрали разные варианты. Как уже отмечалось выше, авиаперевозчик может провести различие между двумя типами пассажиров, предложив им тарифы с ограничениями и без. Практика продажи билетов в салоны первого и экономкласса — еще один способ разграничить две группы пассажиров (именно ее мы используем в нашем примере).
Предположим, 30% клиентов авиакомпании PITS — бизнесмены, а 70 — туристы. В таблице на рис. 13.1 показана максимальная готовность каждого из двух типов клиентов платить за каждую категорию обслуживания плюс затраты на предоставление им услуг, а также потенциальная прибыль, которую можно получить в каждом случае.
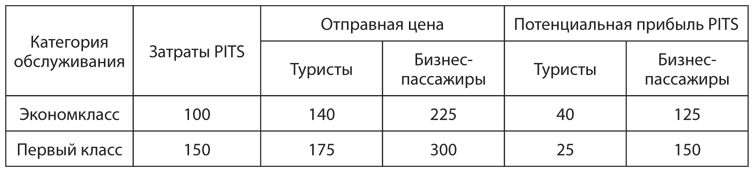
Рис. 13.1. Ценовая дискриминация в авиакомпании
Начнем с разработки наилучшей с точки зрения авиаперевозчика системы определения цен на билеты. Допустим, авиакомпании известен тип каждого отдельного клиента; скажем, продавцы определяют его по одежде клиентов, когда те приходят бронировать места. Будем также исходить из того, что не существует правовых запретов на дифференцированное ценообразование и нет возможности перепродать более дешевые билеты другим пассажирам. (Реальные авиакомпании предотвращают такую перепродажу посредством требования о достоверной идентификации каждого пассажира, имеющего билет.) При таких условиях компания PITS могла бы применить совершенную ценовую дискриминацию (ценовую дискриминацию первой степени).
Какую цену назначила бы при этом компания PITS клиентам каждого типа? Она могла бы продать билет каждому бизнесмену в салон первого класса за 300 долларов с прибылью 300 – 150 = 150 долларов на один билет или продать ему же билет в салон экономкласса за 225 долларов с прибылью 225 – 100 = 125 долларов на один билет. Первый вариант выигрышнее для PITS, поэтому она захотела бы продавать бизнес-пассажирам билеты в салон первого класса по 300 долларов. Каждому туристу авиакомпания могла бы продать билет в салон первого класса за 175 долларов с прибылью 175 – 150 = 25 долларов или билет в салон экономкласса за 140 долларов с прибылью 140 – 100 = 40 долларов. В этом случае для PITS лучше второй вариант, поэтому она захотела бы продавать туристам билеты в салон экономкласса по 140 долларов. Следовательно, в идеале компания PITS предпочла бы продавать билеты первого класса только пассажирам, совершающим деловые поездки, и билеты экономкласса только туристам, в каждом случае по цене, эквивалентной максимальной готовности соответствующей группы пассажиров платить. Общий объем прибыли PITS, полученной за счет этой стратегии в расчете на 100 клиентов, составил бы:
(140 – 100) × 70 + (300 – 150) × 30 = 40 × 70 + 150 × 30 = 2800 + 4500 = 7300.
Таким образом, наилучший для PITS исход обеспечивает ей прибыль 7300 долларов на каждых 100 пассажиров, которых она обслуживает.
Теперь вернемся к более реалистичному сценарию, в соответствии с которым PITS не может определить тип каждого клиента или не имеет права задействовать эту информацию в целях явной ценовой дискриминации. Как авиакомпания может использовать разные варианты билетов для скрининга своих клиентов?
Первое, что необходимо понять авиаперевозчику, что разработанная выше система ценообразования далеко не самая прибыльная при отсутствии идентифицирующих данных о каждом клиенте. И самое главное — компания не может назначить бизнес-пассажирам максимальную цену в размере 300 долларов, которую они готовы заплатить за места в салоне первого класса, при цене 140 долларов за билет в экономкласс. Ведь тогда бизнесмены могли бы купить билеты в экономкласс, за которые они готовы заплатить 225 долларов, и получить при этом дополнительную выгоду, или, на языке экономистов, излишек потребителя, в размере 225 – 140 = 85 долларов, который они могли бы использовать, скажем, на оплату более качественного питания или проживания во время поездки. А максимальная цена 300 долларов не обеспечивает им излишка потребителя, поэтому они предпочли бы билеты экономкласса. Следовательно, в данной ситуации скрининг окажется бесполезным. Прибыль компании PITS в расчете на 100 клиентов упала бы до (140 – 100) × 100 = 4000 долларов.
Максимальная цена, которую PITS сможет назначить за билеты в салон первого класса, должна гарантировать бизнес-пассажирам дополнительную выгоду, не меньше чем 85 долларов, которые они получили бы, купив билет в экономкласс. Стало быть, цена билетов первого класса может составлять максимум 300 − 85 = 215 долларов. (Возможно, следовало бы назначить цену 214 долларов, чтобы дать бизнес-пассажирам однозначный положительный стимул выбрать первый класс, но мы не будем принимать во внимание столь несущественную разницу.) Компания PITS по-прежнему может установить цену 140 долларов на билеты экономкласса, для того чтобы получить максимальную прибыль за счет туристов, поэтому общий объем ее прибыли (на 100 клиентов) при этом составит:
(140 – 100) × 70 + (215 – 150) × 30 = 40 × 70 + 65 × 30 = 2800 + 1950 = 4750.
Эта прибыль больше 4000 долларов, которые авиакомпания получила бы вследствие безуспешной реализации схемы совершенной ценовой дискриминации в условиях ограниченной информации, но меньше 7300 долларов, которые ей удалось бы получить при наличии полной информации и успешном применении совершенной ценовой дискриминации.
Установив на билеты первого класса цену 215 долларов, а на билеты экономкласса 140 долларов, компания PITS может без проблем выполнить скрининг и разделить пассажиров на два типа на основании их самостоятельного выбора одного из двух видов обслуживания. Однако ради достижения такой косвенной ценовой дискриминации PITS должна пожертвовать частью прибыли, которую она потеряет из-за необходимости назначить бизнес-клиентам цену, меньшую, чем та, которую они готовы заплатить. В итоге прибыль PITS в расчете на 100 клиентов сократится с 7300 долларов, которую компания могла бы иметь в случае прямой ценовой дискриминации при наличии исчерпывающей информации о типе каждого клиента, до 4750 долларов в случае косвенной дискриминации, основанной на самоотборе. Разница в 2550 долларов в точности равна 85 × 30, где 85 — сумма снижения цен на билеты первого класса по отношению к цене, которую бизнес-пассажиры готовы за них заплатить, а 30 — количество бизнес-пассажиров на 100 обслуженных пассажиров.
Согласно нашему анализу, авиакомпании PITS придется поддерживать цены на билеты первого класса на достаточно низком уровне, чтобы бизнес-пассажиры были заинтересованы в выборе данного класса обслуживания. У них есть вариант предпочесть экономкласс, если это обеспечит им более весомую выгоду (или излишек), поэтому компании PITS необходимо найти способ удержать их от этого шага. Такое требование, или ограничение в отношении стратегии скрининга, возникает во всех задачах, связанных с разработкой механизмов, и обозначается термином ограничение совместимости стимулов.
Единственное, что позволит компании PITS назначить бизнес-пассажирам цену на билеты первого класса более 215 долларов, не спровоцировав их переход на другой класс обслуживания, — это повышение тарифа на билеты экономкласса. Например, если стоимость билета первого класса составляет 240 долларов, а экономкласса — 165 долларов, бизнес-пассажиры получат одинаковую дополнительную выгоду (излишек потребителя) при покупке билетов обоих классов: 300 — 240 долларов в случае билета первого класса и 225 — 165 долларов в случае билета экономкласса. Следовательно, они предпочтут первый класс, или по 60 долларов в каждом случае. При таких более высоких ценах бизнес-пассажиры по-прежнему готовы покупать билеты только в салон первого класса, что позволит компании PITS получить более высокую прибыль с каждого билета.
Однако цена билетов экономкласса в размере 140 долларов — предельная сумма, которую готовы заплатить туристы. Если компания PITS поднимет ее, скажем, до 165 долларов, она вообще потеряет клиентов этого типа. Для того чтобы сохранить их готовность покупать билеты, механизм ценообразования, используемый PITS, должен удовлетворять еще одному условию — условию ограничения участия.
Таким образом, стратегия ценообразования, применяемая компанией PITS, находится между двумя ограничениями: ограничением участия туристов и ограничением совместимости стимулов бизнес-пассажиров. Если компания назначит цену X на билеты экономкласса и цену Y на билеты первого класса, она должна обеспечить выполнение условия X < 140, для того чтобы билеты покупали туристы, и условия 225 – X < 300 – Y, или Y < X + 75, чтобы бизнес-пассажиры выбирали первый, а не экономкласс. Вследствие таких ограничений PITS стремится установить как можно более высокие цены. Следовательно, скрининговая стратегия компании, направленная на максимизацию прибыли, сводится к тому, чтобы сделать значение X как можно более близким к 140 долларам, а значение Y как можно более близким к 215 долларам. Исключив из рассмотрения небольшие различия, необходимые для сохранения знака <, будем исходить из того, что цены на билеты составляют 140 и 215 долларов. В таком случае назначение цены 215 долларов на билеты первого класса и 140 долларов на билеты экономкласса и есть решение задачи PITS по разработке механизма ценообразования.
Оптимальна ли эта стратегия для авиакомпании, зависит от конкретных данных, используемых в этом примере. Если бы доля бизнес-пассажиров была значительно больше, например 50%, PITS пришлось бы пересмотреть оптимальные цены на билеты. Если 50% ее клиентов составляют пассажиры, совершающие деловые поездки, убытки в размере 85 долларов на каждом бизнес-пассажире могут оказаться слишком высокими, чтобы оправдать сохранение немногочисленных туристов. Возможно, PITS было бы лучше вообще отказаться от обслуживания клиентов этой категории, то есть нарушить условие ограничения участия туристов ради повышения стоимости первого класса обслуживания. В действительности стратегия ценовой дискриминации посредством скрининга при таком соотношении пассажиров разных типов обеспечивает компании PITS следующую прибыль (в расчете на 100 клиентов):
(140 – 100) × 50 + (215 – 150) × 50 = 40 × 50 + 65 × 50 = 2000 + 3250 = 5250.
Стратегия обслуживания только бизнес-пассажиров посредством продажи им билетов по цене 300 долларов гарантирует компании PITS более высокую прибыль (в расчете на 100 клиентов), чем при использовании инструмента скрининга:
(300 – 150) × 50 = 150 × 50 = 7500.
Таким образом, при наличии относительно небольшого количества клиентов с готовностью платить более низкую цену продавец может предпочесть вообще не обслуживать их, чем предлагать достаточно низкие цены множеству клиентов, готовых заплатить высокую цену, чтобы предотвратить их переход на недорогую версию продукта.
Какая именно доля бизнес-пассажиров занимает промежуточную позицию между этими двумя случаями? Мы предоставляем возможность решить эту задачу вам. Нам же остается заметить, что решение авиакомпании снизить тарифы для туристов может быть ее ответом на асимметричность информации, а не признаком особой привязанности к отпускникам!
2. Некоторые термины
Итак, мы увидели один пример разработки механизмов в действии. Безусловно, есть еще масса других примеров, и мы расскажем о некоторых из них в следующих разделах. А пока сделаем небольшую паузу, чтобы представить несколько специальных терминов, используемых в большинстве подобных моделей.
Существует два широких класса проблем, связанных с разработкой механизмов. Первый, аналогичный ситуации с ценовой дискриминацией в приведенном выше примере, состоит в том, что один игрок лучше информирован (в нашем примере клиент знает свою готовность платить) и от этой информации зависит выигрыш другого игрока (установление цен авиакомпанией, а значит, и ее прибыль). Менее информированный игрок разрабатывает схему, в соответствии с которой более информированный игрок должен сделать выбор, раскрывающий эту информацию, хотя это и повлечет за собой определенные издержки для первого (в нашем примере отсутствие возможности назначить бизнес-пассажирам цену, соответствующую их максимальной готовности платить).
Второй класс проблем разработки механизмов касается действий, предпринимаемых одним игроком, которые не могут отслеживать другие игроки. Например, работодатель не может видеть качество, а порой даже количество усилий, вкладываемых работником; у страховой компании нет возможности отслеживать действия, предпринимаемые застрахованным водителем или домовладельцем для снижения риска аварии или ограбления. В терминах, представленных в , эта проблема обозначается как моральный риск. Менее информированный игрок разрабатывает схему (например, участие в прибылях для работника или нестрахуемый минимум и участие в оплате при страховании), которая в определенной степени приводит стимулы другого игрока в соответствие со стимулами ее автора.
В каждом из этих случаев механизм разрабатывает менее информированный игрок, которого в стратегической игре называют принципалом. Более информированного игрока называют агентом, что точно отображает суть происходящего в отношении работника, но не столь точно в случае клиента. Тогда данную игру можно назвать проблемой «принципал–агент», или агентской проблемой.
Принципал разрабатывает механизм максимизации своего выигрыша при наличии двух ограничений. Во-первых, ему известно, что агент использует этот механизм для максимального увеличения своего выигрыша (выигрыша агента). Иными словами, механизм принципала должен соответствовать стимулам агента. Как мы уже говорили в , это условие обозначается термином «ограничение совместимости стимулов». Во-вторых, учитывая, что агент реагирует на этот механизм исходя из собственных интересов, агентские отношения должны обеспечивать ему как минимум такую же ожидаемую полезность, как он бы получил в другом месте, например работая на другого работодателя или отправившись в путешествие на автомобиле вместо самолета. В мы обозначили это условие термином «ограничение участия». В ситуации с ценовой дискриминацией в авиакомпании мы видели конкретные примеры этих двух условий; другие примеры и сферы применения будут представлены в следующих разделах данной главы.
3. Контракты «затраты плюс» и контракты с фиксированной ценой
При составлении закупочных контрактов на получение определенных услуг вроде строительства скоростной автомагистрали или офисного здания правительства или компании сталкиваются с теми же проблемами разработки механизмов, которые мы рассматриваем в данной главе. Есть два распространенных типа таких контрактов — «затраты плюс прибыль» и «фиксированная цена». В случае первого поставщик услуг получает сумму, эквивалентную его затратам, плюс вознаграждение в размере нормальной прибыли. В контракте с фиксированной ценой заранее оговаривается конкретная цена услуг, при этом их поставщик оставляет себе всю сверхприбыль, если его фактические затраты меньше ожидаемых, и несет убытки, если фактические затраты оказываются выше.
Каждый тип контракта имеет свои достоинства и недостатки. Контракт «затраты плюс» не обеспечивает подрядчику сверхприбыль; этот аспект особенно важен для государственных контрактов на закупку, где в конечном счете именно граждане оплачивают закупленные услуги. Однако поставщик, как правило, лучше информирован о своих затратах, чем покупатель услуг, поэтому у поставщика может возникнуть желание завысить объем затрат или увеличить их, чтобы извлечь для себя выгоду из необоснованно высоких расходов. Напротив, контракт с фиксированной ценой дает поставщику услуг все стимулы удерживать затраты на минимальном уровне, а значит, и обеспечивать эффективное использование ресурсов. Но при таком типе государственных контрактов обществу приходится платить установленную цену и отдавать поставщику услуг сверхприбыль. Оптимальный механизм закупок должен учитывать оба аспекта.
А. Строительство автомагистрали: полная информация
Рассмотрим пример разработки правительством штата механизма закупок в рамках проекта дорожного строительства. Предположим, планируется построить автомагистраль с привлечением местного дорожного подрядчика и органам власти штата необходимо решить, сколько на ней должно быть полос. Чем больше полос, тем больше пользы в виде более быстрого передвижения и меньшего количества аварий (во всяком случае до уровня, превышение которого нанесет чрезмерный ущерб сельской местности). Мы будем исходить из того, что социальная стоимость V (исчисляемая в миллиардах долларов) от наличия N полос на автомагистрали определяется следующей формулой:
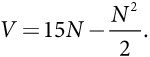
Стоимость строительства одной полосы, в том числе вознаграждение в размере нормальной прибыли, могло бы составить либо 3, либо 5 миллиардов долларов в зависимости от типа грунта на строительном участке. На данный момент будем считать, что правительство штата может определить объем затрат на строительство так же, как и подрядчик. В итоге оно выбирает количество полос N и составляет контракт таким образом, чтобы максимально увеличить выгоду для штата (V) за вычетом вознаграждения подрядчику (назовем его F), то есть цель правительства штата — максимизировать свою чистую выгоду G, где G = V – F.
Допустим, властям штата известно, что фактический объем затрат составляет 3 (миллиарда долларов на одну полосу автомагистрали), следовательно, подрядчику придется выплатить 3N за строительство автомагистрали, состоящей из N полос. Далее правительство выбирает такое значение N, которое обеспечивает чистую выгоду G согласно следующей формуле:
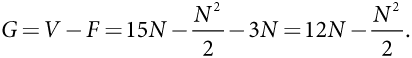
В мы вывели формулу поиска значения для максимизации функции этого вида. В частности, максимум функции
Y = A + BX − CX2
будет при X = B/(2C). В данном примере Y — это G, X — это N, A = 0, B = 12, C = 1/2. Применив формулу решения задачи максимизации, получим оптимальный выбор правительством штата значения N = 12(2 × 1/2) = 12. Следовательно, наиболее целесообразно выбрать автомагистраль на 12 полос, стоимость которой составит 36 миллиардов долларов. Таким образом, правительство предложит следующий контракт: «Мы заплатим 36 миллиардов долларов за строительство 12-полосной автомагистрали». Эта цена включает в себя нормальную прибыль, поэтому подрядчик охотно его подпишет
Аналогичным образом, если затраты составляют 5 миллиардов долларов в расчете на одну полосу, оптимальным значением N будет 10. Правительство предложит контракт на 50 миллиардов долларов за строительство 10-полосной автомагистрали. И подрядчик примет это предложение.
Б. Строительство автомагистрали: асимметричная информация
Теперь представим, что подрядчик знает, как оценить физические условия соответствующей местности, для того чтобы определить объем затрат на одну полосу автомагистрали, а правительство нет; оно может дать лишь приблизительную оценку этих затрат. Будем считать, что, по мнению правительства, объем затрат составит 3 (миллиарда долларов на одну полосу) с вероятностью 2/3 и 5 с вероятностью 1/3.
Что если правительство попытается добиться идеального оптимума и предложит подрядчику два контракта: «12-полосная автомагистраль за 36 миллиардов долларов» и «10-полосная автомагистраль за 50 миллиардов долларов»? Если объем затрат действительно составляет 3 миллиарда долларов в расчете на одну полосу, подрядчик получит больше прибыли, заключив второй контракт, хотя он и предназначен для ситуации, в которой объем затрат равен 5 миллиардов долларов на одну полосу. Истинная стоимость 10-полосной автомагистрали составит при этом 30 миллиардов долларов, и подрядчик заработает 20 миллиардов долларов сверхприбыли.
Такой исход нельзя назвать удовлетворительным. Предложенные контракты не предоставляют подрядчику достаточно сильного стимула выбирать между ними на основании объема затрат: он всегда будет отдавать предпочтение контракту на 50 миллиардов долларов. У правительства должен быть более приемлемый способ создания системы заключения контрактов на закупку.
Поэтому допустим, что правительство может разработать более общий механизм, обеспечивающий разделение типов проектов. Скажем, оно предложит подрядчику два контракта: «Контракт L: мы заплатим вам RL долларов за строительство NL полос» и «Контракт H: мы заплатим вам RH долларов за строительство NH полос». Если контракты L и H составлены правильно, при низком уровне затрат (3 миллиарда долларов на одну полосу) подрядчик выберет контракт L («low» — низкие затраты); при высоком (5 миллиардов долларов на одну полосу) — контракт H («high» — высокие затраты). Для того чтобы этот механизм скрининга работал, нужно, чтобы показатели, которые обозначены символами NL, RL, NH, RH, удовлетворяли определенным условиям.
Во-первых, по каждому контракту подрядчик, который несет соответствующие затраты (низкие при контракте L и высокие при контракте H), должен получить сумму (включающую нормальную прибыль), достаточную для покрытия его расходов. Иначе он не согласится с такими условиями и не станет заключать контракт. Следовательно, контракт должен удовлетворять двум ограничениям участия: 3NL ≤ RL для подрядчика, когда объем затрат составляет 3, и 5NH ≤ RH для подрядчика, когда объем затрат равен 5.
Кроме того, правительству необходимо составить такие два контракта, чтобы подрядчик, зная, что у него будет низкий уровень затрат, не получил выгоду, заключив контракт H и наоборот. Иначе говоря, эти контракты должны также удовлетворять двум ограничениям совместимости стимулов. Например, если истинные затраты низкие, контракт L обеспечит подрядчику сверхприбыль RL – 3NL, тогда как контракт H обеспечит сверхприбыль RH – 3NH. (Обратите внимание, что в последнем выражении количество полос и оплата те же, что и для контракта H, однако затраты подрядчика по-прежнему составляют 3, а не 5.) Для того чтобы удовлетворять ограничению совместимости при низком уровне затрат, контракты должны обеспечивать такое значение второго выражения, которое бы не превышало значение первого выражения. Следовательно, необходимо, чтобы RL – 3NL ≥ RH – 3NH. Точно так же, если истинные затраты низкие, сверхприбыль подрядчика в случае контракта L не должна превышать его сверхприбыли от контракта H. Стало быть, чтобы контракты удовлетворяли ограничению совместимости стимулов, нужно, чтобы RH – 5NH ≥ RL – 5NL.
Правительство стремится максимизировать чистую ожидаемую общественную выгоду от оплаты услуг подрядчика, поэтому использует вероятности этих двух типов в качестве весовых коэффициентов для вычисления математического ожидания. Таким образом, цель правительства — максимизировать функцию
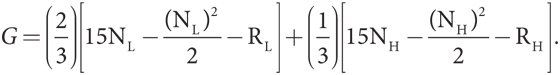
На первый взгляд может показаться, что это очень сложная задача с четырьмя переменными выбора и четырьмя ограничениями в виде неравенства. Однако ее можно существенно упростить, поскольку два ограничения являются избыточными, а оставшиеся два должны быть представлены в виде строгих равенств, что позволит нам подставить полученные выражения в уравнение вместо двух переменных.
Обратите внимание, что если ограничение участия при высоком уровне затрат 5NH ≤ RH, а ограничение совместимости стимулов при низком уровне затрат RL – 3NL ≥ RH – 3NH, выполняются оба условия; в таком случае мы можем получить следующую цепочку неравенств (где мы учитывали тот факт, что значение NH положительное):
RL – 3NL ≥ RH – 3NH ≥ 5NH – 3NH ≥ 5NH ≥ 0
Первое и последнее выражения цепочки неравенств говорят о том, что RL – 3NL ≥ 0. Поэтому нам нет необходимости отдельно рассматривать ограничение участия при низком уровне затрат 3NL ≤ RL, так как оно удовлетворяется автоматически, когда удовлетворяются два оставшихся ограничения.
Кроме того, на интуитивном уровне очевидно, что компания, которая несет большие издержки, не заинтересована заявлять о себе как о компании с низкими издержками, поскольку тогда она получит меньшую оплату при более высоких затратах. Тем не менее этот интуитивный вывод требует проверки согласно строгой логике данного анализа. В связи с этим поступим следующим образом. Сначала исключим из рассмотрения второе ограничение совместимости стимулов, RH – 5NH ≥ RL – 5NL, что позволит решить задачу с двумя оставшимися ограничениями. Затем вернемся назад и убедимся в том, что решение задачи с двумя ограничениями удовлетворяет третьему ограничению, исключенному из рассмотрения. Иначе говоря, полученное решение должно также быть решением для задачи с тремя ограничениями. (При наличии более подходящего решения оно должно быть приемлемым и для задачи с меньшим количеством ограничений.)
Таким образом, нам остается проанализировать два ограничения: 5NH ≤ RH и RL – 3NL ≥ RH – 3NH. Запишем их в таком виде: RH ≥ 5NH и RL ≥ RH + 3(NL– NH). Обратите внимание, что цель правительства — сделать значения RL и RH настолько малыми, чтобы они были совместимы с указанными выше ограничениями. Такой результат можно получить, представив каждое ограничение в виде равенства. В связи с этим примем такие равенства: RH = 5NH и RL = RH + 3(NL– NH) = 3NL + 2NH. Теперь эти выражения для платежей по контракту можно подставить в формулу целевой функции G. В результате имеем
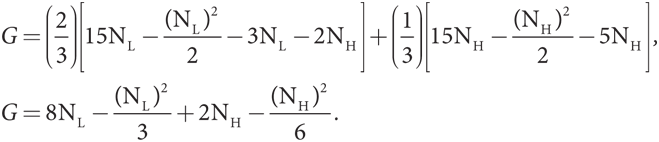
Целевая функция состоит из двух частей: одна (первые два члена) содержит только NL, а вторая (вторые два члена) только NH. Мы можем применить формулу максимизации отдельно к каждой части. В части NL A = 0, B = 8 и C = 1/3, а значит, оптимальное значение NL = 8/(2×1/3) = 24/2 = 12. В части NH A = 0, B = 2 и C = 1/6, стало быть, оптимальное значение NH = 2/(2×1/6) = 12/2 = 6.
Теперь можем использовать оптимальные значения NL и NH, чтобы получить оптимальные значения платежей (R), воспользовавшись формулами для RL и RH, выведенными выше. Подстановка в них NL = 12 и NH = 6 дает нам RH = 5 × 6 = 30 и RL = 3 × 2 + 2 × 6 = 48. Таким образом, мы имеем оптимальные значения для всех неизвестных в целевой функции правительства. Но не забывайте, что мы исключили из рассмотрения одно из ограничений совместимости стимулов, поэтому теперь нам необходимо к нему вернуться.
Мы должны убедиться, что третье ограничение, RH – 5NH ≥ RL – 5NL, согласуется с вычисленными нами значениями R и N. На самом деле так и есть. Левая сторона выражения равна 30 – 5 × 6 = 0, а правая — 48 – 5 × 12 = –12, а значит, ограничение действительно удовлетворяется.
Наше решение говорит о том, что органам власти штата нужно предложить следующих два контракта: «Контракт L: мы заплатим вам 48 миллиардов долларов за строительство 12 полос» и «Контракт H: мы заплатим вам 30 миллиардов долларов за строительство 6 полос». Как мы можем интерпретировать это решение, чтобы лучше понять его на интуитивном уровне? Интуитивное обоснование наиболее очевидно, если сравнить полученное решение с идеальным решением, найденным в при наличии полной информации о затратах. На рис. 13.2 представлены данные, позволяющие сопоставить оптимальные значения N и R.

Рис. 13.2. Значения показателей в контракте на строительство автомагистрали
Существует два важных различия между оптимальным механизмом в случае асимметричной и полной информации. Во-первых, хотя контракт, который целесообразно выбрать при условии низких затрат, подразумевает строительство такого же количества полос (12), что и при наличии полной информации, оплата по нему больше в асимметричном случае (48 вместо 36). Во-вторых, в случае асимметричной информации и высокого уровня затрат контракт подразумевает строительство меньшего количества полос (6 вместо 10), но обеспечивает такую же оплату, как и во втором варианте (30 = 6 × 5). Эти различия позволяют разделить типы.
В случае асимметричной информации у подрядчика может возникнуть соблазн сделать вид, будто он несет высокие затраты, тогда как на самом деле они низкие. Механизм оптимальной оплаты включает в себя как «пряник» для правдивого признания низких затрат, так и «кнут» за попытку симуляции высоких. «Пряник» — это сверхприбыль в размере 48 – 36 = 12, которую подрядчик заработает в результате косвенного признания низких затрат посредством выбора контракта L. «Кнут» — сокращение сверхприбыли от контракта H за счет уменьшения количества полос, которые будут при этом построены. Идеальный механизм оплаты при высоком уровне затрат подразумевает строительство 10-полосной автомагистрали за 50 миллиардов долларов; подрядчик с низким уровнем затрат заработал бы на таком контракте 50 – 3 × 10 = 20 миллиардов долларов. Оптимальный контракт с ограниченной информацией подразумевает строительство только шести полос, за что подрядчик получает 30 миллиардов долларов. Если истинный уровень затрат низкий, подрядчик заработает сверхприбыль в размере 30 – 3 × 6 = 12 миллиардов долларов. Следовательно, в этом случае он получит меньшую выгоду от завышенного уровня затрат (косвенно вытекающего из выбора подрядчиком контракта H, хотя его истинные затраты низкие). В действительности эта выгода сокращается ровно на величину, которую гарантирует часть механизма, соответствующая «прянику», что сводит на нет желание подрядчика завысить уровень издержек.
4. Фактические данные, касающиеся механизмов раскрытия информации
У рассмотренных выше механизмов есть одно общее свойство: агент владеет определенной частной информацией (в мы определили этот тип игрока). Кроме того, принципалу нужно, чтобы агент выполнил определенное действие, направленное на ее раскрытие. В терминах из эти механизмы представляют собой примеры скрининга в целях разделения типов посредством самоотбора.
Такие механизмы встречаются повсюду. Самые распространенные — механизмы ценовой дискриминации. Пока клиент готов заплатить сумму, превышающую предельные издержки компании на поставку соответствующего продукта, компания может получить прибыль за счет работы с данным клиентом. Однако его готовность платить может быть относительно низкой по сравнению с готовностью других потенциальных покупателей. Если компания должна установить одну и ту же цену всем своим клиентам, в том числе и тем, кто готов платить больше данного клиента, назначение ему цены в соответствии с его готовностью платить означает, что компании придется пожертвовать частью потенциальной прибыли от более платежеспособных клиентов. В идеале компания хотела бы прибегнуть к ценовой дискриминации, предоставив скидку клиентам с меньшей готовностью платить и не предлагая ее тем, кто готов платить больше.
Намерение компании применить ценовую дискриминацию может ограничиваться не только причинами, связанными с информацией. Такая практика может быть запрещена законом. Компания может остерегаться устанавливать высокие цены некоторым из своих клиентов из-за конкуренции со стороны других компаний. А если продукт покупает один клиент и перепродает другим, то конкуренция со стороны других покупателей может быть не менее эффективным ограничением на дискриминационное ценообразование, чем конкуренция между компаниями. Но мы сосредоточимся на информационных причинах ценовой дискриминации, оставив все остальные причины за рамками обсуждения.
По всей вероятности, в вашем местном кафе действует так называемая карта постоянного клиента: на каждых десять купленных чашек кофе вы получаете одну чашку бесплатно. Почему компания заинтересована делать это? Постоянными клиентами чаще всего становятся местные жители, у которых есть время и стимул искать самые выгодные предложения в районе. Для того чтобы переманить их от конкурентов, данному кафе необходимо предложить достаточно привлекательную цену. Напротив, случайными клиентами чаще всего бывают приезжие или люди, которые куда-то спешат и у них нет ни времени, ни стимула искать более выгодные предложения: когда у таких людей возникает потребность выпить чашку кофе и они видят кафе, они готовы заплатить любую цену (в пределах разумного, конечно). Стало быть, установление более высокой цены и выдача карты постоянного клиента позволяют кафе предоставлять скидку чувствительным к цене постоянным посетителям и не делать ее для случайных посетителей. Если у вас нет такой карты, это говорит о том, что вы относитесь ко второй категории и готовы платить больше.
Точно так же многие рестораны предлагают меню из трех блюд по фиксированной цене и недорогие комплексные блюда наряду с обычными блюдами на выбор. Такая стратегия позволяет ресторану выделить различные типы клиентов, отдающих предпочтение разным супам, салатам, основным блюдам, десертам и т. д.
Книжные издательства, как правило, сначала продают новые книги в твердых переплетах, а версию в мягкой обложке издают только через год. Зачастую разница в цене между двумя версиями гораздо больше, чем разница между себестоимостью двух видов книг. Такая схема ценообразования рассчитана на два типа покупателей: тех, кто хочет прочитать книгу как можно быстрее и готов заплатить за это больше, и тех, кто согласен ждать более выгодной цены.
Мы предлагаем вам поискать примеры подобных скрининговых механизмов ценовой дискриминации, когда будете делать покупки. Их множество. Кроме того, об этих методах есть немало интересных статей. Хороший источник информации такого рода — книга Тима Харфорда Undercover Economist.
Существует масса научных работ о механизмах закупок, которые мы представили в . В них описываются ситуации, когда покупатель взаимодействует только с одним продавцом, затраты которого относятся к категории конфиденциальной информации. Данный тип взаимодействия полностью отображает процесс разработки крупных контрактов на производство оборонительных систем вооружения или специализированного оборудования: как правило, есть только один надежный поставщик таких продуктов. Однако в реальной жизни покупатели могут делать выбор из нескольких поставщиков, при этом механизмы, создающие конкуренцию между поставщиками, приносят покупателю выгоду. Многие из этих механизмов принимают форму аукционов. Например, строительные контракты часто предоставляются подрядчику, предложившему выполнить соответствующую работу за минимальную цену (с учетом качества и сроков выполнения работы, а также других условий сделки). Примеры таких механизмов и их анализ представлены в .
5. Стимулирование усилий: простейший случай
Теперь перейдем от первого типа проблем разработки механизмов, в котором цель принципала — добиться раскрытия информации, ко второму типу, в котором присутствует моральный риск. В подобных ситуациях цель принципала — составить такой контракт, который бы стимулировал агента прилагать максимум усилий, хотя их уровень принципалом и не наблюдаем.
А. Управленческий надзор
Предположим, вы владелец компании, начинающей новый проект, и должны нанять менеджера, который будет контролировать его выполнение. Чем закончится проект — неизвестно, однако эффективный надзор может повысить вероятность успеха. Но менеджеры — обычные люди и будут пытаться прилагать как можно меньше усилий! Если эти усилия наблюдаемы, вы можете составить контракт, предусматривающий такую оплату труда менеджера, которая стимулировала бы его вкладывать достаточный объем усилий в контроль за выполнением проекта. Но если у вас нет возможности отслеживать усилия менеджера, вам необходимо заинтересовать его в успешном выполнении проекта, например, посредством выплаты премии по его завершении. Однако если приложение больших усилий не гарантирует успешной реализации проекта, то эти премии делают доход менеджера неопределенным. При этом менеджер может быть не расположен к риску, а значит, вы должны компенсировать ему возможные издержки в случае его возникновения. Вам нужно разработать такую политику оплаты труда менеджера проекта, которая бы максимизировала вашу ожидаемую прибыль с учетом того, что выбор менеджером уровня усилий зависит от характера и объема вознаграждения. Это и есть задача разработки механизма, решение которой позволит преодолеть проблемы морального риска в связи с возможным уклонением менеджера от выполнения своих обязанностей.
Рассмотрим пример с конкретными числами. Предположим, успешная реализация проекта принесет компании 1 миллион долларов прибыли сверх материальных затрат и затрат на оплату труда. В случае провала прибыль будет равна нулю. При эффективном контроле за выполнением проекта вероятность успеха равна 1/2, а при неэффективном — всего 1/4.
Как отмечалось выше, менеджер проекта не расположен к риску. В мы видели, что нерасположенность к риску можно описать с помощью вогнутой функции полезности. Возьмем в качестве примера простой случай, когда полезность u дохода y (исчисляемого в миллионах долларов) для менеджера определяется функцией квадратного корня: u = √y. Допустим, дополнительные усилия, необходимые для эффективного контроля, приносят менеджеру отрицательную полезность 0,1, и если он не будет работать на вас, он может получить другую работу, которая не требует дополнительных усилий и оплачивается в размере 90 000 долларов, или 0,09 миллиона долларов, что обеспечивает полезность √0,09 = 0,3. Таким образом, если вы хотите нанять менеджера, не требуя от него эффективного контроля, вы должны заплатить ему как минимум 90 000 долларов. Если вам необходим эффективный надзор, вы должны обеспечить менеджеру хотя бы такую же полезность, какую он мог бы получить на другой работе. Иными словами, вы должны заплатить ему сумму y, при которой √y − 0,1 не меньше 0,3, то есть √y ≥ 0,4, или y ≥ 0,16, или 160 000 долларов.
Если усилия менеджера поддаются наблюдению, вы можете заключить с ним один из двух контрактов: 1) я плачу вам 90 000 долларов, и мне все равно, насколько усердно вы будете работать; 2) я плачу вам 160 000 долларов, но вы должны проводить эффективный надзор за реализацией проекта. Выполнение второго контракта может быть обеспечено в судебном порядке, поэтому, если менеджер согласится его заключить, он не будет увиливать от работы. Ваша ожидаемая прибыль от каждого контракта зависит от вероятности успешного завершения проекта при оговоренном уровне усилий. Таким образом, в случае первого контракта ваша ожидаемая прибыль составит (1/4) × 1 – 0,09 = 0,160, или 160 000 долларов, а в случае второго (1/2) × 1 – 0,16 = 0,340, или 340 000 долларов. Следовательно, вам выгоднее заплатить менеджеру проекта за интенсивность усилий. В идеальном мире при наличии полной информации вы воспользовались бы вторым контрактом.
Теперь рассмотрим более реалистичный сценарий, когда усилия менеджера ненаблюдаемы. Эта ситуация не создает никаких дополнительных проблем, если для вас неважен уровень прилагаемых менеджером усилий и вас вполне устраивает первый контракт. Однако если этот вопрос для вас принципиален, вы должны использовать механизм стимулирования, основанный на единственном поддающемся наблюдению событии, а именно успехе или провале проекта. В связи с этим предположим, что вы предлагаете менеджеру контракт, по условиям которого он получит x в случае успешной реализации проекта и y вследствие его провала. (Обратите внимание, что x может быть равным нулю, но если это оптимальное значение, оно должно присутствовать в решении. На самом деле это значение не будет равным нулю по причине нерасположенности менеджера к риску.)
Для того чтобы побудить менеджера выбрать более высокий уровень усилий, вы должны гарантировать, что ожидаемая полезность, которую он при этом получит, превысит ожидаемую полезность в случае уклонения. При высоком уровне усилий менеджер может обеспечить успешное выполнение проекта с вероятностью 1/2, а значит, вероятность неудачи также равна 1/2. При обычном уровне усилий он может гарантировать успешную реализацию проекта только с вероятностью 1/4 (вероятность неудачи 3/4). Таким образом, ваш контракт должен обеспечивать выполнение следующего условия:
(1/2)√y + (1/2)√x − 0,1>(1/4)√y + (3/4)√x, или (1/4)(√y − √x) ≥ 0,1,
или √y − √x ≥ 0,4.
Это выражение представляет собой ограничение совместимости стимулов в данной задаче.
Далее вы должны убедиться, что менеджер получит достаточную ожидаемую полезность и будет готов работать на вас так, как вы хотите (прилагая большие усилия), вместо того чтобы принимать другое предложение. Тогда ожидаемая полезность менеджера от принятия вашего предложения о работе должна превышать полезность от альтернативной работы; таким образом, ваш контракт должен удовлетворять следующему условию:
(1/2)√y + (1/2)√x − 0,1 ≥ 0,3, или √y + √x ≥ 0,8.
Это выражение представляет собой ограничение участия в случае контракта, цель которого — добиться от менеджера повышения усилий по контролю за выполнением проекта.
С учетом этих двух ограничений необходимо максимизировать ожидаемую прибыль П. Вы рассчитываете ее, исходя из того, что выполнение указанных выше ограничений позволит вам добиться от менеджера качественной работы. В связи с этим вы надеетесь, что ваш проект будет успешно выполнен с вероятностью 1/2, а ваша ожидаемая прибыль определяется формулой
П = (1/2)(1 – у) + (1/2)(0 – х) = (1 – у – х)/2 .
Математические вычисления в этой задаче существенно упрощает использование квадратных корней x и y вместо самих x и y (другими словами, значений полезности дохода, а не показателей дохода). Запишем эти значения полезности как X = √x и Y = √y, то есть x = X2 и y = Y2. Далее необходимо максимизировать функцию П = (1 – Y2 – X2)/2 с учетом ограничения участия Y + X ≥ 0,8 и ограничения совместимости стимулов Y – X ≥ 0,4.
В формуле ожидаемой прибыли X и Y указаны со знаком минус, а значит, необходимо сделать оба значения настолько малыми, насколько допускают ограничения. В конечном счете ограничение участия выполняется в случае равенства, когда X и Y имеют малые значения. А как насчет ограничения совместимости стимулов? Если оно не выполняется в случае равенства, то оно не ограничивает выбор значений переменных и его можно исключить из рассмотрения. Предположим, именно так мы и сделали. Тогда мы можем подставить X = 0,8 – Y из ограничения участия в формулу определения прибыли и записать следующее выражение:
П = (1 – Y2 – X2)/2 = [1 – Y2 –(0,8 – Y)2]/2 = (1 – Y2 – 0,64 + 1,6Y – Y2)/2 = (0,36 + 1,6Y – 2Y2)/2 = 0,18 + 0,8Y – Y2.
Чтобы максимизировать функцию прибыли, мы снова воспользуемся формулой из . Мы имеем B = 0,8 и C = 1, что дает нам значение Y = 0,8/(2 × 1) = 0,4. Тогда X также равно X = 0,8 – 0,4 = 0,4.
Это решение подразумевает, что при исключении из рассмотрения ограничения совместимости стимулов оптимальный механизм требует равной оплаты труда менеджера как при успехе, так и при провале проекта. Такой оплаты достаточно, чтобы обеспечить менеджеру полезность 0,4 = 0,3 + 0,1 (полезность от легкой работы в другом месте плюс компенсация за отрицательную полезность дополнительных усилий в целях эффективного надзора за выполнением проекта) для выполнения ограничения участия. Этот результат подтверждается на интуитивном уровне и согласуется с анализом оптимального риска в . Менеджер не расположен, а вы нейтральны к риску (все, что вас интересует, — это ожидаемая прибыль), поэтому вам выгоднее взять весь риск на себя и исключить элемент случайности из дохода менеджера.
Но если менеджер получает один и тот же доход независимо от того, как завершится проект, у него нет стимула прилагать ненаблюдаемые усилия. При этом не принятое во внимание ограничение совместимости стимулов не будет выполняться автоматически, и нам необходимо убедиться в том, что X и Y действительно удовлетворяют ему. Следовательно, оба ограничения должны выполняться в случае равенств Y + X = 0,8 и Y – X = 0,4. Объединив их, получим 2Y = 1,2, или Y = 0,6; этот результат сразу же дает нам X = 0,2. В переводе с полезности на денежные суммы имеем x = X2 = 0,04 и y = Y2 = 0,36. Таким образом, менеджеру нужно заплатить 40 000 долларов, если проект завершится провалом, и 360 000 долларов — если успехом. Это меньше оговоренных в контракте 1 (подразумевающем низкий уровень усилий) 90 000 долларов в случае провала и больше оговоренных в контракте 2 (высокий уровень усилий в ситуации с полной информацией) 160 000 долларов в случае успеха. Это означает, что менеджера ожидает сочетание «кнута» (низкая оплата в случае провала проекта) и «пряника» (высокая оплата в случае успеха проекта), как это было с подрядчиком в примере со строительством автомагистрали в .
При такой схеме вы (владелец) получите ожидаемую прибыль П = (1 – 0,36 – 0,04)/2 = 0,03, или 300 000 долларов. Эта сумма меньше 340 000 долларов, которые вы бы заработали в идеальной ситуации с полной информацией, когда могли бы составить поддающийся принудительному исполнению контракт, требующий высокого уровня усилий. Разница в размере 40 000 долларов — неизбежные издержки в связи с асимметричностью информации.
Схему оплаты труда менеджера можно описать так: базовая заработная плата в размере 40 000 долларов и премия за успешное выполнение проекта в сумме 320 000 долларов, или (что то же самое) 40 000 заработной платы и доля 32% в операционной прибыли в размере 1 миллион долларов. Нецелесообразно полагаться только на участие в прибылях, не предложив менеджеру базовую зарплату. Почему? Если бы базовая зарплата равнялась нулю, то в случае успешного выполнения проекта вам пришлось бы выплатить менеджеру сумму y, которая определяется формулой (1/2)√y − 0,1 = 0,3 или y = 0,64, или 640 000 долларов, чтобы обеспечить его участие. Ваша ожидаемая прибыль составила бы при этом: П = (1 – 0,64 – 0)/2 = 0,18, или 180 000 долларов, что на 120 000 долларов ниже, чем если бы вы предложили базовую ставку зарплаты и премию (а также на целых 160 000 долларов меньше, чем в ситуации с полной информацией).
Такое снижение прибыли обусловлено нерасположенностью менеджера к риску. Премиальная система оплаты делает его доход весьма рискованным, поэтому, чтобы обеспечить его участие в проекте, вам необходимо назначить настолько большую премию, что это сократит вашу прибыль. Оптимальная система оплаты в условиях асимметричной информации создает приемлемый баланс между «кнутом» и «пряником», обеспечивая менеджеру достаточный стимул для повышения усилий по надзору за выполнением проекта, но не подвергая при этом его доход существенному риску.
Б. Страхование
Помимо описанных выше ситуаций на рынке труда, моральный риск может возникать и в ходе других взаимодействий. В частности, ему подвержены рынки страховых услуг. Страховым компаниям необходимо решить, как составить приемлемые договоры страхования, стимулирующие клиентов предпринимать действия, снижающие вероятность подачи ими иска о страховом возмещении. Например, страховые компании хотели бы, чтобы люди, которым они продают полисы медицинского страхования, регулярно проходили профилактические медицинские осмотры, а люди, которым они продают полисы автострахования, продолжали практиковать безопасный стиль вождения. Но поскольку у страховой компании, как правило, нет возможности наблюдать за действиями клиентов, создание подходящего страхового полиса требует понимания теории разработки механизмов в условиях асимметричной информации.
Вернемся к примеру с фермером из , который сталкивается с риском потери урожая из-за плохих погодных условий, таких как засуха. Тогда мы выдвинули предположение, что его доход составит 160 000 долларов при благоприятной погоде и 40 000 при неблагоприятной. Когда эти два сценария в равной степени вероятны (вероятность 0,5 в каждом случае), ожидаемый доход фермера составляет 0,5 × 160 000 + 0,5 × 40 000 = 100 000 долларов. Однако при этом среднем значении фермер сталкивается со значительным риском, и если он к нему не склонен, то его будет больше интересовать ожидаемая полезность полученных результатов, а не просто ожидаемый доход.
Предположим, фермер действительно не расположен к риску. В его ситуации функция полезности имеет вид u = √I, где I — доход фермера. Следовательно, фермер получает полезность 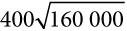 , если погода хорошая (дожди), и полезность
, если погода хорошая (дожди), и полезность 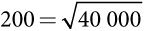 , если погода плохая (засуха). Тогда его ожидаемая полезность равна 0,5 × 400 + 0,5 × 200 = 300.
, если погода плохая (засуха). Тогда его ожидаемая полезность равна 0,5 × 400 + 0,5 × 200 = 300.
Что произойдет, если фермеру удастся избежать риска, связанного с угрозой засухи? В частности, в какой ситуации он окажется при наличии возможности всегда получать 100 000 долларов (в данном примере это ожидаемая стоимость), а не 160 000 долларов в одной половине случаев и 40 000 долларов во второй? Давайте на какое-то время оставим в стороне вопрос о том, как фермер мог бы этого добиться, и обратим внимание на то, что при таком исходе он ежегодно получал бы полезность около 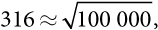 то есть у фермера была бы более высокая ожидаемая полезность (316 > 300), если бы он нашел способ получать одинаковый доход (а также полезность) в годы с благоприятными и неблагоприятными погодными условиями.
то есть у фермера была бы более высокая ожидаемая полезность (316 > 300), если бы он нашел способ получать одинаковый доход (а также полезность) в годы с благоприятными и неблагоприятными погодными условиями.
Один из возможных способов добиться выравнивания доходов — страхование. Нейтральная по отношению к риску страховая компания могла бы предложить фермеру контракт, по условиям которого фермер выплачивает компании 60 000 долларов в годы с благоприятными погодными условиями, а страховщик выплачивает фермеру 60 000 долларов в годы с неблагоприятными погодными условиями. Поскольку вероятность каждого исхода — 50%, ожидаемая прибыль страховой компании при этом равна нулю, что просто обеспечивает ее готовность предложить фермеру такой контракт. С другой стороны, его заключение принесло бы фермеру явную выгоду, так как его ожидаемая полезность возрастает. Следовательно, для обеих сторон был бы приемлем договор страхования, который является полным (покрывает все издержки в связи с неблагоприятным исходом) и справедливым (цена полиса страхования достаточна для возмещения страховых претензий фермера).
До сих пор в этом примере не было проблем с информацией. Однако фермер может предпринимать различные действия, чтобы уменьшить вероятность низкого уровня дохода по причине засухи. Например, он может построить водосборный резервуар, чтобы поливать свои поля в самые засушливые годы. Но строительство и текущий ремонт резервуара требуют определенных затрат. Если фермер построит качественный резервуар и будет за ним следить, то это позволит ему защитить себя от связанных с засухой рисков. Но если резервуар будет протекать, а фермер не будет проводить текущий ремонт, то такой резервуар не выполнит свою функцию, а значит, не снизит риск потери урожая. Если фермер хорошо застрахован, а проверить качество водосборного резервуара и его текущего ремонта посредством обычного осмотра нельзя, у фермера может возникнуть желание уклониться от выполнения этой задачи, чтобы не нести соответствующих затрат. Вероятность такого уклонения и есть источник морального риска в нашем примере.
Предположим, отрицательная полезность в связи с дополнительными затратами на строительство и уход за качественным водосборным резервуаром составляет 25; при этом фермер сокращает вероятность неблагоприятного исхода на 25%. Тогда при наличии водосборного резервуара ожидаемый доход фермера равен 0,75 × 160 000 + 0,25 × 40 000 = 130 000 долларов, а его ожидаемая полезность (при отсутствии страхования) — 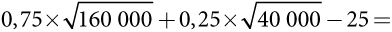 0,75 × 400 + 0,25 × 200 – 25 = 350 – 25 = 325. То есть при наличии водосборного резервуара ожидаемая полезность выше, чем без него (325 > 300), поэтому если страхование недоступно, фермеру целесообразно предпринять усилия по снижению риска, например, построив водосборный резервуар.
0,75 × 400 + 0,25 × 200 – 25 = 350 – 25 = 325. То есть при наличии водосборного резервуара ожидаемая полезность выше, чем без него (325 > 300), поэтому если страхование недоступно, фермеру целесообразно предпринять усилия по снижению риска, например, построив водосборный резервуар.
Однако фермер все же может извлечь для себя выгоду из страхования. Страховой полис с выравниванием доходов, который гарантирует фермеру 130 000 долларов каждый год, обеспечил бы ему ожидаемую полезность в размере 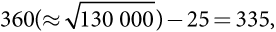 даже когда он построит качественный водосборный резервуар и будет проводить его текущий ремонт. Эта полезность выше полезности 325, которую фермер получает, если строит резервуар, но не имеет страховки, поэтому фермер непременно воспользуется страхованием.
даже когда он построит качественный водосборный резервуар и будет проводить его текущий ремонт. Эта полезность выше полезности 325, которую фермер получает, если строит резервуар, но не имеет страховки, поэтому фермер непременно воспользуется страхованием.
Предположим, существует возможность составить полный и справедливый договор страхования, в котором сказано, что фермер должен принять меры по снижению вероятности неблагоприятного исхода на 25%. Допустим также, что страховая компания может это проконтролировать, направив к фермеру страхового агента для проверки состояния водосборного резервуара. В таком случае, согласно условиям договора страхования, обеспечивающего ежегодный доход 130 000, фермер должен выплачивать страховой компании 30 000 за год с благоприятными погодными условиями, а страховщик фермеру — 90 000 долларов за год с неблагоприятными. Как и прежде, ожидаемая прибыль страховой компании равна нулю (0,75 × 30 000 – 0,25 × 90 000 = 0), но ожидаемая полезность для фермера увеличивается (до 335), поэтому обе стороны примут условия контракта.
Но ситуация меняется, если страховщик не имеет возможности проконтролировать фермера. Фермер может пойти на обман и согласиться на договор страхования «вы платите 30 000 в благоприятный год и получаете 90 000 долларов в неблагоприятный год», но при этом ничего не предпринимать для снижения риска (то есть построить некачественный водосборный резервуар и не проводить его технического обслуживания). Тогда вероятность неблагоприятного года возвращается к 50%, а доход фермера ежегодно составляет 130 000 долларов. Ожидаемая полезность, которую получит фермер, заключив такой контракт, но не выполняя его условий, равна 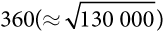 — то есть больше, чем во всех предыдущих случаях. Безусловно, эта ситуация невыгодна страховой компании, поскольку ее ожидаемая прибыль составит 0,5 × 30 000 – 0,5 × 90 000 = –30 000 долларов. Стало быть, условия контракта неприемлемы для страховщика, поэтому он не станет предлагать его фермеру.
— то есть больше, чем во всех предыдущих случаях. Безусловно, эта ситуация невыгодна страховой компании, поскольку ее ожидаемая прибыль составит 0,5 × 30 000 – 0,5 × 90 000 = –30 000 долларов. Стало быть, условия контракта неприемлемы для страховщика, поэтому он не станет предлагать его фермеру.
Означает ли это, что фермер вообще не сможет оформить договор страхования, если построит водосборный резервуар и обеспечит его текущий ремонт, а страховщик не сможет это контролировать? Нет. Однако это означает, что фермер не может получить полное страхование, но у него есть вариант заключить договор частичного страхования, по условиям которого страховая компания берет на себя только часть риска, связанного с неблагоприятным исходом.
Напомним, что если фермер построит качественный резервуар и будет правильно за ним ухаживать, согласно полному страхованию он должен выплачивать страховщику 30 000 долларов за благоприятный год и получать от него 90 000 долларов за неблагоприятный год. В действительности такой контракт не стимулирует фермера строить или содержать водосборный резервуар, поэтому страховщик получает отрицательную ожидаемую прибыль. Для того чтобы разработать в данной ситуации оптимальную схему страхования, страховой компании необходимо определить правильное значение суммы X, которую она должна получить в качестве платежа от фермера за благоприятный год (что оставит фермеру 160 000 – X долларов), и правильное значение суммы Y, которую компания должна выплатить фермеру за неблагоприятный год (что увеличит его доход до 40 000 + Y долларов). В таком случае оптимальный механизм страхования должен максимизировать ожидаемую прибыль страховой компании с учетом значений X, Y и вероятностей различных исходов и в то же время гарантировать как сохранение заинтересованности фермера в строительстве водосборного резервуара, так и его готовность заключить договор страхования.
Поскольку процесс вычисления значений X и Y довольно сложный, мы вместо этого рассмотрим конкретную пару чисел, при которых фермер получит частичное страхование и стимулы принять меры, направленные на снижение риска, а компания сможет выйти на уровень безубыточности. Предположим, страховая компания предлагает фермеру договор, предусматривающий страхование рисков в объеме, равном третьей части полного страхования. По условиям контракта, платеж фермера должен составлять 10 000 долларов за благоприятный год (при этом у него останется 150 000 дохода), а выплата фермеру — 30 000 за неблагоприятный год (что обеспечит ему 70 000 долларов). Если фермер все же построит качественный водосборный резервуар и будет регулярно проводить его техническое обслуживание, то контракт обеспечит страховой компании ожидаемую прибыль 0,75 × 10 000 – 0,25 × 30 000 = 7500 – 7500 = 0, а значит, компания захочет предложить фермеру страхование на этом уровне.
Но станет ли фермер соблюдать условия контракта? Другими словами, обеспечивает ли контракт совместимость стимулов? Да, если ожидаемая полезность для фермера при условии страхования и выполнения оговоренных условий превышает ожидаемую полезность заключения договора страхования без выполнения оговоренных мер. То есть такой контракт должен удовлетворять следующему неравенству:
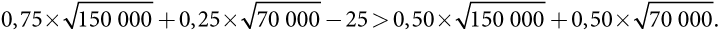
Вычисление значений этих двух выражений дает (приблизительно) 331 > 326, неравенство верно. Следовательно, данный договор частичного страхования удовлетворяет ограничению совместимости стимулов, а значит, побуждает фермера прилагать усилия, направленные на снижение вероятности неблагоприятного исхода.
Удовлетворяет ли этот контракт ограничению участия? Да. Он должен обеспечить фермеру минимум такую же ожидаемую полезность, как он бы получил без страхования. Как мы рассчитали выше, она равна 325, а в результате заключения договора составит 331. Следовательно, фермеру выгоднее заключить договор частичного страхования, чем вообще остаться без страховки, поэтому обе стороны согласятся с его условиями.
Фактические данные, подтверждающие эту теорию страхования и морального риска, можно найти в любом договоре страхования. Большинство страховых полисов содержат различные требования о собственном удержании страхователя и участии в оплате, оставляя часть риска держателя полиса незастрахованным в целях снижения морального риска.
6. Стимулирование усилий: фактические данные и дополнительные возможности
Система стимулирования усилий менеджера проекта, о которой шла речь в , представляла собой компромисс между созданием для него более мощного стимула к повышению усилий и требованием взять на себя больше риска ответственности за обеспечение прибыли компании. Этот компромисс очень важен на практике, но его необходимо рассматривать в сочетании с другими элементами взаимоотношений компании и работника, большинство из которых связаны со многими аспектами протекающих в компании процессов. Качество и количество усилий не просто вопрос хорошего или плохого отношения к работе, а полученные результаты — не просто вопрос успеха или неудачи; в каждом из этих случаев присутствует широкий диапазон возможностей, а такие элементы, как время работы и прибыль, могут непрерывно меняться. В компании работает много сотрудников, и общий итог ее деятельности зависит от их действий. У большинства компаний широкий ассортимент продукции, а каждый работник выполняет много разных задач. Кроме того, взаимодействие между организацией и ее сотрудниками долгосрочное, а не на время одного проекта или короткого периода. Соответственно, все эти элементы требуют более сложных систем стимулирования. В данном разделе мы кратко проанализируем некоторые из них и предоставим ссылки на большое количество источников для более глубокого изучения данной темы. В основе систем стимулирования лежат сложные математические расчеты, поэтому мы просто объясним их на интуитивном уровне, а строгий формальный анализ оставим для более углубленных курсов.
А. Нелинейные системы стимулирования
Может ли оптимальная система стимулирования усилий менеджера всегда определяться базовой заработной платой и участием в прибылях? Нет. При наличии трех возможных исходов (провал проекта, умеренный успех и большой успех) выраженная в процентах премия за переход от провала к умеренному успеху может не совпадать с премией за переход от умеренного к большому успеху. Следовательно, оптимальная система стимулирования может быть нелинейной.
Давайте немного изменим пример с надзором за выполнением проекта из , включив в него три возможных исхода: прибыль за вычетом материальных затрат и затрат на оплату труда 0 долларов, 500 000 долларов и 1 миллион долларов. Предположим также, что высокий уровень усилий по контролю за выполнением проекта обеспечивает вероятность успеха 1/6, 1/3 и 1/2 по трем возможным исходам в том же порядке. Низкий уровень усилий по надзору обеспечивает обратную последовательность вероятностей успеха — 1/2, 1/3 и 1/6 соответственно. Тогда несколько более сложные вычисления (которые мы оставляем в качестве дополнительного упражнения) показывают, что оптимальная оплата труда менеджера проекта равна 30 625 долларов в случае неудачи проекта, 160 000 долларов при умеренном успехе и 225 625 долларов при наилучшем исходе. Если в этой системе оплаты представить сумму 30 625 долларов как базовую заработную плату, то премия за успешное выполнение проекта составит 129 375 долларов за обеспечение прибыли 500 000 долларов и 195 000 за обеспечение прибыли 1 миллион долларов. Премия представляет собой долю в прибыли в размере 26% за первый уровень успеха и всего 13% за второй уровень.
На практике используются особые формы нелинейных систем стимулирования. Самая распространенная подразумевает выплату заранее оговоренной фиксированной премии в случае достижения определенного уровня эффективности или нормы выработки. Когда целесообразно применять такую систему?
Схема выплаты премии за выполнение нормы выработки представляет собой мощный стимул, если эта норма установлена на таком уровне, что повышение усилий работника существенно увеличивает вероятность ее выполнения. В качестве иллюстрации рассмотрим пример, когда компания хочет, чтобы каждый агент по продажам обеспечивал объем продаж в размере 1 миллион долларов, и готова платить за это до 100 000 долларов. Если компания выплачивает агенту по продажам фиксированные комиссионные в размере 10%, его дополнительные усилия по увеличению объема продаж с 900 000 долларов до 1 миллиона долларов принесут ему 10 000 долларов. Но если компания предложит агенту по продажам заработную плату 60 000 долларов и премию 40 000 долларов за выполнение нормы продаж в размере 1 миллион долларов, то дополнительные усилия агента на последнем этапе позволят ему выполнить норму и заработать еще 40 000 долларов. Таким образом, установление нормы продаж предоставляет торговцу гораздо более сильный стимул приложить дополнительные усилия.
Однако такая система стимулирования не лишена недостатков. Норму выработки необходимо определить достаточно точно. Предположим, компания допускает ошибку в расчетах и устанавливает норму продаж на уровне 1,2 миллиона долларов, при этом агент по продажам понимает, что вероятность ее выполнения крайне мала, даже если он приложит сверхчеловеческие усилия. В итоге он просто откажется от дальнейших попыток, не станет напрягаться и обеспечит объем продаж даже меньше 1 миллиона долларов. Более того, чистая система стимулирования «норма — премия» не дает ему никаких стимулов превысить уровень в 1 миллион долларов. И наконец, норма рассчитана на определенный период, как правило, календарный год, а это порождает еще более порочные системы стимулирования. Агент по продажам, которому просто не везет в течение первых нескольких месяцев, придет к выводу, что у него уже нет шанса выполнить годовую норму, поэтому он может расслабиться и не прилагать особых усилий до конца года. В свою очередь агент, которому сопутствует удача, уже в июле выполнит норму продаж, и у него тоже не будет стимула усердствовать до конца года, так что он может даже попытаться манипулировать такой системой стимулирования, договорившись с некоторыми клиентами отложить выполнение их заказов до следующего года, чтобы повысить свои шансы на выполнение нормы продаж в следующем году. Линейная система стимулирования наподобие описанной выше системы с участием в прибылях менее подвержена таким манипуляциям.
Поэтому компании обычно используют сочетание нормы выработки и более дифференцированной, состоящей из отдельных фрагментов, линейной системы оплаты. Например, агент по продажам может получать базовую заработную плату, низкие комиссионные за объем продаж от 500 000 до 1 миллиона долларов, более высокую ставку комиссионного вознаграждения за объем продаж от 1 до 2 миллионов долларов и т. д.
Управляющие взаимных фондов часто получают вознаграждение за высокую эффективность на протяжении календарного года. Оно выплачивается за счет компании в виде премий, а также за счет инвесторов, вкладывающих деньги в соответствующий фонд. Если эти схемы вознаграждения нелинейные, управляющие реагируют изменением профиля риска инвестиционного портфеля своего фонда. В мы видели, что человек с вогнутой функцией полезности не расположен к риску, а человек с выпуклой функцией полезности склонен рисковать. Подобно тому как любители риска предпочитают рискованные ситуации безопасным, управляющий, столкнувшийся с выпуклой функцией полезности, повысит уровень риска инвестиционного портфеля своего фонда.
Б. Стимулирование в командах
Сотрудники компании редко занимаются выполнением тех или иных задач в одиночку. Агенты по продажам, отвечающие за определенные регионы, наиболее близки к такой модели, но даже их эффективность зависит от поддержки сотрудников главного офиса компании. Как правило, люди работают в командах, и результат работы всей команды определяют усилия каждого ее члена. Например, прибыль компании в целом зависит от эффективности работы всего персонала. Такая зависимость создает особые проблемы в плане разработки системы стимулирования.
Когда заработок одного работника зависит от прибыли всей компании, каждый отдельно взятый сотрудник видит только слабую связь между своими усилиями и совокупной прибылью, при этом каждый получает в ней лишь небольшую долю. А эта доля — весьма слабый стимул прилагать повышенные усилия к выполнению своих обязанностей. Даже в небольших командах у каждого члена может возникнуть соблазн увильнуть от работы и воспользоваться плодами труда своих коллег. (Как в дилемме заключенных с коллективным действием в контексте игры «уличный сад», о которой шла речь в , и , помните?) Если команда невелика и работает в одном составе на протяжении достаточно продолжительного периода, можно ожидать, что ее члены решат дилемму, разработав внутреннюю и, возможно, не денежную схему вознаграждений и наказаний наподобие той, о которой говорилось в .
В другом контексте наличие в одной команде большого количества работников может усилить стимулы. Допустим, в компании многие работники выполняют аналогичные задачи, например продают отдельные продукты из ее продуктовой линейки. Если в продажах каждого работника присутствует общий (положительно коррелированный) случайный элемент, который может зависеть от состояния реальной экономики, то объем продаж одного работника относительно объема продаж другого работника — хороший показатель их относительных уровней усилий. Например, усилия работников 1 и 2, обозначенные как x1 и x2, могут быть связаны с их продажами y1 = x1 + r и y2 = x2 + r, где r — общая случайная погрешность в объеме продаж (или общий «фактор удачи»). Из этого следует, что разности y2 – y1 = x2 – x1 будут уже без всякой случайности; иными словами, разность между фактическими объемами продаж в точности эквивалентна разности между уровнем усилий, прилагаемых работниками 1 и 2.
Работодатель может вознаграждать этих работников в соответствии с относительными результатами каждого из них. Такая система оплаты не содержит для работников никакого риска. Упомянутый в компромисс между обеспечением оптимального уровня усилий и участием в прибылях в этой системе отсутствует. Если у первого работника низкий объем продаж и он объясняет это невезением, компания может возразить: «Тогда почему второй работник добился весомых результатов? Вы же оба находились в одинаковых условиях, значит, вы, наверное, прилагали меньше усилий». Безусловно, если эти работники могут вступить в сговор, это поставит под угрозу цель компании, но если этого не произойдет, компания может внедрить эффективную систему стимулирования, заставив работников конкурировать друг с другом. Показательный пример такой системы — состязание, в котором приз получает тот, кто демонстрирует более высокие результаты.
Соревнования позволяют смягчить еще одну потенциальную проблему морального риска. В реальной жизни критерии успеха не так уж легко поддаются наблюдению. Поэтому у владельца компании может возникнуть искушение заявить, что никто из работников не проявил особого рвения и никто не заслуживает премии. Состязание с призом, который необходимо кому-то вручить, или заранее выделенный совокупный премиальный фонд, подлежащий распределению среди работников, устраняет этот моральный риск, возникающий по вине принципала.
В. Множественные задачи и результаты
Работники обычно выполняют несколько задач для своих работодателей, что приводит к получению ряда наблюдаемых исходов усилий работника. При этом между стимулированием усилий по выполнению различных задач возникает зависимость, усложняющая разработку механизма стимулирования.
Исход каждой задачи агента отчасти зависит от его усилий и отчасти от случая. Именно поэтому схема стимулирования, основанная на полученных результатах, зачастую подвергает риску выигрыш агента. Если элемент случайности незначителен, риск агента низкий, а значит, стимул прилагать усилия можно повысить. Безусловно, результаты выполнения различных задач зависят от случая в разной степени. Следовательно, если принципал будет разрабатывать систему стимулирования, отдельно анализируя каждую задачу, он использует более сильные стимулы для усилий по выполнению задач с меньшим элементом случайности и более слабые для усилий по выполнению задач, результат которых является более неопределенным показателем усилий агента. Однако мощный стимул для одной задачи отвлечет усилия агента от другой, что еще больше снизит эффективность ее выполнения. Для того чтобы предотвратить такое перераспределение усилий, принципал должен ослабить стимул и в случае этой задачи.
Подобные примеры нередки в нашей жизни. В обязанности профессора входит как научно-исследовательская работа, так и преподавание. Существует много точных показателей эффективных научных исследований: публикации научных работ, назначения на должности редакторов престижных журналов, избрание в академию наук и т. д. Напротив, результаты преподавательской работы в меньшей степени наблюдаемы, а если это и происходит, то с большим запаздыванием. Студентам, как правило, необходимо накопить многолетний опыт, прежде чем они поймут ценность того, чему научились в университете; в краткосрочной перспективе на них скорее произведет впечатление умение преподавателя показать себя, а не передать свои знания. Если бы эти две задачи, стоящие перед преподавателями, рассматривались по отдельности, администраторы университета привязали бы более сильные стимулы к научным исследованиям, а более слабые — к преподаванию. Однако тогда профессора перенаправили бы усилия с преподавания на научную работу (даже в большей степени, чем они уже это делают в некоторых вузах). В связи с этим отсутствие возможности точно отследить результаты преподавания вынуждает деканов факультетов и ректоров университетов предлагать слабые стимулы за научные исследования.
Самый известный пример ситуации с множественными задачами и результатами касается школьного обучения. Некоторые результаты преподавания, такие как баллы за тесты, поддаются точному наблюдению, тогда как другие значимые аспекты образования, например способность работать в команде или умение выступать на публике, измеримы в меньшей степени. Если вознаграждение учителей зависит от баллов, полученных их учениками за тесты, они будут готовить к ним учеников, а другие аспекты обучения игнорировать. Такое «обыгрывание» системы стимулирования распространяется и на спорт. Если в бейсболе хиттер получает вознаграждение только за выбитые хоум-раны, он будет пренебрегать другими аспектами отбивания (принятие подач, выполнение сэкрифайс-бантов и пр.), хотя порой они могли бы повысить шансы его команды на победу. Точно так же агент по продажам может пожертвовать долгосрочными отношениями с клиентом ради достижения краткосрочных целей по обеспечению продаж.
Если проблема деструктивного влияния некоторых стимулов на другие задачи становится слишком серьезной, могут понадобиться другие системы вознаграждения за выполнение задач. В таком случае может быть использован более целостный, хотя и более субъективный критерий эффективности работы, такой как общая оценка со стороны руководителя: работники могут направить свои усилия на те виды деятельности, которые одобрил босс!
Г. Стимулирование в долгосрочной перспективе
Как правило, трудовые отношения поддерживаются на протяжении длительного времени, что позволяет компаниям создавать системы стимулирования, основанные на концепции отложенного вознаграждения, то есть эффективность вашей работы вознаграждается впоследствии. Компании регулярно используют продвижение по службе, оплату по стажу и прочие формы отсроченного вознаграждения. По сути, труд работников на начальных этапах карьеры компания оплачивает по заниженной ставке, а затем ставка поднимается. Перспектива будущего вознаграждения мотивирует более молодых работников прилагать больше усилий к выполнению своих обязанностей, а также побуждает их оставаться в компании, что снижает текучесть кадров. Безусловно, у компании может возникнуть соблазн отказаться от своего неявного обещания о более высокой оплате в последующие годы, поэтому эффективность таких систем зависит от их достоверности. Чаще всего они наиболее действенны в компаниях, имеющих долгую историю стабильности и известных хорошим отношением к работникам старшего возраста.
Еще один способ обеспечить мотивацию работников посредством перспективы будущего вознаграждения — использование так называемой эффективной заработной платы. Компания платит работнику заработную плату, превышающую общепринятый уровень, а разница между двумя ставками представляет собой излишек, или экономическую ренту работника. Работник получает ее при условии добросовестного выполнения обязанностей, но если он начнет филонить, это может быть обнаружено и его уволят. В итоге ему придется вернуться на общий рынок труда, где он сможет получать только общепринятую заработную плату.
Компания сталкивается с задачей разработки механизма при попытке определить приемлемый уровень эффективной заработной платы. Предположим, общепринятая ставка заработной платы составляет w0, а эффективная заработная плата компании равна w > w0. Пусть денежный эквивалент субъективных издержек в связи с приложением надлежащих усилий равен e. На протяжении каждого периода оплаты работник может выбирать, насколько интенсивно трудиться. Если он решит не прилагать особых усилий, это позволит ему сэкономить e, однако с вероятностью p такое увиливание от работы будет обнаружено. Тогда работник потеряет излишек (w – w0) начиная со следующего периода оплаты, и это будет продолжаться неопределенное время. Пусть r — процентная ставка между двумя периодами. Если работник уклоняется от работы сегодня, ожидаемая приведенная стоимость его убытков за следующий период составит p (w – w0)/(1 + r). Кроме того, работник будет терять w – w0 с вероятностью p на протяжении всех последующих периодов оплаты. Вычисления, аналогичные сделанным для повторяющихся игр в и в , показывают, что общая ожидаемая приведенная стоимость будущих убытков работника равна
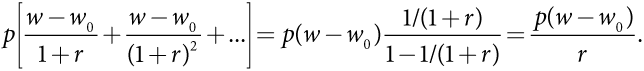
Для того чтобы у работника не возникало желания уклоняться от выполнения своих обязанностей, компании необходимо сделать так, чтобы его ожидаемый убыток был не меньше прямой выгоды от увиливания от работы, e. Следовательно, компания должна платить работнику эффективную заработную плату, удовлетворяющую следующему условию:
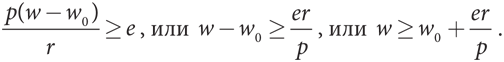
Следовательно, при минимальной эффективной заработной плате это выражение превращается в равенство. Чем точнее компания сумеет определить факт уклонения от работы (то есть чем выше значение p), тем меньше может быть превышение эффективной заработной платы над общепринятой ставкой.
Кроме того, повторяющееся взаимодействие позволяет компании разработать и более эффективную систему стимулирования. Как мы уже говорили, результаты труда работника за любой отдельно взятый период представляют собой сочетание приложенных им усилий и элемента случайности. Однако если эти результаты оставляют желать лучшего год за годом, работник не может постоянно списывать это на счет невезения. Стало быть, согласно закону больших чисел, средний результат за длительный период можно использовать в качестве более точного показателя среднего уровня прилагаемых работником усилий и исходя из этого вознаградить работника или наказать.
Резюме
Изучение процесса разработки механизмов можно кратко описать как анализ ситуации «как иметь дело с тем, кто знает больше вас». Такие ситуации возникают во множестве контекстов, как правило, в ходе взаимодействия между более информированным игроком, то есть агентом, и менее информированным, то есть принципалом, который стремится разработать механизм, позволяющий ему привести стимулы агента в соответствие со своей целью.
Существует два типа проблем, связанных с разработкой механизмов. Первый касается раскрытия информации, когда принципал создает систему скрининга информации, имеющейся в распоряжении агента. Второй относится к моральному риску, когда принципал создает систему, позволяющую добиться от агента оптимального уровня наблюдаемых действий. В обоих случаях принципал пытается максимизировать свою целевую функцию с учетом таких ограничений агента, как ограничение совместимости стимулов и ограничение участия.
Компании используют механизмы раскрытия информации при создании систем ценообразования, позволяющих разделить клиентов на типы по их готовности платить за продукцию компании. Контракты на закупки также помогают разделить проекты (или подрядчиков) на типы в соответствии с уровнем затрат. На реальных рынках можно найти конкретные примеры как ценовой дискриминации, так и скрининга посредством закупочных контрактов.
При наличии морального риска работодатели должны составлять контракты таким образом, чтобы побуждать работников к приложению оптимальных усилий. Аналогичным образом страховые компании составляют полисы страхования, стимулирующие клиентов принимать меры по предотвращению страховых случаев. В некоторых простых ситуациях в качестве оптимальных контрактов могут выступать линейные схемы, тогда как при более сложном взаимодействии часто выгоднее нелинейные схемы. Системы стимулирования, предназначенные для членов команд или рассчитанные на длительное взаимодействие, как правило, сложнее, чем разработанные для более простых ситуаций.
Ключевые термины
Агент
Принципал
Проблема (взаимоотношение) «принципал–агент»
Разработка механизма
Ценовая дискриминация
Упражнения с решениями
S1. Компании, предоставляющие клиентам страховую защиту на случай убытков в связи с грабежом или аварией, вне всяких сомнений, заинтересованы в надлежащем поведении держателей страховых полисов. Предложите несколько идей для разработки системы стимулирования, которую могла бы использовать страховая компания для предотвращения и обнаружения мошенничества или неосторожного поведения со стороны держателей полисов.
S2. Некоторые компании продают свои продукты либо по отдельности, либо в наборах, чтобы увеличить прибыль посредством разделения клиентов с разным предпочтениями.
a) Приведите три примера оптовых скидок в зависимости от количества купленного товара, предлагаемых компаниями.
b) Как такие скидки позволяют компаниям выполнить скрининг клиентов для выяснения их предпочтений?
S3. Компания Omniscient Wireless Limited (OWL) планирует развернуть новую национальную беспроводную телефонную сеть широкополосного доступа в следующем месяце. OWL провела маркетинговое исследование, по результатам которого было установлено, что 10 миллионов ее потенциальных клиентов разделены на два сегмента, которые в компании назвали так: «нерегулярные пользователи» и «регулярные пользователи». Среди первых более низкий спрос на услуги беспроводной телефонной связи, в частности они вряд ли смогут создать для компании ценность, превышающую 300 минут звонков в месяц. Вторые испытывают более высокую потребность в услугах беспроводной телефонной связи и могут создать для компании ценность, превышающую 300 минут звонков в месяц. Аналитики OWL определили, что лучше всего предложить клиентам такие тарифные планы: 300 минут и 600 минут в месяц соответственно. По их оценкам, 50% клиентов относятся к сегменту нерегулярных пользователей и 50% — к сегменту регулярных пользователей, причем каждому типу свойственна следующая готовность платить за каждый тип услуг:

Затратами OWL на одну дополнительную минуту беспроводной связи можно пренебречь, поэтому абонплата составляет 10 долларов в месяц на одного пользователя, какой бы тарифный план он ни выбрал.
Каждый потенциальный клиент вычисляет чистый выигрыш (выгода минус цена), который он получит от каждого тарифного плана, и выбирает план, обеспечивающий более высокий чистый выигрыш, если он не является отрицательным. Если оба плана обеспечивают клиенту эквивалентные неотрицательные чистые выигрыши, он выбирает 600 минут; если оба плана приносят клиенту отрицательные чистые выигрыши, он не покупает ни один из них. Компании OWL необходимо максимизировать свою ожидаемую прибыль на одного потенциального клиента.
a) Предположим, компания предлагает пользователям тарифный план на 300, а не на 600 минут. Какую оптимальную цену следует назначить, и какую среднюю прибыль на одного потенциального клиента получит при этом OWL?
b) Допустим, компания предлагает пользователям тарифный план на 600 минут. Какую оптимальную цену следует назначить, и какую среднюю прибыль на одного потенциального клиента получит при этом OWL?
c) Предположим, компания решила предложить оба тарифных плана, причем ей выгодно, чтобы нерегулярные пользователи покупали тарифный план 300 минут, а регулярные пользователи — 600 минут. Составьте ограничение совместимости стимулов для нерегулярного пользователя.
d) Аналогичным образом составьте ограничение совместимости стимулов для регулярного пользователя.
e) Используя результаты, полученные в пунктах c и d, вычислите оптимальные цены на тарифные планы 300 и 600 минут, чтобы каждый пользователь покупал предназначенный для него тарифный план. Какой будет прибыль компании на одного потенциального клиента?
f) Проанализируйте исходы, описанные в пунктах а, b и e. В каждой из трех ситуаций определите, является ли соответствующий исход разделяющим, объединяющим или полуразделяющим.
S4. Mictel Corporation обладает мировой монополией на производство персональных компьютеров. Компания может выпускать компьютеры двух типов: с низкой производительностью и с высокой производительностью. Пятая часть потенциальных покупателей пользуются компьютерами только время от времени, тогда как остальные постоянно.
Затраты на производство двух типов ПК, а также выгода, которую они приносят двум типам потенциальных покупателей, представлены в следующей таблице (все данные отображены в тысячах долларов):
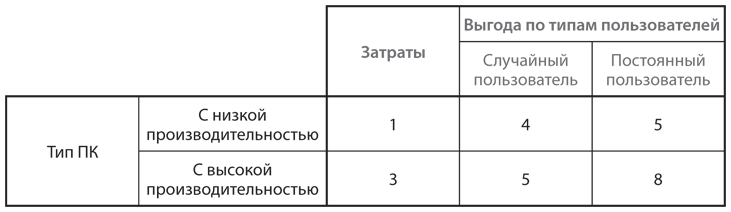
Каждый тип покупателей рассчитывает свой чистый выигрыш (выгода минус цена), который он получил бы в случае покупки компьютера каждого типа, и покупает ПК, обеспечивающий более высокий чистый выигрыш, если он не отрицательный. Если оба типа компьютеров обеспечивают эквивалентные неотрицательные выигрыши, покупатель выбирает высокопроизводительный компьютер; если оба типа приносят отрицательные чистые выигрыши, он вообще ничего не покупает. Компании Mictel необходимо максимизировать свою ожидаемую прибыль.
a) Если бы Mictel располагала всей полнотой информации, то, зная тип потенциального клиента, она могла бы предлагать ему только один вид компьютера по установленной цене, придерживаясь принципа «хотите берите, хотите нет». Какой компьютер и по какой цене компания предложила бы каждому типу покупателей?
На самом деле компании Mictel неизвестен тип каждого отдельно взятого покупателя, поэтому она составляет каталог, из которого все покупатели могут выбирать компьютеры.
b) Сначала предположим, что компания выпускает только компьютеры с низкой производительностью и продает их по цене x. Какое значение x обеспечит Mictel максимальную прибыль? Почему?
c) Теперь допустим, что компания выпускает только компьютеры с высокой производительностью и продает их по цене y. Какое значение y обеспечит Mictel максимальную прибыль? Почему?
d) И наконец, предположим, что компания выпускает оба типа компьютеров, продавая ПК с низкой производительностью по цене x, а с высокой по цене y. Каким ограничениям совместимости стимулов должна удовлетворять компания по значениям x и y, если она хочет, чтобы случайные пользователи покупали компьютеры с низкой производительностью, а постоянные — с высокой производительностью?
e) Каким ограничениям участия должны удовлетворять значения x и y для того, чтобы случайные пользователи были готовы покупать компьютеры с низкой производительностью, а постоянные — компьютеры с высокой производительностью?
f) С учетом ограничений, найденных в пунктах d и e, какие значения x и y максимизируют ожидаемую прибыль компании, когда она продает оба типа ПК? Какова ожидаемая прибыль Mictel вследствие такой политики?
g) С учетом всех сделанных выше выводов определите, какой политики в области производства и ценообразования должна придерживаться компания.
S5. Еще раз выполните исходя из предположения, что половина клиентов компании Mictel — случайные пользователи.
S6. На основании выводов, полученных в и , решите для общего случая, в котором доля случайных пользователей составляет c, а доля постоянных пользователей — (1 – c). Ответы на некоторые части этих упражнений зависят от значения c. В этих случаях перечислите все возможные варианты и объясните, как они зависят от значения c.
S7. Дисконтный кинотеатр Sticky Shoe продает попкорн и газированную воду в специальных торговых точках. Кэмерон, Джесси и Шон — постоянные клиенты Sticky Shoe; каждый из них оценивает попкорн и газированную воду следующим образом:

Кроме этой троицы, в кинотеатр Sticky Shoe ходят еще 2997 жителей Харкинсвилля, одна треть которых оценивают попкорн и газированную воду так же, как Кэмерон, еще одна треть — как Джессика, и еще треть — как Шон. Если клиенту безразлично, покупать попкорн и напитки или нет, он покупает. Приготовление дополнительной порции попкорна или напитка Sticky Shoe не стоит практически ничего.
a) Если Sticky Shoe устанавливает отдельные цены на попкорн и напитки, какой должна быть цена каждого продукта, чтобы максимизировать прибыль? Какую прибыль получит Sticky Shoe, продавая попкорн и газированную воду отдельно?
b) Что будет покупать каждый тип клиентов (Кэмерон, Джессика и Шон), если Sticky Shoe установит отдельные цены на попкорн и газированную воду, обеспечивающие максимальную прибыль?
c) Вместо продажи продуктов по отдельности Sticky Shoe решает продавать их вместе, назначая одну цену на весь набор. Какая единая цена за набор обеспечит Sticky Shoe максимальную прибыль? Какую прибыль получит Sticky Shoe, продавая попкорн и газированную воду только вместе?
d) Что будет покупать каждый тип клиентов, если Sticky Shoe установит единую цену на попкорн и газированную воду в одном наборе, обеспечивающую максимальную прибыль? Чем этот ответ отличается от ответа в пункте b?
e) Какой схеме ценообразования отдает предпочтение каждый тип клиентов? Почему?
f) Если бы кинотеатр Sticky Shoe продавал попкорн и газированную воду как в наборах, так и отдельно, какие продукты (попкорн, газированную воду или их набор) он захотел бы продавать каждому типу клиентов? Как Sticky Shoe может добиться, чтобы каждый клиент покупал продукт, предназначенный именно для него?
g) Какие цены (на попкорн, газированную воду и набор из этих продуктов) установил бы Sticky Shoe, чтобы максимизировать свою прибыль? Какую прибыль получит Sticky Shoe, продавая продукты по этим трем ценам?
h) Чем отличаются ответы в пунктах а, c и g? Объясните причины.
S8. В данной главы рассказывается о проблеме «принципал–агент» в контексте компании, которая решает, как стимулировать менеджера проекта прилагать больше усилий к повышению вероятности его успешной реализации. Стоимость успешного проекта составляет 1 миллион долларов; вероятность успеха при высоком уровне усилий равна 0,5; при низком — 0,25. Полезность дохода для менеджера равна квадратному корню из суммы вознаграждения (исчисляемого в миллионах долларов), а отрицательная полезность приложения больших усилий составляет 0,1. Однако минимальная заработная плата менеджера равна теперь 160 000 долларов.
a) Какой контракт предложит компания менеджеру проекта, если ее устраивает его низкий уровень усилий?
b) Какова ожидаемая прибыль компании в случае, если ее система стимулирования обеспечивает низкий уровень усилий менеджера проекта?
c) Какую пару контрактов (y, x), где y — заработная плата в случае успешного выполнения проекта, а x — заработная плата в случае провала проекта, компания должна предложить менеджеру, чтобы он был заинтересован повысить уровень усилий?
d) Какова ожидаемая прибыль компании при обеспечении высокого уровня усилий?
e) Какого уровня усилий компания ждет от менеджера? Почему?
S9. Компания застраховала свое основное производственное предприятие от пожара. Вероятность пожара на предприятии без программы противопожарных мероприятий равна 0,01, а при наличии такой программы 0,001. В случае пожара размер убытков составит 300 000 долларов. Выполнение программы противопожарных мероприятий обошлось бы в 80 долларов, но страховая компания не может без дополнительных затрат отслеживать ход выполнения противопожарных мероприятий.
a) Почему в этой ситуации возникает моральный риск? Каков его источник?
b) Может ли страховая компания устранить проблему морального риска? Если да, то как? Если нет, объясните почему.
S10. В 1781 году Моцарт переехал из Зальцбурга в Вену, надеясь получить место при дворе Габсбургов. Но вместо того чтобы просить его, Моцарт решил ждать, когда император призовет его к себе сам, поскольку «если кто-то делает шаг первым, он получает меньшую оплату». Проанализируйте эту ситуацию с точки зрения теории игр с асимметричной информацией, в том числе принципов сигнализирования и скрининга.
S11 (дополнительное упражнение, требующее исчисления). Вы министр Океании по вопросам мира, и ваша работа — закупать военное имущество для своей страны. Исчисляемая в долларах Океании чистая выгода от объема Q этого имущества равна 2Q1/2 – M, где M — сумма денег, выплаченных за имущество.
Есть только один поставщик военного имущества — Baron Myerson’s Armaments (BMA). Вы не знаете, какие производственные затраты он несет. Общеизвестно, что затраты BMA на производство единицы продукции — это постоянная величина, равная 0,10 с вероятностью p = 0,4 и 0,16 с вероятностью 1 – p. Назовем BMA компанией с низким уровнем затрат, если ее производственные затраты не превышают 0,10, и компанией с высоким уровнем затрат, если ее затраты составляют 0,16. Истинный тип затрат известен только самой BMA.
В прошлом ваше министерство использовало два типа контрактов на закупку: «затраты плюс» и контракт с фиксированной ценой. Но контракты «затраты плюс» создают для BMA стимул завышать свой уровень затрат, а в случае контрактов с фиксированной ценой компании может быть заплачено больше, чем необходимо. Вы принимаете решение предложить BMA на выбор два возможных контракта:
Контракт 1: мы выплатим вам сумму M1 за поставку количества Q1.
Контракт 2: мы выплатим вам сумму M2 за поставку количества Q2.
Необходимо выбрать такие значения Q1, M1, Q2 и M2, чтобы для компании BMA с низким уровнем затрат более выгодным был контракт 1, а для компании BMA с высоким уровнем затрат — контракт 2. Если другой контракт обеспечивает аналогичную прибыль, то BMA с низким уровнем затрат выберет контракт 1, а BMA с высоким уровнем затрат — контракт 2. Кроме того, независимо от уровня затрат, компании BMA нужно получить как минимум нулевую экономическую прибыль в случае любого выбранного контракта.
a) Составьте формулы для определения прибыли BMA с низким уровнем затрат и BMA с высоким уровнем затрат в случае, когда компания получает сумму M за поставку количества Q.
b) Выведите формулы ограничения совместимости стимулов, побуждающих BMA с низким уровнем затрат выбрать контракт 1, а BMA с высоким уровнем затрат — контракт 2.
c) Сформулируйте ограничения участия для каждого типа BMA.
d) Выведите формулу определения ожидаемой чистой выгоды Океании в случае, если компания BMA каждого типа выберет контракт, ориентированный именно на этот тип.
Теперь ваша задача — выбрать значения Q1, M1, Q2 и M2, обеспечивающие максимальную ожидаемую чистую выгоду, вычисленную в пункте d, с учетом ограничения совместимости стимулов (incentive-compatibility, IC) и ограничения участия (participation constraint, PC)
e) Допустим, Q1 > Q2, а также предположим, что ограничения IC1 и PC2 связывающие, то есть выполняются в случае равенства, а не в случае слабого неравенства. Используйте их для определения нижних пределов значений M1 и M2, достижимых при соответствующих значениях Q1 и Q2.
f) Докажите, что в случае связывающих ограничений IC1 и PC2 ограничения IC2 и PC1 удовлетворяются автоматически.
g) Подставьте выражения, полученные в пункте c, вместо M1 и M2, чтобы выразить целевую функцию через Q1 и Q2.
h) Запишите условия максимизации первого порядка и решите их относительно Q1 и Q2.
i) Найдите решение относительно M1 и M2.
j) Какую ожидаемую чистую выгоду получит Океания, предложив такой выбор контрактов?
k) Какие общие принципы скрининга проиллюстрированы в этом списке контрактов?
S12 (дополнительное упражнение). Вернитесь к задаче из и проанализируйте, чем оптимальный список найденных в ней контрактов отличается от некоторых альтернативных контрактов.
a) Если бы вы решили предложить один контракт с фиксированной ценой, ориентированный на привлечение только BMA с низким уровнем затрат, каким бы он был? Другими словами, какая пара (Q, M) была бы оптимальной, если бы вы знали, что BMA — компания с низким уровнем затрат?
b) Приняла бы компания BMA с высоким уровнем затрат контракт, предложенный в пункте а? Почему да или почему нет?
c) Какой была бы ожидаемая чистая выгода Океании от предложения контракта из пункта а с учетом вероятности того, что BMA — это компания с низким уровнем затрат? Как этот показатель отличается от ожидаемой чистой выгоды в случае списка контрактов, составленного в ?
d) Какой контракт с фиксированной ценой вы бы предложили BMA с высоким уровнем затрат?
e) Компания BMA с низким уровнем затрат согласилась бы принять контракт, составленный в пункте d? Какой была бы ее прибыль в случае согласия?
f) С учетом вашего ответа в пункте e какой была бы ожидаемая чистая выгода Океании, если бы она предложила контракт из пункта d? Как этот показатель отличается от ожидаемой чистой выгоды в случае списка контрактов, составленного в ?
g) Рассмотрите случай, когда сотрудник BMA, занимающийся промышленным шпионажем, пообещал сообщить вам точный объем затрат на единицу продукции, что позволит Океании предложить только один контракт с фиксированной ценой, рассчитанный на истинный тип компании BMA. Какой была бы ожидаемая чистая выгода Океании, если бы ей было известно, что она получит информацию об истинном типе BMA? Как это соотносится с пунктами c и f данного упражнения, а также с ?
Упражнения без решений
U1. Какие проблемы морального риска и (или) неблагоприятного отбора могут возникнуть в следующих ситуациях? В каждом случае кратко опишите некоторые системы стимулирования и (или) стратегии сигнализирования и скрининга, направленные на преодоление этих проблем. От вас не требуется никаких математических вычислений, но вы должны дать четкое экономическое обоснование того, почему и как работают предложенные вами методы.
a) Ваш финансовый консультант говорит вам, какие акции покупать или продавать.
b) Вы обращаетесь к риелтору, решив продать свой дом.
c) Вы посещаете своего врача либо для проведения планового медицинского осмотра, либо для лечения.
U2. MicroStuff — компания по выпуску программного обеспечения, которая продает два популярных приложения WordStuff и ExcelStuff. Выпуск дополнительной копии программ не требует от MicroStuff никаких затрат. У MicroStuff есть три типа потенциальных клиентов, которых представляют Ингрид, Хавьера и Кэти. В общем существует 100 миллионов потенциальных клиентов каждого типа, для которых каждое приложение представляет такую ценность в долларах:
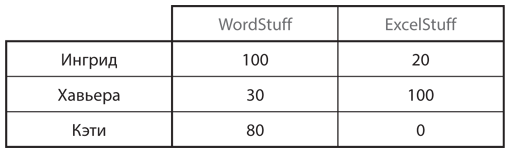
a) Если компания MicroStuff устанавливает отдельные цены на приложения WordStuff и ExcelStuff, какой должна быть цена каждого из них, обеспечивающая компании максимальную прибыль?
b) Что предпочтет каждый тип клиентов (Ингрид, Хавьера и Кэти), если MicroStuff установит отдельные цены на WordStuff и ExcelStuff, обеспечивающие максимальную прибыль?
c) Вместо продажи приложений WordStuff и ExcelStuff по отдельности MicroStuff решает продавать их вместе, назначая одну цену на весь комплект. Какая единая цена за пакет обеспечит MicroStuff максимальную прибыль? Какую прибыль получит MicroStuff, продавая WordStuff и ExcelStuff только в комплекте?
d) Что будет покупать каждый тип клиентов (Ингрид, Хавьера и Кэти), если MicroStuff установит единую цену на комплект приложений WordStuff и ExcelStuff, обеспечивающую максимальную прибыль? Чем этот ответ отличается от ответа в пункте b?
e) Какой схеме ценообразования отдает предпочтение каждый тип клиентов? Почему?
f) Если бы компания MicroStuff продавала приложения WordStuff и ExcelStuff как в комплекте, так и отдельно, какие продукты (WordStuff, ExcelStuff или пакет приложений) она захотела бы продавать каждому типу клиентов? Как MicroStuff может добиться того, чтобы каждый клиент покупал продукт, предназначенный именно для него?
g) Какие цены на WordStuff, ExcelStuff или пакет приложений установила бы компания MicroStuff, чтобы максимизировать свою прибыль? Какую прибыль получит MicroStuff, продавая свои продукты по этим трем ценам?
h) Чем отличаются ответы в пунктах а, c и g? Объясните причины.
U3. Рассмотрите пример с уровнем усилий менеджера проекта, аналогичный примеру из . Стоимость успешного проекта составляет 420 000 долларов; вероятность успеха равна 1/2 при наличии эффективного контроля за выполнением проекта и 1/4 без него. Менеджер нейтрален к риску, а не избегает его, как в , поэтому его ожидаемая полезность равна ожидаемой прибыли за вычетом отрицательной полезности усилий. Он может получить работу в другом месте с оплатой 90 000 долларов; при этом отрицательная полезность дополнительных усилий, которые ему придется прилагать к выполнению вашего проекта, составляет 100 000 долларов.
a) Продемонстрируйте, что стимулирование высокого уровня усилий потребует от компании предложить менеджеру систему вознаграждения с отрицательной базовой ставкой заработной платы; другими словами, если проект потерпит неудачу, менеджер должен выплатить компании оговоренную в контракте сумму.
b) Как можно реализовать на практике идею отрицательной базовой ставки заработной платы?
c) Докажите, что если отрицательную базовую ставку заработной платы установить невозможно, то компании выгоднее пойти на низкую оплату труда менеджера при низком уровне усилий с его стороны.
U4. Cheapskates — профессиональная хоккейная команда низшей лиги. Спорткомплекс команды может вместить всех 1000 болельщиков, которые захотят посмотреть ее домашние матчи, и может предложить два типа мест: обычные и эксклюзивные. Есть также два типа болельщиков: 60 процентов — болельщики из числа «синих воротничков», а остальные — «белые воротнички». Данные о затратах на предоставление мест каждого типа, а также о готовности болельщиков за них платить приведены в следующей таблице (в долларах):

Каждый болельщик купит максимум одно место, в зависимости от излишка потребителя (максимальная готовность платить минус фактическая цена). Если этот излишек в обоих случаях отрицательный, то болельщик вообще не станет покупать билет. Если хотя бы один тип мест обеспечивает болельщику неотрицательный излишек, то он купит место того типа, который предоставляет более высокий излишек. Если оба типа мест гарантируют эквивалентные неотрицательные излишки, тогда «синий воротничок» выберет обычное место, а «белый» — эксклюзивное.
Владельцы команды предоставляют разные места и определяют на них цены таким образом, чтобы максимизировать свою прибыль. Они устанавливают цены на каждый тип мест, продают по ним как можно больше билетов, а затем предоставляют информацию о количестве и типах мест каждого вида, на которые были проданы билеты.
a) Сперва предположим, что владельцы команды могут определить тип каждого отдельно взятого болельщика, который приходит к окошку билетной кассы (скажем, по типу воротничка), и могут предложить ему соответствующий тип места по установленной цене, придерживаясь принципа «хотите берите, хотите нет». Какой была бы максимальная прибыль владельцев команды π* при такой системе?
b) Теперь допустим, что владельцы команды не имеют возможности определить тип каждого отдельно взятого болельщика, но им известна доля «синих воротничков». Пусть цена обычного места равна X, а цена эксклюзивного — Y. При каких ограничениях совместимости стимулов «синие воротнички» будут покупать обычные места, а «белые» — эксклюзивные? Постройте график этих ограничений на плоскости с осями X и Y.
c) Какие ограничения участия определяют решения болельщиков о покупке билетов? Отобразите эти ограничения на графике, построенном в пункте b.
d) Какие цены X и Y с учетом ограничений, найденных в пунктах b и c, обеспечат владельцам команды максимальную прибыль π2 при такой системе ценообразования? Чему равно значение π2?
e) Владельцы команды подумывают установить цены на таком уровне, чтобы билеты покупали только «белые воротнички». Какой будет прибыль владельцев πw, если они решат обслуживать только эту категорию болельщиков?
f) Сравнив значения π2 и πw, определите политику ценообразования, которую выберут владельцы команды. Как прибыль, полученная ими вследствие такой политики, отличается от прибыли π* при наличии полной информации?
g) Чему равны затраты на преодоление асимметричности информации в пункте f? Кто несет на себе эти затраты? Почему?
U5. Выполните , исходя из предположения, что 10% болельщиков относятся к числу «синих воротничков».
U6. На основании выводов, полученных в и , решите для общего случая, в котором доля «синих воротничков» составляет B, а доля «белых воротничков» — (1 – B). Ответы на некоторые части упражнения зависят от значения B. В этих случаях перечислите все возможные варианты и объясните, как они зависят от значения B.
U7. Во многих ситуациях агенты прилагают большие усилия к тому, чтобы получить более высокооплачиваемую должность, при этом оплата труда фиксированная и агенты конкурируют между собой за эти должности. Теория состязаний рассматривает группу агентов, конкурирующих за фиксированную совокупность призов. В этом случае все, что нужно для победы, — это позиции одного агента относительно другого, а не абсолютный уровень эффективности.
a) Сформулируйте причины, по которым компания может прибегнуть к описанной выше состязательной системе. Проанализируйте ее влияние на стимулы компании и ее работников.
b) Сформулируйте причины, по которым компания может отказаться от использования описанной выше состязательной системы.
c) Приведите один конкретный прогноз теории состязаний, а также пример эмпирических данных, поддерживающих этот прогноз.
U8. Выполните со следующими изменениями: из-за ухода некоторых самых талантливых инженеров вероятность успеха при высоком уровне усилий по надзору составляет всего 0,4, а вероятность успеха при низком уровне усилий снижается до 0,24.
U9 (дополнительное упражнение). Преподаватель хочет определить, насколько его студенты уверены в своих способностях, и предлагает следующую схему: «После того как ответите на вопрос, укажите свою оценку вероятности того, что вы правы. Затем я проверю ваш ответ на вопрос. Предположим, вы оценили вероятность как x. Если ваш ответ действительно правильный, вы получите оценку log(x), если неправильный — log(1 – x)». Продемонстрируйте, что такая схема будет стимулировать студентов давать правдивую оценку; иными словами, покажите, что если вероятность правильного ответа равна p, то приведенная студентами оценка x = p.
U10 (дополнительное упражнение). Выполните , исходя из предположения о том, что BMA — компания с низким уровнем затрат с вероятностью 0,6.
U11 (дополнительное упражнение). Выполните , исходя из предположения, что в компании BMA с низким уровнем издержек затраты на единицу продукции составляют 0,2 с вероятностью 0,38. Пусть вероятность того, что BMA — это компания с низким уровнем затрат, составляет 0,4.
U12 (дополнительное упражнение). Вернитесь к истории с Океанией, где она закупает военное имущество у BMA (см. ). Теперь проанализируйте ситуацию, в которой в BMA есть три возможных типа затрат: c1, c2 и c3, где c3 > c2 > c1. BMA несет затраты c1 с вероятностью p1, затраты c2 с вероятностью p2 и затраты c3 с вероятностью p3, где p1 + p2 + p3 = 1. Далее будем говорить, что компания BMA принадлежит к типу i, если ее затраты составляют ci при i = 1, 2, 3.
Вы предлагаете выбор из трех возможностей: «Мы выплатим вам сумму Mi за поставку количества Qi при i = 1, 2, 3». Предположим, выбор более одного контракта обеспечивает равную прибыль, поэтому BMA типа i выберет контракт i. Для того чтобы удовлетворять условию участия, контракт i должен гарантировать компании BMA типа i неотрицательную прибыль.
a) Выведите формулу определения прибыли BMA типа i в случае, когда компания получает сумму M за поставку количества Q.
b) Сформулируйте условия ограничения участия для каждого типа BMA.
c) Укажите шесть ограничений совместимости стимулов. Другими словами, составьте выражение для каждого типа i, согласно которому прибыль, которую получит BMA в случае выбора контракта i, будет больше или равна прибыли, которую она получит при выборе двух других контрактов.
d) Составьте формулу определения ожидаемой чистой выгоды Океании B. Это и есть целевая функция (функция, которую необходимо максимизировать).
Теперь ваша задача — выбрать три значения Qi и три значения Mi, обеспечивающие максимальную ожидаемую чистую выгоду с учетом ограничения совместимости стимулов (IC) и ограничения участия (PC).
e) Начните с трех ограничений: ограничение IC в отношении типа 2 подразумевает, что компания предпочтет контракт 2 контракту 3; ограничение IC в отношении типа 1 подразумевает, что компания предпочитает контракт 1 контракту 2; а также ограничение участия в отношении типа 3. Предположим, Q1 > Q2> Q3. Используйте эти ограничения для определения нижних пределов значений М1, М2 и М3, достижимых при соответствующих значениях c1, c2 и c3, а также Q1, Q2 и Q3. (Обратите внимание, что в выражении для нижней границы по каждому значению M может присутствовать два или более значения c и Q.)
f) Докажите, что три ограничения (два IC и одно PC), о которых идет речь в пункте е, связывающие в точке оптимума.
g) Теперь докажите, что, если три ограничения в пункте f связывающие, еще шесть ограничений (оставшиеся ограничения IC и два ограничения PC) удовлетворяются автоматически.
h) Подставьте соответствующие выражения вместо Мi, выразив целевую функцию только через три Qi.
i) Запишите условия максимизации первого порядка и решите их относительно Qi. То есть возьмите три частные производные ∂Qi/∂B, приравняйте их к нулю и решите это уравнение относительно Qi.
j) Докажите, что указанное условие Q1 > Q2 > Q3 будет выполнено в точке оптимума, если