11 Коллективные игры
В играх и стратегических ситуациях, рассмотренных в предыдущих главах, как правило, участвовало всего два или три игрока, поддерживающих взаимодействие. Такие игры распространены в нашей академической, деловой, политической и личной жизни, а значит, их очень важно осмыслить и проанализировать. Тем не менее немало случаев социального, экономического и политического взаимодействия представляют собой стратегические ситуации с одновременным участием множества игроков. Стратегии построения карьеры, инвестиционные планы, маршруты передвижения на работу и обратно в часы пик и даже обучение — все это сопряжено с преимуществами и издержками, зависящими от действий многих людей. Если вы были в одной из этих ситуаций, то, скорее всего, ловили себя на мысли, что что-то здесь не так: например, слишком много студентов, инвесторов и пассажиров толпились именно там, куда нужно было и вам. Или наоборот: желающих поучаствовать в каком-либо благотворительном проекте оказывалось слишком мало, хотя вы и прилагали максимум усилий, чтобы их привлечь. Иными словами, игры со многими участниками, которые ведутся в обществе, часто приводят к результату, не удовлетворяющему большинство, а то и всех его членов. В данной главе мы рассмотрим такие игры с точки зрения уже разработанной нами теории. Это поможет вам понять, что именно в подобных играх идет не так и как с этим бороться.
В самом общем виде игры с участием множества игроков касаются проблем коллективного действия. Лучший способ достижения целей общества в целом или отдельного коллектива — выполнение их членами определенного действия или действий, хотя эти действия не всегда отвечают интересам отдельных людей. Иными словами, наиболее благоприятный для общества исход не обеспечивается автоматически в виде равновесия Нэша. Поэтому мы должны определить, как игра может быть изменена, чтобы она приводила к оптимальному исходу или как минимум улучшала неудовлетворительный исход в случае равновесия Нэша. Но для этого сперва следует понять природу таких игр. Их три типа, и вы с ними уже знакомы: дилемма заключенных, игра в труса и игра в доверие. Несмотря на то что в этой главе основное внимание уделяется играм с одновременным участием множества игроков, мы начнем с уже хорошо знакомых вам игр между двумя участниками.
1. Коллективные игры с двумя участниками
Представьте, что вы фермер и для вас и соседнего фермера несомненную пользу принесет строительство системы орошения и противопаводковой защиты. Вы можете объединить усилия по реализации этого проекта с соседом или сделать все самостоятельно. Однако после завершения строительства другой фермер автоматически извлечет из него выгоду. Другими словами, каждый из вас заинтересован переложить всю работу на другого. В этом и состоит суть вашего стратегического взаимодействия и проблема коллективного действия.
В мы уже встречались с подобной игрой, когда каждая из трех соседок принимала решение об инвестициях в уличный сад, которым бы наслаждались все трое. Эта игра стала дилеммой заключенных, и все три ее участницы попытались уклониться от решения вносить вклад; в данной главе анализируется более общий диапазон возможных вариантов структуры выигрышей. Кроме того, в игре «уличный сад» мы оценивали ее исходы по шкале от 1 до 6; в процессе описания общих игр мы рассмотрим и более общие формы преимуществ и издержек в случае каждого игрока.
Наш ирригационный проект имеет две важные характеристики. Во-первых, его преимущества относятся к категории неисключаемых благ: человеку, который не внес вклад в его реализацию, нельзя помешать извлекать из него выгоду. Во-вторых, к категории неконкурентных благ: использование этих преимуществ одним человеком не мешает другому тоже ими пользоваться. Экономисты называют эти проекты чистым общественным благом; в качестве примера такого блага часто приводится национальная система обороны. Напротив, чистое частное благо — полностью исключаемое и конкурентное: тот, кто не платит за него, не может воспользоваться его преимуществами, а если такое благо получает один человек, больше к нему никто не имеет доступа. Буханка хлеба — хороший пример чистого частного блага. Большинство благ попадают в двумерный диапазон различных степеней исключаемости и конкурентности. Мы не будем углубляться в эту классификацию, но упомянули о ней, чтобы помочь вам соотнести наше обсуждение с тем, что вы можете встретить в других курсах и книгах.
А. Коллективное действие в контексте дилеммы заключенных
Издержки и преимущества, связанные со строительством оросительной системы, так же как издержки и преимущества всех коллективных действий, зависят от того, кто принимает участие в проекте. В свою очередь, относительный объем затрат и выгод определяет структуру игры, которая при этом ведется. Предположим, каждый из вас в одиночку мог бы завершить проект за 7 недель, тогда как при объединении усилий это потребовало бы от каждого всего по 4 недели. Кроме того, качество проекта с участием двух человек выше; от его реализации в одиночку фермер получает выгоду, эквивалентную 6 неделям работы, тогда как совместная реализация обеспечивает каждому выгоду, эквивалентную 8 неделям работы.
В более общем плане мы можем выразить преимущества и издержки в виде функций от количества участников игры. Таким образом, ваши издержки в связи с решением строить оросительную систему зависят от того, будете вы это делать в одиночку или с чьей-то помощью. Стало быть, издержки можно записать как C(n), где C зависит от количества игроков n, участвующих в реализации проекта. Тогда C(1) — это ваши расходы в связи со строительством оросительной системы только своими силами, C(2) — вместе с соседом. В данном примере C(1) = 7, а C(2) = 4. Аналогичным образом выгода (B) от готовой оросительной системы может зависеть от числа участников (n) ее строительства. В нашем примере B(1) = 6, а B(2) = 8. Обратите внимание, что, учитывая характер проекта, обеспечивающего создание социального блага, преимущества каждого фермера одинаковы, независимо от степени участия в его реализации.
В данной игре каждый фермер должен решить, участвовать ему в строительстве оросительной системы или нет, то есть попытаться уклониться. (Предполагается, что работу необходимо выполнить в сжатые сроки, и вы могли бы сделать вид, что вас в последнюю минуту отвлекли какие-то важные семейные дела; так же может поступить и ваш сосед.) На рис. 11.1 представлена таблица выигрышей в этой игре, исчисляемых в неделях работы. Значения выигрышей определены на основании разности между издержками и преимуществами, связанными с каждым действием. Таким образом, выигрыш при выборе стратегии «строить» составит B(n) – C(n) при n = 1, если вы реализуете проект в одиночку, и n = 2, если ваш сосед также выберет «строить». Выигрыш от применения стратегии «не строить» равен просто B(1), если ваш сосед сыграет «строить», поскольку в случае отказа от участия в проекте вы не несете никаких издержек.
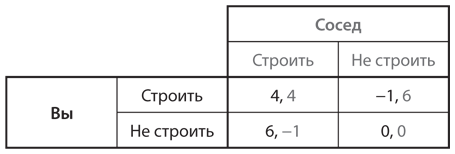
Рис. 11.1. Коллективное действие в контексте дилеммы заключенных: версия I
Учитывая структуру выигрышей, представленную на рис. 11.1, ваш наилучший ответ в случае, если сосед откажется участвовать в проекте, — также отказаться: ваш выигрыш от реализации проекта в одиночку (6) меньше понесенных вами издержек (7), то есть ваш чистый выигрыш составит −1, тогда как отказ от участия в проекте обеспечит выигрыш 0. Аналогичным образом, если ваш сосед решит участвовать в проекте, вы сможете извлечь для себя выгоду (6) из его работы без всяких затрат со своей стороны; для вас это лучше, чем работать самому, чтобы получить более крупное преимущество от проекта с участием двух человек (8), но при этом понести издержки в связи с выполнением работы (4), что обеспечивает чистый выигрыш 4. Общее свойство этой игры состоит в том, что для вас лучше не участвовать в строительстве оросительной системы, что бы ни сделал ваш сосед; та же логика справедлива и в его случае. (В данном примере каждый фермер выступает в качестве безбилетника — человека, который перекладывает всю работу на соседа, а затем все равно пожинает ее плоды.) Таким образом, «не строить» — доминирующая стратегия каждого игрока. Однако совместная работа над проектом принесла бы обоим фермерам больше пользы (выигрыш 4), чем в случае отказа от его реализации (выигрыш 0). Следовательно, это игра категории «дилемма заключенных».
В ней мы видим одну из основных проблем, возникающих в играх с коллективным действием. Выбор, оптимальный для каждого игрока в отдельности (в данном случае — не принимать участия в строительстве независимо от решения соседа), может не быть оптимальным с точки зрения всей группы, даже если эта группа состоит из двух фермеров. Социальный оптимум в игре с коллективным действием достигается, если общая сумма выигрышей ее участников максимизируется. В данной дилемме заключенных социальный оптимум сводится к исходу «строить» / «строить». Однако поведение игроков в соответствии с равновесием Нэша не всегда обеспечивает социально оптимальный исход. Именно поэтому изучение игр с коллективным действием сфокусировано на методах улучшения наблюдаемого (как правило, соответствующего равновесию Нэша) поведения в целях обеспечения наиболее благоприятных для всего общества исходов. Как мы увидим, противоречие между такими исходами, как равновесие Нэша и социальный оптимум, присутствует во всех версиях игр с коллективным действием.
Теперь давайте проанализируем, как будет выглядеть эта игра, если слегка изменить показатели. Предположим, что выгоды от проекта с участием двух человек ненамного превышают выгоды от проекта с участием одного человека: 6,3 недели работы для каждого фермера. При этом каждый получит 6,3 – 4 = 2,3, если оба решат строить. Полученные в итоге выигрыши представлены в таблице на рис. 11.2. Эта игра по-прежнему остается дилеммой заключенных и приводит к равновесному исходу «не строить» / «не строить». Тем не менее, если оба фермера решают строить, их общий выигрыш составит всего 4,6. Социальный оптимум наблюдается в случае, когда один из них принимает участие в строительстве, а другой нет, что обеспечивает обоим выигрыш 6 + (–1) = 5. Есть два возможных способа получить такой исход, но тогда достижение социального оптимума поднимает новую проблему: кто должен реализовывать проект и получить выигрыш −1, если другой может выступить в роли «безбилетника» и иметь выигрыш 6?
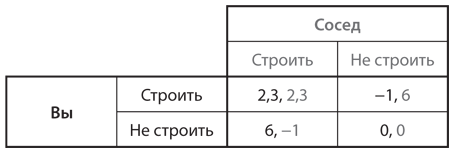
Рис. 11.2. Коллективное действие в контексте дилеммы заключенных: версия II
Б. Коллективное действие в игре в труса
Еще одно изменение показателей исходной дилеммы заключенных (см. ) меняет сам характер игры. Допустим, издержки в связи с выполнением работы сократятся до уровня, при котором вам лучше самому построить систему орошения, если этого не сделает сосед. В частности, предположим, что реализация проекта одним человеком требует 4 недели работы, а значит, C(1) = 4, а двумя людьми — по 3 недели на каждого, то есть C(2) = 3 (для каждого участника проекта); преимущества те же, что и раньше. На рис. 11.3 представлена матрица выигрышей с учетом этих изменений. Теперь ваш наилучший ответ сводится к уклонению от выполнения работы, если ваш сосед работает, и работе, если сосед уклоняется от нее. По своей структуре эта игра напоминает игру в труса, где уклонение от работы равносильно стратегии «ехать прямо» (жесткая, или некооперативная, стратегия), а выполнение — стратегии «свернуть» (примирительная, или кооперативная, стратегия).
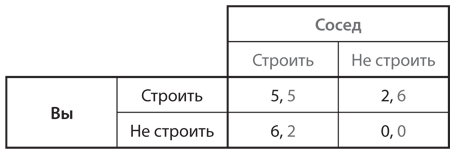
Рис. 11.3. Коллективное действие в контексте игры в труса: версия I
Если данная игра приведет к формированию одного из равновесий в чистых стратегиях, сумма выигрышей двух игроков составит 8, что меньше общего исхода, который они могли бы получить, если бы оба занялись строительством. Иными словами, ни одно из равновесий Нэша не обеспечивает всей группе такой выигрыш, как скоординированный исход, подразумевающий применение обоими фермерами стратегии «строить». Социальный оптимум дает общий выигрыш 10. Если исход этой игры в труса представляет собой равновесие в смешанных стратегиях, то два фермера окажутся в еще худшем положении, чем в случае любого из равновесий в чистых стратегиях: их общий выигрыш будет меньше 8 (а если точнее, 4).
Игра в труса, основанная на коллективном действии, может иметь еще одну структуру, если внести дополнительные изменения в выигрыши от реализации проекта. Как и в случае со второй версией дилеммы заключенных, допустим, что проект с участием двух человек ненамного лучше проекта с участием одного человека. Тогда каждый фермер получит от проекта с двумя участниками выгоду B(2), составляющую всего 6,3, а проект с участием одного человека по-прежнему обеспечит каждому из них выгоду B(1) = 6. Мы предлагаем вам применить полученные навыки и самостоятельно составить таблицы выигрышей в этой игре. Вы увидите, что это по-прежнему игра в труса (назовем ее игрой в труса II) и в ней, как и в предыдущей версии, есть два равновесия Нэша в чистых стратегиях, в каждом из которых только один фермер выбирает стратегию «строить», но сумма выигрышей в случае, если оба фермера выбирают «строить», равна всего 6,6, тогда как сумма выигрышей при выборе стратегии «строить» только одним фермером равна 8. Социальный оптимум сводится к тому, что реализовывать проект должен только один фермер. При этом каждый фермер предпочитает равновесие, при котором строит не он. Это может привести к новой динамической игре, в которой каждый фермер ждет, чтобы оросительную систему построил сосед. Или же исходная игра может обусловить равновесие в смешанных стратегиях с его низкими ожидаемыми выигрышами.
В. Коллективное действие в контексте игры в доверие
И наконец, давайте внесем несколько иные изменения в исходную дилемму заключенных, оставив преимущества от реализации проекта с участием двух человек на прежнем уровне и сократив выгоду от проекта с участием одного человека до B(1) = 3. Такое изменение настолько снижает ваши выгоды как «безбилетника», что если теперь ваш сосед выберет стратегию «строить», то ваш наилучший ответ — тоже «строить». На рис. 11.4 представлена таблица выигрышей в этой версии игры. Это игра в доверие с двумя равновесиями в чистых стратегиях: одно — когда вы совместно реализуете проект, а другое — когда оба этого не делаете.
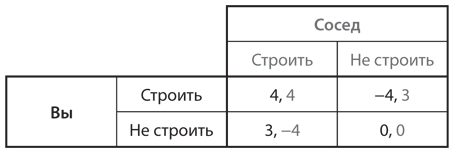
Рис. 11.4. Коллективное действие в контексте игры в доверие
Как и во второй версии игры в труса (II), оптимальный для всей группы исход представляет собой одно из двух равновесий Нэша. Но есть одно отличие. В версии игры в труса II игроки отдают предпочтение разным равновесиям, любое из которых обеспечивает социальный оптимум. В игре в доверие оба игрока предпочитают одно и то же равновесие, и это единственный исход, оптимальный для всей группы. Поэтому достичь социального оптимума в игре в доверие легче, чем в игре в труса.
Г. Коллективное бездействие
Структура выигрышей многих коллективных игр несколько отличается от выигрышей, представленных в примере с ирригационным проектом. Наши фермеры оказываются в ситуации, в которой социальный оптимум подразумевает, что по крайней мере один из них (если не оба) должен участвовать в проекте. Следовательно, в этой игре присутствует коллективное действие. Другие игры со многими участниками правильнее было бы назвать играми с коллективным бездействием. В таких играх общество в целом предпочитает, чтобы некоторые или все его члены не участвовали в игре, или не действовали. В качестве примеров подобного взаимодействия можно назвать выбор маршрутов передвижения в часы пик, выбор инвестиционных планов или районов рыбного промысла.
Общая характеристика всех этих игр состоит в том, что их участники должны решить, пользоваться ли им тем или иным общим ресурсом, будь то автомагистраль, высокодоходный инвестиционный фонд или водоем с большим количеством рыбы. Такие коллективные игры с «бездействием» больше известны как игры с распределением общих ресурсов: суммарный выигрыш всех участников достигает максимума, когда они воздерживаются от чрезмерного использования общих ресурсов. Проблема, связанная с неспособностью достичь социального оптимума в таких играх, известна как трагедия общин; термин, придуманный Гарретом Хардином в его статье с аналогичным названием.
Ранее мы исходили из того, что ирригационный проект обеспечивает вам и вашему соседу одинаковые преимущества. Но что если усилиями обоих фермеров построена система, расходующая так много воды, что им теперь нечем поить скот? Тогда выигрыш каждого из них может быть отрицательным и более низким, если оба выберут стратегию «строить», чем в случае стратегии «не строить». Это был бы еще один вариант дилеммы заключенных, о которой шла речь в и в которой социально оптимальный исход подразумевает, что ни один фермер не строит оросительную систему, хотя каждый по-прежнему в этом заинтересован. Или, предположим, деятельность одного фермера наносит ущерб другому, как это бы произошло, если бы единственным способом спасти одну ферму от затопления стал бы отвод воды на другую. При этом выигрыши обоих фермеров могли бы быть отрицательными, если бы сосед выбрал стратегию «строить». В такой ситуации могла бы возникнуть еще одна версия игры в труса, в которой каждый хочет строить оросительную систему, если другой к этому не стремится, тогда как для обоих было бы лучше, если бы проектом никто не занимался.
Проблемы, рассмотренные в этих примерах коллективного действия и коллективного бездействия, вам уже знакомы. Различные альтернативные способы их решения также соответствуют общим принципам, о которых шла речь в предыдущих главах. Но прежде чем анализировать решения, давайте посмотрим, как эти проблемы проявляются в более реалистичной среде, когда в таких играх одновременно взаимодействуют несколько игроков.
2. Проблемы коллективного действия в больших группах
В данном разделе мы расширим наш пример с ирригационным проектом на ситуацию, в которой каждый член группы из N фермеров должен решить, принимать ли в нем участие. Здесь нам пригодятся обозначения, введенные выше: C(n) — издержки, которые несет каждый фермер, когда n фермеров из общего количества N решают строить оросительную систему; B(n) — выгода каждого фермера независимо от его участия в проекте. При этом каждый участник проекта получает выигрыш P(n) = B(n) – C(n), а каждый уклоняющийся или предпочитающий не участвовать — выигрыш S(n) = B(n).
Предположим, вы озадачились вопросом, присоединяться к строительству оросительной системы или нет. Ваше решение будет зависеть от действий остальных (N – 1) фермеров, входящих в состав группы. В общем случае вам предстоит решить, когда из остальных (N – 1) фермеров n принимают участие в проекте, а (N – 1 – n) уклоняются от него. Если вы тоже намерены уклониться, количество участников проекта по-прежнему будет равно n, а значит, вы получите выигрыш S(n). Если предпочтете участвовать, количество участников составит n + 1 и вы получите выигрыш P(n + 1). Следовательно, ваш окончательный выбор зависит от сравнения этих двух выигрышей: вы будете строить, если P(n + 1) > S(n), и откажетесь, если P(n + 1) < S(n). Это сравнение применимо ко всем версиям коллективной игры, проанализированным в ; различия в поведении игроков в разных версиях возникают из-за изменений значений P(n + 1) и S(n) в связи с изменением структуры выигрышей.
Мы можем соотнести примеры игр с двумя участниками из с этой обобщенной схемой. Если в игре только два игрока, то P(2) — это выигрыш одного фермера от реализации проекта, когда другой тоже в нем участвует, а S(1) — выигрыш фермера, уклоняющегося от участия, если другой фермер строит оросительную систему, и т. д. Таким образом, мы можем обобщить таблицы выигрышей на рис. 11.1–11.4, представив их в алгебраической форме. Общая структура выигрышей показана на рис. 11.5.
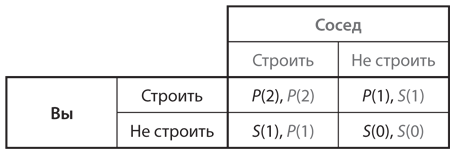
Рис. 11.5. Общая форма игры с коллективным действием с двумя участниками
Игра, отображенная на рис. 11.5, — это дилемма заключенных, если одновременно выполняются следующие неравенства:
P(2) < S(1), P(1) < S(0), P(2) > S(0).
Согласно первому неравенству, наилучший ответ на стратегию «строить» — «не строить», согласно второму — наилучший ответ на стратегию «не строить» также «не строить», а третьему — что для обоих игроков комбинация стратегий «строить»/«строить» предпочтительнее комбинации «не строить» / «не строить». Это дилемма типа I, если 2P(2) > P(1) + S(1), а значит, общий выигрыш больше, когда оба фермера решают строить, чем когда строительством занимается только один. Вы можете составить аналогичные неравенства, описывающие выигрыши, которые обеспечивают другие типы игр, представленные в .
Теперь вернемся к версии игры с участием n игроков. Воспользовавшись функциями выигрышей в случае двух действий, P(n + 1) и S(n), мы можем построить графики, которые помогут нам определить, с каким типом игры мы имеем дело, а также найти в ней равновесие Нэша, которое затем сможем сравнить с социально оптимальным исходом игры.
А. Дилемма заключенных со многими участниками
Рассмотрим конкретную версию игры со строительством оросительной системы, в которой 100 фермеров из одной деревни решают, какое действие предпринять. Допустим, реализация ирригационного проекта позволит повысить продуктивность земельных угодий каждого фермера пропорционально масштабу проекта; в частности, предположим, что выгода каждого фермера при участии n человек в строительстве составляет P(n) = 2n. Представим также, что, если вы не участвуете в проекте, у вас все равно есть возможность воспользоваться его преимуществами, а сэкономленное время потратить на что-то другое, чтобы заработать еще 4, то есть S(n) = 2n + 4. Не забывайте, что ваше решение об участии в проекте зависит от относительной величины P(n + 1) = 2(n + 1) и S(n) = 2n + 4. Два отдельных графика этих функций для каждого отдельного фермера показаны на рис. 11.6, где значения n от 0 до (N – 1) отображены на горизонтальной оси, а на вертикальной — выгода фермера. Если в данный момент в проекте участвует не так много фермеров (а значит, большинство из них уклонились), ваш выбор будет зависеть от относительного положения P(n + 1) и S(n) с правой стороны графика.
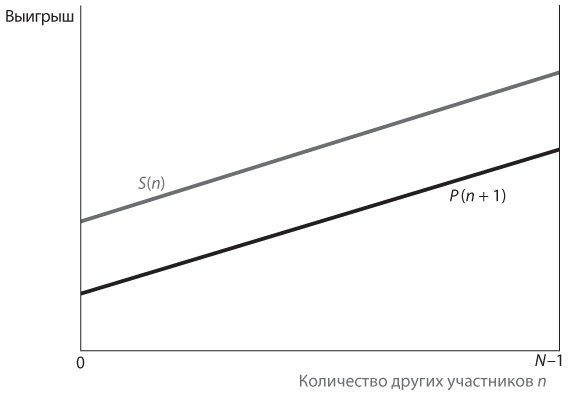
Рис. 11.6. График выигрышей в дилемме заключенных со многими участниками
Поскольку на самом деле n принимает только целые значения, технически каждая из функций P(n + 1) и S(n) состоит из дискретного множества точек, а не из непрерывного множества, как подразумевают сглаженные линии на рисунке. Но при большом значении N эти дискретные точки находятся достаточно близко друг от друга, поэтому мы можем их соединить и представить каждую функцию выигрыша в виде непрерывной линии. Кроме того, мы также используем в этом разделе линейные функции P(n + 1) и S(n), для того чтобы сформулировать основные идеи, а более сложные возможности обсудим чуть позже.
Напомним, что вы определяете свой выбор с учетом количества текущих участников проекта n и выигрышей, связанных с каждым действием при таком значении n. На проиллюстрирован случай, когда линия S(n) находится полностью над линией P(n + 1). Следовательно, каким бы ни было число других участников (то есть каким бы большим ни было значение n), если вы откажетесь от проекта, ваш выигрыш будет выше, чем в случае согласия. Стало быть, отказ от участия в проекте — ваша доминирующая стратегия. У всех игроков одинаковые выигрыши, а значит, отказ от участия в проекте — доминирующая стратегия каждого игрока. Таким образом, равновесие Нэша в этой игре подразумевает, что все игроки станут уклоняться и оросительная система так и не будет построена.
Обратите внимание, что обе линии поднимаются по мере увеличения n. Какое бы действие вы ни выбрали, вам выгодно, чтобы в проекте участвовало больше фермеров. Левая точка пересечения линии S(n) с вертикальной осью находится ниже правой точки пересечения линии P(n + 1), то есть S(0) = 4 < P(N) = 102. Это говорит о том, что, если все фермеры (в том числе и вы) откажутся от строительства, выигрыш каждого из них (в том числе ваш) будет меньше, чем в случае согласия. Все фермеры добились бы более весомых результатов, чем при равновесии Нэша, если бы можно было обеспечить исход, при котором каждый из них участвует в проекте. Это и делает игру дилеммой заключенных.
Чем равновесие Нэша, найденное с помощью графика на , отличается от социального оптимума в этой игре? Для того чтобы ответить на данный вопрос, понадобится способ описать общий социальный выигрыш при каждом значении n; мы сделаем это с помощью функций выигрышей P(n) и S(n), чтобы построить третью функцию T(n), отображающую общий выигрыш для общества от проекта с n участниками как функцию n. Он состоит из значения P(n) для каждого из n участников проекта и значения S(n) для каждого из (N – n) тех, кто отказался от участия:
T(n) = nP(n) + (N – n)S(n).
Социальный оптимум наблюдается в случае, когда соотношение между участниками проекта и отказавшимися от него максимизирует общий выигрыш T(n), или при таком количестве участников проекта (то есть при таком значении n), которое максимизирует T(n). Для того чтобы лучше понять, каким может быть этот показатель, удобнее записать T(n) иначе, преобразовав представленное выше выражение в такое равенство:
T(n) = NS(n) – n[S(n) – P(n)].
Этот вариант функции общего социального выигрыша показывает, что мы можем его вычислить, если дадим каждому из N человек выигрыш уклонившегося от строительства, а затем отнимем дополнительную выгоду [S(n) – P(n)] отказавшихся у каждого из n участников проекта.
В играх с коллективным действием, в отличие от игр с распределением общих ресурсов, мы обычно ожидаем, что значение S(n) будет расти по мере увеличения n. Следовательно, значение первого члена выражения, NS(n), также возрастает при увеличении n. Если второй член выражения не увеличивается слишком быстро при увеличении n (как было бы, если бы дополнительная выгода [S(n) – P(n)] человека, отказавшегося от участия в проекте, представляла собой небольшую и постоянную величину), то эффект первого члена доминирует в определении значения T(n).
Именно это происходит с функцией общего социального выигрыша в нашем примере с сотней фермеров. Здесь T(n) = nP(n) + (N – n)S(n) преобразуется в T(n) = n(2n) + (100 – n)(2n + 4) = 2n2 + 200n – 2n2 + 400 – 4n = 400 + 196n. В данном случае T(n) постепенно увеличивается вместе с n и достигает максимального значения при n = N, когда никто не уклоняется от участия в проекте.
Версия игры с большой группой участников позволяет сделать тот же вывод, что и раньше. Группа фермеров в целом выиграла бы, если бы все фермеры строили оросительную систему, то есть если n = N. Но структура выигрышей такова, что у каждого фермера есть стимул уклониться от этого. Равновесие Нэша в игре (при n = 0) не будет социально оптимальным. Поиск способов достижения социального оптимума — один из важнейших вопросов в области изучения коллективного действия; мы вернемся к нему ниже в данной главе.
В других ситуациях функция T(n) может иметь максимум при другом значении n, а не только при n = N. Иными словами, совокупный выигрыш общества можно максимизировать, допустив определенное уклонение от участия в проекте. Даже в случае дилеммы заключенных необязательно должно быть так, что функция общего выигрыша достигает максимума при максимальном значении n. Если разрыв между S(n) и P(n) растет достаточно быстро при увеличении значения n, то отрицательный эффект второго члена выражения для T(n) перевешивает положительный эффект первого члена выражения по мере приближения n к N; в таком случае лучше всего позволить людям уклониться — другими словами, социально оптимальное значение n может быть меньше N. Этот результат идентичен полученному в ходе анализа второй версии дилеммы заключенных в .
Такой исход мы наблюдали бы в нашей деревне, если бы значение S(n) составляло 4n + 4, а не 2n + 4. Тогда T(n) = –2n2 + 396n + 400, что больше не является линейной функцией n. На самом деле графический калькулятор или простейшие расчеты позволяют определить, что в данном случае T(n) принимает максимальное значение при n = 99, а не n = 100, как ранее. Изменение структуры выигрышей создало в них неравенство (уклонившиеся от участия в проекте находятся в более выгодном положении, чем его участники), что добавляет еще одну трудность к попыткам общества решить эту дилемму. К примеру, как деревне выбрать одного фермера на роль уклониста?
Б. Игра в труса со многими участниками
Теперь рассмотрим ряд других конфигураций выигрышей. Например, когда P(n) = 4n + 36, а значит, P(n + 1) = 4n + 40 и S(n) = 5n, две линии выигрышей пересекутся. Этот случай показан на рис. 11.7. Здесь при малых значениях n P(n + 1) > S(n), то есть если некоторые фермеры участвуют в проекте, вам также лучше участвовать. При больших значениях n P(n + 1) < S(n), то есть если многие фермеры участвуют в проекте, вам лучше этого не делать. Обратите внимание, что эти утверждения эквивалентны идее игры в труса из двух человек, согласно которой «вы уклоняетесь, если ваш сосед работает, и работаете, если сосед уклоняется». Этот случай действительно представляет собой игру в труса. В более общем плане игра в труса происходит, когда у вас есть выбор из двух действий и вы предпочитаете делать то, что большинство других игроков предпочитают не делать.
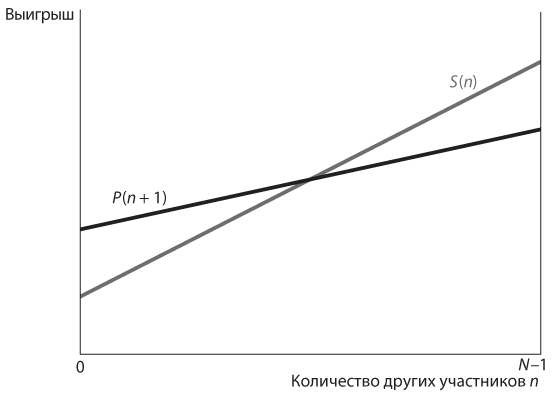
Рис. 11.7. График выигрышей в игре в труса со многими участниками
Кроме того, рис. 11.7 поможет нам определить положение равновесия Нэша в этой версии игры. Поскольку вам выгодно участвовать в проекте при малых значениях n и отказаться при больших значениях n, то равновесие должно быть при каком-то промежуточном значении n. Вам безразлично, какой именно из двух вариантов выбрать, только при значении n, при котором две линии пересекаются. Точка пересечения соответствует равновесному значению n. На нашем графике P(n + 1) = S(n), когда 4n + 40 = 5n, или когда n = 40; это и есть соответствующее равновесию Нэша количество фермеров, которые будут строить оросительную систему.
Если две линии пересекаются в точке, соответствующей целому значению n, это и будет количество участников проекта согласно равновесию Нэша. Если это не так, то, строго говоря, в игре нет равновесия Нэша. Но на практике, если текущее значение n в данной комбинации — целое число, расположенное сразу же слева от точки пересечения (которая может не быть целым числом), то еще один фермер захочет присоединиться к проекту, а если текущее значение n — целое число, расположенное справа от точки пересечения, то один фермер захочет уклониться от него. Следовательно, количество участников будет находиться в непосредственной близости от точки пересечения, и мы можем с полным основанием утверждать, что она и будет равновесием в приближенном смысле.
Структура выигрышей на показывает, что обе линии имеют положительный наклон, хотя это и необязательно. Можно предположить, что выгода каждого человека уменьшается, когда в проекте участвует больше людей, поэтому линии могут иметь отрицательный наклон. Игре в труса с коллективным действием присуща одна важная особенность: когда всего несколько человек выполняют одно действие, любому другому человеку также лучше его выполнять; когда одно действие выполняет много людей, то другому человеку лучше делать что-то иное.
В чем состоит социально оптимальный исход в игре в труса с коллективным действием? Если выигрыш каждого участника проекта P(n) возрастает по мере увеличения числа участников, а выигрыш каждого уклониста S(n) не сильно превышает P(n) каждого участника, то общий социальный выигрыш достигнет максимума, если все участвуют в проекте. Это и есть исход игры в нашем примере, где T(n) = 536n – n2; общий социальный выигрыш увеличивается по n до значения N (в данном случае 100), а значит, n = N — это и есть социальный оптимум.
Однако в более общем плане некоторые варианты игры в труса приведут к социальным оптимумам, в которых лучше допустить определенное уклонение от участия в проекте. Если бы в группе было 300, а не 100 фермеров, мы получили бы именно такой исход. Социально оптимальное количество участников проекта, вычисленных с помощью графического калькулятора или простейших расчетов, составило бы 268. В этом и заключается разница между версиями I и II игры в труса в примере, о котором шла речь в . В качестве упражнения вы можете попытаться найти структуру выигрышей, которая приведет к такому исходу в деревне с сотней фермеров. В аналогичных более общих вариантах игры в труса оптимальное количество участников может быть даже меньше, чем в случае равновесия Нэша. В мы более подробно проанализируем вопрос о социальном оптимуме во всех этих версиях игры.
В. Игра в доверие со многими участниками
И наконец, рассмотрим третий возможный тип игр с коллективным действием, а именно игру в доверие. На рис. 11.8 представлены графики выигрышей для такой игры, где мы исходим из предположения, что фермеры получают P(n + 1) = 4n + 4 и S(n) = 2n + 100. Здесь S(n) > P(n + 1) при малых значениях n, поэтому, если оросительную систему строят не так уж много фермеров, вам также нужно уклониться от участия в проекте. Но P(n + 1) > S(n) при больших значениях n; тогда, если многие фермеры участвуют в строительстве, вам тоже лучше к ним присоединиться. Иными словами, в отличие от игры в труса, игра в доверие — это игра с коллективным действием, в которой вам необходимо сделать тот же выбор, что и другие ее участники.
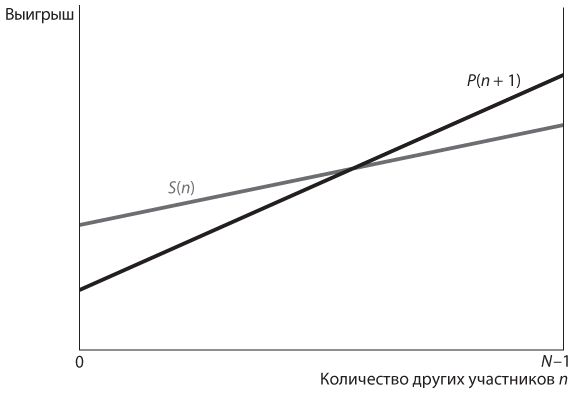
Рис. 11.8. График выигрышей в игре в доверие со многими участниками
За исключением обозначений, график на рис. 11.8 практически идентичен графику на . Однако положение точки, соответствующей равновесию Нэша, в значительной мере зависит от того, как именно обозначены две линии на графике. На рис. 11.8 показано, что при любом начальном значении n, расположенном слева от пересечения, каждый фермер захочет отказаться от участия в проекте и равновесие Нэша будет достигнуто при n = 0, когда все фермеры уклоняются. Однако справа от точки пересечения складывается прямо противоположная картина. Из этой части графика видно, что каждый фермер пожелает участвовать в строительстве, поэтому в игре сформируется еще одно равновесие Нэша при n = N.
Технически в этой игре существует еще и третье равновесие Нэша, если значение n в точке пересечения целое число, как в нашем примере. Тогда мы можем определить, что P(n + 1) = 4n + 4 = 2n + 100 = S(n) при n = 48. Следовательно, если бы n было в точности равно 48, мы увидели бы исход, при котором одни фермеры решили бы реализовывать проект, а другие нет. Эта ситуация могла бы стать равновесием только при таком значении n, но даже тогда она была бы крайне нестабильной. Если бы всего один фермер случайно присоединился не к той группе, его выбор изменил бы стимулы всех остальных фермеров, что привело бы всю игру к одному из равновесий в конечных точках графика. Это и есть два устойчивых равновесия Нэша в данной игре.
Социальный оптимум в этой игре достаточно легко обнаружить на графике на . Поскольку обе линии на нем восходящие (то есть для каждого члена группы лучше, если в проекте примет участие больше людей), очевидно, что равновесие, которое находится у правого края графика, более благоприятно для всей группы. В нашем примере это подтверждается тем, что значение T(n) = 2n2 + 100n + 10 000 возрастает по n при всех положительных значениях n; следовательно, социально оптимальное значение n — это максимальное значение, или n = N. Стало быть, в игре в доверие социально оптимальный исход — это одно из устойчивых равновесий Нэша. В связи с этим получить его может быть даже легче, чем в ряде других случаев. Однако независимо от того, отображает ли он равновесие Нэша в исходной игре, остается актуальным вопрос, как все это осуществить на практике.
До сих пор в наших примерах фигурировали относительно небольшие группы людей, от 2 до 100 человек. Но когда общая численность группы N достаточно большая, один человек оказывает совсем незначительное влияние на ситуацию, поэтому значение P(n + 1) почти равно значению P(n). Таким образом, условие, при котором любой человек предпочтет уклониться от участия в проекте, выглядит так: P(n) < S(n). Выразив это неравенство в выгодах и издержках в связи с общим проектом из нашего примера (а именно P(n) = B(n) – C(n) и S(n) = B(n)), мы увидим, что значение P(n) (в отличие от P(n + 1) в наших предыдущих расчетах) всегда меньше S(n); отдельные люди постоянно будут стремиться к уклонению от участия в проекте, когда значение N очень большое. Поэтому проблемы коллективной реализации общественных проектов в крупной группе почти всегда проявляются в виде дилеммы заключенных. Однако, как мы уже заметили, такой результат не обязательно будет достигаться в небольших группах. То же касается и больших групп в других контекстах, таких как пробки на дорогах, которые мы обсудим немного ниже в данной главе.
В общем мы должны предусмотреть возможность более широкой интерпретации выигрышей P(n) и S(n), чем в представленном выше конкретном примере, учитывающем преимущества и издержки в связи с проектом. Скажем, мы не можем предположить, что функции выигрышей всегда будут линейными. Дело в том, что в самом общем случае P(n) и S(n) могут быть любыми функциями n, графики которых могут неоднократно пересекаться. При этом может присутствовать множество равновесий, хотя каждое из них может представлять один из описанных выше типов. Кроме того, некоторые игры будут отнесены к категории игр с распределением общих ресурсов, поэтому в случае полностью обобщенных игр мы будем говорить о двух действиях, обозначенных символами P и S, которые не обязательно будут означать «участие в проекте» и «отказ от участия в проекте», но это позволит нам использовать для обозначения выигрышей те же символы. Таким образом, когда n игроков совершают действие P, P(n) — это выигрыш каждого игрока, выполняющего действие P, а S(n) — выигрыш каждого игрока, выполняющего действие S.
3. Внешние эффекты, или экстерналии
До сих пор мы видели, что коллективные игры проходят в контексте дилеммы заключенных, игры в труса или игры в доверие. Мы также видели, что равновесия Нэша в этих играх редко обеспечивают социально оптимальный уровень участия (или его ограничения). И даже когда социальный оптимум и равновесие Нэша совпадают, это, как правило, лишь одно из возможных равновесий, которые могут присутствовать в игре. Теперь мы глубже проанализируем различия между индивидуальными (или личными) и групповыми (или социальными) стимулами в таких играх. Кроме того, подробнее опишем воздействие решений каждого человека на других людей и группу в целом. Этот анализ совершенно четко объясняет наличие таких различий между стимулами, то, как они проявляются и что можно предпринять для достижения более благоприятных в социальном отношении исходов игры, чем в случае равновесия Нэша.
А. Поездки на работу и обратно и сопутствующие эффекты
Сначала давайте представим себе большую группу из 8000 жителей пригорода, которые ежедневно ездят в город на работу и обратно. Будучи одним из ее членов, вы можете выбрать для поездки либо скоростную магистраль (действие P), либо сеть местных дорог (действие S). Поездка по местным дорогам неизменно занимает 45 минут, сколько бы автомобилей по ним ни перемещалось. На поездку по скоростной автомагистрали уходит всего 15 минут при условии отсутствия заторов. Однако каждый водитель, выбирающий скоростную магистраль, увеличивает время в пути любого другого водителя, который поедет по этому маршруту, на 0,005 минуты (около одной четверти секунды).
Выигрыши в игре исчисляются в минутах сэкономленного времени — например, на сколько минут время поездки туда и обратно меньше одного часа. Следовательно, выигрыш водителей, обозначаемый как S(n), выбравших маршрут по местным дорогам, — постоянная величина: 60 – 45 = 15, независимо от значения n. Однако выигрыш водителей — P(n), — выбравших скоростную автомагистраль, зависит от значения n; в частности, P(n) = 60 – 15 = 45 при n = 0, но значение P(n) падает на 5 / 1000 (или 1 / 200) в случае каждого, кто выбирает автомагистраль для поездки на работу и обратно. С учетом этого, P(n) = 45 – 0,005n. Графики двух функций выигрышей представлены на рис. 11.9.
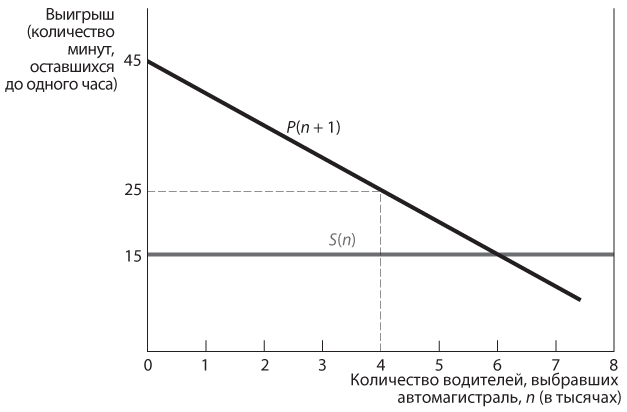
Рис. 11.9. Игра в выбор маршрута для поездки на работу и обратно
Предположим, сначала на автомагистрали находится 4000 автомобилей, то есть n = 4000. При таком количестве машин на дороге каждому водителю требуется 15 + 4000 × 0,005 = 15 + 20 = 35 минут, чтобы добраться на работу; при этом каждый из них получает выигрыш P(n) = 25 [60 – 35, то есть P(4000)]. Как показано на рис. 11.9, этот выигрыш лучше, чем тот, который получат водители, выбравшие местные дороги. В итоге вы, будучи одним из них, можете принять решение переключиться с поездки по местным дорогам на поездку по скоростной автомагистрали. Выбор нового маршрута увеличит значение n на 1, что скажется на выигрышах остальных участников движения. Теперь количество водителей, выбравших автомагистраль, составляет 4001 (в том числе и вы), а время поездки каждого равно 35 + 5 / 200, или 35,005 минуты. При этом каждый водитель получит выигрыш P(n + 1) = P(4001) = 24,995, по-прежнему превышающий выигрыш от поездки по местным дорогам. Следовательно, у вас есть личный стимул изменить маршрут, поскольку P(n + 1) > S(n) (24,995 > 15).
Выбор другого маршрута приносит вам личную выгоду (которую получаете только вы), эквивалентную разности между вашими выигрышами до и после такого перехода; она составляет P(n + 1) – S(n) = 9,995 минуты. Поскольку вы — один человек, а значит, малая часть группы, полученная вами выгода в виде увеличения выигрыша в сравнении с общим выигрышем всей группы весьма небольшая, или маржинальная. В связи с этим мы называем ее маржинальной личной выгодой.
Однако теперь из-за вашего решения изменить маршрут каждому из 4000 других водителей, выбравших автомагистраль, придется тратить на поездку на 0,005 минуты больше. Это означает, что выигрыш каждого из них меняется на P(4001) – P(4000) = –0,005. Водители, выбравшие местные дороги, также столкнутся с изменением выигрышей в размере S(4001) – S(4000), но в нашем примере это равно нулю. Суммарное воздействие вашего решения на всех остальных водителей составляет 4000 × (–0,005) = –20. Ваше действие, то есть переход с местных дорог на скоростную автомагистраль, повлияло на выигрыши других игроков. Всякий раз, когда действие одного человека оказывает подобное влияние на других людей, наблюдается сопутствующий эффект, или внешний эффект, или экстерналия. Следует отметить, что, поскольку вы представляете собой не более чем малую часть всей группы, ваше воздействие на ее членов следует называть маржинальным сопутствующим эффектом.
Совокупность таких факторов, как маржинальная личная выгода и маржинальный сопутствующий эффект, и есть полное воздействие вашего решения перейти на другой маршрут на группу людей, совершающих поездки на работу и обратно, или общее предельное изменение выигрыша группы или общества в целом. Мы называем данный показатель маржинальной социальной выгодой, связанной с выбором вами другого маршрута. В действительности эта «выгода» может быть положительной или отрицательной, поэтому само слово «выгода» в данном контексте не означает, что все случаи перехода на другой маршрут пойдут на пользу всей группе. В нашем примере общая предельная социальная выгода составляет 9,995 – 20 = –10,005 минуты. Следовательно, общий социальный эффект вашего перехода на другой маршрут носит негативный характер: в целом социальный выигрыш уменьшается более чем на 10 минут.
Б. Сопутствующие эффекты: общий случай
Мы можем описать эффекты, наблюдаемые в примере с поездками на работу и обратно, в еще более обобщенном виде с помощью функции социального выигрыша T(n), где n — количество людей, выбравших P, а значит, N – n — это число людей, выбравших S. Предположим, что сначала n людей выбрали P, а также что один человек переключается с S на P. Тогда количество людей, выбравших P, увеличивается на величину от 1 до (n + 1), а количество людей, выбравших S, уменьшается на величину от 1 до (N – n – 1). Таким образом, общий социальный выигрыш составляет
T(n + 1) = (n + 1)P(n + 1) + [N – (n + 1)] S (n + 1).
Увеличение общего социального выигрыша равно разности между T(n + 1) и T(n). После приведения и перестановки членов получим следующее уравнение:
T(n + 1) – T(n) = (n + 1) P(n + 1) + [N – (n + 1)] S (n + 1) – nP(n) – (N – n)S(n) =
[P(n + 1) – S (n)] + n[P(n + 1) – P(n)] + [N – (n + 1)][S(n + 1) – S(n)]. (11.1)
Уравнение (11.1) математически описывает различные эффекты перехода одного человека с S на P, которые мы наблюдали в примере с поездками на работу и обратно. Это уравнение показывает, как предельная социальная выгода делится на предельные изменения выигрышей подгрупп общей совокупности.
Первый из трех членов уравнения () (а именно [P(n + 1) – S (n)]) — это маржинальная личная выгода, полученная человеком, переключающимся на другое действие. Как мы видели выше, именно этот член уравнения определяет выбор человека, причем все отдельные варианты такого выбора образуют равновесие Нэша.
Второй и третий члены уравнения () — количественная оценка сопутствующих эффектов, связанных с влиянием перехода одного человека на всех остальных участников группы. У каждого из n человек, выбравших P, выигрыш меняется на величину [P(n + 1) – P(n)], если еще один человек переключается на P; этот сопутствующий эффект можно наблюдать во второй группе членов уравнения (). После перехода одного человека на другое действие остается еще N – (n + 1), или N – n – 1, других участников группы, которые по-прежнему выбирают S, причем каждый из них видит, что его выигрыш меняется на [S(n + 1) – S(n)]; этот сопутствующий эффект отображен в третьей группе членов уравнения. Безусловно, выбор одним водителем другого маршрута оказывает совсем незначительное влияние на время пребывания остальных участников движения в пути, однако когда их на дороге очень много (то есть при большом значении N), совокупный сопутствующий эффект может быть достаточно большим.
Таким образом, мы можем записать уравнение () при переходе одного человека с S на P или с P на S как:
Маржинальная социальная выгода = маржинальная личная выгода + маржинальный сопутствующий эффект.
В примере, в котором один человек переходит с S на P, мы имеем:
Маржинальная социальная выгода = T(n + 1) – T(n),
Маржинальная личная выгода = P(n + 1) – S(n),
Маржинальный сопутствующий эффект = n[P(n + 1) – P(n)] + [N – (n + 1)] × [S(n + 1) – S(n)].
Применение дифференциального исчисления к формулам общего случая. Прежде чем более подробно рассматривать некоторые ситуации с наличием сопутствующего эффекта, чтобы понять, что можно сделать для обеспечения социально оптимальных исходов, мы сформулируем общие концепции этого анализа на языке дифференциального исчисления. Если вы не знаете этого языка, можете опустить оставшуюся часть данного раздела, не рискуя нарушить целостность изложенного здесь материала. Если же знаете, альтернативная формулировка покажется вам проще и понятнее, чем представленные выше алгебраические преобразования.
Если общее количество N членов группы очень большое (например, исчисляется в сотнях или тысячах), то одного человека можно воспринимать как совсем небольшую, или бесконечно малую, часть целого. Это позволяет рассматривать n как непрерывную переменную. Если T(n) — общий социальный выигрыш, мы вычислим эффект от изменения n, проанализировав увеличение бесконечно малой предельной величины dn вместо увеличения на целую единицу с n до (n + 1). В первом приближении изменение выигрыша составляет T´(n)dn, где T´(n) — производная от T(n) по n. Воспользовавшись выражением для общего социального выигрыша
T(n) = nP(n) + (N – n)S(n)
и продифференцировав это выражение, получим
T´(n) = P(n) + nP´(n) – S´(n) + (N – n)S´(n) = [P(n) – S(n)] + nP(n) + (N – n)S´(n). (11.2)
Это эквивалент уравнения (), выраженный в терминах дифференциального исчисления. T´(n) — это маржинальная социальная выгода. Маржинальная личная выгода равна P(n) – S(n), что представляет собой изменение выигрыша человека от перехода с S на P. В уравнении () оно было представлено как P(n + 1) – S(n), теперь же мы имеем P(n) – S(n). Это объясняется тем, что прибавление бесконечно малой величины dn к группе из n человек, выбравших P, не приводит к существенному изменению выигрыша ни одного из них. Тем не менее общее изменение их выигрыша, равное nP´(n), представляет достаточно большую величину и учитывается в вычислении сопутствующего эффекта — это второй член в уравнении (), — так же как и изменение выигрыша (N – n) человек, выбравших S, то есть (N – n)S´(n), третий член уравнения (). Два последних члена уравнения представляют собой предельный сопутствующий эффект.
В примере с поездками на работу и обратно у нас были такие значения: P(n) = 45 – 0,005n и S(n) = 15. Далее с помощью вычислений мы пришли к выводу, что предельная личная выгода каждого водителя, выбирающего автомагистраль, когда n водителей уже движутся по ней, составляет P(n) – S(n) = 30 – 0,005n. Поскольку P´(n) = –0,005, а S´(n) = 0, сопутствующий эффект составляет n × (–0,005) + (N – n) × 0 = –0,005n, что равно −20 при n = 4000. Ответ такой же, как и раньше, но дифференциальное исчисление упрощает процесс его получения и помогает найти оптимум непосредственно.
В. Еще раз о поездках на работу и обратно: отрицательные экстерналии
Отрицательная экстерналия наблюдается в случае, когда действие одного человека снижает выигрыши других членов группы, что перекладывает на них часть дополнительных затрат. Мы наблюдали это в примере с поездками на работу и обратно, где предельный сопутствующий эффект от перехода одного человека на автомагистраль был отрицательным, поскольку увеличивал время поездки других участников движения на 20 минут. Однако человек, меняющий маршрут поездки на работу, не учитывает сопутствующий эффект (экстерналию); его мотивируют только собственные выигрыши. (Не забывайте, что чувство вины, которое он может испытывать в связи с причинением вреда окружающим, уже должно быть отображено в его выигрышах.) Такой человек изменит свое действие с S на P, если это позволит ему получить положительную маржинальную личную выгоду. Тогда это изменение поставит его в более выгодное положение.
Однако общество в целом бы выиграло, если бы решения человека, регулярно совершающего поездки из пригорода на работу и обратно, зависели от маржинальной социальной выгоды. В нашем примере она имеет отрицательное значение –10,005, тогда как маржинальная личная выгода — положительное 9,995, поэтому отдельный водитель переходит с местных дорог на автомагистраль, даже если для общества было бы лучше, чтобы он этого не делал. В общем, в ситуациях с отрицательными экстерналиями маржинальная социальная выгода меньше маржинальной личной выгоды, что объясняется существованием отрицательного сопутствующего эффекта. Люди принимают решения на основании расчетов издержек и преимуществ, что неправильно с точки зрения общества. В итоге отдельные люди выбирают действия с отрицательным сопутствующим эффектом чаще, чем того хотело бы общество.
Уравнение () можно использовать для определения точных условий, при которых переход приносит выгоду одному человеку, в отличие от всей группы. Вспомните, что если n человек уже пользуются скоростной автомагистралью, а один водитель планирует перейти на нее с местных дорог, он получит от этого выгоду, если P(n + 1) > S(n), тогда как социальный выигрыш увеличивается при условии, что T(n + 1) – T(n) > 0. Личный выигрыш имеет положительное значение, если
45 – (n + 1) × 0,005 > 15,
44,995 – 0,005n > 15,
n < 200 (44,995 – 15) = 5999.
При этом социальная выгода имеет положительное значение при выполнении следующего условия:
45 – (n + 1) × 0,005 – 15 – 0,005n > 0,
29,995 – 0,01n > 0,
n < 2999,5.
Таким образом, при наличии свободы выбора люди, которые регулярно ездят из пригорода на работу и обратно, выберут маршрут, пролегающий по скоростной автомагистрали, пока их число не достигнет 6000, но при этом любое количество, превышающее 3000, сокращает общий социальный выигрыш. Для всей совокупности водителей было бы лучше, если бы их количество не превышало 3000.
Этот результат представлен в виде графика на рис. 11.10; он дублирует , но с добавлением линий маржинальной личной и социальной выгоды. Две линии, соответствующие функциям P(n + 1) и S(n), пересекаются в точке n = 5999, иными словами, в точке, соответствующей такому значению n, при котором P(n + 1) = S(n), то есть при котором маржинальная личная выгода равна нулю. В любой точке слева от этого значения n каждый отдельно взятый водитель, пользующийся местными дорогами, может подсчитать, что он получит положительную выгоду от перехода на автомагистраль. По мере совершения водителями такого перехода количество автомобилей на автомагистрали увеличивается — значение n повышается, так же как и в примере, о котором шла речь в . Напротив, справа от точки пересечения (то есть при n > 5999) S(n) > P(n + 1), а значит, каждый из (n + 1) водителей, пользующихся автомагистралью, получит выгоду от перехода на местные дороги. И по мере того как некоторые водители действительно начнут это делать, количество автомобилей на автомагистрали будет сокращаться, а значение n падать. Слева от точки пересечения этот процесс сходится к n = 5999, а справа — к 6000.
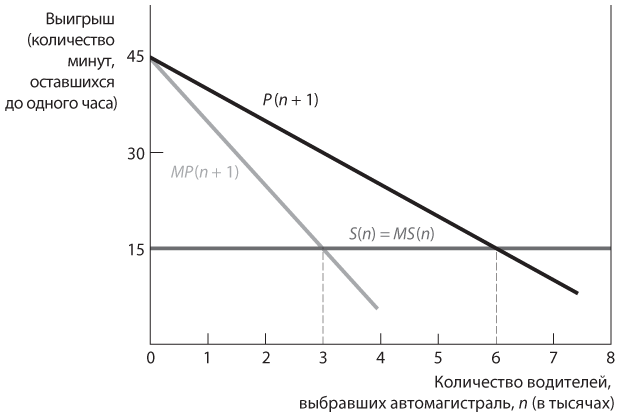
Рис. 11.10. Равновесие и оптимум в игре в выбор маршрута для поездки на работу и обратно
При использовании подхода, основанного на дифференциальном исчислении, мы бы рассматривали 1 как малое приращение n и построили бы график P(n) вместо P(n + 1). Тогда точкой пересечения было бы значение n = 6000, а не 5999. Очевидно, что на практике это фактически не играет роли. То есть мы можем назвать n = 6000 равновесием Нэша в игре с изменением маршрута в случае, когда выбор обусловлен сугубо личными соображениями. При наличии свободы выбора из 8000 человек, которые регулярно ездят из пригорода на работу и обратно, 6000 выберут скоростную автомагистраль и только 2000 будут ездить по местным дорогам.
Однако мы также можем представить исход этой игры с точки зрения всех жителей пригородной зоны. В целом они выигрывают от увеличения количества водителей n, пользующихся автомагистралью, если T(n + 1) – T(n) > 0, и проигрывают от увеличения n, если T(n + 1) – T(n) < 0. Для того чтобы разобраться, как это отобразить на графике, сформулируем идею несколько иначе. В частности, перепишем уравнение (), разбив его на два фрагмента, один из которых зависит только от P, а другой — только от S:
T(n + 1) – T(n) = (n + 1)P(n + 1) + [N – (n + 1)]S(n + 1) – nP(n) – [N – n]S(n) = S(n){P(n + 1) + n[P(n + 1) – P(n)]} – {S(n) + [N – (n + 1)][S(n + 1) – S(n)]}.
Выражение в первой группе скобок — это воздействие на выигрыши членов группы, выбравших P; в него входит P(n + 1) человек, перешедших на другой маршрут, а также сопутствующий эффект n[P(n + 1) – P(n)], отражающий влияние на всех остальных n человек, выбравших P. Мы называем это маржинальным социальным выигрышем подгруппы, выбравшей P, в случае если ее численность увеличивается с n до n + 1, или сокращенно MP(n + 1). Аналогично, выражение во второй группе скобок — маржинальный социальный выигрыш подгруппы, выбравшей S, или сокращенно MS(n). В итоге все выражение для T(n + 1) – T(n) говорит о том, что общий социальный выигрыш увеличивается, когда один человек переходит с S на P (или уменьшается, когда один человек переключается с P на S), если MP(n + 1) > MS(n), и уменьшается, когда один человек переходит с S на P (или увеличивается, когда один человек переключается с P на S), если MP(n + 1) < MS(n).
Воспользовавшись выражениями для P(n + 1) и S(n) в примере с поездками на работу и обратно, получим
MP(n + 1) = 45 – (n + 1) × 0,005 + n × (–0,005) = 44,995 – 0,01n.
При этом MS(n) = 15 для всех значений n. На представлены также графики функций MP(n + 1) и MS(n). Обратите внимание, что MS(n) везде совпадает с S(n), поскольку на местных дорогах не бывает заторов. Однако линия MP(n + 1) находится под линией P(n + 1). Из-за отрицательного сопутствующего эффекта социальная выгода от перехода одного человека на автомагистраль меньше его личной выгоды.
Графики MP(n + 1) и MS(n) пересекаются в точке n = 2999, или приблизительно 3000. Слева от точки пересечения MP(n + 1) > MS(n), то есть группа в целом выиграет от перехода еще одного человека на автомагистраль. Справа от точки пересечения все наоборот, то есть группа выиграет от перехода одного человека с автомагистрали на местные дороги. Таким образом, социально оптимальное распределение водителей — 3000 на автомагистрали и 3000 на местных дорогах.
При использовании подхода, основанного на дифференциальном исчислении, общий выигрыш водителей, передвигающихся по автомагистрали, можно было бы записать так: nP(n) = n(45 – 0,005n) = 45n – 0,005n2. Тогда MP(n + 1) — производная этого выражения по n, а именно 45 – 0,005 × 2n = 45 – 0,01n. Оставшая часть анализа выполняется так же, как описано выше.
Как обеспечить оптимальное распределение водителей с точки зрения общества в целом? В разных культурах и политических группах используются различные системы, каждая со своими преимуществами и недостатками. Общество может просто запретить 3000 водителям доступ на скоростную автомагистраль. Но по каким критериям их отбирать? Можно применить принцип живой очереди, но тогда водители будут пытаться обогнать друг друга, чтобы добраться до автомагистрали первыми, и потеряют кучу времени. Бюрократическое общество могло бы установить критерии, основанные на выполненных чиновниками сложных расчетах потребностей и заслуг, и тогда каждый водитель стал бы предпринимать затратные действия, чтобы удовлетворять этим критериям. Политизированное общество может отдать предпочтение важным «независимым избирателям», или организованным группам активистов, или лицам, делающим пожертвования. В коррумпированном обществе привилегии могли бы получить те, кто дает взятки чиновникам или политикам. Более эгалитарное общество может разыгрывать права на поездку по автомагистрали в лотерею или распределять их по ротационному принципу, каждый месяц меняя тех, кому они принадлежат. В качестве примера такого распределения можно привести схему, согласно которой вы получаете право ездить по автомагистрали только в определенные дни, в зависимости от последней цифры на номерном знаке вашего автомобиля. Однако такая схема не столь демократична, как может показаться поначалу, поскольку богатые люди могут купить два автомобиля и выбирать номерные знаки так, чтобы это позволяло им пользоваться автомагистралью ежедневно.
Многие экономисты предпочитают более открытую систему тарифов на проезд по автомагистрали. Предположим, каждый передвигающийся по ней водитель должен заплатить пошлину t, исчисляемую в единицах времени. В таком случае личная выгода от использования автомагистрали составляет P(n) – t, а число n в равновесии Нэша определяется выражением P(n) – t = S(n). (Здесь мы игнорируем малую разность между P(n) и P(n + 1), что допустимо при очень больших значениях N.) Мы знаем, что социально оптимальное значение n равно 3000. Воспользовавшись выражениями P(n) = 45 – 0,005n и S(n) = 15 и подставив 3000 вместо n, находим, что P(n) – t = S(n), то есть водителям безразлично, по какому маршруту ехать, автомагистралью или местными дорогами, если 45 – 15 – t = 15 или t = 15. Если стоимость времени при минимальной оплате труда составляет около 5 долларов в час, 15 минут обойдутся в 1,25 доллара. Это и есть пошлина, или плата за проезд, введение которой позволит удерживать количество водителей, пользующихся автомагистралью, на социально оптимальном уровне.
Обратите внимание, что, когда 3000 водителей пользуются автомагистралью, добавление одного участника движения увеличивает время пребывания каждого водителя в пути на 0,005 минуты, то есть в сумме на 15 минут. Это и есть та пошлина, которую должен заплатить каждый водитель. Другими словами, он должен оплатить стоимость отрицательного сопутствующего воздействия, оказываемого им на остальных членов группы. Это наглядно демонстрирует каждому водителю дополнительные издержки, которые влекут за собой его действия, что, в свою очередь, побуждает его выбрать социально оптимальное действие. Экономисты в таком случае говорят, что отдельный человек вынужден перенять экстерналию. Тот факт, что люди, действия которых причиняют вред другим людям, должны его оплачивать, повышает привлекательность данного подхода. Однако средства, вырученные от взимания пошлины, не передаются непосредственно на возмещение ущерба другим людям. Если бы это было так, то каждый пользователь автомагистрали рассчитывал бы получить за счет других именно ту сумму, которую он платит сам, и вся система потеряла бы смысл. Вместо этого деньги, вырученные от пошлины, уходят в казну государства, где их могут потратить (или не потратить) на благо общества.
Экономисты, предпочитающие полагаться на рынки, утверждают, что если бы автомагистраль находилась в частной собственности, ее владелец был бы заинтересован взимать такую плату за проезд, которая бы сократила количество пользователей автомагистрали до социально оптимального уровня. Владелец автомагистрали знает, что, если он взимает пошлину t с каждого водителя, их количество будет определяться по формуле P(n) – t = S(n). Его доход составит tn = n[P(n) – S(n)], и он будет действовать так, чтобы максимизировать его. В нашем примере доход равен n[45 – 0,005n – 15] = n[30 – 0,005n] = 30n – 0,005n2. Очевидно, что доход достигает максимума при n = 3000. Однако в этом случае прибыль уйдет в карман владельца автомагистрали, а большинство людей считают это неприемлемым.
Г. Положительные сопутствующие эффекты
Многие вопросы, касающиеся положительных сопутствующих эффектов, или положительных экстерналий, можно рассматривать как зеркальное отображение вопросов, связанных с отрицательными сопутствующими эффектами. Личная выгода человека от выполнения действий, обусловливающих положительный сопутствующий эффект, меньше маржинальной выгоды общества от этих действий. Следовательно, в случае равновесия Нэша такие действия будут применяться не очень активно и общество не получит от них адекватной выгоды. Более благоприятного результата можно достичь путем повышения заинтересованности людей; социальный оптимум можно обеспечить, предоставляя тем, чьи действия создают положительные сопутствующие эффекты, вознаграждение, эквивалентное выгоде от сопутствующего эффекта.
На самом деле различие между положительным и отрицательным сопутствующим эффектом — в какой-то мере вопрос семантики. Будет ли эффект положительным или отрицательным, зависит от того, какое выбранное действие вы обозначите символом P, а какое — S. Предположим, что в примере с регулярными поездками на работу и обратно мы обозначили местные дороги как P, а автомагистраль как S. Тогда переход одного человека с S на P сократит время в пути остальных людей, выбравших S, а значит, это действие создаст для них положительный сопутствующий эффект. Можно рассмотреть еще один пример — вакцинацию против некоторых инфекционных болезней. Каждый человек, сделавший прививку, снижает как собственный риск подхватить болезнь (маржинальная личная выгода), так и риск окружающих заразиться ею от него (сопутствующий эффект). Если отсутствие прививки обозначить как действие S, то вакцинация создает положительный сопутствующий эффект, если — как действие P, то отказ от вакцинации создает отрицательный сопутствующий эффект. Это имеет свои последствия для разработки политики приведения действий отдельных людей в соответствие с социальным оптимумом. Общество может либо вознаграждать тех, кто проходит вакцинацию, либо налагать взыскание на тех, кто отказывается от нее.
Однако действиям, создающим положительный сопутствующий эффект, может быть присуще одно важное новое свойство, отличающее их от действий с отрицательным сопутствующим эффектом, а именно положительная обратная связь. Предположим, сопутствующий эффект от выбора вами действия P связан с увеличением выигрыша тех, кто также выбрал P. В таком случае ваш выбор повышает привлекательность этого действия (P) и может склонить других тоже его совершить, положив начало процессу, который завершится всеобщим выполнением этого действия. Напротив, если действие P выбирают очень немногие люди, то оно может быть настолько непривлекательным, что они и сами откажутся от него, что приведет к всеобщему выбору действия S. Другими словами, положительная обратная связь может привести к формированию множества равновесий Нэша; ниже мы проиллюстрируем эту ситуацию на примере из реальной жизни.
При покупке компьютера вам необходимо решить, на базе какой операционной системы — Windows или Linux (семейство Unix) — он должен работать, чтобы это было выгоднее для вас. Чем активнее растет количество пользователей Unix, тем целесообразнее покупать такой компьютер: в системе будет меньше ошибок, поскольку пользователи их обнаружат и устранят, к тому же будет доступно больше приложений, а также увеличится число специалистов, которые смогут вам помочь при возникновении проблем. Точно так же привлекательность компьютера на Windows будет повышаться по мере увеличения количества пользователей этой ОС. Кроме того, многие компьютерные фанаты убеждены, что операционная система Unix вне всякой конкуренции. Придерживаясь нейтральной позиции по этому вопросу, мы покажем, что произошло бы, если бы это было действительно так. Приведет ли индивидуальный выбор к получению наиболее благоприятного для всего общества результата?
Для отображения выигрышей от двух стратегий, Windows и Unix, отдельного покупателя мы используем такой же график, как на и . Как показано на рис. 11.11, выигрыши от стратегии Unix повышаются по мере увеличения количества ее пользователей, а выигрыши от стратегии Windows повышаются, когда число пользователей Unix падает (соответственно, растет количество пользователей Windows). Как уже было сказано, этот график построен с учетом того, что выигрыш пользователей Unix, когда все остальные члены общей совокупности также предпочитают Unix (в точке U), выше выигрыша пользователей Windows, когда все остальные члены общей совокупности также выбирают Windows (в точке W).
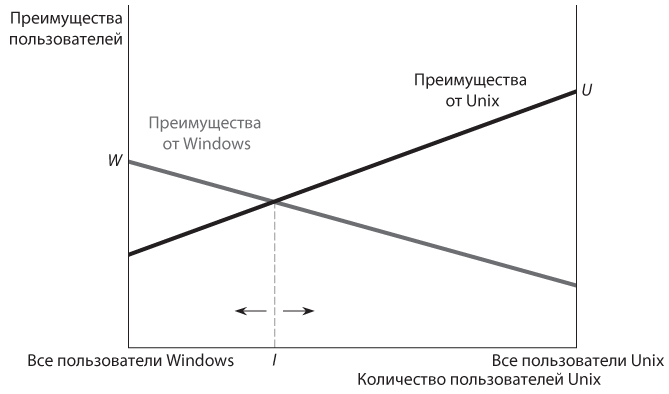
Рис. 11.11. Выигрыши в игре с выбором операционной системы
Если в текущей совокупности только небольшая доля пользователей Unix, то ситуация отображается на графике слева от точки пересечения линий выигрышей точкой I; при этом каждый отдельный пользователь считает более целесообразным выбрать Windows. Когда в общей совокупности доля пользователей Unix больше, это смещает всю совокупность направо от I и каждому пользователю лучше выбрать Unix. Таким образом, смешанная совокупность пользователей Unix и Windows может выступать в качестве равновесия только тогда, когда в текущей совокупности имеется ровно I пользователей Unix: лишь при этом условии ни у одного члена совокупности нет стимула перейти на другую платформу. Но даже эта ситуация неустойчива. Предположим, всего один человек случайно примет другое решение. Если он перейдет на Windows, его выбор сместит всю совокупность налево от точки I и тогда у других членов совокупности также появится стимул перейти на Windows. Если он перейдет на Unix, точка совокупности сместится направо от I, что стимулирует еще большее количество пользователей выбрать Unix. В конечном счете совокупный эффект этих переходов подтолкнет общую совокупность к исходу «все пользователи Unix» или «все пользователи Windows»; это и есть два устойчивых равновесия в данной игре.
Но какое из них будет достигнуто? Ответ зависит от того, где начинается игра. Если вы взглянете на конфигурацию современных пользователей компьютеров, то увидите среди них подавляющее большинство сторонников Windows. В связи с этим создается впечатление, что, поскольку пользователей Unix мало (или много пользователей Windows), мир движется к равновесию «все пользователи Windows». Школы, компании и частные пользователи оказались замкнутыми на этом равновесии вследствие исторической случайности. Если Unix действительно обеспечивает обществу дополнительные преимущества в случае ее повсеместного использования, тогда равновесие «все пользователи Unix» должно быть предпочтительнее по сравнению с равновесием «все пользователи Windows», к которому мы приближаемся. К сожалению, хотя общество в целом от такого изменения только бы выиграло, ни у одного пользователя компьютера нет личной заинтересованности менять сложившуюся ситуацию. Изменить ее в пользу Unix может только скоординированное действие. Прежде чем все посчитают целесообразным выбрать Unix, должна сформироваться критическая масса ее отдельных пользователей, превышающая имеющуюся в точке I на .
Существует много примеров подобного рода условностей, соблюдаемых различными группами людей. Наиболее известны случаи, в отношении которых по прошествии времени заговорили как об ошибочном выборе. Сторонники этой точки зрения заявляют, что паровые двигатели можно было бы сделать гораздо эффективнее, чем двигатели внутреннего сгорания, и уж конечно, они были бы более экологически чистыми. Приверженцы клавиатуры с раскладкой Дворака уверены, что она была бы лучше раскладки QWERTY, если бы применялась повсюду. Многие инженеры сходятся во мнении, что у Betamax было преимущество перед VHS на рынке видеомагнитофонов. В таких случаях пристрастие публики или талант рекламистов помогают определить окончательное равновесие и могут привести к «плохому» или «неправильному» исходу с точки зрения общества. В других ситуациях подобных трудностей нет. Например, мало кто стал бы бороться за изменение цвета огней светофора.
Идеи положительной обратной связи и замыкания нашли важное практическое применение в макроэкономике. Рентабельность производства возрастает по мере повышения уровня спроса в экономке, что происходит при увеличении национального дохода. А национальный доход, в свою очередь, увеличивается в связи с ростом выпуска продукции и, как следствие, рабочих мест. Такая положительная обратная связь позволяет сформировать множество равновесий, среди которых равновесие, включающее высокий объем производства и высокий национальный доход, гораздо лучше для общества, но отдельные решения могут замкнуть экономику на равновесии с низким объемом производства и низким национальным доходом. Более благоприятное равновесие можно сделать фокальной точкой, публично об этом заявив («Единственное, чего мы должны бояться, — это самого страха»). Кроме того, правительство могло бы также повысить спрос в экономике до уровня, необходимого для ее перевода в более выигрышное равновесие. Иными словами, с точки зрения теории игр вероятность безработицы из-за дефицита совокупного спроса (о чем в терминах спроса и предложения на языке экономической теории говорит Джон Кейнс в опубликованной в 1936 году книге под названием Employment, Interest, and Money) можно считать следствием неспособности решить проблему коллективного действия.
4. Краткая история идей
А. Классика
Проблема коллективного действия заботила социальных философов и экономистов с давних времен. Британский философ XVII столетия Томас Гоббс утверждал, что общество разрушится в «войне всех против всех», если не будет под властью монарха-диктатора, или Левиафана (название книги Гоббса). Сто лет спустя французский философ Жан-Жак Руссо описал проблему дилеммы заключенных в трактате «Рассуждение о начале и основании неравенства между людьми». Охота на оленя требует сотрудничества всей группы охотников с тем, чтобы они могли окружить и убить животное, но любой отдельно взятый охотник, увидевший зайца, может посчитать это более приемлемым вариантом для себя, покинуть круг и погнаться за зайцем. Руссо полагал, что такие проблемы — продукт цивилизации и что в своем естественном состоянии люди ведут гармоничную жизнь как «благородные дикари». Примерно в то же время два шотландца сформулировали ряд кардинальных решений подобных проблем. Давид Юм в своем труде «Трактат о человеческой природе» утверждал, что ожидание ответной услуги в будущем обеспечивает взаимодействие между людьми. Адам Смит в работе «Исследование о природе и причинах богатства народов» сформулировал важное видение экономики, согласно которому производство товаров и услуг сугубо в целях получения личной прибыли может привести к наилучшему исходу для общества в целом.
Столь оптимистическая интерпретация настолько укрепила свои позиции (особенно среди экономистов и даже некоторых политологов), что автоматически предполагалось следующее: если тот или иной результат приносит выгоду всей группе, действия ее членов обязательно приведут к его получению. Это убеждение было подвергнуто резкой критике в середине 1960-х годов, после выхода книги Манкура Олсона «Логика коллективного действия». Олсон отметил, что наилучший коллективный результат не будет достигнут, если каждый отдельно взятый человек не будет лично в этом заинтересован, то есть если не сформируется равновесие Нэша. Однако Олсон не конкретизировал игру с коллективным действием. Хотя у нее много общего с дилеммой заключенных, Олсон настаивал, что это не всегда так, и мы с вами уже убедились, что данная проблема может принимать форму игры в труса или игры в доверие.
Примерно в то же время внимание ученых привлек еще один важный класс проблем коллективного действия, а именно проблемы исчерпания общих ресурсов. Если доступ к таким ресурсам, как рыбные запасы или пастбища, открыт для всех, каждый человек будет эксплуатировать их по максимуму, поскольку любое самоограничение с его стороны просто приведет к тому, что это будет делать кто-то другой. Как уже упоминалось выше, Гаррет Хардин написал по этой теме знаменитую статью под названием «Трагедия общин». Проблемы совместно используемых ресурсов отличаются от игры со строительством оросительной системы, в которой у каждого фермера есть сильный личный стимул бесплатно воспользоваться результатами труда других людей. Что касается общих ресурсов, то здесь каждый человек лично заинтересован извлечь из них максимальную выгоду, заставив остальных оплачивать социальные издержки в связи с их истощением.
Б. Современные подходы и решения
До недавнего времени многие социологи и большинство специалистов по естественным наукам придерживались точки зрения Гоббса на проблему общих ресурсов, заявляя, что ее способно решить только правительство, которое заставит всех поддерживать взаимодействие. Другие, особенно экономисты, сохранили оптимизм Смита. Они утверждали, что передача ресурса в частную собственность, при которой выгода от него будет выражена в виде прибыли владельца, побудит его ограничить использование ресурса, обеспечив тем самым социальный оптимум. Владелец поймет, что в будущем ценность ресурса (например, рыбы или травы) повысится в связи с его уменьшением, а значит, он сможет получить больше прибыли, сохранив часть ресурса.
В настоящее время специалисты из самых разных областей осознали, что проблемы коллективного действия принимают всевозможные формы и что не существует универсального способа справиться с ними. Кроме того, они пришли к выводу, что группы или общества не остаются беспомощными перед лицом таких проблем, а изобретают разные варианты их решения. Большая часть работ по этой теме основана на анализе повторяющихся дилемм заключенных и других подобных игр с точки зрения теории игр.
Решения проблем коллективного действия всех типов должны побуждать отдельных членов группы действовать сообща или таким образом, чтобы это приносило ей максимальную пользу, даже если не отвечает интересам человека. Например, обмен подарками и навыки обнаружения обмана настолько типичны для всех обществ и всех времен, что есть все основания утверждать, что это может происходить на инстинктивном уровне. Однако человеческое общество в значительной мере полагается на специальные социальные и культурные традиции, нормы и санкции в целях стимулирования кооперативного поведения отдельных членов общества. Эти методы представляют собой осознанные, продуманные попытки разработать игру для решения проблемы коллективного действия. Мы подходим к вопросу поиска методов решения с учетом такого фактора, как тип игры.
Решить проблему коллективного действия легче всего, если она принимает форму игры в доверие. Тогда каждый человек лично заинтересован в совершении наилучшего в социальном плане действия, если рассчитывает на то, что все остальные поступят так же. Другими словами, социально оптимальный исход — это равновесие Нэша. Единственная проблема, что в той же игре существуют и другие равновесия Нэша, менее выигрышные в социальном плане. В таком случае все, что необходимо для достижения наилучшего равновесия Нэша, а значит, и социального оптимума, — сделать такой исход фокальной точкой, то есть обеспечить на нем сходимость ожиданий игроков. Такая сходимость может проистекать из социальной традиции, или соглашения, а именно линии поведения, которая принимается автоматически, поскольку каждый человек заинтересован ее придерживаться, если предполагается, что остальные тоже должны это делать. Например, если фермеры, пастухи, ткачи и другие производители в том или ином регионе хотят собираться и торговать своей продукцией, все, что им нужно, — это уверенность в том, что у них будет с кем торговать. Тогда традиция еженедельно проводить ярмарку в деревне X в день Y делает присутствие в этом месте в это время оптимальным для всех.
Но остается одна сложность. Для того чтобы желаемый результат стал фокальной точкой, каждый человек должен быть уверен в том, что остальные понимают это, что, в свою очередь, требует, чтобы они были уверены в том, что все остальные понимают это… Иными словами, фокальная точка должна быть общим знанием. Как правило, для этого необходимо заранее предпринять определенное социальное действие. Скажем, это может быть публикация в одном из средств массовой информации с широким кругом читателей или обсуждение с сидящими по кругу людьми, чтобы каждый мог убедиться, что остальные внимательно слушают.
Представленный в анализ позволяет предположить, что отдельные выигрыши во многих случаях имеют конфигурацию, при которой проблемы коллективного действия, особенно в крупных группах, принимают форму дилеммы заключенных. Неудивительно, что методы решения таких проблем удостоились самого пристального внимания.
Самый простой метод — изменить предпочтения игроков так, чтобы игра перестала быть дилеммой заключенных. Если отдельные люди получают удовольствие от сотрудничества или испытывают чувство вины или стыда, когда обманывают, они будут сотрудничать, чтобы максимизировать свои выигрыши. Если дополнительный выигрыш от сотрудничества зависит от определенных условий (человеку нравится взаимодействовать с другими или он испытывает чувство вины или стыда, прибегая к обману, если и только если другие сотрудничают), то игра может превратиться в игру в доверие. В одном из ее равновесий каждый игрок идет на сотрудничество, потому что большинство тоже делают это, а в другом никто не взаимодействует, поскольку никто этого не делает. В таком случае проблема коллективного действия упрощается и сводится к тому, чтобы сделать более благоприятное равновесие фокальной точкой. Если дополнительный выигрыш от сотрудничества не зависит ни от каких условий (человеку нравится взаимодействовать с другими или он испытывает чувство вины или стыда, прибегая к обману, независимо от того, что делают другие), тогда в этой игре может быть единственное равновесие, при котором все игроки поддерживают сотрудничество друг с другом. Во многих ситуациях даже необязательно, чтобы такой дополнительный выигрыш получали все без исключения. Если его получает довольно приличная часть общей совокупности игроков, этого может быть достаточно для достижения требуемого результата.
Некоторые из таких просоциальных предпочтений бывают врожденными, заложенными в человека в ходе биологической эволюции. Однако чаще они становятся продуктом социального или культурного развития. В большинстве обществ предпринимаются намеренные усилия, чтобы развить у детей просоциальное мышление в процессе социализации в семьях и школах. Усиление таких предпочтений наблюдается в ходе экспериментов с ультимативными и диктаторскими играми, о которых шла речь в . Когда подобные эксперименты проводятся с детьми разного возраста, самые маленькие дети ведут себя эгоистично. Однако к восьми годам у них развивается достаточно сильное чувство равенства. После этого у детей формируются истинные просоциальные предпочтения (хотя время от времени они демонстрируют эгоистичное поведение) и наконец чувство справедливости, свойственное взрослому человеку. Таким образом, на протяжении длительного процесса обучения и накопления опыта общепринятые нормы постепенно внедряются в предпочтения людей.
Тем не менее у разных людей может быть разная степень принятия просоциальных предпочтений, и этого может оказаться недостаточно для решения проблем коллективного действия. Многие люди имеют весьма широкое представление о том, что такое социально кооперативное действие в большинстве ситуаций, однако отдельные люди подвержены соблазну пойти на обман. Следовательно, для обеспечения кооперативных действий необходима система внешних санкций или мер наказания. Мы называем правила поведения, которые находят широкое понимание, но не выполняются автоматически, принудительными нормами.
В мы подробно описали несколько методов достижения кооперативного исхода в играх категории «дилемма заключенных», в том числе повторение, взыскание (или вознаграждение) и лидерство. Тогда нас главным образом интересовали примеры дилеммы заключенных с двумя участниками. Эти методы (с некоторыми коррективами) применимы и для принудительного выполнения норм в случае проблем коллективного действия в больших группах.
Как мы подчеркивали в , повторение — самый важный из методов, поэтому мы уделим ему повышенное внимание. Повторение позволяет достичь кооперативного исхода в качестве равновесия действий отдельных игроков в повторяющейся дилемме заключенных посредством создания перспективы того, что обман приведет к прекращению сотрудничества. В более общем плане все, что необходимо для поддержания сотрудничества, — это осознание каждым игроком того, что его личные выигрыши от обмана преходящи и что их место быстро займет более низкий выигрыш по сравнению с тем, что игрок мог бы получить в случае кооперативного поведения. Для того чтобы игроки понимали, что обман им невыгоден в долгосрочной перспективе, он должен быть быстро обнаружен, а последующее наказание (уменьшение будущих выигрышей) — эффективно, неминуемо и болезненно.
В этом отношении у группы есть одно важное преимущество перед парой отдельных людей. У двух человек может и не быть повода часто общаться, но каждый из них, по всей вероятности, будет постоянно взаимодействовать с кем-то из группы. Следовательно, искушение игрока Б обмануть игрока А может подавить страх того, что другие игроки, например В, Г и т. д., с которыми он встретится в будущем, накажут его за это. Экстремальную ситуацию, в которой двустороннее взаимодействие не повторяется, а наказание должна осуществить от чьего-то имени третья сторона, можно описать словами Йоги Берра: «Всегда ходите на похороны других, иначе они не придут на ваши».
Однако у группы, когда речь заходит о поддержании хорошего поведения в ходе повторяющегося взаимодействия, есть ряд недостатков по сравнению с прямым двусторонним контактом. Требуемая скорость и безошибочность обнаружения обмана и наказания мошенников снижается по мере увеличения численности группы. В небольших деревенских общинах можно наблюдать массу примеров успешного сотрудничества, которое было бы немыслимым в большом городе или в штате.
Для начала поговорим о выявлении обмана, что всегда непросто. В большинстве реальных ситуаций выигрыши зависят не только от действий игроков, но и от тех или иных случайных флуктуаций. Даже в игре с двумя участниками один игрок, получив низкий выигрыш, не может быть уверен, что другой его обманул: это могло быть следствием какого-либо случайного события. По мере увеличения количества игроков возникает дополнительный вопрос: если кто-то и обманул, то кто именно? Наказывать кого-то без веских оснований и уверенности в том, что этот человек действительно виновен, не только аморально, но и контрпродуктивно. Мотивация к сотрудничеству ослабевает, если даже кооперативные действия могут по ошибке повлечь за собой наказание.
Кроме того, в играх с большим количеством участников, даже если обман обнаружен и известно, кто на него пошел, об этом необходимо быстро и точно сообщить другим игрокам. Для этого группа должна быть достаточно маленькой либо иметь эффективную сеть коммуникации или распространения слухов. К тому же у игроков не должно быть причин выдвигать против кого-то ложные обвинения.
И наконец, даже после выявления обмана и информирования об этом всех членов группы необходимо как-то наказать обманщика (принудительное выполнение социальной нормы). Зачастую третьей стороне приходится нести определенные личные издержки в связи с осуществлением наказания. Например, если игроку В поручено наказать игрока Б, обманувшего игрока А, то игроку В, возможно, придется пожертвовать прибыльной сделкой, которую он планировал заключить с игроком Б. В таком случае применение наказания само по себе становится игрой с коллективным действием и наличием искушения «уклониться» от исполнения наказания. Общество могло бы организовать второй круг наказаний за уклонение, но это, в свою очередь, обусловит еще одну проблему коллективного действия! Тем не менее создается впечатление, что у людей сформировался инстинкт, благодаря которому они получают личное удовлетворение от наказания обманщиков, даже если сами не являются их жертвами. Интересно, что принцип «даже несмотря на высокие личные издержки, необходимо ввести санкции по отношению к нарушителям принудительных социальных норм», по всей вероятности, сам стал общепринятой нормой.
Действие норм усиливается, когда подавляющее большинство членов общества их придерживается, и теряет силу, если они часто нарушаются. До появления государства всеобщего благосостояния, когда люди, столкнувшись со сложными экономическими временами, вынуждены были полагаться исключительно на помощь семьи, друзей и ближайших членов малой социальной группы, трудовая этика представляла собой норму, сдерживающую соблазн ослабить собственные усилия и незаслуженно пользоваться поддержкой окружающих. Но как только государство взяло на себя обязательства по обеспечению поддержки и выплаты пособий по безработице, то есть когда предоставление социальной помощи стало обязательным, эта норма трудовой этики утратила силу. После резкого повышения уровня безработицы в Европе в конце 1980-х — начале 1990-х годов значительная доля населения воспользовалась официальной системой социальной поддержки, после чего эта норма ослабла еще больше.
В разных обществах и культурных группах могут сформироваться разные соглашения и нормы, направленные на достижение одной и той же цели. На бытовом уровне в каждой культуре есть свой набор хороших манер, таких как приветствие незнакомых людей, выражение благодарности за угощение и т. д. При встрече представителей разных культур между ними могут возникнуть недоразумения. Не менее важно, что в каждой компании или офисе придерживаются своих подходов. Хотя различия между традициями и нормами едва уловимы, многие слияния потерпели неудачу именно из-за конфликта корпоративных культур.
Далее рассмотрим коллективные игры в виде игры в труса. Здесь характер способа решения проблемы коллективного действия зависит от того, будет ли получен максимальный социальный выигрыш, если каждый член группы примет участие в совершении соответствующего действия (в эта игра обозначена как версия I игры в труса) или если кто-то сотрудничает, а кому-то можно отказаться от него (версия II игры в труса). В первой версии игры в труса, в которой каждый игрок заинтересован уклониться от выполнения действия, проблема очень напоминает проблему поддержания сотрудничества в дилемме заключенных, поэтому все приведенные выше комментарии в ее отношении применимы и к этой игре. Вторая версия игры в труса отличается: в чем-то она легче, а в чем-то сложнее. После распределения ролей между участниками и уклонистами ни у кого нет личного стимула сменить стратегию: если другому водителю поручена роль «ехать прямо», то вам лучше свернуть, и наоборот. Следовательно, если в силу традиции необходимо достичь равновесия, его можно обеспечить без дальнейшего социального вмешательства, например, в виде санкций. Но при таком равновесии игроки, уклоняющиеся от совершения действия, получают более высокие выигрыши, чем выполняющие его. Подобное неравенство способно создать проблемы в данной игре: серьезные конфликты и противоречия могут поставить под угрозу саму структуру общества. Часто такая проблема решается посредством повторения. Роли тех, кто участвует в совершении действия, и тех, кто уклоняется от них, можно поочередно менять, чтобы уравновесить выигрыши в долгосрочной перспективе.
Иногда проблема дифференцированных выигрышей во второй версии дилеммы заключенных или игры в труса «решается» не путем восстановления равенства, а посредством притеснения или принуждения, когда доминируемая подгруппа общества вынуждена принять более низкий выигрыш, тогда как доминирующая подгруппа получает более высокий выигрыш. На протяжении всей истории человечества во многих обществах работу по разделке туш животных в принудительном порядке поручали определенным подгруппам или кастам. Наглядный пример этой практики — дискриминация расовых и этнических меньшинств или женщин. Как только устанавливается такая система, ни один член притесняемой группы не может ничего сделать, чтобы повлиять на ситуацию. Угнетенные должны объединить усилия и действовать как единая группа, чтобы изменить всю систему, что само по себе представляет еще одну проблему коллективного действия.
И наконец, рассмотрим роль лидерства в решении проблем коллективного действия. В мы отмечали, что, если в игре участвуют игроки разного масштаба, дилемма заключенных может исчезнуть сама по себе, поскольку более крупный игрок может быть заинтересован в продолжении сотрудничества и по этой причине примет обман более мелкого игрока. Здесь же мы отдаем должное другому типу величия — величию сердца. Хотя у людей в большинстве групп разные предпочтения, во многих группах есть один или несколько человек, получающих истинное удовлетворение от личного вклада в благополучие всей группы. Если таких людей достаточно для выполнения текущей задачи, то проблема коллективного действия исчезает. Большинство школ, церквей, местных больниц и других важных для общества учреждений полагаются на работу волонтеров. Это решение, как и многие другие, более эффективно в небольших группах, где результаты действий их членов непосредственно видны их благодетелям, которые заинтересованы в умножении добрых дел.
В. Практическое применение
В книге «Управляя общим» Элинор Остром приводит ряд примеров решения проблем общих ресурсов на местном уровне. Большинство из них предполагают использование особенностей конкретной ситуации для создания системы обнаружения проблем и наказания виновных. Например, между членами одной рыбацкой общины на побережье Турции применяется такой метод, как ротация участков для вылова рыбы. Человек, получивший разрешение ловить рыбу на определенном участке, сразу же заметит и сообщит о нарушителе, который попытается рыбачить на том же участке. Многие другие пользователи ресурсов, находящихся в общей собственности, в том числе общинных пастбищ в средневековой Англии, на самом деле ограничивали к ним доступ и боролись с их чрезмерной эксплуатацией, предоставляя сложные, негласные, но вполне понятные права отдельным людям. В каком-то смысле такое решение позволяет обойти проблему общих ресурсов, разделив ресурс на несколько более мелких единиц, находящихся в частной собственности.
Самая поразительная особенность примеров Остром — их огромное разнообразие. Одни дилеммы заключенных, касающиеся использования общих ресурсов, которые изучала Остром, были решены посредством частной инициативы группы людей, вовлеченных в соответствующую дилемму; другие — путем внешнего вмешательства со стороны общественности или правительства. Иногда дилемма не решалась вообще и группа оставалась в ловушке исхода, при котором все ее члены предпочитали уклониться от решения проблемы. Тем не менее, несмотря на кажущееся разнообразие, Остром выделяет ряд общих характеристик, облегчающих проблему решения дилемм заключенных в контексте коллективного действия: 1) обязательно наличие поддающейся идентификации и стабильной группы потенциальных участников; 2) преимущества сотрудничества должны быть достаточно заманчивыми, чтобы это могло покрыть все затраты на мониторинг и принудительное соблюдение правил сотрудничества; 3) важно, чтобы члены группы могли взаимодействовать друг с другом. Последнее условие обеспечивает достижение нескольких целей. Во-первых, такая коммуникация помогает установить четкие нормы: все знают, какого поведения от них ожидают, какой обман недопустим и какие санкции будут применены по отношению к обманщикам. Кроме того, наличие коммуникации позволяет информировать об эффективности обнаружения механизма обмана, что способствует росту доверия между членами группы и устранению любых подозрений любого участника, если он считает, что придерживается установленных правил, тогда как другие их безнаказанно нарушают. И последнее: коммуникация между членами группы позволяет им отслеживать эффективность действующих договоренностей и по мере необходимости улучшать их. Все эти требования поразительно напоминают выводы, сделанные нами в на основании теоретического анализа дилеммы заключенных и информации о турнирах Аксельрода.
Изучение Остром жизни рыбацкой деревни также помогло понять, что можно предпринять, если коллективный оптимум требует, чтобы разные люди выполняли разные действия, с учетом того, что при этом одни будут получать более высокий выигрыш, чем другие. В случае повторяющегося взаимодействия можно организовать ротацию более выгодной позиции среди участников, тем самым гарантируя определенное чувство равенства в долгосрочной перспективе.
По мнению Остром, внешняя сторона, обеспечивающая выполнение установленных правил, не в состоянии достаточно четко и оперативно выявить обман и применить наказание. Поэтому типичная точка зрения, согласно которой для решения проблем коллективного действия необходима централизованная или государственная политика, часто оказывается ошибочной. Еще один пример — сельские общины, или «коммуны», в России конца XIX столетия. Этим коммунам удалось решить многие проблемы коллективного действия в сфере ирригации, севооборота, управления использованием лесов и пастбищ, а также строительства и ремонта дорог и мостов. «Деревня… не была раем в плане общинной гармонии. …Просто коллективная деятельность во многих случаях отвечала личным интересам отдельных крестьян». Реформаторы царского правительства начала XX века, так же как и советские революционеры 1920-х годов, потерпели неудачу не только потому, что старая система настолько овладела умами крестьян, что они сопротивлялись всему новому, но еще и потому, что реформаторы не смогли понять роль некоторых широко распространенных практик в решении проблем коллективного действия, а потому и не сумели заменить их равноценными альтернативами.
Различия между маленькими и большими группами хорошо проиллюстрировал Авнер Грейф, сравнивший две группы торговцев в странах средиземноморского бассейна в средневековые времена. Магрибские торговцы представляли собой группу еврейских купцов, которые полагались на большую семью и прочные социальные связи. Если один член группы обманывал другого, жертва обмана сообщала об этом остальным, рассылая письма. При наличии веских доказательств вины больше ни один член группы не вел дел с обманщиком. Система была прекрасно налажена и хорошо работала в случае мелкой торговли. Но когда торговля распространилась по всем странам Средиземноморья, система коллективного контроля помешала дальнейшему развитию магрибской торговли: группа не смогла найти достаточно близких или надежных доверенных лиц, чтобы использовать в этих странах новые торговые возможности.
Напротив, генуэзские торговцы создали более официальную правовую систему. Любой контракт необходимо было регистрировать в центральных органах власти в Генуе. Тот, кто становился жертвой обмана или нарушения контракта, должен был направить жалобу в органы власти, которые проводили расследование и взимали с обманщиков надлежащие штрафы. Эту систему, при всех ее проблемах с обнаружением обмана, можно было без труда модифицировать в случае расширения торговли. По мере роста экономики и мировой торговли мы наблюдаем аналогичный переход от сплоченных групп к более отстраненным торговым отношениям и от обеспечения выполнения правил на основании повторяющегося взаимодействия к применению официального законодательства.
Идея о том, что небольшие группы более эффективно решают проблемы коллективного действия, стала основной темой книги Манкура Олсона The Logic of Collective Action («Логика коллективного действия») и позволила сделать одно важное наблюдение в политологии. В демократическом обществе все избиратели имеют равные политические права, поэтому предпочтения большинства должны доминировать. Однако известно немало случаев, когда этого не происходит. Как правило, та или иная политика имеет положительные последствия для одних групп и отрицательные для других. Для того чтобы добиться принятия предпочтительной для себя политики, группа должна предпринять определенные политические действия, такие как лоббирование, распространение информации, пожертвования на ведение избирательной кампании и т. д. Но для этого группа должна решить проблему коллективного действия, поскольку каждый ее член может попытаться уклониться и извлечь для себя выгоду из действий других членов группы. Если небольшие группы лучше справляются с этой проблемой, то политический курс, проистекающий из политического процесса, будет отображать их предпочтения, даже несмотря на то что другие группы, которым не удалось создать организованную структуру, более многочисленны и терпят убытки, размер которых превышает прибыль успешных групп.
Наиболее яркий пример политических мер, отображающих предпочтения организованной группы, связан с торговой политикой. Действующие в стране ограничения на импорт помогают отечественным производителям, чьи товары конкурируют с импортными, но ущемляют интересы потребителей обеих категорий товаров, поскольку цены на них выше, чем были бы в случае отсутствия ограничений на импорт. Отечественных производителей немного, а потребители — почти все население, и, как правило, общая сумма их убытков гораздо больше общего объема прибыли производителей. Политические соображения, основанные на численности электората, и экономические соображения, такие как прибыли и убытки, позволяют рассчитывать на победу потребителей на этой политической арене или хотя бы на какую-то поддержку идеи о том, что ограничения на импорт следует отменить, однако этого не происходит. Более мелкие и сплоченные ассоциации производителей могут лучше организовать выполнение политического действия, чем многочисленные, но разрозненные потребители.
Более 70 лет назад американский политолог Элмер Шаттшнайдер впервые представил подробное документальное подтверждение и анализ влияния политического давления на торговую политику. Он признал тот факт, что «способность группы к самоорганизации существенно сказывается на ее деятельности», но не разработал системную теорию того, что именно определяет такую способность. Анализ Олсона и других исследователей улучшил наше понимание этого вопроса, однако триумф политического давления над экономикой продолжается в торговой политике до сих пор. Например, в конце 1980-х годов политика США в области производства сахара обошлась каждому из 240 миллионов жителей страны в 11,5 доллара в год, что в общей сложности составило 2,75 миллиарда долларов; при этом доход около 10 000 фермеров, выращивающих сахарную свеклу, увеличился на 500 000 долларов в расчете на одного фермера, или в целом на 1 миллиард долларов. Чистый убыток американской экономики составил 1,75 миллиарда долларов. Каждый неорганизованный потребитель продолжает молча нести свою небольшую долю издержек; многие даже не осознают, что платят за свое пристрастие к сладкому на 11,5 доллара в год больше.
Если наш обзор теории и практики решения проблем коллективного действия кажется вам слишком разноплановым и не содержащим четкого краткого описания сути происходящего, то это потому, что сами проблемы столь же разнообразны и решение каждой из них зависит от ее специфики. Единственный общий вывод, который мы можем сделать, касается понимания того, насколько важно предоставить право самим участникам коллективного действия найти решение, воспользовавшись локальным знанием ситуации, возможностью мониторинга действий других членов общества, направленных на сотрудничество или уклонение от него, а также шансом применить санкции к уклоняющимся посредством различных вариантов непрерывного взаимодействия в рамках данной социальной группы.
В заключение хотелось бы высказать одно предостережение. Возможно, после обсуждения проблем коллективного действия у вас появится ощущение, что личная свобода неизменно приводит к пагубным результатам, которые можно и нужно исправлять с учетом социальных норм и санкций. Но не стоит забывать, что, кроме проблем коллективного действия, общество сталкивается и с другими проблемами, причем некоторые из них лучше решать посредством личной инициативы, а не совместных усилий. Общество может быть слишком консервативным и автократическим, оказавшись в ловушке своих норм и традиций и подавляя инновации, которые зачастую становятся ключом к экономическому росту. Коллективное действие может стать коллективным бездействием.
5. «Помогите!»: игра в труса со смешанными стратегиями
В ходе анализа проблем с коллективным действием в контексте игры в труса мы рассматривали только равновесия в чистых стратегиях. Однако из мы знаем, что в таких играх есть также равновесия в смешанных стратегиях. В задачах с коллективным действием каждый участник думает: «Мне лучше подождать, пока наберется достаточное количество желающих поучаствовать, тогда я мог бы уклониться от этого; хотя, опять же, они тоже могут отказаться, и тогда мне придется вмешаться». Смешанные стратегии прекрасно отображают характер подобных колебаний. Наша последняя история — весьма драматичный, возможно, даже жуткий пример применения такого равновесия в смешанных стратегиях.
В 1964 году в Нью-Йорке (в районе Кью-Гарденс, Квинс) в результате зверского нападения, длившегося более получаса, была убита женщина по имени Китти Дженовезе. Все это время она кричала, но, несмотря на то что многие слышали ее крики, а три человека даже были свидетелями происходящего, никто не поспешил ей на помощь и даже не вызвал полицию.
История произвела сенсацию, и сразу же нашлось несколько теорий, объясняющих случившееся. Пресса и большая часть общественности увидели в этом случае подтверждение их убежденности в том, что ньюйоркцы (или жители мегаполисов, или американцы, или люди вообще) совершенно безразличны к судьбе ближнего.
Тем не менее даже небольшой самоанализ или наблюдение убедят вас в том, что люди заботятся о благополучии других, даже незнакомых, людей. Социологи предложили иное объяснение произошедшего под названием плюралистическое неведение. В его основе лежит следующая идея: никто не может быть уверен в том, что именно происходит, действительно ли нужна помощь и в каком объеме. Люди смотрят друг на друга в поисках подсказок или советов по таким вопросам и в этом свете пытаются интерпретировать поведение окружающих. Если они видят, что никто ничего не предпринимает, они делают вывод, что помощь, скорее всего, не нужна, и по этой причине тоже самоустраняются. Это объяснение обладает определенной интуитивной привлекательностью, но неубедительно в случае Китти Дженовезе. Можно с высокой степенью уверенности предположить, что кричащей женщине нужна помощь. Что думали при этом очевидцы? Что в их мрачном районе снимают кино? Если да, то где прожекторы, камеры, режиссер и прочие члены съемочной группы?
Более подходящее объяснение сводилось бы к тому, что, хотя каждый очевидец пережил настоящий шок от увиденного и получил бы истинное личное удовольствие, если бы Китти удалось спасти, он должен привести это в соответствие с издержками участия в происходящем. Ведь придется назвать свое имя, позвонив в полицию, затем выступить в суде в качестве свидетеля и т. д. Таким образом, мы видим, что каждый человек может решить, что ему лучше подождать, пока в полицию позвонит кто-то другой, в надежде на то, что сам он получит преимущество «безбилетника» в виде удовлетворенности в связи с успешным спасением жертвы.
У социальных психологов несколько иная версия идеи «безбилетника», которую они обозначают термином диффузия ответственности. Согласно ей все люди, вовлеченные в сложившуюся ситуацию, понимают, что помощь необходима, но поскольку не поддерживают прямых контактов друг с другом, не могут договориться о том, кто именно ее окажет. Каждый человек может считать, что ответственность за оказание помощи лежит на ком-то другом. Чем больше группа, тем выше вероятность того, что каждый человек понадеется, что поможет кто-то другой и это позволит ему оградить себя от возможных проблем и издержек в будущем.
Социальные психологи провели ряд экспериментов для проверки этой гипотезы. Они разыгрывали ситуации, в которых кому-то требовалась помощь разных типов, в разных местах, в присутствии разных групп людей. Среди прочего авторы экспериментов обнаружили, что чем больше толпа, тем меньше вероятность получить помощь.
Концепция диффузии ответственности объясняет этот вывод, но не до конца. Согласно ей, чем больше толпа, тем меньше вероятность того, что один человек поможет. Хотя из большого количества людей нужен всего один человек, который начал бы действовать, вызвал полицию и тем самым оказал помощь. Но чтобы снизилась вероятность того, что хотя бы один человек поможет, нужно, чтобы вероятность того, что любой человек поможет, снижалась достаточно быстро, чтобы компенсировать общее количество потенциальных помощников. Для того чтобы выяснить, действительно ли это так, понадобится анализ на основании теории игр, который мы проведем ниже.
Мы рассмотрим только один аспект диффузии ответственности, когда не происходит осознанная координация действий, и оставим в стороне остальные сложности в связи с информацией и выводом. Таким образом, мы будем исходить из следующего предположения: все считают, что помощь необходима и это стоит понесенных издержек.
Допустим, группа насчитывает N человек. Действие приносит каждому из них выгоду B. Для его совершения нужен всего один человек; большее количество будет избыточным. Любой, кто предпримет необходимое действие, понесет при этом издержки C. Мы исходим из того, что B > C, то есть любому члену группы стоит потратить какие-то усилия на совершение действия, даже если больше никто этого не сделает. Таким образом, необходимость выполнить действие абсолютно обоснованна.
Проблема в том, что любой, кто предпримет действие, получит выигрыш B, но понесет издержки C (то есть чистый выигрыш составит B – C), тогда как он получил бы более высокий выигрыш B, если бы это действие совершил кто-то другой. Следовательно, у каждого члена группы есть соблазн переложить задачу на кого-то другого, а самому воспользоваться преимуществами достигнутого в итоге результата. Каким будет равновесие или исход игры, если так рассуждают все N членов группы?
Если N = 1, то это не столько игра, сколько проблема принятия решения одним человеком. Он получит выигрыш B – C > 0, если выполнит необходимое действие, и выигрыш 0, если не сделает этого. Поэтому он решает помочь.
Если N > 1, мы имеем игру в стратегическое взаимодействие с несколькими равновесиями. Давайте начнем с исключения некоторых возможностей. При N > 1 не может быть равновесия Нэша в чистых стратегиях, при котором все члены группы совершают необходимое действие, поскольку тогда любому из них было бы выгоднее стать «безбилетником». Точно так же не может быть равновесия Нэша в чистых стратегиях, когда никто не совершает необходимого действия, так как при условии, что никто ничего не станет делать (вспомните, что, согласно предположению Нэша, каждый игрок воспринимает стратегии других игроков как факт), ни одному человеку нет смысла действовать.
Тем не менее равновесия Нэша, в которых действие предпримет в точности один человек, все же существуют; на самом деле есть ровно N таких равновесий, по одному на каждого члена группы. Однако, когда каждый человек принимает решение в индивидуальном порядке, отдельно от остальных, нет никакого способа договориться о том, кто именно совершит необходимое действие. Даже если бы члены группы предприняли попытку такой координации, они могли бы при обсуждении, кто несет ответственность за совершение действия, не прийти к единому мнению, во всяком случае пока еще остается время для оказания помощи. Следовательно, интерес представляет только анализ симметричных равновесий, в которых у всех членов группы одинаковые стратегии.
Мы уже видели, что не может быть равновесия, при котором все N членов группы придерживались бы одной и той же чистой стратегии. Значит, мы должны выяснить, возможно ли равновесие, при котором все они придерживались бы одной и той же смешанной стратегии. На самом деле смешанные стратегии весьма привлекательны в данном контексте. Члены группы изолированы друг от друга, и каждый пытается угадать, что будут делать другие. Каждый размышляет так: «Может, мне следует позвонить в полицию… но вдруг это сделает кто-то другой… а если никто этого не сделает?» Каждый член группы в какой-то момент прерывает эту цепочку рассуждений и делает последнее, о чем подумал, но у нас нет способа определить, что именно это будет. В смешанной стратегии также присутствует этот принцип цепочки догадок, которая прерывается в произвольный момент времени.
Итак, допустим, что P — это вероятность того, что любой из членов группы не станет предпринимать необходимое действие. Если один человек готов смешать стратегии, ему должно быть безразлично, какую именно из двух чистых стратегий выбрать — действовать или нет. Совершение действия гарантированно обеспечит ему выигрыш (B – C), а отказ — выигрыш 0, если ни один из оставшихся (N – 1) членов группы не станет действовать, и выигрыш B, если хотя бы один человек предпримет необходимое действие. Поскольку вероятность того, что любой из членов группы не станет действовать, равна P, и учитывая, что они принимают решения независимо друг от друга, вероятность того, что никто из оставшихся (N – 1) членов группы не станет действовать, составит PN – 1, а вероятность того, что хотя бы один человек выполнит необходимое действие, равна (1 – PN – 1). Следовательно, ожидаемый выигрыш одного человека в случае, если он не будет действовать, равен
0 × PN – 1 + B(1 – PN – 1) = B(1 – PN – 1).
И ему безразлично, предпримет он необходимое действие или нет, при таком условии:
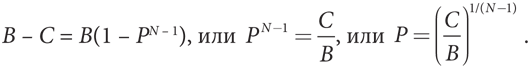
Обратите внимание, как условие безразличия одного отдельно взятого игрока определяет вероятность, с которой другие игроки будут смешивать свои стратегии.
Получив вероятность равновесной комбинации стратегий, мы теперь можем проанализировать, как она меняется по мере изменения численности группы N. Помните, что C/B < 1. По мере увеличения N от 2 до бесконечности степень 1/(N – 1) снижается от 1 до 0. В таком случае C/B, взятое в этой степени (то есть P), увеличивается от C/B до 1. Вспоминаем, что P — это вероятность того, что ни один член группы не совершит необходимого действия. Следовательно, вероятность, что кто-нибудь из членов группы предпримет необходимое действие (а именно 1 – P), снижается от 1 – C/B = (B – C)/B до 0.
Иными словами, чем больше людей, тем ниже вероятность, что кто-нибудь из них предпримет необходимое действие. На интуитивном уровне это правильно и вполне соответствует концепции диффузии ответственности. Однако это не позволяет нам сделать вывод, что в более многочисленной группе вероятность оказания помощи меньше. Как было сказано выше, помощь требует действий только одного человека. Поскольку увеличивается количество людей, каждый из которых предпримет необходимое действие с убывающей вероятностью, мы не можем прийти к однозначному выводу, что вероятность того, что хотя бы один человек будет действовать, уменьшится. Для того чтобы понять, так ли это, понадобятся дополнительные вычисления.
Учитывая, что N членов группы в случайном порядке, независимо друг от друга, выбирают стратегии в равновесии Нэша, вероятность Q того, что ни один из них не окажет помощи, составляет
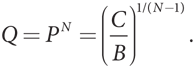
Когда N увеличивается от 2 до бесконечности, N/(N – 1) уменьшается от 2 до 1, а значит, Q увеличивается от (C/B)2 до C/B. Соответственно, вероятность того, что как минимум один человек поможет (то есть 1 – Q), уменьшится от 1 – (C/B)2 до 1 – C/B.
Итак, наши точные расчеты подтверждают гипотезу: чем больше группа, тем меньше вероятность предоставления помощи. Однако вероятность не снижается до нуля даже в очень больших группах, а вместо этого выходит на один уровень, принимая определенное положительное значение, а именно (B – C)/B, зависящее от преимуществ и издержек данного действия для каждого члена группы.
Мы видим, как анализ, основанный на теории игр, подтверждает идеи из области социальной психологии, с которых мы начали. Теория диффузии ответственности позволяет нам пройти часть пути, а именно до вывода о том, что любой человек с меньшей вероятностью совершает необходимое действие, становясь частью более крупной группы. Однако требуемый вывод о том, что более крупные группы с меньшей вероятностью оказывают помощь, нуждается в более точном вычислении вероятности на основании анализа смешивания стратегий каждым отдельно взятым членом группы и полученного в итоге интерактивного равновесия в данной игре.
А теперь хотим спросить: неужели смерть Китти Дженовезе была напрасной? Неужто теории плюралистического неведения и диффузии ответственности, а также игры «безбилетников» по-прежнему проявляются в снижении вероятности действия отдельного человека в постоянно растущих больших городах? Возможно, и нет. Джон Тирни из New York Times публично восхвалял достоинства «городских героев», которые воспитывают в людях цивилизованность посредством немедленного наказания тех, кто демонстрирует неприемлемое поведение — разбрасывает мусор, шумит и вообще относится к категории отбросов общества, заслуживающих порицания. Такие «городские герои», по сути, блюстители выполнения норм сотрудничества в обществе. Анализируя действия известных «героев», Тирни напоминает всем нам: «Необходимо мобилизовать новых героев! В это самое мгновение люди зря тратят время на чтение, тогда как на улицах попираются нормы. …Вы живете не одни в этом мире! Вы обеспечили выполнение нормы сегодня?» Другими словами, нам необходимы социальные нормы, а также избранные люди, которые сделали норму соблюдения норм смыслом своей жизни.
Резюме
Как правило, в играх со многими участниками присутствуют проблемы коллективного действия. Общую структуру коллективных игр можно представить в виде дилеммы заключенных, игры в труса или игры в доверие. Самая большая трудность, связанная с такими играми в любой форме, состоит в том, что равновесие Нэша, проистекающее из рационального выбора отдельных игроков, может не быть социально оптимальным исходом, который максимизирует сумму выигрышей всех игроков.
Когда в играх с коллективным действием действие одного игрока оказывает влияние на выигрыши всех остальных игроков, проявляются внешние эффекты, или экстерналии. Они могут быть положительными или отрицательными и способны привести к продиктованным личными интересами исходам, которые не будут социально оптимальными. Когда действия создают отрицательные сопутствующие эффекты, с точки зрения общества в целом они чересчур активно применяются; когда действия обусловливают положительные сопутствующие эффекты, они недостаточно активны. При наличии положительных сопутствующих эффектов существует такая дополнительная возможность, как положительная обратная связь; при этом в игре может быть несколько равновесий Нэша.
Проблемы коллективного действия волновали ученых из разных областей науки на протяжении многих столетий. В некоторых ранних трудах говорилось об отсутствии в этой ситуации какой-либо перспективы, тогда как другие предлагали кардинальные решения. Авторы последних работ на эту тему признают, что проблемы коллективного действия возникают в самых разных сферах и их универсального решения не существует. Исследования, проведенные в области социологии, показывают, что социальная традиция, или соглашение, может привести к кооперативному поведению. Другие варианты решений связаны с формированием норм приемлемого поведения. Некоторые из этих норм привносятся в виде выигрышей отдельного человека, другие необходимо обеспечивать в принудительном порядке посредством введения санкций в ответ на некооперативное поведение. Авторы большинства работ по этой теме сходятся во мнении, что небольшие группы более эффективно решают проблемы коллективного действия, чем большие.
В играх, проходящих в крупных группах, имеет место диффузия ответственности, которая может обусловить поведение, когда отдельно взятый человек ждет, чтобы другие выполнили необходимое действие, а он взял на себя роль «безбилетника», то есть извлек выгоду из этого действия. Когда кому-то требуется помощь, вероятность ее предоставления снижается по мере увеличения размера группы людей, которые могут ее оказать.
Ключевые термины
Безбилетник
Внешний эффект
Диффузия ответственности
Замыкание
Маржинальная личная выгода
Маржинальная социальная выгода
Маржинальный сопутствующий эффект
Неисключаемые блага
Неконкурентные блага
Норма
Плюралистическое неведение
Положительная обратная связь
Принуждение
Притеснение
Проблема коллективных действий
Санкция
Соглашение
Сопутствующий эффект
Социальный оптимум
Традиция
Чистое общественное благо
Экстерналия
Упражнения с решениями
S1. Предположим, 400 человек выбирают между действиями X и Y. Относительные выигрыши от этих двух действий зависят от того, сколько из 400 человек выберет действие X и сколько — действие Y. Эти выигрыши отображены на представленном ниже графике, но вертикальная ось не обозначена, а значит, вам неизвестно, что именно показывают эти линии — выигрыши или издержки, связанные с этими двумя действиями.
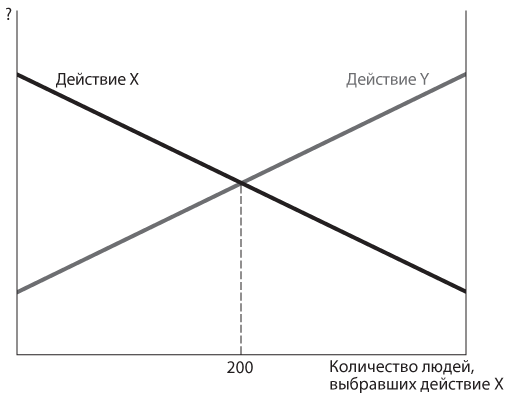
a) Вам сообщают, что исход, при котором 200 человек выберут действие X, — это неустойчивое равновесие. Если 100 человек уже выбрали действие X, то увеличится или уменьшится со временем количество людей, выбирающих действие X? Почему?
b) Для того чтобы график соответствовал поведению, описанному вами в пункте a, должны ли представленные на нем линии быть обозначены как издержки или выгоды от действий X и Y? Обоснуйте свой ответ.
S2. Группа состоит из 100 членов, каждый из которых выбирает, участвовать ли ему в общем проекте. Если n человек решат участвовать, то каждый получит выгоду p(n) = n, а каждый из (100 – n) уклонившихся получит выгоду s(n) = 4 + 3n.
a) Это пример дилеммы заключенных, игры в труса или игры в доверие?
b) Составьте формулу для определения общей выгоды группы.
c) Покажите в графическом либо в математическом виде, что группа получит максимальную общую выгоду при n = 74.
d) Какие трудности возникнут при попытке привлечь к реализации проекта ровно 74 члена группы и позволить остальным 26 членам группы отказаться от него?
e) Как группа может попытаться преодолеть эти трудности?
S3. Рассмотрим небольшой географический регион с общей численностью населения 1 миллион человек. Каждый человек может выбрать, в каком из двух городов жить, Альфавилле или Бетавилле. Какое-то время преимущества проживания в том или ином городе для каждого человека возрастают по мере роста размера города (в крупных городах более развитая инфраструктура и т. д.), но после какого-то момента начинают уменьшаться (в связи с дорожными заторами и т. п.). Если x — доля людей, которые живут в том же городе, что и вы, ваш выигрыш определяется следующими условиями:
x, если 0 ≤ x ≤ 0,4,
0,6 – 0,5x, если 0,4 < x ≤ 1.
a) Постройте такой же график, как на , показывающий преимущества проживания в двух городах, когда доля жителей одного города по сравнению с другим непрерывно меняется от 0 до 1.
b) Равновесие достигается, либо когда оба города населены и их обитатели получают равные выигрыши, либо когда один город (например, Бетавилль) полностью обезлюдел, а жители другого (Альфавилля) получают более высокий выигрыш, чем первый человек, решивший поселиться в Бетавилле. С помощью построенного графика найдите все равновесия Нэша.
c) Теперь рассмотрите динамику процесса адаптации к изменившимся условиям, когда люди постепенно переезжают в город, жители которого уже получают более высокий выигрыш, чем обитатели другого города. Какие из равновесий, найденных в пункте b, сохранят свою устойчивость при такой динамике? Какие окажутся неустойчивыми?
S4. Допустим, в городе с населением 100 человек строится парк развлечений. Для покрытия затрат на строительство необходимы добровольные пожертвования. Каждого жителя просят внести 100 долларов. Чем больше людей внесут свой вклад в строительство парка, тем крупнее он будет и тем больше польза для каждого горожанина. При этом невозможно не допустить в парк тех жителей города, которые не внесли вклад в его создание: они получат свою долю выгоды в любом случае. Предположим, что, когда из всех жителей города n внесут вклад (n может быть любым целым числом от 0 до 100), выгода каждого жителя в денежных единицах составит n2 долларов.
a) Допустим, сначала никто не вносит вклад. Будучи мэром города, вы хотели бы, чтобы все горожане сделали пожертвование, и можете уговорить некоторых из них. Какое минимальное количество жителей города вам нужно убедить, чтобы остальные добровольно присоединились к проекту?
b) Найдите равновесия Нэша в игре, в которой каждый житель города решает, вносить ли ему вклад в создание парка.
S5. Используйте идею кейнсианской безработицы, описанную в , в игре с соответствующими характеристиками и покажите множество равновесий в игре на графике. Отобразите уровень производства (национальный продукт) на вертикальной оси как функцию уровня спроса (национального дохода) на горизонтальной оси. Равновесие достигается, когда национальный продукт равен национальному доходу, то есть когда функция этих двух показателей пересекает линию под углом 45 градусов. При каких формах этой функции возможно множество равновесий? Почему вероятно существование таких форм в реальности? Предположим, доход увеличивается, когда текущий объем производства превышает текущий доход, и снижается, когда текущий объем производства меньше текущего дохода. Какие равновесия устойчивы и какие неустойчивы при таком динамическом процессе?
S6. Составьте краткое описание стратегической игры со многими участниками, свидетелем или участником которой вы были и в которой выигрыши отдельных игроков зависели от количества других игроков и их действий. Попытайтесь проиллюстрировать ее с помощью графика, если это возможно. Опишите исход реальной игры в свете того, что многие подобные игры приводят к неэффективным исходам. Вы видите признаки такого исхода в вашей игре?
Упражнения без решений
U1. На представлены выигрыши в обобщенной коллективной игре с двумя участниками. Там были показаны различные неравенства по алгебраическим выигрышам (p(1) и т. д.), которые делают игру дилеммой заключенных. Вам предстоит найти аналогичные неравенства, соответствующие другим типам игр.
a) При каком условии (условиях) в отношении выигрышей эта игра с двумя участниками представляет собой игру в труса? Какое дополнительное условие (условия) делает эту игру версией I игры в труса (которая показана на )?
b) При каком условии (условиях) в отношении выигрышей эта игра с двумя участниками представляет собой игру в доверие?
U2. Группе из 30 студентов задали домашнее задание, состоящее из пяти вопросов. Первые четыре вопроса — обычные задачи, решение которых в сумме дает 90 баллов. А пятый вопрос — игра на взаимодействие всей группы. В задании сказано: «Вы можете выбрать, отвечать на этот вопрос или нет. Если решите отвечать, просто напишите: “Это мой ответ на вопрос 5”. Если решите не отвечать на вопрос 5, ваша оценка за выполнение домашнего задания будет зависеть от количества баллов, набранных за первые четыре задачи. Если решите ответить на вопрос 5, ваша оценка будет определяться так: если на вопрос 5 ответит меньше половины студентов группы, вы получите 10 баллов и они будут добавлены к баллам за четыре предыдущие задачи, после чего вы получите общую оценку за выполнение домашнего задания. Если на вопрос 5 ответит половина или больше студентов группы, вы получите 10 баллов и они будут вычтены из вашей оценки за предыдущих четыре вопроса».
a) Постройте график, отображающий выигрыши от двух возможных стратегий — «ответить на вопрос 5» и «не отвечать на вопрос 5», в зависимости от количества студентов, отвечающих на этот вопрос. Найдите равновесие Нэша в этой игре.
b) Какого результата игры вы бы ожидали, если бы она действительно проводилась в вашей группе в колледже? Почему? Проанализируйте два случая: 1) студенты делают выбор в индивидуальном порядке, не общаясь друг с другом; 2) студенты делают выбор в индивидуальном порядке, но могут заранее обсудить его на форуме на сайте группы.
U3. Существует два маршрута передвижения из пункта А в пункт Б. Один — скоростная автомагистраль, а другой — местные дороги. Выигрыш от использования автомагистрали представляет собой постоянную величину, равную 1,8, независимо от количества водителей, которые по ней ездят. Местные дороги перегружены, когда ими пользуется слишком много людей, но если по ним передвигается недостаточное количество машин, некоторые водители рискуют стать жертвами преступлений. Предположим, что когда x водителей выбирают местные дороги, выигрыш каждого из них от поездки по такому маршруту определяется по формуле 1 + 9x – 10x2.
a) Постройте график, отображающий преимущества двух маршрутов передвижения как функцию x, рассматривая x в качестве непрерывной переменной, значения которой могут меняться от 0 до 1.
b) На основании графика, полученного в пункте а, определите все возможные равновесные схемы движения транспорта. Какие из этих равновесий устойчивы? Какие неустойчивы? Почему?
c) Какое значение x обеспечивает максимальный выигрыш всей совокупности игроков?
U4. Предположим, группа студентов численностью 100 человек сравнивает две карьеры — юриста и инженера. Инженер получает чистую заработную плату 100 000 долларов в год независимо от того, сколько студентов выберут эту профессию. Юристы обеспечивают работу друг другу, поэтому по мере увеличения их количества растет и уровень их дохода — до определенного момента. В конечном счете конкуренция между юристами приводит к снижению дохода каждого из них. В частности, если есть N юристов, каждый из них получит 100N – N2 долларов в год. Годовой объем затрат на ведение юридической практики (офисное помещение, секретарь, помощники юриста, доступ к справочным онлайн-службам и т. д.) составляет 800 000 долларов. Следовательно, при общем количестве N юристов каждый юрист получит чистыми 100N – N2 – 800 тысяч долларов в год.
a) Постройте график, на котором чистый доход каждого юриста отображен на вертикальной оси, а количество юристов — на горизонтальной. (Нанесите несколько точек, например для 0, 10, 20, …, 90, 100 юристов. Проведите через эти точки линию или используйте компьютерную программу для построения графиков.)
b) Каковы возможные равновесные исходы этой игры в случае, когда игроки делают выбор без координации действий?
c) Допустим, вся группа решает, сколько студентов должны стать юристами с целью обеспечить максимальный общий чистый доход всей группы. Каким будет количество юристов? (Если у вас есть необходимые навыки, воспользуйтесь дифференциальным исчислением, рассматривая N как непрерывную переменную. Если таких навыков нет, примените графические методы или электронную таблицу.)
U5. Группа из 12 стран рассматривает возможность создания валютного союза. Они по-разному оценивают плюсы и минусы такого шага, но каждая страна выиграет от присоединения к союзу и проиграет, отказавшись от него, если большинство стран вступят в союз. Страны упорядочены по степени их желания присоединиться: страна 1 стремится вступить в союз больше всех, а страна 12 — меньше всех. В распоряжении каждой страны два действия — «вступить в валютный союз» и «не вступать в валютный союз». Пусть B(i, n) = 2,2 + n – i — выигрыш страны с порядковым номером i, когда она выбирает стратегию «вступить в валютный союз» и другие n также выбрали эту стратегию. Пусть S(i, n) = i – n — это выигрыш страны с порядковым номером i, когда она предпочитает стратегию «не вступать в валютный союз», а другие n — стратегию «вступить в валютный союз».
a) Покажите, что для страны 1 «вступить в валютный союз» — доминирующая стратегия.
b) Исключив стратегию «не вступать в валютный союз» из стратегий страны 1, покажите, что «вступить в валютный союз» — доминирующая стратегия для страны 2.
c) Продолжив процесс, покажите, что все страны предпочтут стратегию «вступить в валютный союз».
d) Сравните выигрыши в случае такого исхода с выигрышами, которые получат страны при использовании стратегии «не вступать в валютный союз». Сколько стран оказались в худшем положении в результате создания валютного союза?

