Приложение
Отношение к риску и теорема Байеса
1. Отношение к риску и ожидаемая полезность
В мы указали на трудности с использованием вероятностей для вычисления среднего или ожидаемого выигрыша игроков в той или иной игре. Рассмотрим игру, участники которой получают или теряют деньги; предположим, выигрыш в ней равен определенной сумме. Если вероятность не получить ничего составляет 75%, а вероятность получить 100 долларов — 25%, то ожидаемый выигрыш рассчитывается как взвешенное по вероятности среднее; иными словами, он равен среднему значению различных выигрышей, рассчитанному с использованием вероятности в качестве веса. В данном случае мы имеем 0 долларов с вероятностью 75%, что дает в среднем 0,75 × 0 = 0, и 100 долларов с вероятностью 25%, что дает в среднем 0,25 × 100 = 25. Этот же выигрыш игрок получил бы в результате неслучайного исхода, гарантирующего ему 25 долларов каждый раз, когда он играет. Считается, что люди нейтральны по отношению к риску, если для них не имеет значения, что выбирать из различных вариантов с одинаковой денежной стоимостью, но разным уровнем риска. В нашем примере в одном варианте риск отсутствует (игрок получит 25 долларов в любом случае), тогда как другой вариант сопряжен с риском, обеспечивая 0 долларов с вероятностью 0,75 и 100 долларов с вероятностью 0,25, с тем же средним показателем 25 долларов. С другой стороны, есть люди, не расположенные к риску, то есть те, кто из двух вариантов с одинаковой средней денежной стоимостью выберет менее рискованный. В нашем примере они предпочли бы получить 25 долларов наверняка, чем сталкиваться с рискованной перспективой «100 долларов или ничего», и при наличии возможности выбора остановились бы на более безопасном варианте. Такая нерасположенность к риску встречается повсеместно, поэтому нам нужна теория принятия решений в условиях неопределенности, учитывающая этот факт.
В мы также говорили, что незначительное изменение процедуры вычисления выигрышей позволяет обойти эту трудность. Мы сказали, что выигрыши можно измерять не в денежных суммах, а с помощью нелинейной шкалы денежных сумм. В данном приложении мы покажем, как составить такую шкалу и почему это решает нашу проблему.
Предположим, когда человек получает D долларов, мы исходим из того, что его выигрыш составляет не просто D, а, например, √D. Тогда выигрыш от 0 долларов равен 0, а выигрыш от 100 долларов равен 10. Такое преобразование не меняет способа оценки двух выигрышей в размере 0 долларов и 100 долларов, а просто определенным образом меняет шкалу выигрышей.
Теперь проанализируем рискованную перспективу получения 100 долларов с вероятностью 0,25 и отсутствия какого бы то ни было выигрыша в противном случае. После изменения шкалы ожидаемый выигрыш (представляющий взвешенное по вероятности среднее двух выигрышей) составляет (0,75 × 0) + (0,25 × 10) = 2,5. Он эквивалентен квадратному корню из полученной денежной суммы. Поскольку 2,5 = √625, выигрыш человека, который наверняка получит 6,25 доллара, также составит 2,5. Другими словами, в случае применения шкалы выигрышей в виде квадратного корня человек был бы одинаково рад получить 6,25 доллара наверняка и 100 долларов с вероятностью 25 процентов. Подобное безразличие к гарантированным 6,25 доллара и 100 долларам в одном из четырех случаев свидетельствует о сильной нерасположенности к риску: этот человек готов пожертвовать разностью между 25 долларами и 6,25 доллара ради того, чтобы его избежать. На рис. 8П.1 показана эта нелинейная шкала (квадратный корень), ожидаемый выигрыш и безразличие человека к выбору между беспроигрышным и рискованным вариантом развития событий.
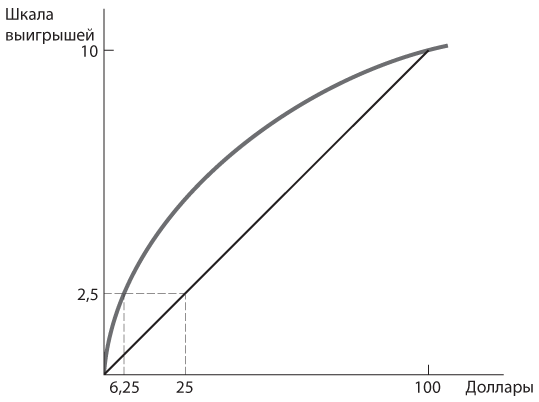
Рис. 8П.1. Вогнутая шкала: нерасположенность к риску
Но что если нелинейная шкала, используемая нами для изменения шкалы долларовых выигрышей, содержит кубический, а не квадратный корень? Тогда выигрыш от получения 100 долларов равен 4,64, а ожидаемый выигрыш от рискованного варианта составляет (0,75 × 0) + (0,25 × 4,64) = 1,16, то есть кубический корень из 1,56. Следовательно, человек с такой шкалой выигрышей наверняка получит только 1,56 доллара вместо рискованного варианта, обеспечивающего ему в среднем 25 долларов. Это означает, что у такого человека действительно очень высокий уровень нерасположенности к риску. (Для того чтобы понять, почему ситуация обстоит именно так, сравните график кубического корня из x с графиком квадратного корня из x.)
А что если изменение шкалы выигрышей, исчисляемых в x долларов, выполнить с помощью функции x2? Ожидаемый выигрыш от рискованного варианта составит (0,75 × 0) + (0,25 × 10 000) = 2500, что равно 50 в квадрате. Стало быть, при такой шкале выигрышей человеку будет безразлично, получит ли он 50 долларов в любом случае или рискнет с ожидаемой денежной стоимостью всего 25 долларов. Этот человек должен быть склонен к риску, поскольку не желает отдавать деньги в обмен на его снижение; напротив, ему необходимо дать дополнительных 25 долларов в качестве компенсации за потерю риска. На рис. 8П.2 изображена нелинейная шкала, которой соответствует функция x2.
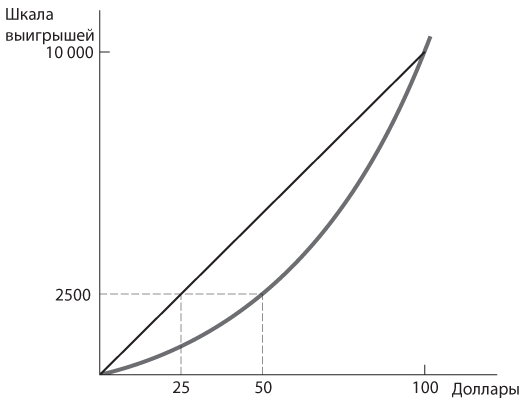
Рис. 8П.2. Выгнутая шкала: склонность к риску
Таким образом, использование разных вариантов нелинейной шкалы выигрышей вместо чистых денежных выигрышей позволяет определить разные степени неприятия риска или склонности к нему. Вогнутая шкала () соответствует нерасположенности к риску, а выгнутая (рис. 8П.2) — склонности к риску. Вы можете поэкспериментировать с другими простыми вариантами нелинейной шкалы (такими как логарифмы, экспоненциальные функции и другие корни и степени), чтобы выяснить, что они говорят об отношении к риску.
Этот метод оценки рискованных перспектив имеет давнюю традицию в теории принятия решений и обозначается термином «метод ожидаемой полезности». Нелинейная шкала, которая позволяет вычислить выигрыши как функцию денежной стоимости, называется функцией полезности; квадратный и кубический корни и квадрат — простые примеры такой функции. Математическое ожидание, или взвешенное по вероятности среднее значений полезности различных денежных сумм при случайном варианте развития событий, называется ожидаемой полезностью этого варианта. Различные случайные варианты сравниваются друг с другом по их ожидаемой полезности; варианты с более высокой ожидаемой полезностью считаются более приемлемыми, чем варианты с более низкой ожидаемой полезностью.
Почти вся теория игр основана на методе ожидаемой полезности, и он действительно чрезвычайно полезен, хотя и не лишен недостатков. Мы возьмем его на вооружение в данной книге, а более подробный анализ оставим для научных трудов повышенного уровня сложности.
2. Вывод вероятностей из наблюдаемых последствий
Когда участники игры владеют разным объемом информации, они попытаются использовать какой-то инструмент для выяснения личной информации соперника. Как мы говорили в данной главы, иногда непосредственная коммуникация позволяет достичь равновесия дешевого разговора. Но более типична ситуация, когда игрокам приходится определять информацию соперников посредством наблюдения за их действиями. В таком случае они должны оценить вероятность исходной информации с помощью этих действий или их наблюдаемых последствий. Такая оценка требует относительно сложных манипуляций с правилами исчисления вероятностей, и мы изучим этот процесс более подробно.
Правила вычисления вероятности событий, изложенные в , в частности правило определения комбинации вероятностей, весьма полезны для вычисления выигрышей в случаях, когда игроки располагают разным объемом информации. В играх с асимметричной информацией участники пытаются выяснить информацию, имеющуюся у соперников, посредством наблюдения за их действиями и последующих выводов (оценивания) вероятности исходной информации на основе наблюдаемых действий или их результатов.
Лучше всего это проиллюстрировать на примере. Предположим, у 1% населения есть генетический дефект, который может вызвать определенное заболевание. Тест, позволяющий обнаружить этот дефект, имеет 99% точности: при наличии дефекта тест не сможет его выявить в 1% случаев, а при отсутствии может ошибочно найти в 1% случаев. Другими словами, мы не можем непосредственно наблюдать этот дефект у человека (исходное условие), но можем наблюдать результаты теста на его наличие (последствия) — вот только тест не идеальный индикатор дефекта. В какой степени, учитывая наши наблюдения, мы можем быть уверены, что исходное условие действительно выполняется?
Для того чтобы ответить на этот вопрос в контексте нашего конкретного примера, мы можем произвести простые численные расчеты. Рассмотрим совокупность из 10 000 человек, в которой у 100 человек (1%) есть дефект, а у 9900 — нет. Предположим, все они пройдут тест. Из 100 человек с дефектом тест даст правильный положительный результат у 99 человек. Из 9900 человек без дефекта тест покажет ошибочный положительный результат тоже у 99 человек. Итого будет получено 198 положительных результатов, из которых половина правильные и половина неправильные. Если человек получит положительный результат теста, это может произойти как потому, что тест действительно выявил патологию, так и по причине ошибки. Следовательно, риск того, что у человека с положительным результатом теста на самом деле есть дефект, составляет всего 50%. (Именно поэтому тесты на обнаружение редких патологий необходимо разрабатывать так, чтобы они обеспечивали очень низкий коэффициент получения ложных положительных результатов.)
Для ответа на общие вопросы такого типа мы используем алгебраическую формулу под названием «теорема Байеса», которая позволяет поставить задачу и произвести необходимые вычисления. Для этого обобщим наш пример, допустив два варианта исходных условий, A и B (скажем, есть генетический дефект или нет), и два наблюдаемых последствия, X и Y (например, положительный или отрицательный результат теста). Предположим, что при отсутствии информации (по всей популяции) вероятность выполнения условия А равна p, а значит, вероятность выполнения условия B составляет (1 – p). В случае выполнения условия A вероятность наблюдения X равна a, стало быть, вероятность наблюдения Y составляет (1 – a). (В терминах, сформулированных нами в , a — это вероятность X при условии A, тогда как (1 – a) — это вероятность Y при условии A.) Аналогичным образом при выполнении условия B вероятность наблюдения X равна b, а вероятность наблюдения Y — (1 – b).
Это описание указывает на возможные четыре альтернативные комбинации событий: 1) выполняется A, наблюдается X; 2) выполняется A, наблюдается Y; 3) выполняется B, наблюдается X; 4) выполняется B, наблюдается Y. Модифицированное правило умножения позволяет определить вероятности этих четырех комбинаций: pa, p(1 – a), (1 – p)b и (1 – p)(1 – b) соответственно.
Теперь предположим, что наблюдается X: человек проходит тест на наличие генетического дефекта и получает положительный результат. Тогда мы фокусируемся на подмножестве вышеперечисленных возможностей, а именно на первой и третьей комбинации, включающих в себя наблюдение X. В этом подмножестве исходов с наблюдаемым X вероятность того, что A также выполняется, составляет pa, как показано выше. Таким образом, нам известно, с какой вероятностью мы можем наблюдать только X и с какой вероятностью — как X, так и A.
Но нас больше интересует определение вероятности того, что A выполняется при условии, что мы наблюдали X, то есть что у человека есть генетический дефект в случае положительного результата теста. Вычисление этой вероятности довольно сложное. Согласно модифицированному правилу умножения, вероятность того, что имеет место как A, так и X, равна произведению вероятности того, что имеет место X, на вероятность A при условии X. Нас интересует именно эта последняя вероятность. Воспользовавшись выведенными выше формулами для вычисления «A и X» и «только X», получим
Prob(A и X) = Prob(только X) × Prob(A при условии X),
pa = [pa + (1 – p)b] × Prob(A при условии X),
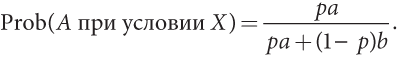
Формула дает оценку вероятности того, что A выполнялось при условии, что мы наблюдали X (и поэтому поставили все в зависимость от этого факта). Этот результат известен как теорема Байеса (а также как правило, или формула, Байеса).
В нашем примере с тестированием на наличие генетического дефекта были такие значения: Prob(A) = p = 0,01, Prob(X при условии A) = a = 0,99 и Prob(X при условии B) = b = 0,01. Мы можем подставить их в формулу Байеса и получим вероятность наличия дефекта при условии положительного результата теста = Prob(A при условии X)
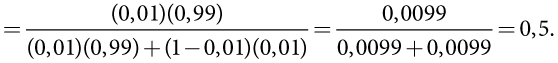
Алгебраические операции с вероятностями, проведенные с помощью правила Байеса, подтверждают результат арифметических вычислений (основанных на перечислении всех возможных случаев), которые мы использовали выше. Преимущество формулы состоит в том, что ее можно применять механически, что позволяет избежать трудоемкого и подверженного ошибкам процесса перечисления всех возможных вариантов и определения всех необходимых вероятностей.
На рис. 8П.3 правило Байеса представлено в виде таблицы, так его легче запомнить и использовать, чем формулу. В строках таблицы отображаются истинные альтернативные условия, которые могут существовать, например «генетический дефект» и «отсутствие генетического дефекта». У нас всего два варианта, A и B, но этот метод можно обобщить на любое количество возможных исходов. В столбцах таблицы отображаются наблюдаемые события — например, «положительный результат теста» и «отрицательный результат теста».

Рис. 8П.3. Правило Байеса
В каждой ячейке таблицы представлена совместная вероятность соответствующей комбинации исходного условия и наблюдения; это и есть вероятности перечисленных выше четырех комбинаций возможных вариантов. В последнем столбце справа отображена сумма по первым двум столбцам каждой из верхних двух строк. Она представляет собой общую вероятность каждого истинного условия (так, например, вероятность A равна p, как мы уже видели). В последней строке отображена сумма первых двух строк в каждом столбце. Например, запись в последней строке столбца X — это общая вероятность наблюдения X, либо когда A — истинное условие (правильный положительный результат в примере с генетическим тестом), либо когда B — истинное условие (ошибочный положительный результат).
Для того чтобы вычислить вероятность того или иного условия с учетом определенного наблюдения, согласно правилу Байеса, необходимо взять запись из ячейки, соответствующей комбинации этого условия и наблюдения, и разделить данное значение на сумму по столбцу в последней строке этого наблюдения. В качестве примера можно привести
Prob(B при условии X) = (1 – p)b / [pa + (1 – p)b].
Резюме
Оценка последствий на основании ожидаемых денежных выигрышей подразумевает нейтральное отношение к риску. Нерасположенность к риску можно учесть с помощью метода ожидаемой полезности, который требует использования функции полезности, представляющей вогнутую шкалу денежных выигрышей, а также принятия взвешенного по вероятности среднего значения в качестве меры ожидаемого выигрыша.
Если участники игры располагают асимметричной информацией, они могут попытаться вывести вероятности скрытых исходных условий посредством наблюдения за действиями или их последствиями. Теорема Байеса предоставляет формулу для определения таких вероятностей.
Ключевые термины
Нейтральное отношение к риску
Нерасположенность к риску
Ожидаемая полезность
Теорема Байеса
Функция полезности

