5. Сигнализирование на рынке труда
Многие из вас рассчитывают по окончании учебы работать в элитной финансовой или ИТ-компании. В таких компаниях существует два типа вакансий. Один тип требует высокого уровня математических и аналитических навыков, а также способности усердно трудиться и оплачивается очень хорошо. Другой — это отчасти административная, менее квалифицированная, низкооплачиваемая работа. Безусловно, вы мечтаете о высокооплачиваемой работе. Вы знаете свои качества и навыки гораздо лучше, чем ваш потенциальный работодатель. Если у вас высокий уровень квалификации, вам необходимо, чтобы работодатель узнал об этом, к тому же он тоже хочет это знать. Работодатель может проверить ваши данные и провести с вами собеседование, но информация, полученная таким способом, ограничена имеющимися в его распоряжении временем и ресурсами. Вы можете рассказать работодателю, насколько вы опытный специалист, но подобные голословные заявления не внушают доверия. Вы должны чем-то подкрепить их, а ваш работодатель — попытаться получить более объективные данные.
Какие доказательства может искать работодатель, и что вы можете ему предоставить? Как говорилось в данной главы, ваш потенциальный работодатель применит определенные инструменты скрининга для определения ваших качеств и навыков. Вы, в свою очередь, будете использовать сигналы для передачи фактически той же информации. Иногда для сигнализирования или скрининга могут применяться подобные или даже идентичные инструменты.
В данном примере выбранный вами (и прослушанный) особенно трудный математический курс в университете может выступать в качестве достоверного доказательства вашей способности напряженно работать в целом и ваших математических и логических навыков в частности. Давайте проанализируем роль выбора курса обучения в качестве инструмента скрининга.
А. Скрининг в целях разделения типов
Для простоты проанализируем эту скрининговую игру с помощью интуиции и алгебры. Допустим, с точки зрения качеств, которые представляют интерес для работодателей, студенты делятся всего на два типа: талантливые (Т) и посредственные (П). Потенциальные работодатели из сферы финансов или информационных технологий готовы платить 160 000 долларов в год типу Т и 60 000 в год типу П. Другие работодатели предлагают типу Т 125 000 долларов, а типу П 30 000 долларов. Это те же показатели, что и в примере с автомобилями Citrus в , только умноженные на 10, чтобы они больше соответствовали реальному положению дел на рынке труда. И точно так же как в примере с подержанными автомобилями мы исходили из предположения о фиксированном запасе автомобилей и большом количестве потенциальных покупателей, здесь мы исходим из того, что у нас много потенциальных работодателей, вынужденных конкурировать друг с другом за ограниченное число кандидатов на вакантные должности, поэтому они должны предлагать им максимальную заработную плату, которую готовы выплачивать. Поскольку работодатели не могут определить тип конкретного претендента на ту или иную должность посредством прямых наблюдений, им необходимо найти другие надежные способы провести различие между типами.
Допустим, два типа студентов отличаются друг от друга готовностью изучать трудный, а не легкий курс в университете. Представители каждого типа готовы пожертвовать частью времени, выделенного на вечеринки и другие занятия, на изучение более трудного курса, но для студентов типа Т эта жертва меньше и пойти на нее легче, чем студентам типа П. Предположим, студенты типа Т рассматривают затраты на прохождение каждого такого курса как эквивалент годовой заработной платы в размере 3000 долларов, а студенты типа П — как 15 000 долларов. Может ли работодатель использовать эту разницу для скрининга кандидатов, чтобы отличить тип Т от типа П?
Рассмотрим следующую политику найма: любой студент, прослушавший определенное количество (n) сложных курсов, будет отнесен к типу Т и получит заработную плату в размере 160 000 долларов, и любой, кто изучил менее n сложных курсов, будет отнесен к типу П и получит 60 000 долларов. Цель такой политики — создание естественных стимулов, под влиянием которых только студенты типа Т будут изучать сложные курсы, а студенты типа П не станут этого делать. Ни один тип не намерен проходить больше сложных курсов обучения, чем требуется, поэтому варианты выбора таковы: либо изучить n курсов, чтобы претендовать на тип Т, либо признать поражение и согласиться на тип П (эти студенты могут вообще отказаться от изучения сложных курсов и просто учиться, не прилагая к этому особых усилий).
Чтобы такая политика найма достигла цели, она должна удовлетворять двум видам условий. Первый требует, чтобы политика найма стимулировала кандидатов каждого типа сделать тот выбор, который нужен компании. Иными словами, она должна быть совместима со стимулами сотрудников, поэтому соответствующие условия обозначаются термином условия совместимости стимулов. Второй вид условий гарантирует, что при выборе, продиктованном условиями совместимости стимулов, сотрудники получат лучший (по крайней мере не худший) выигрыш от соответствующих должностей, чем они получили бы в случае выбора другого варианта. То есть сотрудники должны согласиться на участие в предложенном компанией плане, поэтому соответствующие условия называются условиями участия. Мы рассмотрим их в контексте рынка труда чуть ниже. Аналогичные условия будут упоминаться и в других примерах, приведенных далее в этой главе и в , где описывается общая теория разработки подобных механизмов.
I.-Совместимость стимулов. Критерий, разработанный работодателями, чтобы отличить тип Т от П (а именно, количество изученных сложных курсов), должен быть достаточно строгим, чтобы студенты типа П даже не пытались удовлетворить его, но не настолько строгим, чтобы лишить студентов типа Т желания предпринимать подобные попытки. Правильное значение n должно быть таким, чтобы студенты, действительно принадлежащие к типу П, признали это и согласились на 60 000 долларов, вместо того чтобы нести дополнительные издержки в связи с имитацией поведения студентов типа Т. Иначе говоря, нам нужно, чтобы политика найма была совместима по стимулам с типом П, поэтому
60 000 ≥ 160 000 – 15 000n, или 15n ≥ 100, или n ≥ 6,67.
Аналогичным образом условие, согласно которому студенты, действительно принадлежащие к типу Т, предпочитают доказать это посредством изучения n сложных курсов, выглядит так:
160 000 – 3000n ≥ 60 000, или 3n ≤ 100, или n ≤ 33,33.
Эти условия совместимости стимулов, или, что то же самое, ограничения совместимости стимулов, приводят стимулы кандидата на должность в соответствие с требованиями работодателя или делают оптимальным для кандидата раскрытие правдивой информации об уровне квалификации посредством своих действий. Значение n удовлетворяет обоим ограничениям, если это целое число в диапазоне от 7 до 33. Второе значение не совсем уместно в данном примере, поскольку программа обучения в колледже обычно состоит из 32 курсов, но в других примерах это может иметь смысл.
Удовлетворение обоим условиям обеспечивает разница в издержках в связи с изучением сложных курсов между двумя типами: эти издержки существенно ниже для студентов «хорошего» типа, которых и ищут работодатели. Когда ограничения удовлетворены, работодатель может использовать политику найма, на которую студенты двух типов отреагируют по-разному, тем самым раскрывая свой тип. Данный процесс называется разделением типов на основе самоотбора.
Мы не учли здесь вероятности того, что на самом деле сложные курсы обучения позволяют овладеть дополнительными навыками или методами работы, способными превратить студентов типа П в тип Т. Согласно нашему сценарию, сложные курсы служат только цели идентификации людей, которые уже обладают соответствующими качествами. Другими словами, эти курсы выполняют лишь функцию скрининга.
В реальной жизни образование действительно повышает продуктивность. Но помимо этого оно еще выполняет функцию сигнализирования и скрининга того вида, о котором идет речь в данном разделе. В нашем примере мы показали, что образование может быть получено исключительно ради второй функции; на самом деле оно часто превышает уровень, необходимый только для роста продуктивности. Такое дополнительное образование сопряжено с издержками асимметричности информации.
II.-Участие. Когда условия совместимости стимулов для двух типов рабочих мест в данной компании удовлетворены, студенты типа Т изучают n сложных курсов и получают выигрыш в размере 160 000 – 3000n, тогда как cтуденты типа П не проходят сложных курсов и получают выигрыш 60 000. Чтобы студенты обоих типов были готовы сделать именно такой выбор вместо использования альтернативных возможностей, нужно, чтобы удовлетворялись также условия участия. Поэтому нам необходимо следующее неравенство:
160 000 – 3000n ≥ 125 000, или 3n ≤ 35, или n ≤ 11,67.
В данном примере очевидно, что условие участия студентов типа П удовлетворяется (хотя в других примерах может быть иначе), а условие участия студентов типа Т требует, чтобы n ≤ 11,67 или, поскольку n должно быть целым числом, n ≤ 11. Здесь любое значение n, которое удовлетворяет ограничению участия студентов типа Т n ≤ 11, удовлетворяет также ограничению совместимости стимулов n ≤ 33, поэтому второе условие становится логически избыточным.
В таком случае полная совокупность условий, выполнение которых необходимо для разделения типов на данном рынке труда, выглядит так: 7 ≤ n ≤ 11. Такое ограничение возможных значений n объединяет условие совместимости стимулов для студентов типа П и условие участия для студентов типа Т. В данном примере условие участия для студентов типа П и условие совместимости стимулов для студентов типа Т автоматически удовлетворяется в случае выполнения всех остальных условий.
Когда в качестве инструмента скрининга используется требование о прохождении достаточного количества сложных курсов, издержки несут студенты типа Т. Если предположить, что для обеспечения разделения типов используется минимальное количество курсов (а именно n = 7), издержки для каждого студента типа Т в денежном выражении составят 7 × 3000 = 21 000 долларов. В данном контексте это и есть издержки асимметричности информации. Их не существовало бы, если бы тип студента можно было определить напрямую и объективно. Не было бы их и в случае, если бы вся совокупность состояла исключительно из студентов типа Т. Последним приходится нести эти издержки по причине наличия в общей совокупности студентов типа П, от которых они (или их потенциальные работодатели) хотят отмежеваться.
Б. Объединение типов
А может, чтобы не возлагать на тип Т издержки асимметричности информации, лучше вообще не утруждать себя разделением типов? При разделении студенты типа Т получают заработную плату 160 000 долларов, но несут издержки в размере 21 000 долларов в связи с изучением сложных курсов; следовательно, их чистый выигрыш в денежном эквиваленте составляет 139 000 долларов. А студенты типа П получают заработную плату 60 000 долларов. Что произойдет с этими типами, если их не разделять?
Отказ от использования инструментов скрининга приведет к случайному выбору кандидатов из общей совокупности и выплате всем одинаковой заработной платы. Такая ситуация называется объединением типов, или просто объединением, когда понятен смысл происходящего. На конкурентном рынке труда в случае объединения типов общая заработная плата является средним значением той ценности, которую представляют собой специалисты разных типов для работодателя, и она зависит от доли каждого типа в общей совокупности. Например, если 60% совокупности — тип Т, а 40% — тип П, общая заработная плата при объединении типов составит:
0,6 × 160 000 + 0,4 × 60 000 = 120 000 долларов.
Естественно, в этом случае специалисты типа Т предпочтут ситуацию с разделением типов, поскольку это обеспечит им 139 000 долларов вместо 120 000. Однако если доли типов в общей совокупности составляют 80% типа Т и 20% типа П, то общая заработная плата при объединении будет 140 000 долларов, а значит, при разделении представители типа Т проиграют. Типу П всегда выгоднее объединение. Наличие типа Т в совокупности означает, что общая заработная плата при объединении типов всегда будет превышать заработную плату представителей типа П в размере 60 000 долларов в случае разделения.
Тем не менее если оба типа предпочтут результат, полученный при объединении, это не может быть равновесием в ситуации, когда многие работодатели или работники конкурируют друг с другом в процессе сигнализирования и скрининга. Предположим, соотношение типов в общей совокупности составляет 80 на 20 и имеет место исходная ситуация с объединением, в которой обоим типам платят по 140 000 долларов. Работодатель может объявить, что готов платить 144 000 долларов тому, кто прослушает всего один сложный курс. По сравнению с исходной ситуацией студенты типа Т сочтут это предложение выгодным, так как их расходы на изучение курса составляют всего 3000 долларов, а заработная плата повышается на 4000 долларов. Поскольку данный работодатель выборочно привлекает студентов типа Т, каждый из которых имеет ценность 160 000 долларов, но получает 144 000 долларов, он извлечет прибыль из отклонения от размера заработной платы, рассчитанного с учетом объединения типов.
Однако такое отклонение запускает процесс корректировки заработной платы конкурирующими работодателями, что приводит к разрушению исходной ситуации с объединением типов. Когда сотрудники типа Т начинают массово переходить к данному работодателю, это приводит к снижению общего уровня квалификации оставшихся у других работодателей специалистов и в итоге наступает момент, когда они уже не в состоянии платить им 140 000 долларов. После снижения заработной платы в совокупности специалистов разница между нею и суммой 144 000 долларов, предложенной вышеупомянутым работодателем, достигнет величины, при которой специалисты типа П также сочтут необходимым пройти один сложный курс обучения. Но тогда этот работодатель вынужден будет повысить свое требование до двух сложных курсов, а разницу в заработной плате до такого уровня, при котором изучение двух курсов станет слишком обременительным для типа П, но вполне приемлемым для типа Т. Другие работодатели, которые тоже захотят привлечь какое-то количество представителей типа Т, должны использовать аналогичную политику найма. Этот процесс будет продолжаться до тех пор, пока рынок труда не достигнет разделяющего равновесия, о котором шла речь выше.
Даже если работодатели не проявят инициативу по привлечению сотрудников типа Т вместо типа П, специалист типа Т, зарабатывающий 140 000 долларов в ситуации с объединением типов, может прослушать сложный курс обучения, принести подтверждающий это документ работодателю и сказать: «У меня есть сертификат о прохождении сложного курса обучения, поэтому я прошу повысить мне зарплату до 144 000 долларов. Это убедительное доказательство того, что я отношусь к типу Т; ни один представитель типа П не сделал бы вам подобного предложения». Учитывая имеющиеся в данной ситуации факты, аргумент можно считать обоснованным, и работодателю было бы выгодно согласиться: сотрудник типа Т представлял бы для него ценность 160 000 долларов, но при этом получал бы 144 000 долларов. Другие специалисты типа Т могут поступить так же. Это запускает тот же каскадный процесс, который приводит к разделяющему равновесию. Единственное различие — кто именно инициатор. Теперь специалисты типа Т решают получить дополнительное образование в качестве достоверного доказательства своего типа, и это уже сигнализирование, а не скрининг.
Общая идея такова: хотя объединение типов может быть выгодно всем, игроки не выбирают то или другое в ходе кооперативного, связующего процесса. Они преследуют собственные интересы, что приводит к формированию разделяющего равновесия. Эта ситуация напоминает игру «дилемма заключенных» со многими участниками, а значит, в издержках асимметричности информации присутствует элемент неизбежности.
В. Множество типов
Хотя мы рассмотрели пример с двумя типами, этот анализ можно обобщить. Предположим, существует несколько типов: А, Б, В, …, сгруппированных в порядке снижения их ценности для работодателя и повышения расходов на получение дополнительного образования. Это позволит установить последовательность постепенно повышающихся требований к уровню образования: самый худший тип в нем не нуждается вообще, следующему типу достаточно самого низкого уровня образования, третий тип должен иметь такой-то уровень и т. д.; при этом представители соответствующих типов будут сами выбирать уровень образования, который их идентифицирует.
В заключение хотим высказать еще одну мысль, или даже предостережение, в отношении сигнализирования. Вы — информированная сторона, и вам доступно действие, которое может достоверно передать хорошую информацию (то есть ту, что наверняка пойдет вам на пользу). Если вам не удастся отправить такой сигнал, это будет воспринято как плохая информация. В этом отношении сигнализирование подобно игре в труса: если вы откажетесь играть, вы уже сыграли и проиграли.
Вы должны помнить об этом, решая, какой курс выбрать — тот, который оценивается по буквенной системе или по принципу «зачтено / не зачтено». Студенты, изучающие тот или иной курс, получают весь диапазон оценок; предположим, средняя оценка — B. Очевидно, что каждый студент прекрасно знает свои способности. У студентов, достаточно уверенных в получении оценки A+, есть мощный стимул пройти сложный курс, который оценивается по буквенной системе. Если они это сделают, средняя оценка остальных студентов окажется меньше B, скажем B−, поскольку это экстремальное значение исключается из распределения. Теперь уже студенты, рассчитывающие на оценку «A», заинтересованы в выборе курса с буквенной системой оценивания, что, в свою очередь, снижает среднюю оценку остальных, и т. д. В итоге студенты выбирают курс, который оценивается по принципу «зачтено / не зачтено», но это касается лишь тех, кто надеется на оценки C и D. Стратегически грамотный читатель приложения к диплому (потенциальный работодатель или член приемной комиссии вуза) знает, что курс с системой оценивания «зачтено / не зачтено» в основном выбирают студенты из нижней части распределения оценок. По этой причине он воспримет оценку «зачтено» как C или D, а не как среднюю оценку всей группы B.
6. Равновесия в сигнальных играх с двумя участниками
До сих пор наш анализ охватывал общую концепцию неполной информации, а также конкретные стратегии сигнализирования и скрининга. Кроме того, мы рассмотрели возможные результаты разделения или объединения типов, которые могут возникнуть вследствие применения этих стратегий. Мы видели, как на рынке с большим количеством владельцев автомобилей и покупателей может сформироваться неблагоприятный отбор, а также как работают инструменты сигнализирования и скрининга в условиях взаимодействия работодателей и работников. Тем не менее мы еще не описали в этой главе решения игры с участием двух игроков, владеющих разной информацией. Ниже приводится пример решения такой игры с использованием дерева игры и таблицы выигрышей в качестве инструментов анализа. Мы увидим, что равновесием в ней может быть либо разделение, либо объединение типов, а также высока вероятность формирования частично раскрывающего или полуразделяющего равновесия.
А. Базовая модель и структура выигрышей
В данном разделе мы проанализируем игру с асимметричной информацией «выход на рынок», в качестве участников которой выступают две автомобилестроительные компании, Tudor и Fordor. В настоящее время корпорация Tudor имеет монополию на рынке автомобилей определенного типа, скажем экономичных малолитражек, не загрязняющих окружающую среду. Инновационная компания Fordor разработала конкурирующую концепцию автомобиля и решает, стоит ли ей выходить на рынок. Однако Fordor не знает, насколько жестким конкурентом окажется Tudor. В частности, издержки производства компании Tudor (о которых Fordor ничего не известно) могут быть высокими или низкими. Если они высокие, Fordor может выйти на рынок и вступить в конкурентную борьбу, получая прибыль; если низкие, выход Fordor на рынок и затраты на разработку невозможно будет возместить за счет операционной прибыли, а значит, ее выход на рынок будет абсолютно убыточным.
Взаимодействие между компаниями представляет собой игру с последовательными ходами. На ее первом этапе (период 1) Tudor устанавливает цену (для простоты предположим, что высокую или низкую), зная, что она единственный производитель автомобилей такого класса на рынке. На следующем этапе Fordor принимает решение о выходе на рынок. Выигрыши (или прибыль) компаний определяются на основании рыночной цены автомобиля с учетом издержек производства каждой компании, а в случае Fordor еще и с учетом затрат в связи с выходом на рынок и разработку автомобиля.
Безусловно, для Tudor было бы лучше, если бы Fordor не выходила на рынок, поэтому на первом этапе игры Tudor может попытаться использовать цену автомобиля как сигнал об издержках производства. Компания с низкими издержками установила бы более низкую цену, чем с высокими. Следовательно, Tudor может рассчитывать на то, что, если на протяжении периода 1 она сохранит низкую цену на автомобиль, Fordor интерпретирует это как доказательство низких издержек производства Tudor и не станет выходить на рынок. (Как только Fordor откажется от дальнейшей борьбы и уйдет со сцены, Tudor может снова поднять цену на авто.) Подобно тому как в покере игрок может блефовать, рассчитывая на то, что это сработает и соперник сбросит карты, Tudor также может попытаться удержать Fordor от выхода на рынок посредством блефа. Разумеется, компания Fordor — стратегический игрок и знает о подобном трюке. Вопрос в том, сможет ли Tudor успешно блефовать в случае равновесия в данной игре. Ответ зависит от вероятности того, что в Tudor действительно низкие издержки производства, а также от затрат на введение конкурента в заблуждение. Ниже мы проанализируем различные варианты развития событий и покажем полученные в результате равновесия.
Во всех этих случаях затраты на единицу продукции и цены выражены в тысячах долларов, а количество проданных автомобилей — в сотнях тысяч, поэтому прибыль измеряется в сотнях миллионов. Это поможет нам представить выигрыши и таблицы в достаточно компактной, удобной для чтения форме. Мы вычислим выигрыши с помощью тех же инструментов анализа, которые применяли в игре с ценообразованием в ресторанах в , при этом будем исходить из предположения, что зависимость между назначенной ценой (P) и величиной спроса (Q) описывается формулой: P = 25 – Q30.
Чтобы выйти на рынок, компания Fordor должна понести первоначальные затраты в размере 40 (в тех же единицах, что и прибыли, в сотнях миллионов, то есть фактический показатель составит 4 миллиарда долларов) на строительство завода, проведение рекламной кампании и т. д. Если затем она выходит на рынок, затраты на производство и поставку на рынок каждого автомобиля составят 10 (тысяч долларов).
Tudor может быть либо громоздкой старой компанией с высокими издержками производства на единицу продукции, составляющими 15 (тысяч долларов), либо динамичным автопроизводителем с более низкими затратами на единицу продукции. Для начала допустим, что более низкие издержки составляют 5; этот показатель ниже затрат, которые может обеспечить Fordor. В и мы проанализируем эффект других уровней издержек. Пока же предположим, что Tudor может обеспечить более низкий уровень издержек с вероятностью 0,4, или в 40% случаев; следовательно, вероятность того, что в этой компании высокий уровень издержек, равна 0,6, или 60%.
Варианты выбора компании Fordor в игре «выход на рынок» зависят от того, что ей известно об издержках Tudor. Будем считать, что Fordor располагает информацией о двух возможных уровнях издержек и может вычислить прибыль в каждом из этих случаев. Таким образом, хотя Fordor неизвестно, к какому типу относится Tudor, предварительное убеждение Fordor в точности соответствует вероятности того, что в Tudor более низкий уровень издержек; иными словами, убеждение Fordor состоит в том, что вероятность вступить в борьбу с Tudor, имеющей низкий уровень издержек производства, составляет 40%.
Если в Tudor высокий уровень издержек, например 15 (тысяч долларов), то в случае монополии, которой ничего не угрожает, компания максимизирует свою прибыль, установив на автомобили цену 20 (тысяч долларов). При такой цене Tudor продаст 5 (сотен тысяч) автомобилей и заработает 25 [= 5 × (20 – 15) сотен миллионов долларов, или 2,5 миллиарда долларов]. Если Fordor выйдет на рынок и составит конкуренцию Tudor, то равновесие Нэша в этой игре в дуополию обеспечит Tudor операционную прибыль 3, а Fordor 45. Эта операционная прибыль превышает первоначальные затраты Fordor в связи с выходом на рынок (40), поэтому если бы компания знала, что в Tudor высокий уровень издержек, она решила бы выйти на рынок и заработать чистую прибыль в размере 5.
Если в Tudor низкий уровень затрат (5), то при наличии монополии, которой ничто не угрожает, компания установит на свои автомобили цену 15, продаст 10 и заработает прибыль 100. В случае равновесия, сформировавшегося на втором этапе игры после выхода на рынок Fordor, операционная прибыль Tudor составит 69, а Fordor 11, что меньше затрат Fordor в связи с выходом на рынок (40). Следовательно, если бы Fordor знала, что в Tudor низкий уровень затрат, она бы не выходила на рынок и тем самым предотвратила бы убыток 29.
Б. Разделяющее равновесие
Если у компании Tudor на самом деле высокий уровень издержек производства, но она хочет, чтобы в Fordor считали, будто он низкий, она должна имитировать действия компании с низкими издержками, то есть установить на свои автомобили цену 15. Но эта цена равна себестоимости единицы продукции, а значит, компания получит нулевую прибыль. Будет ли такая жертва Tudor оправданна? Отпугнет ли она Fordor и обеспечит преимущества монополии в дальнейшем?
Полная игра представлена в экстенсивной форме на рис. 8.7. Обратите внимание, что, как и в , мы используем здесь игрока по имени «природа», для того чтобы выбрать тип издержек Tudor в самом начале игры. Далее Tudor принимает решение о цене. Мы исходим из предположения, что, если в Tudor низкий уровень издержек, она не установит высокую цену. Но если высокий, она может выбрать либо высокую, либо низкую цену, если захочет ввести конкурента в заблуждение. Fordor не может провести различие между двумя ситуациями, в которых Tudor устанавливает низкую цену на автомобили, поэтому варианты выбора Fordor в отношении выхода на рынок, который она делает в этих узлах, объединяются в одно информационное множество. Следовательно, Fordor должна применить в обоих узлах либо стратегию «выйти на рынок», либо «отказаться от выхода на рынок».
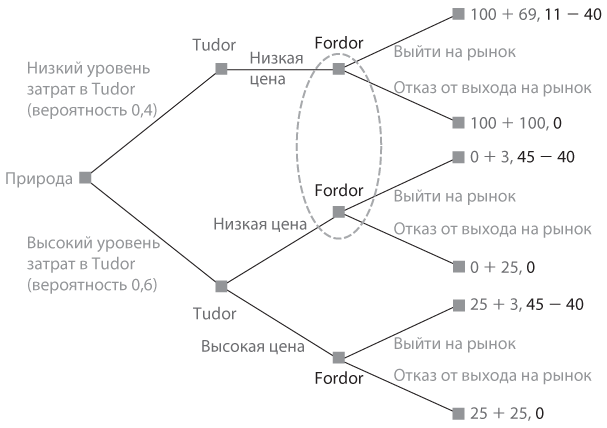
Рис. 8.7. Экстенсивная форма игры «выход на рынок»: низкий уровень издержек в Tudor — 5
В каждом концевом узле первый элемент записи выигрышей (выделено серым цветом) — это прибыль компании Tudor, а второй элемент (выделено черным цветом) — прибыль компании Fordor. Прибыль Tudor суммируется за два периода: первый — когда Tudor — единственный производитель автомобилей данного класса, и второй — когда Tudor может быть либо монополистом, либо участником дуополии в зависимости от решения Fordor о выходе на рынок. Прибыль Fordor охватывает только второй период и отличается от нуля лишь в случае выхода компании на рынок.
Один шаг анализа методом обратных рассуждений позволяет определить, что в нижнем узле, где компания Tudor выбрала высокую цену, Fordor выберет вариант «выйти на рынок», поскольку 45 – 40 + 5 > 0. Следовательно, мы можем отсечь в этом узле ветвь «не выходить на рынок». В результате у каждого игрока остается две стратегии (исчерпывающих плана действий): у Tudor — стратегия «блефовать», или выбрать низкую цену на период 1 независимо от уровня затрат (сокращенно НН в той системе обозначений, о которой шла речь в ), а также «поступить честно», или выбрать низкую цену на протяжении периода 1, если издержки низкие, и высокую цену, если издержки высокие (НВ). У Fordor — стратегия «независимо от обстоятельств», или выйти на рынок независимо от цены, которую установит Tudor на период 1 (сокращенно РР вместо «рынок, рынок»), и «в зависимости от обстоятельств», или выйти на рынок, только если Tudor установит высокую цену на протяжении периода 1 (сокращенно ОР вместо «отказ, рынок»).
Теперь мы можем представить эту игру в стратегической (нормальной) форме. На рис. 8.8 показан каждый игрок с двумя возможными стратегиями; выигрыши в каждой ячейке — ожидаемая прибыль каждой компании, полученная с учетом вероятности (40%) того, что в Tudor низкий уровень издержек. Эти расчеты аналогичны выполненным нами для заполнения таблицы на . Как и тогда, вы можете упростить расчеты, если обозначите концевые узлы дерева игры и определите, какие из них соответствуют каждой ячейке таблицы.

Рис. 8.8. Стратегическая форма игры «выход на рынок»: низкий уровень издержек Tudor — 5
Это простая игра, разрешимая по доминированию. В случае Tudor стратегия «поступить честно» доминирует над стратегией «блефовать». А наилучший ответ Fordor на доминирующую стратегию Tudor «поступить честно» — «в зависимости от обстоятельств». Таким образом, «поступить честно» / «в зависимости от обстоятельств» — единственное равновесие Нэша в этой игре (совершенное равновесие подыгры).
Равновесие, найденное на , будет разделяющим. Для двух типов издержек компания Tudor устанавливает разные цены на период 1. Это действие раскрывает компании Fordor тип Tudor, которая после этого принимает соответствующее решение о выходе на рынок.
Ключ к пониманию того, почему стратегия «поступить честно» для Tudor доминирующая, можно найти в сравнении выигрышей компании в случае стратегии Fordor «в зависимости от обстоятельств». Вот исходы игры, если стратегия Tudor «блефовать» сработает: Fordor выйдет на рынок, если Tudor установит высокую цену на период 1, и откажется от этого, если Tudor установит низкую цену на период 1. Если в Tudor действительно низкий уровень издержек, то ее выигрыши против стратегии Fordor «в зависимости от обстоятельств» одни и те же независимо от того, какую стратегию она применит — «блефовать» или «поступить честно». Однако если в Tudor высокий уровень издержек, результаты будут разниться.
Если Fordor выберет стратегию «в зависимости от обстоятельств», а Tudor — высокие издержки, Tudor может успешно использовать стратегию блефа. Однако успешный блеф обойдется ей слишком дорого. Если бы в Tudor назначили самую выгодную монопольную цену (стратегия «поступить честно») на период 1, компания получила бы прибыль 25; низкая цена при блефе кардинально сокращает размер прибыли на протяжении периода 1, в данном случае до 0. Более высокая монопольная цена в течение периода 1 стимулировала бы выход Fordor на рынок и уменьшила бы прибыль Tudor за период 2 с монопольного уровня 25 до дуопольного уровня 3. Тем не менее выгода Tudor, полученная на протяжении периода 2 за счет установления низкой цены (стратегия «блефовать») и препятствования выходу Fordor на рынок (25 – 3 = 22), меньше издержек, чем в периоде 1, понесенных вследствие блефа и потери монопольной прибыли (25 – 0 = 25). При наличии малейшей положительной вероятности того, что в Tudor высокий уровень издержек, преимущества от выбора стратегии «поступить честно» превзойдут преимущества от стратегии «блефовать», даже если компания Fordor применит стратегию «в зависимости от обстоятельств».
Если бы низкая цена была не настолько низкой, то при наличии высоких издержек Tudor пошла бы на меньшие жертвы, имитируя тип компании с низкими издержками. Ниже мы проанализируем именно эту возможность.
В. Объединяющее равновесие
Давайте представим, что более низкие издержки производства в Tudor составляют 10 на один автомобиль, а не 5. При таком изменении их уровня компания Tudor, в которой на самом деле высокие издержки, по-прежнему заработает прибыль 25 в случае монополии, если изменит цену 20, обеспечивающую максимальную прибыль. Но теперь Tudor как компания с низким уровнем издержек установит цену 17,5 в качестве монополиста (вместо 15) и заработает прибыль 56. Если компания с высоким уровнем издержек будет имитировать их низкий уровень и тоже установит цену 17,5, ее прибыль составит 19, а не 0, как в предыдущем примере; в таком случае потеря прибыли в результате блефа гораздо меньше: 25 − 19 = 6, а не 25. Если Fordor выйдет на рынок, то прибыль двух компаний в их игре в дуополию составит 3 для Tudor и 45 для Fordor, если в Tudor высокий уровень издержек (как в предыдущем разделе). В дуополии прибыль каждой компании теперь равна 25, если в Tudor низкий уровень издержек; в этой ситуации у Fordor и у Tudor с низким уровнем издержек будет одинаковый уровень затрат на единицу продукции в размере 10.
Теперь предположим, что Tudor относится к типу компаний с низким уровнем издержек с вероятностью 40% (0,4), а убеждение Fordor в отношении вероятности низких издержек в Tudor верно. Новое дерево игры изображено на рис. 8.9. Поскольку Fordor все так же выберет вариант «выйти на рынок», если Tudor установит высокую цену, ситуация снова будет сведена к игре, в которой у каждого игрока есть ровно две исчерпывающие стратегии и они те же, что и в . Таблица выигрышей для нормальной формы игры представлена на рис. 8.10.
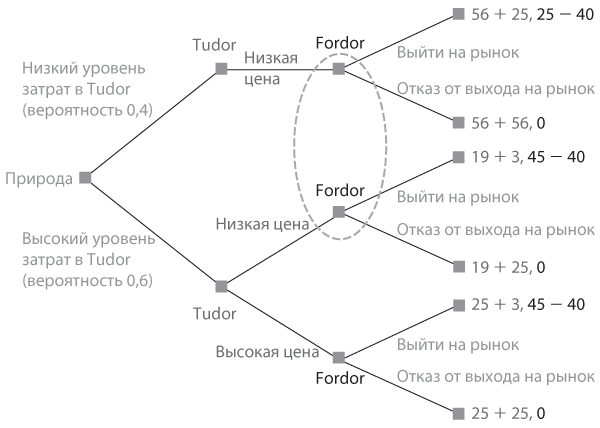
Рис. 8.9. Экстенсивная форма игры «выход на рынок»: в Tudor низкий уровень издержек — 10

Рис. 8.10. Стратегическая форма игры «выход на рынок»: в Tudor низкий уровень издержек — 10
Это еще одна игра, разрешимая по доминированию. Но сейчас доминирующей стратегией располагает компания Fordor: она всегда будет выбирать вариант «в зависимости от обстоятельств». А при условии доминирования стратегии «в зависимости от обстоятельств» Tudor всегда будет выбирать «блефовать». Таким образом, «блефовать» / «в зависимости от обстоятельств» — единственное равновесие Нэша в этой игре (совершенное равновесие подыгры). Во всех остальных ячейках таблицы одна компания может добиться большего, переключившись на другое действие. Мы предоставляем вам возможность подумать над тем, почему каждое такое отклонение выгодно компании.
Равновесие, найденное на , подразумевает объединение. При обоих типах издержек Tudor устанавливает одну и ту же (низкую) цену, а Fordor, видя это, отказывается выходить на рынок. Знание этой цены не дает Fordor никакой информации. По оценке Fordor, вероятность того, что в Tudor низкие издержки производства, остается 0,4; компания определяет ожидаемую прибыль от выхода на рынок в размере −3 < 0, поэтому решает не выходить. Даже если Fordor прекрасно известно, что Tudor блефует в равновесии, риск в связи с раскрытием блефа слишком велик, поскольку вероятность того, что в Tudor действительно низкий уровень затрат, достаточно высока.
Но что если бы эта вероятность была меньше (скажем, 0,1) и Fordor об этом знала? Если все остальные показатели не изменятся, ожидаемая прибыль Fordor от стратегии «независимо от обстоятельств» составит –15 × 0,1 + 5 × 0,9 = 4,5 – 1,5 = 3 > 0. Тогда Fordor выйдет на рынок, какую бы цену ни установила Tudor, и блеф Tudor не возымеет действия. Такая ситуация приводит к формированию нового равновесия, характеристики которого мы рассмотрим ниже.
Г. Полуразделяющее равновесие
Теперь проанализируем исходы игры «выход на рынок» в ситуации, когда вероятность достижения Tudor низкого уровня издержек производства в размере 10 составляет всего 10% (0,1). Все показатели затрат и прибыли те же, что и в предыдущем разделе, изменилась только вероятность. Поэтому мы не приводим здесь повторно дерево игры (), а покажем только таблицу выигрышей (рис. 8.11).

Рис. 8.11. Стратегическая форма игры «выход на рынок»: низкий уровень издержек в Tudor составляет 10 с вероятностью 0,1
В новой ситуации в игре, представленной на рис. 8.11, нет равновесия в чистых стратегиях. С парой стратегий «блефовать» / «независимо от обстоятельств» Tudor выигрывает, переключившись на «поступить честно»; с парой «поступить честно» / «независимо от обстоятельств» Fordor выигрывает, переключившись на «в зависимости от обстоятельств»; с парой «поступить честно» / «в зависимости от обстоятельств» Tudor выигрывает, переключившись на стратегию «блефовать»; с парой «блефовать» / «в зависимости от обстоятельств» Fordor выигрывает, переключившись на «независимо от обстоятельств». Мы снова предоставляем вам возможность самостоятельно поразмышлять над тем, почему каждое из этих отклонений выгодно.
Таким образом, теперь нам нужно искать равновесие в смешанных стратегиях. Предположим, Tudor смешает стратегии «блефовать» и «поступить честно» с вероятностями p и (1 – p) соответственно. Аналогичным образом Fordor смешает стратегии «независимо от обстоятельств» и «в зависимости от обстоятельств» с вероятностями q и (1 – q) соответственно. Выбранная Tudor p-комбинация должна поддерживать безразличие компании Fordor в отношении выбора между ее двумя чистыми стратегиями «независимо от обстоятельств» и «в зависимости от обстоятельств», поэтому нам нужно, чтобы выполнялось равенство
3p + 3(1 – p) = 0p + 4,5(1 – p), или 4,5(1 – p) = 3, или 1 – p = 2/3, или p = 1/3.
В свою очередь, q-комбинация Fordor должна поддерживать безразличие компании Tudor в отношении выбора между ее двумя чистыми стратегиями «блефовать» и «поступить честно», а значит, необходимо выполнение равенства
27,9q + 50,8(1 – q) = 33,3q + 36,4(1 – q), или 5,4q = 14,4(1 – q), или q = 14,4/19,8 = 16/22 = 0,727.
В таком случае равновесие данной игры в смешанных стратегиях сводится к тому, что Tudor будет выбирать стратегию «блефовать» с вероятностью 1/3, а «поступить честно» с вероятностью 2/3, тогда как Fordor будет выбирать «независимо от обстоятельств» с вероятностью 16/22, а «в зависимости от обстоятельств» с вероятностью 6/22.
В этом равновесии типы Tudor разделены лишь частично. Tudor с низким уровнем затрат всегда устанавливает низкую цену на период 1, тогда как Tudor с высоким уровнем затрат смешивает чистые стратегии и устанавливает низкую цену в одной трети случаев. Если Fordor наблюдает высокую цену на протяжении периода 1, она может быть уверена, что Tudor — компания с высоким уровнем издержек, и всегда будет выбирать стратегию выхода на рынок. Но в случае низкой цены Fordor не будет знать, с каким типом Tudor имеет дело — с компанией с действительно низким уровнем издержек или с блефующей компанией, в которой на самом деле высокий уровень затрат. В такой ситуации Fordor также будет придерживаться смешанной стратегии, выбирая выход на рынок в 72,7% случаев. Стало быть, высокая цена передает исчерпывающую информацию, тогда как низкая лишь частично раскрывает информацию о типе Tudor. Именно поэтому равновесие такого типа называется полуразделяющим.
Для того чтобы лучше понять смешанные стратегии каждой компании и полуразделяющее равновесие, проанализируем, как Fordor может применить частичную информацию, которую раскрывает низкая цена, установленная Tudor. Видя низкую цену на протяжении периода 1, Fordor сможет использовать это наблюдение для обновления своего убеждения в отношении вероятности того, что Tudor — компания с низким уровнем издержек; это можно сделать с помощью теоремы Байеса. Таблица расчетов представлена на рис. 8.12; она аналогична таблице на в приложении.
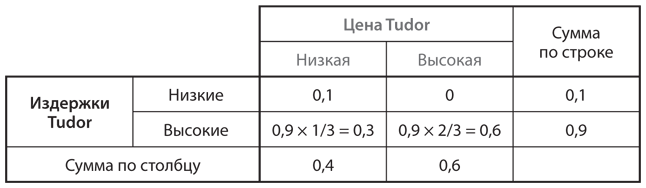
Рис. 8.12. Применение теоремы Байеса в игре «выход на рынок»
В этой таблице возможные типы издержек Tudor приведены в строках, а цены, наблюдаемые Fordor, — в столбцах. Значения в ячейках представляют собой вероятность того, что Tudor типа, указанного в соответствующей строке, выберет цену, указанную в соответствующем столбце (в котором отображены вероятности применения чистых стратегий в равновесной смешанной стратегии Tudor). В последней строке и последнем столбце таблицы отображены общие вероятности каждого типа и наблюдения каждой цены соответственно.
Согласно правилу Байеса, когда Fordor увидит, что Tudor устанавливает низкую цену на период 1, она пересмотрит свое убеждение относительно вероятности того, что в Tudor низкий уровень затрат. Для этого Fordor разделит вероятность того, что Tudor с низким уровнем издержек установит низкую цену (значение 0,1 в верхней левой ячейке), на общую вероятность того, что Tudor для двух типов издержек выберет низкую цену (значение 0,4, сумма по левому столбцу). Эти расчеты позволяют получить скорректированное убеждение Fordor относительно вероятности того, что в Tudor низкий уровень издержек: 0,1/0,4 = 0,25. Затем Fordor также уточнит значение ожидаемой прибыли от выхода на рынок: –15 × 0,25 + 5 × 0,75 = 0. Стало быть, равновесная комбинация Tudor такова, что компании Fordor безразлично, выходить ей на рынок или нет, если она видит низкую цену, установленную Tudor на период 1. Именно такой исход необходим для поддержания стремления Tudor смешивать чистые стратегии в равновесии.
Исходная вероятность 0,1 того, что в Tudor низкий уровень издержек, слишком низкая, чтобы удержать Fordor от выхода на рынок. Пересмотренная вероятность Fordor составляет 0,25 после наблюдения за низкой ценой, установленной Tudor на период 1. Почему? Именно по той причине, что в случае высоких издержек Tudor не всегда блефует. Если бы это было так, то низкая цена не передавала бы никакой информации и тогда пересмотренная вероятность Fordor составляла бы 0,1 и компания приняла бы решение выйти на рынок. Но если Tudor с высоким уровнем издержек блефует лишь иногда, то низкая цена с большей вероятностью свидетельствует о низких издержках.
В игре «выход на рынок» мы определили равновесия интуитивно понятным способом, а теперь вернемся назад и проанализируем их характер более систематически. В каждом конкретном случае мы сначала убеждались, что стратегия каждого игрока (и каждого типа) оптимальна с учетом стратегий остальных игроков, и применяли концепцию равновесия Нэша. Далее удостоверялись, что игроки делают правильные выводы из своих наблюдений; это потребовало вычисления вероятностей с помощью теоремы Байеса, а именно вероятностей в полуразделяющем равновесии. Совокупность концепций, необходимых для идентификации равновесий в таких играх с асимметричной информацией, оправдывает их обозначение термином байесовские равновесия Нэша. И наконец, хотя это и была весьма незначительная часть примера, мы выполнили анализ методом обратных рассуждений, или совершенного равновесия подыгры. Использование обратных рассуждений дает основания назвать данное равновесие совершенным байесовским равновесием. Наш пример содержит все эти концепции равновесия; вы встретитесь с несколько более сложным вариантом некоторых из них в следующих главах, а также в более полном контексте в ходе дальнейшего изучения теории игр.
Резюме
Столкнувшись с несовершенной или неполной информацией, игроки с разным отношением к риску или разным объемом имеющейся информации могут прибегнуть к стратегическим действиям в целях управления и манипулирования риском и информацией в соответствующей игре. Игроки могут уменьшить риск посредством применения различных схем платежей или его разделения с другими, хотя последний способ осложняют такие аспекты, как моральный риск и неблагоприятный отбор. Иногда риском можно манипулировать в пользу игрока в зависимости от сложившихся в игре обстоятельств.
Игроки, владеющие личной информацией, могут захотеть ее скрыть или обнародовать, тогда как игроки, у которых такой информации нет, могут попытаться ее получить или не делать этого. При наличии асимметричной информации дела убедительнее слов. Для того чтобы раскрыть информацию, необходимо подать достоверный сигнал. Когда обычных слов для достоверной передачи информации достаточно, может возникнуть равновесие дешевого разговора; в его достижении важную роль играет степень согласованности интересов игроков. Когда информационное содержание слов игрока не принимается во внимание, в игре наблюдается равновесие пустого разговора.
В более общем смысле информацию передают любые конкретные действия, предпринятые игроками. Сигнализирование обеспечивает требуемый результат, только если сигнальное действие влечет за собой различные издержки для игроков с разной информацией. Когда простой постановки вопросов для получения правдивой информации недостаточно, может понадобиться схема скрининга, предназначенная для обнаружения конкретного действия. Скрининг обеспечивает требуемые результаты, только когда инструмент скрининга стимулирует других игроков раскрыть правдивую информацию о своем типе; разделение типов возможно лишь при наличии совместимости стимулов. Иногда достоверное сигнализирование или скрининг могут оказаться невозможны; в таком случае равновесие может повлечь за собой объединение типов или вероятен полный крах рынка или сделки для одного из типов. Многочисленные примеры сигнализирования и скрининга можно наблюдать в обычных ситуациях, таких как рынок труда или страхование. Фактические данные о способности игроков достигать совершенного байесовского равновесия говорят о том, что, несмотря на трудности вычисления необходимых вероятностей, такие равновесия встречаются достаточно часто. Различные экспериментальные данные, по всей видимости, в значительной мере зависят от схемы проведения эксперимента.
В равновесии игры с асимметричной информацией игроки должны не только использовать свои наилучшие действия с учетом имеющейся информации, но и делать правильные выводы (обновлять информацию) в процессе наблюдения за действиями других игроков. Этот тип равновесия известен как байесовское равновесие Нэша. При необходимости выполнить требование об оптимальности действий во всех узлах (как в ходе анализа методом обратных рассуждений) данное равновесие становится совершенным байесовским равновесием. Исход такой игры может подразумевать объединение, разделение и частичное разделение типов в зависимости от особенностей структуры выигрышей и способов уточнения информации, используемых игроками. В некоторых диапазонах параметров такие игры могут иметь различные типы совершенных байесовских равновесий.
Ключевые термины
Байесовское равновесие Нэша
Инструмент скрининга
Моральный риск
Неблагоприятный отбор
Объединение типов
Ограничения совместимости стимулов
Отрицательная корреляция
Положительная корреляция
Полуразделяющее равновесие
Равновесие дешевого разговора
Равновесие пустого разговора
Разделение типов
Самоотбор
Сигнал
Сигнализирование
Скрининг
Совершенное байесовское равновесие
Совместимость стимулов
Типы игроков
Условия совместимости стимулов
Условия участия
Частично раскрывающее равновесие
Упражнения с решениями
S1. В примере с торговлей рисками из у вас был рискованный доход в сумме 160 000 долларов в случае удачи (вероятность 0,5) и 40 000 долларов в случае неудачи (вероятность 0,5). При наличии у вашего приятеля гарантированного дохода 100 000 долларов мы вывели схему, в соответствии с которой вы могли устранить весь свой риск и в то же время немного повысить ожидаемую полезность для приятеля. Предположим, для каждого из вас полезность по-прежнему равна квадратному корню из соответствующего дохода. Однако теперь пусть вероятность удачи составляет 0,6. Придумайте контракт, который позволит вам получить доход в размере 100 000 долларов, когда вас постигнет неудача. Пусть x — это сумма, которую вы выплатите при этом приятелю.
a) При каком минимальном значении x (с точностью до цента) ваш приятель отдаст хотя бы малейшее предпочтение заключению контракта его полному отсутствию?
b) При каком максимальном значении x (с точностью до цента) такой контракт обеспечит вам чуть более высокую ожидаемую полезность, чем его полное отсутствие?
S2. Местная благотворительная организация получила пожертвование на бесплатные обеды для бездомных в своем городе, но ее руководство обеспокоено тем, что этой программой могут воспользоваться студенты близлежащего колледжа, которые не прочь бесплатно поесть. И бездомный, и студент получают за бесплатную еду выигрыш 10. Издержки в связи с необходимостью стоять в очереди за обедом составляют t2/320 для бездомного и t2/160 для студента, где t — количество времени (в минутах), проведенного в очереди. Предположим, сотрудники благотворительной организации не могут определить истинный тип тех, кто приходит бесплатно поесть.
a) При каком минимальном значении времени ожидания t будет достигнуто разделение типов?
b) Через какое-то время сотрудники благотворительной организации уже могут успешно идентифицировать студентов и отказать им в обеде в половине случаев. Студенты, получившие отказ, несут дополнительные издержки в размере 5 в связи с потерей времени в очереди и испытанным стыдом. Уменьшит или увеличит частичная идентификация студентов колледжа ответ, полученный в пункте а? Обоснуйте свой вывод.
S3. Рассмотрим рынок подержанных автомобилей марки Citrus 2011 года, о котором шла речь в . Теперь спрос на них резко вырос, и покупатели готовы выложить 18 000 за «апельсин» и 8000 за «лимон». Все остальные показатели те же, что и в примере в .
a) Какую цену покупатели были бы готовы заплатить на Citrus 2011 года неизвестного типа, если бы доля «апельсинов» f в общей совокупности подержанных автомобилей Citrus составила 0,6?
b) Сформируется ли рынок «апельсинов» при f = 0,6? Обоснуйте свой ответ.
c) Какую цену покупатели были бы готовы заплатить, если бы значение f равнялось 0,2?
d) Сформируется ли рынок «апельсинов» при f = 0,2? Обоснуйте ответ.
e) При каком минимальном значении f рынок «апельсинов» не рухнет?
f) Объясните, почему повышение готовности покупателей платить приводит к изменению порогового значения f, при котором наступает крах рынка «апельсинов».
S4. Представим, что электрики бывают двух типов: компетентные и некомпетентные. Оба типа электриков могут получить сертификаты, но некомпетентным электрикам для этого понадобится больше времени и усилий. Компетентным электрикам нужно С месяцев, чтобы подготовиться к экзамену на получение сертификата; некомпетентным — в два раза больше. Сертифицированные электрики могут зарабатывать 100 (тысяч долларов) в год, работая на строительных площадках лицензированных подрядчиков. Электрики без сертификата могут зарабатывать только 25 (тысяч долларов) в год, работая на себя (лицензированные подрядчики их не наймут). Каждый тип электрика получает выигрыш, равный √S – M, где S — заработная плата, выраженная в тысячах долларов, а M — количество месяцев, потраченных на получение сертификата. При каком диапазоне значений C компетентный электрик примет решение подать сигнал посредством этого инструмента, тогда как некомпетентный решит этого не делать?
S5. Вернемся к примеру с компаниями Tudor и Fordor из , когда издержки Tudor на единицу продукции составляют 5. Пусть z — вероятность того, что в Tudor действительно низкий уровень затрат на единицу продукции.
a) Перепишите таблицу на с учетом значения z.
b) Сколько равновесий в чистых стратегиях существует при z = 0? Обоснуйте ответ.
c) Сколько равновесий в чистых стратегиях существует при z = 1? Обоснуйте ответ.
d) Докажите, что равновесие Нэша в этой игре — это разделяющее равновесие при любом значении z в диапазоне от 0 до 1 (включительно).
S6. Опять же, вернувшись к примеру с Tudor и Fordor, предположим, что старая, авторитетная компания Tudor не расположена к риску, тогда как потенциальный участник рынка Fordor (планирующий финансировать свой проект за счет венчурного капитала) относится к нему нейтрально. Иными словами, полезность для Tudor неизменно равна квадратному корню из общей прибыли за оба периода. Полезность в случае Fordor — просто объем прибыли (если она есть), полученной за второй период. Допустим, издержки Tudor на единицу продукции составляют 5, как и в .
a) Представьте игру в экстенсивной форме (как показано на ), указав соответствующие выигрыши для компании Tudor, не расположенной к риску.
b) Пусть вероятность z того, что Tudor — компания с низким уровнем издержек, составляет 0,4. Будет ли равновесие в такой игре разделяющим, объединяющим или полуразделяющим? (Подсказка: используйте таблицу, эквивалентную представленной на .)
c) Выполните задание пункта b при z = 0,1.
S7. Вернемся к ситуации, в которой компания Tudor нейтральна к риску, но с низкими затратами на единицу продукции, равными 6 (вместо 5 или 10, как в ). Если в Tudor низкий уровень издержек, то компания заработает 90 в рамках монополии, обеспечивающей максимальную прибыль. Если Fordor выйдет на рынок, Tudor заработает 59 в рамках сформировавшейся дуополии, тогда как Fordor — 13. Если в Tudor на самом деле высокий уровень издержек (то есть затраты на единицу продукции составляют 15), а цены установлены на таком уровне, как если бы он был низкий (издержки на единицу продукции составляют 6), то в случае монополии она заработает 5.
a) Нарисуйте дерево этой игры, эквивалентное представленному на или , изменив соответствующие выигрыши.
b) Составьте нормальную форму этой игры исходя из предположения, что вероятность низкой цены в Tudor равна 0,4.
c) Найдите равновесие игры. Оно разделяющее, объединяющее или полуразделяющее? Обоснуйте свой ответ.
S8. Феликс и Оскар играют в упрощенную версию покера. Каждый делает начальную ставку в размере 8 долларов. Затем каждый по отдельности тянет карту, которая с равной вероятностью может оказаться старшей или младшей. Каждый видит свою карту, но не видит карты соперника.
Далее Феликс решает, какое действие выбрать — «выйти из игры» или «поднять ставку» (добавить в банк 4 доллара). Если «выйти из игры», обе карты открываются и сравниваются. Если карты разные, то игрок со старшей картой забирает весь банк. В банке 16 долларов, из которых 8 долларов внес сам победитель, то есть его чистый выигрыш 8 долларов. Выигрыш проигравшего равен −8 долларам. Если карты одинаковые, банк делится поровну и каждый игрок получает свои 8 долларов (выигрыш 0) назад.
Если Феликс сыграет «повысить ставку», Оскару необходимо решить, какое действие выбрать — «сбросить карту» (сдаться) или «раскрыть карту» (добавить в банк сумму в 4 доллара). Если «сбросить карту», то Феликс забирает весь банк независимо от того, какие у него карты. Если «раскрыть карту», то карты открываются и сравниваются. Процедура та же, что описана в предыдущем абзаце, только теперь в банке больше денег.
a) Представьте эту игру в экстенсивной форме (будьте внимательны с информационными множествами).
Если отобразить эту игру в нормальной форме, в распоряжении Феликса есть четыре стратегии: 1) «выйти из игры» в любом случае (сокращенно ВВ); 2) «поднять ставку» в любом случае (ПП); 3) «поднять ставку», если своя карта старшая, и «выйти из игры», если своя карта младшая (ПВ); 4) наоборот (ВП). В распоряжении Оскара тоже четыре стратегии: 1) «сбросить карту» в любом случае (СС); 2) «раскрыть карту» в любом случае (РР); 3) «раскрыть карту», если своя карта старшая, и «сбросить карту», если своя карта младшая (РС); 4) наоборот (СР).
b) Покажите, что таблица выигрышей Феликса выглядит следующим образом.
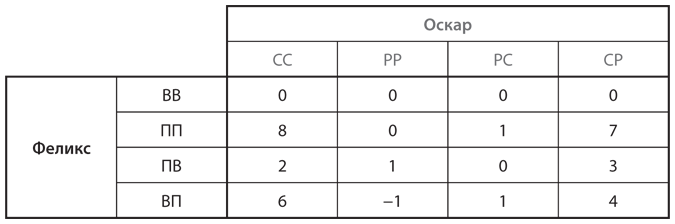
(В каждом случае вам необходимо определить ожидаемое значение посредством вычисления средних результатов по каждой из четырех возможных комбинаций вытягивания карт.)
a) Исключите как можно больше доминируемых стратегий. Найдите в оставшейся таблице равновесие в смешанных стратегиях, а также определите в нем ожидаемый выигрыш Феликса.
b) Основываясь на своих знаниях теории сигнализирования и скрининга, дайте интуитивное объяснение того, почему в этом равновесии присутствуют смешанные стратегии.
S9. Феликс и Оскар играют в другую версию упрощенного покера и делают начальную ставку в один доллар. Феликс (и только Феликс) тянет одну карту, которая с равной вероятностью может оказаться либо королем, либо дамой (всего есть четыре короля и четыре дамы). У Феликса есть выбор: либо «сбросить карту», либо «сделать ставку». Если он выберет «сбросить карту», игра закончится и Оскар получит доллар Феликса в дополнение к своему доллару. Если Феликс сыграет «сделать ставку», он вносит в банк еще один доллар и уже Оскар решает, что делать: «сбросить карту» или «ответить».
Если Оскар выберет «сбросить карту», Феликс выигрывает банк (в котором начальная ставка Оскара один доллар и два доллара Феликса). Если Оскар выберет «ответить», он вносит в банк еще один доллар в ответ на ставку Феликса, а Феликс открывает карту. Если это король, Феликс выигрывает банк (в котором по два доллара с каждого игрока). Если дама, банк выигрывает Оскар.
a) Представьте эту игру в экстенсивной форме (будьте внимательны с информационными множествами).
b) Сколько стратегий в распоряжении каждого игрока?
c) Представьте эту игру в стратегической форме, где указанные в каждой ячейке выигрыши — это ожидаемые выигрыши с учетом соответствующей стратегии каждого игрока.
d) Исключите доминируемые стратегии, если они есть. Найдите равновесие в смешанных стратегиях. Определите в нем ожидаемый выигрыш Феликса.
S10. Ванда работает официанткой и, соответственно, имеет возможность получать чаевые наличными, о которых ее работодатель не отчитывается перед налоговым управлением. Но доход Ванды от чаевых нестабильный. В хороший год (Х) он высокий, поэтому сумма налога, который она должна выплатить, равна 5000 долларов. В плохой год (П) — низкий, и обязательства Ванды перед налоговым управлением составляют 0 долларов. Налоговое управление знает, что вероятность хорошего года у Ванды равна 0,6, а вероятность плохого — 0,4, но ему неизвестно, как именно сложился у нее текущий налоговый год.
В этой игре Ванда сперва решает, о какой сумме дохода отчитаться перед налоговым управлением. Если она сообщит о получении высокого дохода (В), то заплатит налоговому управлению 5000 долларов, если о низком, то 0 долларов. Налоговое управление, в свою очередь, должно решить, проводить ли аудит доходов Ванды. В случае высокого дохода в нем нет необходимости, поскольку налоговое управление автоматически узнает о выплате Вандой соответствующего налога. Если же доход низкий, то налоговое управление может либо провести (А), либо не проводить (Н) аудит. Процедура аудита обходится налоговому управлению в 1000 долларов административных издержек, а Ванде — в 1000 долларов альтернативных издержек в связи с потраченным временем на сбор банковских выписок и встречи с аудитором. Если налоговое управление проводит аудит в плохой год (П), Ванда не должна выплачивать никаких налогов, хотя и она, и налоговое управление несут издержки по 1000 долларов в связи с данной процедурой. Если налоговое управление проводит аудит в хороший год (Х), Ванде придется выплатить 5000 долларов, которые она должна налоговому управлению, помимо издержек, которые она и налоговое управление понесут вследствие аудита.
a) Представим, что у Ванды был хороший год (Х), но она отчитывается в получении низкого дохода (Н). Предположим также, что налоговое управление проводит налоговый аудит (А). Определите общий выигрыш Ванды и общий выигрыш налогового управления.
b) У кого из участников игры есть стимул блефовать (то есть подавать ложный сигнал)? К чему будет сводиться этот блеф?
c) Представьте эту игру в экстенсивной форме (будьте внимательны с информационными множествами).
d) Сколько чистых стратегий есть в распоряжении каждого игрока в этой игре? Обоснуйте свой ответ.
e) Составьте матрицу игры в стратегической форме. Найдите все равновесия Нэша в этой игре. Определите, являются ли они разделяющими, объединяющими или полуразделяющими.
f) Пусть x — вероятность того, что у Ванды хороший год. В исходной версии игры x = 0,6. Найдите такое значение x, при котором Ванда всегда будет сообщать о низком доходе в случае равновесия.
g) Определите весь диапазон значений x, при которых Ванда всегда будет сообщать о низком доходе в случае равновесия.
S11. Структура системы здравоохранения включает несколько аспектов, касающихся вопросов информации и стратегии. Потребители медицинских услуг (потенциальные и фактические пациенты) располагают более полной информацией о состоянии своего здоровья, образе жизни и т. д., чем могут выяснить страховые компании. Поставщики медицинских услуг (врачи, больницы и пр.) знают о потребностях пациентов больше, чем сами пациенты или страховые компании. Кроме того, врачи больше знают о собственной квалификации и затратах труда, а больницы — о своей материальной базе. Страховые компании могут владеть определенным объемом статистической информации о результатах лечения или хирургических процедурах, полученной на основании данных за прошедший период. Но результаты зависят от множества ненаблюдаемых, случайных факторов, поэтому правильные выводы об уровне квалификации, затратах труда или материальной базе не могут быть сделаны только исходя из наблюдений. Фармацевтические компании больше других знают об эффективности лекарственных препаратов. Как правило, у всех этих игроков нет естественных стимулов делиться с другими полной или точной информацией. В процессе разработки данной схемы необходимо попытаться рассмотреть все эти вопросы и найти наиболее приемлемые решения.
Проанализируйте с этой точки зрения сравнительные преимущества различных схем оплаты: оплата за предоставленные услуги или выплата гонораров врачам, комплексные премии за год или оплата каждого визита к пациентам и т. д. Какие схемы наиболее выгодны для потребителей медицинских услуг? А для поставщиков медицинских услуг? Проанализируйте также сравнительные преимущества индивидуального страхования и покрытия расходов за счет общих налоговых поступлений.
S12. В телевизионном рекламном ролике известной торговой марки растворимого капучино мужчина принимает подругу у себя в квартире. Он хочет произвести на нее впечатление и предлагает кофе с десертом. Когда дама принимает предложение, мужчина идет на кухню готовить растворимый капучино и одновременно двигает ящики, выбрасывает что-то в мусорную корзину и т. д., чтобы создать такие звуки, как будто их издает первоклассная (и дорогая) кофемашина. Пока он делает все это, из комнаты слышится голос: «Я хочу увидеть эту машину…»
Используйте свои знания игр с асимметричной информацией, чтобы прокомментировать действия этой пары. Обратите внимание на их попытки применить сигнализирование и скрининг и укажите на конкретные примеры каждой стратегии. Выскажите свое мнение по поводу того, кто из участников этой игры лучший стратег.
S13 (дополнительное упражнение; необходимо ознакомиться с приложением). В примере с генетическим тестом предположим, что тест дает отрицательный результат (наблюдается последствие Y). Какова вероятность того, что у этого человека нет дефекта (что соответствует событию B)? Вычислите ее с помощью правила Байеса, а затем проверьте ответ, выполнив перебор 10 000 членов данной совокупности.
S14 (дополнительное упражнение; необходимо ознакомиться с приложением). Вернемся к примеру с автомобилями марки Citrus 2011 года из . У покупателя нет возможности по внешнему виду отличить надежные «апельсины» от незадачливых «лимонов». В этом примере, если доля «апельсинов» f в общей совокупности подержанных автомобилей Citrus меньше 0,65, продавец «апельсина» не захочет с ним расставаться за максимальную цену, которую готовы заплатить покупатели, поэтому рынок «апельсинов» обвалится.
Но что если у продавца есть дорогостоящий способ сигнализировать о типе автомобиля? Хотя «апельсины» и «лимоны» почти во всех отношениях идентичны, ключевое различие между ними — это то, что «лимон» ломается гораздо чаще. Зная об этом, владельцы «апельсинов» могут сделать следующее предложение. По запросу покупателя продавец за один день совершит на автомобиле поездку туда и обратно на расстояние 500 миль. (Предположим, это можно проверить по показаниям спидометра и по квитанции с временной меткой, полученной на заправочной станции, расположенной в 250 милях.) Для продавцов автомобилей Citrus обоих типов затраты на эту поездку (с учетом расходов на бензин и потраченное время) составляют 0,50 доллара на одну милю (то есть 250 долларов на поездку длиной в 500 миль). Однако «лимон» в ходе такой поездки выйдет из строя с вероятностью q. Если автомобиль сломается, затраты составят 2 доллара на милю общей длины пути, который он попытался преодолеть (то есть 1000 долларов). Кроме того, поломка автомобиля будет верным признаком того, что это «лимон», поэтому он будет продан всего за 6000 долларов.
Допустим, доля «апельсинов» f в общей совокупности подержанных автомобилей Citrus составляет 0,6, вероятность поломки «лимона» q равна 0,5, а владельцы «лимонов» нейтрально относятся к риску.
a) С помощью теоремы Байеса определите значение fуточ. — долю автомобилей Citrus, успешно преодолевших 500 миль и оказавшихся «апельсинами». Предположим, владельцы всех автомобилей Citrus предпримут такую поездку. Значение fуточ. больше или меньше f? Обоснуйте свой ответ.
b) Используйте fуточ. для определения цены pуточ., которую покупатели готовы заплатить за автомобиль Citrus, успешно проехавший 500 миль.
c) Владелец «апельсина» согласится совершить такую поездку и продать автомобиль по цене pуточ.? Почему да или почему нет?
d) Чему равен ожидаемый выигрыш продавца «лимона» от попытки совершить такую поездку?
e) Как бы вы описали исход данного рынка — как объединяющий, разделяющий или полуразделяющий? Обоснуйте свой вывод.
Упражнения без решений
U1. Джек — талантливый инвестор, но его доходы существенно варьируются год от года. В следующем году он рассчитывает заработать 250 000 долларов, если ему повезет, и 90 000 долларов в случае неудачи. Возможно, это несколько странно для человека с такой профессией, но Джек не расположен к риску, поэтому полезность его доходов равна квадратному корню из полученного дохода. Вероятность того, что Джеку улыбнется удача, составляет 0,5.
a) Какова ожидаемая полезность дохода Джека в следующем году?
b) Какая сумма верного дохода обеспечила бы такой же уровень полезности для Джека, что и ожидаемая полезность в пункте а?
Джек встречает Дженет, чья ситуация во всех отношениях совпадает с его. Дженет тоже инвестор и заработает в следующем году 250 000 долларов, если ей повезет, и 90 000 долларов в случае неудачи; она не расположена к риску, поэтому полезность ее дохода равна квадратному корню из суммы дохода, а вероятность того, что ей будет сопутствовать удача, составляет 0,5. Крайне важно, что Джек и Дженет инвестируют таким образом, что их везение носит совершенно независимый характер. Они договариваются о следующей сделке и вне зависимости от того, кому повезет, всегда будут объединять свои доходы, а затем делить их поровну.
c) Перечислите четыре возможные пары удачных исходов и определите вероятность достижения каждого из них.
d) Какова ожидаемая полезность дохода для Джека или Дженет в рамках их договоренности?
e) Какая сумма верного дохода обеспечила бы тот же уровень полезности для Джека и Дженет, что и ожидаемая полезность, полученная в пункте d?
Как бы невероятно это ни звучало, но Джек и Дженет знакомятся с Крисси, ситуация которой аналогична их ситуации в плане дохода, полезности и удачи. Вероятность того, что Крисси повезет, не зависит от удачи Джека и Дженет. После небольшого обсуждения они решают, что Крисси следует присоединиться к соглашению между Джеком и Дженет, согласно которому все трое будут объединять свои доходы и делить их на три равные части.
f) Перечислите восемь возможных троек удачных исходов и определите вероятность достижения каждого из них.
g) Какова ожидаемая полезность дохода для каждого из инвесторов в рамках их расширенной договоренности?
h) Какая сумма верного дохода обеспечила бы всем троим не расположенным к риску инвесторам тот же уровень полезности, что и ожидаемая полезность, полученная в пункте g?
U2. Снова рассмотрим пример с подержанными автомобилями Citrus 2011 года. Почти все автомобили со временем обесцениваются, то же касается и Citrus. По истечении каждого месяца все продавцы (независимо от типа автомобиля) готовы сбросить цену на 100 долларов, а покупатели, в свою очередь, готовы заплатить за «апельсин» максимальную цену на 400 долларов меньше, а за «лимон» — на 200 долларов меньше. Предположим, события в исходном примере происходят на протяжении месяца 0. Восемьдесят процентов автомобилей Citrus — «апельсины», и эта доля не меняется.
a) Заполните три варианта следующей таблицы для месяца 1, месяца 2 и месяца 3:
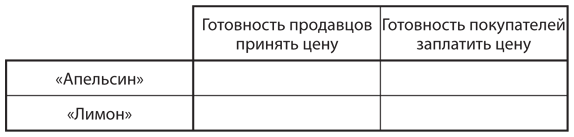
b) Постройте график готовности продавцов «апельсинов» принять максимальную цену покупателей на протяжении следующих 12 месяцев. На том же рисунке постройте график цен, которые готовы платить покупатели за подержанный автомобиль Citrus неизвестного типа (с учетом того, что доля «апельсинов» составляет 80%). (Подсказка: на вертикальной оси отложите значения от 10 000 до 14 000.)
c) Существует ли рынок сбыта «апельсинов» на протяжении месяца 3? Почему да или почему нет?
d) В каком месяце произойдет обвал рынка «апельсинов»?
e) Если бы владельцы «лимонов» не сталкивались с их обесцениванием (то есть никогда бы не соглашались принять цену меньше 3000 долларов), это повлияло бы на момент обвала рынка «апельсинов»? Почему да или почему нет? В каком месяце рухнул бы рынок «апельсинов» в таком случае?
f) Если бы покупатели «лимонов» не сталкивались с их обесцениванием (то есть всегда были бы готовы заплатить за «лимон» до 6000 долларов), это повлияло бы на момент обвала рынка «апельсинов»? Почему да или почему нет? В каком месяце рухнул бы тогда рынок «апельсинов»?
U3. В экономике есть два типа работы — хорошая и плохая, а также два типа работников — квалифицированные и неквалифицированные. Общая совокупность состоит из 60% квалифицированных и 40% неквалифицированных работников. На плохой работе работник любого типа производит 10 единиц продукции. На хорошей квалифицированный работник производит 100 единиц продукции, а неквалифицированный — 0 единиц. Спрос на работников достаточно высокий, п оэтому в случае каждого типа работы компании должны оплачивать труд работников в объеме, соответствующем ожидаемому.
Компаниям приходится нанимать каждого работника, не имея данных о его типе и оплачивая его труд до того, как станет известна его фактическая производительность. Однако квалифицированные работники могут подать сигнал о своей квалификации, получив образование. Для квалифицированного работника затраты на повышение образования до уровня n составляют n2 / 2, тогда как для неквалифицированного n2. Эти издержки исчисляются в тех же единицах, что и объем выпущенной продукции, поэтому n должно быть целым числом.
a) При каком минимальном значении n будет достигнуто разделение типов?
b) Предположим, такой сигнал невозможен. Какие рабочие места будут заполнены работниками каких типов и при какой заработной плате? Кто выиграет и кто проиграет в данной ситуации?
U4. Будучи деканом одного из факультетов Университета Сент-Энфорд, вы нанимаете старших преподавателей с семилетним испытательным сроком, после которого рассматривается вопрос о заключении с ними бессрочного контракта и их либо повышают и зачисляют в штат на постоянной основе, либо увольняют.
Существует два типа старших преподавателей — хорошие и блестящие. Преподаватели, тип которых ниже хорошего, уже отсеяны в процессе найма, но у вас нет возможности непосредственно провести различие между хорошими и блестящими преподавателями. Каждый отдельный преподаватель, безусловно, знает, к какому типу он относится. Вы бы хотели заключить бессрочный контракт только с блестящими преподавателями. Если преподаватель зачислен в штат Университета Сент-Энфорд на постоянной основе, его выигрыш составляет 2 миллиона долларов; эта сумма включает в себя ожидаемую дисконтированную текущую стоимость заработной платы, гонорары за консультации и авторские гонорары за публикацию книг плюс денежный эквивалент чувства гордости и радости, испытываемых преподавателем и членами его семьи в случае получения пожизненной должности в Университете Сент-Энфорд. Тот преподаватель, кому будет отказано в заключении бессрочного контракта, получит должность в Колледже Бундокса; текущая стоимость такой карьеры составляет 0,5 миллиона долларов.
Ваши преподаватели могут проводить научные исследования и публиковать их результаты. Но каждая такая публикация требует усилий и времени, а также порождает напряженность в семье. Все это обходится преподавателю достаточно дорого. Денежный эквивалент таких издержек составляет 30 000 долларов на одну публикацию для блестящего преподавателя и 60 000 долларов для хорошего преподавателя. Вы можете установить минимальное количество публикаций N, которое преподаватель должен предоставить, чтобы получить бессрочный контракт.
a) Не выполняя никаких математических вычислений, максимально подробно опишите, что произошло бы в случае полуразделяющего равновесия в данной игре.
b) Существует два возможных типа объединяющих исходов в данной игре. Не выполняя никаких математических вычислений, как можно подробнее опишите, как бы выглядели эти исходы.
c) А теперь предлагаем выполнить некоторые математические вычисления. Найдите множество возможных значений N, при которых вы достигли бы своей цели — отличить блестящих профессоров от просто хороших.
U5. Вернитесь к задаче с компаниями Tudor и Fordor из , где низкий уровень затрат Tudor на единицу продукции составляет 10. Пусть z — вероятность того, что в Tudor действительно низкие издержки на единицу продукции.
a) Перепишите таблицу на с учетом значения z.
b) Сколько равновесий в чистых стратегиях существует при z = 0? Какой тип равновесия (разделяющее, объединяющее или полуразделяющее) наблюдается при z = 0? Обоснуйте свой ответ.
c) Сколько равновесий в чистых стратегиях существует при z = 1? Какой тип равновесия (разделяющее, объединяющее или полуразделяющее) наблюдается при z = 1? Обоснуйте свой ответ.
d) При каком минимальном значении z существует объединяющее равновесие?
e) Объясните на интуитивном уровне, почему объединяющее равновесие не может существовать при слишком низком значении z.
U6. Предположим, компания Tudor не расположена к риску и в ее случае полезность равна квадратному корню из общей прибыли (см. ), а компания Fordor нейтральна к риску. Кроме того, допустим, что низкий уровень издержек Tudor на единицу продукции составляет 10, как в .
a) Представьте игру в экстенсивной форме (как показано на ), указав соответствующие выигрыши для компании Tudor, не расположенной к риску.
b) Пусть вероятность z того, что Tudor — компания с низким уровнем издержек, составляет 0,4. Будет ли равновесие в такой игре разделяющим, объединяющим или полуразделяющим? (Подсказка: используйте таблицу, эквивалентную представленной на .)
c) Выполните задание пункта а при z = 0,1.
d) (дополнительное задание). Изменит ли нерасположенность Tudor к риску ответ, полученный в ? Объясните, почему да или почему нет.
U7. Вернитесь к ситуации в , в которой компания Tudor нейтральна к риску, а ее низкий уровень издержек на единицу продукции составляет 6.
a) Составьте нормальную форму этой игры с учетом значения z, то есть вероятности того, что Tudor установит низкую цену.
b) Найдите равновесие игры при z = 0,1. Это разделяющее, объединяющее или полуразделяющее равновесие?
c) Выполните задание пункта b при z = 0,2,
d) Выполните задание пункта b при z = 0,3.
e) Сравните ответы, полученные в пунктах b, c и d, с ответом в . Когда низкий уровень издержек Tudor 6 вместо 10, можно ли достичь объединяющего равновесия при более низких значениях z? Или для объединяющих равновесий требуются более высокие значения z? Объясните на интуитивном уровне, почему это действительно так.
U8. Иногда корпоративные судебные споры могут выступать в качестве сигнальных игр. Вот один пример. В 2003 году компания AT&T подала иск против компании eBay, утверждая, что ее электронные платежные системы Billpoint и PayPal нарушают оформленный в 1994 году патент AT&T на «посредничество в проведении транзакций с помощью системы связи».
Проанализируем эту ситуацию с момента подачи иска. В ответ на этот иск, как и в случае большинства исков о нарушении патентных прав, eBay может предложить AT&T урегулировать ситуацию без обращения в суд. Если AT&T примет предложение eBay, судебного разбирательства не будет; если отклонит, результат определит суд.
Сумма убытков, заявленная AT&T, не подлежит огласке. Поэтому предположим, что AT&T подает иск на сумму 300 миллионов долларов. Кроме того, допустим, что, если дело дойдет до судебного разбирательства, обе стороны понесут судебные издержки (на оплату услуг адвокатов и консультантов) в размере 10 миллионов каждая.
Поскольку eBay действительно занимается бизнесом, связанным с обработкой электронных платежей, она наверняка больше AT&T знает о том, какова ее вероятность выиграть это дело в суде. Для простоты давайте исходить из того, что eBay точно известно, признают ли ее невиновной (н) или виновной (в) в нарушении патентных прав. С точки зрения AT&T, вероятность того, что eBay виновна (в) составляет 25%, а невиновна (н) — 75%.
Допустим, в распоряжении eBay есть два возможных действия: щедрое предложение об урегулировании претензий (Щ) в размере 200 миллионов долларов или скупое предложение об урегулировании претензий (С) в размере 20 миллионов долларов. Если eBay сделает щедрое предложение, AT&T примет его и тем самым избежит дорогостоящего судебного разбирательства. Если eBay сделает скупое предложение, то AT&T предстоит решить, принять его (П) и избежать судебного разбирательства или отклонить (О) и отправить дело в суд. Если в ходе судебного разбирательства компанию eBay признают виновной, помимо оплаты судебных издержек ей придется выплатить AT&T 300 миллионов долларов. Если eBay признают невиновной, она не должна AT&T ничего, зато AT&T придется оплатить все судебные издержки.
a) Представьте эту игру в экстенсивной форме (правильно обозначьте информационные множества).
b) У кого из участников игры есть стимул блефовать (другими словами, подавать ложный сигнал)? В чем будет состоять этот блеф? Объясните логику своих рассуждений.
c) Представьте игру в стратегической форме (составьте таблицу игры) Найдите в этой игре все равновесия Нэша. Вычислите ожидаемые выигрыши каждого игрока в случае равновесия.
U9. Вернемся к игре в упрощенный покер между Феликсом и Оскаром из . Каким должно быть соотношение королей и дам, чтобы игра была справедливой? Иными словами, какая доля королей сделает ожидаемый выигрыш равным нулю для обоих игроков?
U10. Феликсу и Оскару наскучила упрощенная версия покера, поэтому они решили сделать ее более интересной, добавив в игру третью карту — валет. Теперь помимо четырех королей и четырех дам в колоде есть еще и четыре валета. Все правила игры остаются прежними, за одним исключением — последствиями ситуации, когда Феликс делает ставку, а Оскар отвечает. При таком раскладе Феликс выигрывает банк, если у него есть король, оба игрока «сравнивают счет» и каждый получает свои деньги обратно, если у Феликса дама, и Оскар выигрывает банк, если эта карта — валет.
a) Представьте игру в экстенсивной форме (правильно обозначьте информационные множества).
b) Сколько чистых стратегий у Феликса в этой игре? Объясните логику своих рассуждений.
c) Сколько чистых стратегий в этой игре у Оскара? Объясните логику своих рассуждений.
d) Представьте игру в стратегической форме. Это должна быть таблица ожидаемых выигрышей каждого игрока в случае той или иной пары стратегий.
e) Найдите единственное равновесие Нэша в чистых стратегиях в этой игре.
f) Можно ли назвать его объединяющим, разделяющим или полуразделяющим?
g) В случае равновесия чему равен ожидаемый выигрыш Феликса в этой игре? Действительно ли это честная игра?
U11. Рассмотрим модель сигнализирования на рынке труда (модель Спенса) со следующими уточнениями. Существуют два типа работников — 1 и 2. Производительность их труда определяется как функции уровня образования E:
W1(E) = E; W2(E) = 1,5E.
Затраты на образование двух типов работников как функции уровня образования составляют
C1(E) = E2/2; C2(E) = E2/3.
Полезность каждого работника равна его доходу минус затраты на образование. Компании, которые пытаются их нанять, поддерживают совершенную конкуренцию на рынке труда.
a) Если информация о типах работников открыта для ознакомления (то есть поддается наблюдению и проверке), найдите выражения для уровней образования, доходов и полезности двух типов работников.
Теперь предположим, что тип работника — это его личная информация.
b) Убедитесь в том, что если в данной ситуации с асимметричностью информации будет предпринята попытка заключить контракты, то тип 2 не захочет получить контракт, предназначенный для типа 1, а тип 1 захочет получить контракт, предназначенный для типа 2; следовательно, «естественное» разделение типов не может преобладать.
c) Если оставить контракт для типа 1 как в пункте а, при каком диапазоне контрактов (пар «образование / заработная плата») для типа 2 может быть достигнуто разделение?
d) Какой, по вашему мнению, из всех возможных разделяющих контрактов получит приоритет?
e) Кто выиграет или проиграет из-за асимметричности информации? В какой степени?
U12. «Господин Робинсон фактически приходит к выводу, что бизнес-школы — это своего рода инструменты отсева: степень MBA есть не что иное, как профсоюзный билет для яппи. Но, пожалуй, самый важный факт о Стэнфордской школе бизнеса состоит в том, что весь серьезный отсев происходит еще до начала первого занятия. В стенах учебного заведения не проводится грязная работа по прополке сорняков. “Они не хотят тебя проваливать. Они хотят, чтобы после выпуска ты со временем разбогател и пожертвовал своей альма-матер кучу денег”. Однако здесь возникает вопрос: если компании перекладывают на приемную комиссию Стэнфордской школы бизнеса ответственность за подбор молодых менеджеров, почему бы им просто не заменить сотрудников своего отдела управления персоналом членами приемной комиссии Стэнфорда и исключить это фиктивное образование? Неужели сам факт выбрасывания больших денег и двух лет жизни демонстрирует ту приверженность бизнесу, которую работодатели находят столь привлекательной?» (Из рецензии Майкла Льюиса на книгу Питера Робинсона Snapshots from Hell: The Making of an MBA («С “Поляроидом” в аду: как получают MBA»), опубликованной в разделе «Книжное обозрение» газеты New York Times 8 мая 1994 года.) Какой ответ на вопрос Льюиса вы можете дать с учетом анализа стратегий в ситуациях с асимметрией информации?
U13 (дополнительное упражнение; необходимо ознакомиться с приложением). Налоговый инспектор анализирует последнюю налоговую декларацию Ванды (см. ), в которой она сообщает, что у нее выдался плохой год. Предположим, Ванда применяет равновесную стратегию и налоговый инспектор это знает.
a) С помощью правила Байеса найдите вероятность того, что у Ванды был хороший год, при условии, что в налоговой декларации указано обратное.
b) Объясните, почему вероятность, полученная в пункте а, больше или меньше исходной вероятности хорошего года, составляющей 0,6.
U14 (дополнительное упражнение; необходимо ознакомиться с приложением). Вернитесь к . Предположим (вполне обоснованно), что вероятность поломки «лимона» повышается с увеличением пройденного пути. В частности, пусть q = m / (m + 500), где m — длина пути в милях.
a) Найдите минимальное целое количество миль m, позволяющее предотвратить крах рынка «апельсинов». Другими словами, при каком минимальном значении m продавец «апельсина» готов его продать по рыночной цене на автомобили марки Citrus, успешно совершившие поездку? (Подсказка: не забудьте вычислить fуточ. и pуточ..
b) Какое минимальное целое количество миль m позволит добиться полного разделения действующих рынков сбыта «апельсинов» и «лимонов»? То есть при каком минимальном значении m владелец «лимона» так и не решится совершить такую поездку?

