8 Неопределенность и информация
В мы уже упоминали о различных способах возникновения в игре неопределенности (внешняя и стратегическая) и о том, что игроки могут располагать ограниченной информацией (несовершенной и неполной, симметричной и асимметричной) о разных аспектах игры: с некоторыми из них мы уже сталкивались и анализировали. В частности, в играх с одновременными ходами присутствует стратегическая неопределенность, поскольку каждый игрок не знает, какие действия предпринимает другой игрок. В мы говорили о том, что стратегическая неопределенность порождает асимметричную и несовершенную информацию, потому что различные действия, предпринимаемые одним игроком, необходимо объединить в одно информационное множество другого игрока. В и мы рассказывали, как решить проблему стратегической неопределенности посредством формирования у каждого игрока определенных убеждений в отношении действий другого игрока (в том числе убеждений о вероятности выполнения различных действий в случае использования смешанной стратегии) и применения концепции равновесия Нэша, в котором эти убеждения находят подтверждение. В данной главе мы сфокусируемся на других способах возникновения неопределенности и информационных ограничений в играх.
Начнем с анализа различных стратегий, позволяющих отдельным людям и обществам в целом справляться с несовершенством информации, возникающим в результате внешней неопределенности или риска. Напомним, что внешняя неопределенность обусловлена причинами, неподконтрольными игрокам, но при этом влияющими на их выигрыши; погода — один из простых примеров. Мы представим вам ряд базовых идей, лежащих в основе диверсификации или распределения риска отдельным игроком или объединения рисков несколькими игроками. Эти стратегии способны принести пользу всем игрокам, хотя распределение общего выигрыша между участниками может быть неравномерным, из-за чего в ситуациях такого рода наблюдается смешение общих интересов и конфликта.
Далее рассмотрим информационные ограничения в ситуациях со стратегической взаимозависимостью. Информация в игре считается полной только тогда, когда все правила игры (стратегии игроков и выигрыши каждого из них как функции стратегий всех игроков) полностью известны всем игрокам и, более того, являются их общим знанием. При столь строгом стандарте в большинстве игр присутствует неполная информация. Кроме того, зачастую неполнота информации асимметрична: каждый игрок знает собственные возможности и выигрыши гораздо лучше, чем возможности других игроков. Как отмечалось в , манипулирование информацией — важный аспект стратегий в таких играх. В этой главе мы обсудим, когда информацию можно или нельзя передать в устной форме достоверным способом. Кроме того, проанализируем другие стратегии, предназначенные для передачи или сокрытия игроком своей информации, а также ее получения от другого игрока. В и вкратце анализировались некоторые из таких стратегий (скрининг и сигнализация), сейчас же мы остановимся на них более подробно.
Безусловно, участники многих игр хотели бы иметь возможность манипулировать действиями других игроков. Руководители хотели бы, чтобы подчиненные усердно трудились и качественно выполняли свою работу; страховые компании хотели бы, чтобы держатели страховых полисов проявляли осторожность, чтобы снизить страховой риск. Если бы информация была совершенной, действия игроков поддавались бы наблюдению. Оплату труда сотрудников можно было бы поставить в зависимость от качества и количества их усилий; страховое возмещение держателям страховых полисов можно было бы выплачивать только в случае, если они предпринимают необходимые меры предосторожности. Но в действительности все эти действия трудно отслеживать, что создает ситуацию с несовершенной асимметричной информацией, обычно обозначаемую термином моральный риск. В связи с этим участники таких игр вынуждены изобретать различные непрямые способы создания стимулов, позволяющих влиять на действия других игроков в нужном направлении.
Исследования по теме информации и манипулирования ею в играх очень активизировались в последние десятилетия и пролили свет на многие ранее не совсем понятные аспекты экономики, в частности природу стимулирующих контрактов, организационную структуру компаний, рынки труда и товаров длительного пользования, государственное регулирование бизнеса и множество других аспектов. Не так давно политологи применили эти же концепции для объяснения зависимости изменений в налоговой и бюджетной политике от выборов, а также делегирования законодательных полномочий комитетам. Эти идеи распространились и в биологии, где эволюционная теория игр рассматривает такие отличительные характеристики, как большой невероятно красивый хвост павлина в качестве сигнала. Пожалуй, еще более важно, чтобы вы поняли, насколько значимы скрининг и сигнализирование в вашем повседневном взаимодействии с членами семьи, друзьями, учителями, коллегами и прочими людьми, что позволит вам совершенствовать свои стратегии в подобных играх.
Хотя изучение информации явно выходит за рамки анализа внешней неопределенности и базовых концепций сигнализирования и скрининга, тем не менее мы сфокусируемся в данной главе только на этих темах. К анализу информации и манипулирования ею мы вернемся в , где используем описанные в данной главе методы для разработки механизмов создания стимулов и получения конфиденциальной информации от других игроков.
1. Несовершенная информация: преодоление риска
Представьте, что вы фермер и ваша работа зависит от прихотей погоды. Если погода способствует хорошему урожаю, вы получите доход 160 000 долларов. Если сложатся неблагоприятные метеорологические условия, ваш доход составит всего 40 000 долларов. Эти две возможности в равной степени вероятны (вероятность каждой из них: 1/2, или 0,5, или 50%). Следовательно, ваш средний, или ожидаемый, доход равен 100 000 долларов 100 000 = 1/2 × 160 000 + 1/2 × 40 000, однако это среднее значение сопряжено со значительным риском.
Что вы можете сделать, чтобы уменьшить имеющийся риск? Попробовать выращивать культуру, которая менее подвержена капризам погоды. Но предположим, что вы уже сделали все от вас зависящее. В таком случае вы могли бы попытаться снизить риск еще больше, предложив кому-то принять на себя его часть. Безусловно, в обмен вам придется что-то этому человеку дать. Такой равноценный обмен обычно принимает две формы: денежный платеж или взаимный обмен либо разделение риска.
А. Разделение риска
Сначала проанализируем возможность взаимовыгодного разделения риска. Предположим, ваш приятель сталкивается с аналогичным риском, но в то время, когда у вас плохая погода, на его ферме погода хорошая и наоборот. (Допустим, вы живете на противоположных концах острова и дождевые облака приходят либо на одну, либо на другую его сторону, но не на обе сразу.) Корреляция — это зависимость между двумя любыми неопределенными величинами (в данном примере между риском одного фермера и риском другого). Следовательно, можно сказать, что между риском вашего приятеля и вашим риском существует полная отрицательная корреляция. Ваш с приятелем совокупный доход составляет 200 000 долларов, какой бы ни была погода, то есть он совершенно безрисковый. Вы можете заключить между собой контракт, по условиям которого каждый из вас получит гарантированных 100 000 долларов: вы обещаете выплачивать приятелю 60 000 долларов в те годы, когда вам сопутствует удача, а он — в те годы, когда ему сопутствует удача. Объединив свои риски, вы их устраняете.
Валютные свопы — еще один показательный пример отрицательной корреляции рисков в реальной жизни. Американская компания, экспортирующая продукцию в Европу, получает доход в евро, но ее интересует прибыль в долларах, зависящая от колебаний обменного курса евро–доллар. Со своей стороны, европейская компания, экспортирующая продукцию в США, сталкивается с аналогичной неопределенностью в отношении прибыли, выраженной в евро. Когда курс евро по отношению к доллару падает, доход американской компании в евро составляет меньшую сумму в долларах, а долларовый доход европейской компании — более крупную сумму в евро. Когда курс евро по отношению к доллару повышается, складывается противоположная ситуация. Таким образом, колебания обменного курса создают отрицательно коррелированные риски для обеих компаний. Следовательно, обе могут их снизить, заключив контракт о соответствующем обмене доходами.
Даже при отсутствии отрицательной корреляции разделение рисков имеет свои преимущества. Вернемся к вашей роли фермера и допустим, что вы с приятелем сталкиваетесь с рисками, не зависящими друг от друга, как если бы тучи подбрасывали монету, чтобы решить, на какую сторону острова отправиться. В таком случае существуют четыре возможных исхода, каждый с вероятностью 1/4. Ваш с приятелем доход при этих четырех исходах представлен в левой части рис. 8.1. Но предположим, вы должны заключить контракт о разделении риска поровну; тогда ваш доход будет отображен в правой части рис. 8.1. Ваш средний (ожидаемый) доход в каждой таблице составляет 100 000 долларов, однако без договора о разделении риска каждый из вас получил бы 160 000 долларов, или 40 000 долларов с вероятностью 1/2 каждый. При наличии контракта вы оба получили бы по 160 000 долларов с вероятностью 1/4, по 100 000 долларов с вероятностью 1/2 и 40 000 долларов с вероятностью 1/4. Таким образом, контракт о разделении риска позволяет каждому из вас снизить вероятность двух крайних исходов с 1/2 до 1/4 и повысить вероятность среднего исхода с 0 до 1/2. Иными словами, контракт уменьшил риск каждого из вас.
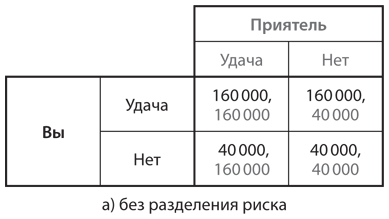
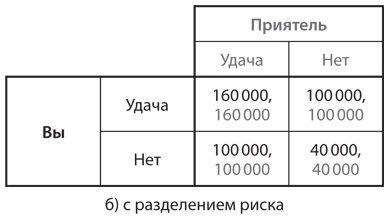
Рис. 8.1. Разделение риска в связи с получением дохода
В действительности вы с приятелем можете уменьшать свои риски посредством их разделения при условии, что между вашими доходами нет полной положительной корреляции (то есть до тех пор, пока удача не улыбнется вам обоим). А группе более двух человек, риски которых в определенной мере независимы друг от друга, закон больших чисел позволяет еще сильнее снизить риск каждого участника. Именно так и поступают страховые компании: объединив подобные, но независимые риски многих людей, они могут выплатить страховое возмещение каждому, кто понесет существенные убытки. Этот же принцип лежит в основе диверсификации инвестиционного портфеля: вкладывая средства во много разных активов с разными типами и степенями риска, вы тем самым уменьшаете общий уровень подверженности риску.
Однако такие механизмы разделения рисков зависят от публичной наблюдаемости результатов и возможности контролировать выполнение условий контракта. В противном случае у каждого фермера возникает соблазн сделать вид, что ему не повезло, или просто нарушить условия договора о разделении риска, когда ему сопутствует удача. Точно так же страховая компания может безо всяких оснований отказать в выплате страхового возмещения, но желание сохранить репутацию может удержать ее от этого шага.
Теперь рассмотрим еще один вопрос. В обсуждении выше мы исходили из того, что разделение риска осуществляется в равных долях. Это кажется естественным, поскольку вы и ваш приятель-фермер находитесь в одинаковых ситуациях. Но у вас могут быть разные стратегические навыки и возможности, и один из вас умеет лучше вести переговоры и, соответственно, добиваться большего при заключении контрактов.
Для того чтобы это понять, мы должны признать, что фермеры стремятся заключать договоренности о разделении рисков по причине их нерасположенности к риску. Как объясняется в , отношение к риску можно определить путем использования нелинейной шкалы для перевода денежного дохода в показатели полезности. Функция квадратного корня — простой пример такой шкалы, отображающей нерасположенность к риску, и мы применим ее здесь.
Когда вы несете полный риск получения 160 000 долларов или 40 000 долларов с вероятностью 1/2 в каждом случае, ваша ожидаемая полезность (взвешенное по вероятности среднее) составляет
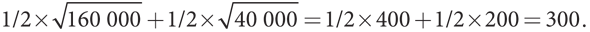
Безрисковый доход, обеспечивающий вам такую же полезность, — это число, квадратный корень которого равен 300, то есть 90 000 долларов, что меньше вашего среднего денежного дохода в размере 100 000 долларов. Разность в 10 000 долларов — максимальная сумма денег, которую вы будете готовы заплатить в качестве цены за полное устранение риска, которому подвержен ваш доход. Ваш приятель подвержен аналогичному риску, поэтому при использовании той же шкалы полезности он также будет готов заплатить эту же максимальную сумму за его полное устранение.
Рассмотрим ситуацию, когда между вашими рисками существует совершенная отрицательная корреляция и сумма вашего совокупного дохода составляет 200 000 долларов независимо от обстоятельств. Вы делаете приятелю следующее предложение: я заплачу тебе 90 001 – 40 000 = 50 001 доллар в случае неудачного года, а ты мне 160 000 – 90 001 = 69 999 долларов, когда у тебя будет урожайный год. В результате ваш приятель получит доход в размере 90 001 доллар как в неудачном, так и удачном году (160 000 – 69 999 долларов в первом случае и 40 000 + 50 001 доллар во втором). Он предпочтет эту ситуацию перспективе столкнуться с риском. Когда ему сопутствует удача, а вам — нет, у вас есть 40 000 долларов собственного дохода и вы получаете еще 69 999 долларов от приятеля, то есть ваш доход в сумме равен 109 999 долларов. Когда вашего приятеля постигает неудача, а у вас все будет хорошо, у вас есть 160 000 собственного дохода и после выплаты приятелю 50 001 доллара остается 109 999 долларов. Кроме того, вы устраняете свой риск. В итоге вы с приятелем оба выигрываете от сделки, но вы оставили за собой почти весь выигрыш.
Безусловно, приятель мог бы сделать вам встречное предложение. Кроме того, еще существует целый диапазон промежуточных предложений, подразумевающих более справедливое распределение выигрышей от разделения рисков. Какое из них одержит верх? Как мы увидим в , весь диапазон взаимовыгодных исходов разделения риска согласуется с границей эффективности переговоров в переговорной игре между игроками.
Б. Плата за снижение риска
Теперь рассмотрим возможность продажи рисков за деньги. Предположим, вы фермер, столкнувшийся с тем же риском, что и в предыдущем примере, но теперь ваш приятель имеет гарантированный доход в размере 100 000 долларов. Ваш риск увеличился, а приятель вообще не несет никакого риска. Возможно, он согласится принять на себя часть вашего риска по цене, приемлемой для вас обоих. Мы только что видели, что 10 000 долларов — максимальный «страховой взнос», который вы готовы выплатить за полное устранение риска. Примет ли ваш приятель эту сумму в качестве платы за устранение вашего риска? По сути, он берет на себя свой безрисковый доход в размере 100 000 долларов плюс ваш рисковый доход, то есть 100 000 + 160 000 = 260 000 долларов, если вам будет сопутствовать удача, и 100 000 + 40 000 = 140 000 долларов, если вам не повезет. Приятель выплатит вам 90 000 долларов в любом из этих случаев; при этом у него останется либо 170 000 долларов, либо 50 000 долларов с равной вероятностью. Следовательно, ожидаемая полезность вашего приятеля равна
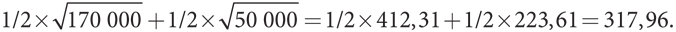
Если приятель не заключит с вами сделку, его ожидаемая полезность составит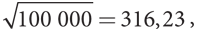 а значит, сделка принесет ему немного больше выгоды. Диапазон взаимовыгодных сделок в данном случае очень узкий, поэтому исход почти предопределен, но если вы намерены продать весь свой риск, остается совсем малый диапазон возможных взаимовыгодных вариантов.
а значит, сделка принесет ему немного больше выгоды. Диапазон взаимовыгодных сделок в данном случае очень узкий, поэтому исход почти предопределен, но если вы намерены продать весь свой риск, остается совсем малый диапазон возможных взаимовыгодных вариантов.
А как насчет частичной торговли риском? Предположим, вы заплатите приятелю сумму x, если вам будет сопутствовать удача, а он вам сумму y, если вам не повезет. Для того чтобы это привело к повышению ожидаемой полезности в случае каждого из вас, необходимо выполнить следующих два неравенства:
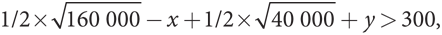
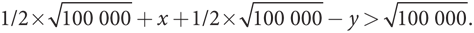
В качестве примера допустим, что y = 10 000. Тогда второе неравенство дает x > 10 526,67, а первое — x < 18 328,16. Первое значение x — минимальная плата, которую приятель потребует за готовность взять на себя ваш риск, а второе значение x — максимальная сумма, которую вы готовы заплатить ему за это. Таким образом, имеем довольно большой диапазон возможностей для взаимовыгодного обмена и торга.
А что если ваш приятель нейтрален к риску, то есть его интересуют только ожидаемые денежные показатели? Тогда, чтобы сделка стала для него приемлемой, она должна удовлетворять условию:
1/2 × (100 000 + x) + 1/2 × (100 000 − y) > 100 000,
или просто x > y. В такой ситуации возможно почти полное страхование от риска, при котором вы платите приятелю 60 001 доллар, если вам сопутствует удача, а он вам 59 999 долларов, если вам не повезет. Это и есть ситуация, в которой вы получаете весь выигрыш от торговли рисками.
Если на самом деле в роли вашего «приятеля» выступает страховая компания, она может быть почти нейтральной к риску, поскольку объединяет множество аналогичных рисков и принадлежит хорошо диверсифицированным инвесторам, для каждого из которых этот бизнес составляет всего лишь часть их общего риска. В таком случае вымышленный образ дружелюбного, нейтрального к риску, доброго фермера может стать реальностью. А если страховые компании конкурируют за страхование вашего бизнеса, страховой рынок может предложить вам почти полное страхование по цене, позволяющей вам оставить себе почти весь выигрыш.
Общей для всех этих договоренностей является идея, что заключение взаимовыгодных сделок возможно при условии, что тот, кто сталкивается с меньшим риском, снимает его часть с того, кто подвержен большему риску. На самом деле идея о существовании цены за риск и рынка риска лежит в основе почти всех финансовых механизмов в современной экономике. Акции и облигации, а также все сложные финансовые инструменты, такие как деривативы, — лишь способ распределения риска среди тех, кто готов его нести за минимальную цену. Многие считают, что такой рынок — в чистом виде азартная игра, и в каком-то смысле это так и есть. Однако те, кто стартует с минимального риска, соглашаются участвовать в подобных играх, возможно, потому, что уже обеспечили себе диверсификацию способом, о котором шла речь выше. А те, кто изначально наиболее подвержен риску, продают или избавляются от него. Это позволяет последним рисковать больше, чем в случае, если бы им приходилось нести весь риск на себе. Следовательно, финансовые рынки стимулируют предпринимательство, содействуя торговле рисками.
Итак, мы рассмотрели только разделение заданного общего риска. В реальной жизни существует возможность предпринять действия, направленные на уменьшение общего риска: фермер может защитить посевы от мороза, а владелец автомобиля — осторожнее им управлять, чтобы снизить риск аварии. Если такие действия не поддаются публичному наблюдению, это игра с несовершенной информацией, и возникает проблема морального риска, о которой говорилось выше: у хорошо застрахованных людей нет стимула снижать риск, с которым они сталкиваются. Мы рассмотрим подобные проблемы, а также механизмы их преодоления, в .
В. Манипулирование риском в соперничестве
Фермеры, о которых шла речь выше, столкнулись с риском из-за погодных условий, а не собственных действий или действий других фермеров. Если участники игры могут оказывать влияние на риск, которому подвержены они сами или другие игроки, то они могут использовать такое манипулирование риском стратегически. Наглядный пример — соперничество в области исследований и разработок между компаниями, стремящимися превзойти друг друга в разработке и выводе на рынок новых информационных технологий или биотехнологических продуктов; многим спортивным соревнованиям свойственны аналогичные характеристики.
В спорте и других типах соперничества такого рода исход игры зависит от комбинации мастерства и удачи. Вы одержите победу, если
ваше мастерство + ваша удача > мастерство соперника + удача соперника
или если
ваше удача − удача соперника > мастерство соперника – ваше мастерство.
Обозначим левую сторону последнего неравенства символом L; это ваш «избыток удачи». L — неопределенная величина; предположим, распределение ее вероятностей — это нормальная, или колоколобразная, кривая, показанная на рис. 8.2 в виде черной кривой. В любой точке на горизонтальной оси высота этой кривой представляет вероятность, с которой L принимает соответствующее значение. Следовательно, область под кривой между любыми двумя точками на горизонтальной оси равна вероятности того, что L лежит между этими двумя точками. Допустим, у вашего соперника уровень мастерства выше, а значит, вы более слабый игрок. Ваш «дефицит мастерства», эквивалентный разности между навыками соперника и вашими, имеет положительное значение, как показано в точке S. Вы одержите победу, если ваш избыток удачи L превосходит ваш дефицит мастерства S. Стало быть, область под кривой справа от точки S, заштрихованная на рис. 8.2, представляет вероятность вашей победы. Если привнести в ситуацию больше случайности, колоколобразная кривая станет более пологой (как серая кривая на рис. 8.2), поскольку вероятность относительно высоких и низких значений L повышается, тогда как вероятность средних значений снижается. В таком случае область под кривой справа от точки S также увеличивается. На рис. 8.2 область под исходной кривой нормального распределения заштрихована перекрестными линиями, а более крупная область под пологой кривой — однонаправленными. В качестве аутсайдера вы должны придерживаться стратегии, которая сглаживает эту кривую. И напротив, если вы фаворит, вам следует попытаться сократить элемент случайности в состязании.
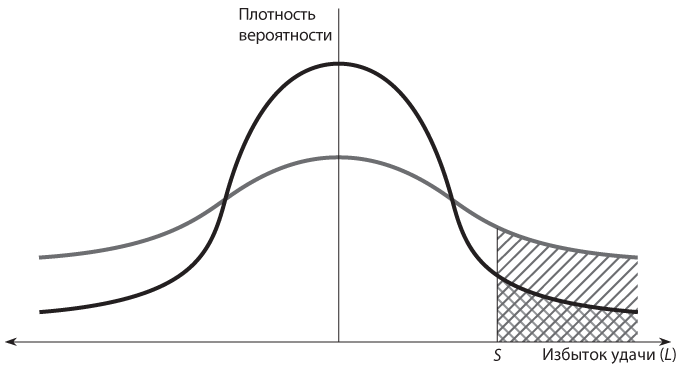
Рис. 8.2. Влияние повышения риска на вероятность победы
Таким образом, мы должны воспринимать более слабых игроков или тех, кто отстал в длинной гонке, как людей, пытающихся применить неформатные или рискованные стратегии, поскольку это их единственный шанс наверстать упущенное или вырваться вперед. Напротив, игроки, имеющие максимальные шансы на успех или преимущество в игре, будут вести осторожную игру. Вот практический совет, основанный на этом принципе: если вы хотите бросить вызов тому, кто играет в теннис лучше вас, выберите для матча ветреный день.
Вы можете извлечь для себя выгоду из манипулирования не только величиной риска в вашей стратегии, но и корреляцией между рисками. Опережающий вас игрок попытается выбрать максимально высокую положительную корреляцию; тогда независимо от того, сопутствует ли ему самому удача или нет, удача его соперника останется неизменной и его преимущество в игре будет защищено. Напротив, отстающий игрок постарается найти риск, как можно меньше коррелирующий с риском соперника. Общеизвестно, что в гонке между двумя парусниками яхта, находящаяся позади, должна следовать по другому пути, чем яхта, которая вырвалась вперед и должна повторять все маневры отстающей.
2. Асимметричная информация: основные идеи
Во многих играх один или несколько игроков могут иметь преимущество за счет того, что они с большей определенностью знают, что произошло или произойдет. Такие преимущества, или асимметричность информации, присущи реальным стратегическим ситуациях. На самом базовом уровне каждый игрок может знать собственные предпочтения или выигрыши, скажем, терпимость к риску в игре «балансирование на грани», терпение в переговорах, а также мирные или воинственные намерения в международных отношениях. Однако при этом у него могут быть весьма расплывчатые представления о предпочтениях или выигрышах других игроков. То же касается и знания игроком своих характеристик (таких как уровень квалификации работника или склонность к риску у человека, подающего заявку на страхование автомобиля или медицинское страхование). Иногда действия, доступные одному игроку (например, вооружение и боеготовность страны), не в полной мере известны другим игрокам. И наконец, некоторые фактические результаты (фактический объем убытков, понесенных застрахованным домовладельцем в результате наводнения или землетрясения) может видеть один игрок, но не другие.
Манипулирование информацией о ваших способностях и предпочтениях, известной другим игрокам, позволяет влиять на равновесный исход игры. В результате такое манипулирование асимметричной информацией само по себе становится стратегической игрой. Возможно, вы считаете, что каждый игрок всегда стремится скрывать свою информацию и получать информацию от других игроков, но это не так. Ниже представлен список различных возможностей вместе с примерами. Более информированный игрок может предпринять следующие действия:
- Скрыть или дать ложную информацию. При смешивании ходов в игре с нулевой суммой вы не хотите, чтобы другой игрок видел, что вы делаете. Так вы блефуете в покере, чтобы ввести в заблуждение других игроков относительно ваших карт.
- Раскрыть часть правдивой информации. Когда вы предпринимаете стратегический ход, вам нужно, чтобы другие игроки видели, что именно вы сделали, и отреагировали соответствующим образом. Например, если вы оказались в напряженной ситуации, но у вас нет враждебных намерений, вам необходимо убедить других в их достоверности, чтобы не завязалась ненужная схватка.
В свою очередь менее информированный игрок может предпринять одно из следующих действий:
- Получить необходимую информацию или отделить правду от лжи. Например, работодатель хочет определить уровень квалификации потенциального сотрудника или объем усилий, вкладываемых в работу наемным работником. Страховой компании необходимо знать категорию риска человека, подающего заявление о страховании, и объем убытков человека, подающего заявление о выплате страхового возмещения, а также информацию о любой небрежности страхователя, предполагающей возмещение доли его ответственности.
- Оставаться в неведении. Незнание о стратегическом ходе соперника может оградить вас от его обязательств и угроз. Политики или руководители высшего уровня часто извлекают выгоду из такого «достоверного отрицания».
Обычно одних только слов для передачи достоверной информации бывает недостаточно: судят скорее по делам, чем по словам. Но даже действия не всегда эффективны, если любой игрок может без труда их выполнить. Тем не менее в целом менее информированным игрокам следует обращать внимание на действия более информированного игрока, а не на то, что он говорит. А более информированный игрок, в свою очередь, зная о том, что другие игроки будут интерпретировать его действия таким образом, должен попытаться манипулировать их информационным содержанием.
В ходе стратегической игры вы можете обнаружить, что владеете информацией, которой нет у других игроков. В вашем распоряжении может оказаться информация, «хорошая» именно для вас в том смысле, что, узнай о ней другие игроки, они изменили бы свои действия так, что это увеличило бы ваш выигрыш. Например, вам точно известно, что вы некурящий, поэтому вы должны претендовать на более низкие взносы по страхованию жизни. С другой стороны, у вас может быть «плохая» информация, раскрытие которой обусловило бы действия других игроков, способные вам навредить. Например, в колледже вы получали оценки обманным путем и не заслуживаете принятия на учебу в престижную юридическую школу. Вы знаете, что окружающие составят о вас мнение на основании ваших действий, и в связи с этим попытаетесь придумать и предпринять шаги, которые заставят их решить, что ваша информация заслуживает доверия. Такие действия называются сигналами, а стратегия их использования — сигнализированием. И наоборот, если окружающие посчитают, что ваша информация не заслуживает доверия, вы можете помешать им в этом утвердиться, попытавшись ввести их в заблуждение. Такие стратегии, обозначаемые термином «подавление сигнала», как правило, относятся к числу смешанных, поскольку случайный характер смешанных стратегий не позволяет делать точные логические выводы.
Если другие игроки знают больше вас или совершают действия, которые нельзя непосредственно наблюдать, вы можете использовать стратегии, которые сократят такое информационное отставание. Стратегия, вынуждающая другого игрока раскрыть свою информацию, называется скринингом, а конкретные методы, используемые с этой целью, — инструментами скрининга.
Поскольку личная информация игрока часто включает в себя знания о его способностях или предпочтениях, полезно думать об игроках, вступающих в игру с разной личной информацией, как об игроках различных типов. При наличии достоверного сигнализирования в равновесии игры менее информированные игроки смогут делать правильные выводы об информации, имеющейся у более информированных игроков, на основании их действий. Например, юридическая школа примет на учебу только абитуриентов, прошедших надлежащий отбор. Этот исход еще можно описать так: в равновесии разные типы игроков правильно раскрываются или разделяются, поэтому мы называем данную ситуацию разделяющим равновесием. Тем не менее иногда игроки одного или более типов могут успешно имитировать действия игроков других типов с тем, чтобы неинформированные игроки не могли определять различные типы игроков и идентифицировать их действия; например, страховые компании могут предлагать только одну разновидность страховых полисов. В таком случае мы говорим, что в равновесии типы объединяются, и называем его объединяющим равновесием. В процессе изучения игр с неполной информацией мы увидим, что идентификация типа равновесия, присутствующего в игре, имеет первостепенное значение.
3. Непосредственная коммуникация, или дешевый разговор
Обычно самый простой способ передать информацию другим — просто сообщить им ее. Точно так же самый простой способ получить информацию — попросить предоставить ее. Однако участники стратегической игры должны осознавать, что другие игроки не всегда говорят правду сами и не всегда поверят чьим-то утверждениям. То есть достоверность сказанных слов может быть поставлена под сомнение. Есть такое распространенное изречение: «слова стоят дешево»; непосредственная коммуникация действительно не требует прямых затрат, или они настолько незначительны, что их можно не принимать в расчет. Тем не менее она может косвенно повлиять на исходы игры и выигрыши игроков путем изменения убеждений одного игрока в отношении действий другого игрока или воздействия на выбор одного равновесия из множества равновесий. Непосредственную коммуникацию, не требующую прямых затрат, специалисты по теории игр называют «дешевым разговором», а равновесие, достигнутое в результате ее использования, обозначается термином «равновесие дешевого разговора».
А. Полностью совпадающие интересы
Прямая передача информации оправдывает себя в случаях, когда интересы игроков полностью совпадают. Игра в доверие, описанная в , — самый яркий пример данной ситуации. Таблица этой игры (см. ) воспроизведена на рис. 8.3.
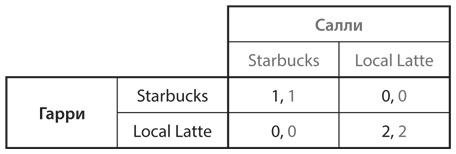
Рис. 8.3. Игра в доверие
В этой игре интересы Гарри и Салли полностью совпадают: оба хотят встретиться и оба предпочитают сделать это в Local Latte. Проблема в том, что эта игра носит некооперативный характер: ее участники делают выбор независимо друг от друга, не зная о выборе другого игрока. Но давайте представим, что у Гарри появляется возможность отправить Салли сообщение (или Салли получает возможность задать вопрос, на который Гарри отвечает), прежде чем оба сделают выбор. Если сообщение Гарри «Я иду в Local Latte», у Салли нет оснований думать, что он лжет. И если Гарри считает, что Салли поверит ему, для него в равной мере оптимально выбрать Local Latte, сделав свое сообщение правдивым. Таким образом, непосредственная коммуникация позволяет быстро добиться предпочтительного для обоих игроков исхода. Именно этим объясняется тот факт, что при анализе данной игры в нам пришлось придумать сложный сценарий, при котором коммуникация была невозможна: вспомните, что Гарри и Салли до последней минуты перед встречей были на разных занятиях и у них не было мобильных телефонов.
Давайте более детально проанализируем исход игры в доверие при наличии непосредственного общения с точки зрения теории игр. Предположим, мы сконструировали двухэтапную игру. На первом этапе действует только Гарри, и это передача сообщения Салли. На втором этапе разыгрывается исходная игра с одновременными ходами. В полной двухэтапной игре происходит равновесие обратных рассуждений, в котором стратегии (исчерпывающие планы действий) заключаются в следующем. План действий обоих игроков на втором этапе таков: «Если сообщение Гарри на первом этапе “Я иду в Starbucks”, то выбрать Starbucks; если сообщение Гарри на первом этапе “Я иду в Local Latte”, выбрать Local Latte». (Помните, что в играх с последовательными ходами игроки должны использовать исчерпывающие планы действий.) Действие Гарри на первом этапе сводится к отправке сообщения: «Я иду в Local Latte». Подтвердить, что это и есть равновесие обратных рассуждений в данной двухэтапной игре, не составит труда, поэтому мы оставляем эту задачу вам.
Однако равновесие, в котором применим дешевый разговор, не единственное равновесие обратных рассуждений в данной игре. Рассмотрим следующие стратегии: план действий каждого игрока на втором этапе — пойти в Starbucks независимо от сообщения, отправленного Гарри на первом этапе, то есть оно может быть любым. Можно убедиться, что эта совокупность стратегий также представляет собой равновесие обратных рассуждений. Независимо от сообщения Гарри на первом этапе, если один игрок отправится в Starbucks, то для другого игрока будет оптимальным пойти туда же. Таким образом, в каждой из подыигр, которые могут возникнуть на втором этапе (по одной подыгре после каждого из двух сообщений Гарри), выбор Starbucks обоими игроками и есть равновесие Нэша в соответствующей подыгре. В таком случае на первом этапе Гарри будет безразлично, какое сообщение отправить, поскольку он знает, что оно будет проигнорировано.
Равновесие дешевого разговора (при котором сообщение Гарри не игнорируется) обеспечивает более высокие выигрыши, и мы могли бы предположить, что именно оно будет выбрано в качестве фокальной точки. Тем не менее наличие причин исторического или культурного характера может обусловить выбор другого равновесия. Например, по неким причинам, не имеющим никакого отношения к данной игре, у Гарри может быть репутация абсолютно ненадежного человека. Он может быть неисправимым шутником или просто невнимательным человеком. В таком случае люди могут не доверять его заявлениям, и Салли, зная, что это обычное положение вещей, не поверит сообщению Гарри.
Подобные проблемы присущи всем коммуникационным играм. В них всегда есть альтернативные равновесия, в которых коммуникация не принимается во внимание, а значит, не играет особой роли. Специалисты по теории игр называют их равновесиями пустого разговора. Однако мы ограничимся лишь упоминанием о них и сосредоточимся на равновесиях дешевого разговора, в которых коммуникация действительно влечет за собой определенные последствия.
Б. Полностью противоположные интересы
Достоверность непосредственной коммуникации зависит от степени согласованности интересов игроков. В качестве разительного контраста с игрой в доверие рассмотрим игру, в которой интересы игроков диаметрально противоположны, а именно игру с нулевой суммой. Яркий пример такой игры — розыгрыш очка в теннисе на ; мы воспроизводим ее таблицу выигрышей на рис. 8.4. Помните, что в качестве выигрышей выступает процент успешных ударов Эверт. Не забывайте также, что в этой игре есть только равновесие Нэша в смешанных стратегиях (полученное в ); ожидаемый выигрыш Эверт в нем равен 62.
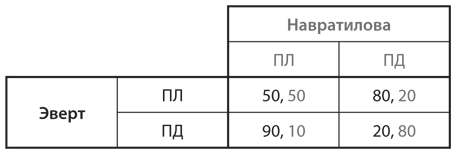
Рис. 8.4. Игра в розыгрыш очка в теннисе
Теперь представим, что мы построили двухэтапную игру. На первом этапе Эверт предоставляется возможность отправить сообщение Навратиловой. На втором этапе разыгрывается игра с одновременными ходами (рис. 8.4). Каким будет равновесие обратных рассуждений?
Вполне очевидно, что Навратилова не поверит ни одному сообщению, полученному от Эверт. Например, если сообщение Эверт — «Я намерена сыграть ПЛ» и Навратилова ей поверит, то Навратиловой следует выбрать стратегию «прикрывать ПЛ». Однако если Эверт придет к выводу, что Навратилова будет прикрывать ПЛ, то ей лучше применить стратегию ПД. На следующем уровне рассуждений Навратилова должна предвидеть это и не поверить в заявление Эверт о выборе ПЛ.
Но здесь есть еще кое-что. Навратилова также не должна полагать, что Эверт поступит наоборот. Предположим, сообщение Эверт: «Я намерена сыграть ПЛ», и Навратилова думает: «Она просто пытается меня обмануть, поэтому я буду исходить из того, что она выберет ПД». В результате Навратилова выбирает «прикрывать ПД». Однако если Эверт считает, что Навратилова усомнится в ее сообщении, она все же применит стратегию ПЛ. Навратилова должна предусмотреть и такой вариант развития событий.
Стало быть, недоверие Навратиловой должно означать абсолютное игнорирование сообщения Эверт. В таком случае в этой двухэтапной игре будет только равновесие пустого разговора. Действия двух ее участниц на втором этапе будут представлять собой равновесие в исходной игре, а сообщение Эверт на первом этапе может быть любым. Это характерно для всех игр с нулевой суммой.
В. Частично совпадающие интересы
А как насчет общих игр, где есть смешение конфликта и общих интересов? Заслуживает ли в них доверия непосредственная коммуникация, зависит от того, как смешиваются конфликт и сотрудничество при частичном совпадении интересов игроков. Таким образом, в подобных играх следует ожидать наличия как равновесия дешевого разговора, так и равновесия пустого разговора. В общем случае, чем больше совпадают интересы, тем больше информации должно быть доступно для передачи. Мы проиллюстрируем этот интуитивный вывод на следующем примере.
Рассмотрим ситуацию, с которой вы уже, возможно, сталкивались, а если нет, то это обязательно произойдет, как только вы начнете зарабатывать и инвестировать деньги. Когда финансовый консультант советует вам сделать инвестицию, он может предложить вам формирование долгосрочных отношений для получения стабильных комиссионных либо он может оказаться мошенником, который навяжет вам свой вариант инвестиций, заберет авансовые комиссионные и исчезнет. Достоверность его рекомендаций зависит от того, отношения какого типа вы с ним установите.
Предположим, вы намерены инвестировать 100 000 долларов в актив, рекомендованный консультантом, и предвидите три возможных исхода. Актив может оказаться плохим объектом для инвестиций (П), что приведет к убыткам в размере 50%, то есть получению выигрыша −50, выраженного в тысячах долларов. Актив может оказаться средним объектом для инвестиций (С) и обеспечит рентабельность инвестиций в размере 1%, или выигрыш 1. И наконец, он может стать хорошим объектом для инвестиций (Х), обеспечивающим рентабельность 55%, или выигрыш 55. Решив инвестировать, вы авансом платите консультанту комиссионные в размере 2% независимо от эффективности инвестиций, что дает ему выигрыш 2 и одновременно снижает ваш выигрыш на 2. Кроме того, консультант заработает 20% от прибыли, которую вы получите, и у вас останется выигрыш в размере 80% от прибыли, но при этом консультант не разделит с вами убытков.
Без специальных знаний о рекомендуемом активе вы не можете оценить вероятность какого-то из этих трех исходов. Поэтому вы просто полагаете, что все три варианта (П, С и Х) в равной степени возможны: каждый может наступить с вероятностью 1/3. В такой ситуации при отсутствии дополнительной информации вы рассчитываете свой ожидаемый выигрыш от инвестирования в рекомендуемый актив следующим образом:
[(1/3 × –50) + (1/3 × 0,8 × 1) + (1/3 × 0,8 × 55)] – 2 = [1/3 × (–50 + 0,8 + 44)] – 2 = [1/3 × (– 5,2)] – 2 = –1,73 – 2 = –3,73.
Согласно этому расчету, ожидаемый убыток составит 3 730 долларов. Следовательно, вы не станете вкладываться в этот актив, а ваш консультант не получит никаких комиссионных. Аналогичные вычисления показывают, что с учетом отрицательного ожидаемого выигрыша вы бы не инвестировали и в случае, если бы были убеждены, что рекомендуемый актив однозначно относится к типам П и С или представляет собой их любую взвешенную по вероятности комбинацию.
У вашего консультанта складывается иная ситуация. Он проанализировал соответствующий инвестиционный актив и точно знает, какой из трех сценариев (П, С или Х) соответствует истине. Нам необходимо определить, что он будет делать с этой информацией, в частности поделится ли ею с вами. Ниже мы рассмотрим разные возможности, исходя из предположения, что вы будете обновлять свои убеждения в отношении типа актива на основании полученной от консультанта информации. В данном примере просто условимся, что вы верите сказанному и присваиваете вероятность 1 тому, что актив относится к типу, указанному вашим консультантом.
I.-Краткосрочные отношения. Если консультант говорит вам, что рекомендуемый актив относится к типу П, вы решаете не инвестировать. Почему? Потому что ваш ожидаемый выигрыш при этом составит −50; кроме того, данная инвестиция обойдется в 2 дополнительные единицы (комиссионные консультанту), то есть ваш окончательный выигрыш будет −52. Аналогично, если консультант вам сообщит, что актив относится к типу С, вы тоже не станете инвестировать. В этом случае ваш ожидаемый выигрыш составит 80% от прибыли в размере 1 минус 2 на выплату комиссионных, то есть в сумме −1,2. Вы согласитесь только в случае, если консультант скажет, что актив относится к типу Х. Тогда ваш ожидаемый выигрыш будет 80% от прибыли в размере 55 минус 2 на выплату комиссионных, или 42.
Что при этом сделает ваш консультант со своими знаниями? Если правда — Х, он захочет сказать вам об этом, чтобы убедить инвестировать в данный актив. Но если консультант не видит перспективы ваших долгосрочных отношений, он может заявить вам, что правда — это Х, даже если на самом деле актив относится к типу С или П и он об этом знает. Если вы решите инвестировать на основании слов консультанта, он просто положит в карман 2% комиссионных и исчезнет ввиду отсутствия необходимости поддерживать с вами контакт. Зная о существовании вероятности получить плохой совет или ложную информацию от консультанта, с которым вы сталкиваетесь всего один раз, вы должны полностью игнорировать его рекомендацию. Следовательно, в этой игре с асимметричной информацией и краткосрочными отношениями достоверная коммуникация невозможна. Единственное равновесие, присутствующее здесь, — это равновесие пустого разговора; равновесия дешевого разговора в данном случае нет.
II.-Долгосрочные отношения: полное раскрытие информации. Теперь представим, что ваш консультант работает на компанию, через которую вы делаете инвестиции уже много лет: потеря будущего бизнеса с вами может стоить ему работы. Если вы инвестируете в актив, рекомендуемый консультантом, вы сможете сравнить фактическую эффективность этих инвестиций с его прогнозом. Он может оказаться ошибочным отчасти (прогноз был С, а на самом деле П или был Х, а на самом деле С) или полностью (прогноз был Х, а на самом деле П). Если вы обнаружите такое искажение информации, ваш финансовый консультант и его компания не только потеряют вас как клиента, но и рискуют потерять других клиентов, если вы расскажете друзьям и знакомым о подобных махинациях. Если ваш консультант связывает потерю репутации с определенными издержками, ваши возможные убытки косвенным образом касаются и его, а значит, его интересы частично совпадают с вашими. Предположим, незначительное искажение информации обойдется консультанту в 2 единицы выигрыша (денежный эквивалент — 2000 долларов убытка), а серьезное искажение — в 4 единицы (убыток в размере 4000 долларов). Теперь можем определить, достаточно ли частичного совпадения ваших с консультантом интересов для того, чтобы заставить его говорить правду.
Как отмечалось выше, консультант скажет вам правду, чтобы побудить вас инвестировать в определенный актив, если последний относится к типу Х. Нам необходимо проанализировать мотивы консультанта, когда актив относится не к типу Х, а к типу П или С. Сперва допустим, что актив относится к типу П. Если ваш консультант раскроет правду о типе актива, вы не станете инвестировать и он лишится комиссионных, но при этом не понесет никаких репутационных издержек: его выигрыш от описания актива как П в случае, если он действительно относится к типу П, равен 0. Если консультант вам сообщит, что актив относится к типу С (хотя на самом деле это П), вы все равно откажетесь инвестировать, поскольку ваш выигрыш составил бы −1,2, как мы подсчитали выше. В этом случае консультант тоже получит выигрыш 0, поэтому у него нет причин вам лгать о типе актива. Но что если консультант скажет, будто актив принадлежит к типу Х? Если вы поверите ему и вложите деньги, он получит авансовые комиссионные в размере двух процентов, но при этом понесет репутационные издержки 4 в связи с серьезной ошибкой. Если консультант скажет, что актив относится к типу Х, тогда как на самом деле это тип П, он получит отрицательный ожидаемый выигрыш. Иными словами, вашему консультанту выгоднее честно признаться, что актив относится к типу П.
Но что если на самом деле актив относится к типу С? Правдивое раскрытие информации не убедит вас в целесообразности инвестиций, и выигрыш консультанта составит 0. Если консультант скажет вам, что актив относится к типу Х и вы поверите ему, то вашим решением будет инвестировать. Консультант получит комиссионные в размере 2, 20 процентов от прибыли 1, которую обеспечит вам актив типа С, но при этом понесет репутационные издержки 2 в связи с частичным искажением информации. Следовательно, его выигрыш составит 2 + (0,2 × 1) – 2 = 0,2 > 0. Таким образом, консультант все же извлечет выгоду из ложного сообщения о типе актива Х, если на самом деле это С. Зная об этом, вы не поверите никаким утверждениям консультанта о том, что данный актив относится к типу Х.
Поскольку у вашего консультанта есть стимул солгать, когда рекомендуемый им актив относится к типу С, в такой ситуации достоверное раскрытие всей информации невозможно. Равновесие пустого разговора, при котором игнорируется любое сообщение консультанта, — по-прежнему одно из возможных. Однако является ли оно здесь единственным или частичная коммуникация все же реальна? Невозможность полного раскрытия информации обусловлена тем, что консультант может неправильно заявить, что актив принадлежит к типу Х, хотя на самом деле к С, поэтому объединим эти две возможности в одно событие и обозначим его как «не-П». Тогда консультант спрашивает себя, что именно ему следует вам сообщить, П или «не-П». Теперь можем проанализировать, решит ли консультант сказать вам правду в условиях такой частичной коммуникации.
III.-Долгосрочные отношения: частичное раскрытие информации. Чтобы определить мотивы вашего консультанта в ситуации «П или не-П», необходимо понять, какие выводы вы сделаете (то есть какую апостериорную вероятность вычислите) из сообщения «не-П», если вы ему поверите. Ваше предыдущее (первоначальное) убеждение состояло в том, что варианты П, С и Х в равной степени вероятны, то есть вероятность каждого из них составляет 1/3. Если консультант скажет «не-П», у вас останется два объекта для инвестиций — С и Х. Первоначально вы рассматривали их как равновероятные, и у вас нет оснований менять это предположение, поэтому теперь вы присваиваете каждому из них вероятность 1/2. Это ваша новая, апостериорная вероятность, зависящая от информации, предоставленной консультантом. С ее учетом ваш ожидаемый выигрыш при решении инвестировать после получения от консультанта сообщения «не-П» составит [1/2 × (0,8 × 1)] + [1/2 × (0,8 × 55)] – 2 = 0,4 + 22 – 2 = 20,4 > 0. Этого положительного ожидаемого выигрыша достаточно, чтобы побудить вас инвестировать.
Знание о том, что вы будете инвестировать в случае «не-П», позволяет определить, будет ли у вашего консультанта стимул солгать. Захочет ли он сказать «не-П», даже если правда П? Когда актив действительно принадлежит к типу П и консультант говорит правду (сообщает тип П), его выигрыш равен 0, как мы и вычислили выше. Если же вместо этого консультант сообщает «не-П» и вы верите ему, он получит 2 в качестве комиссионных и понесет репутационные издержки в связи с искажением информации. Поскольку вы исходите из того, что С и Х в равной степени вероятны в случае сообщения «не-П», ожидаемое значение репутационных издержек при этом составит 1/2 от издержек 4 вследствие серьезного искажения информации. Таким образом, ожидаемое значение репутационных издержек равно (1/2 × 2) + (1/2 × 4) = 3. Чистый выигрыш вашего консультанта от сообщения вам типа актива «не-П», тогда как на самом деле это П, составляет 2 – 3 = −1. Следовательно, предоставив вам ложную информацию, он ничего не выиграет. Сказать правду — его лучшая стратегия в данной ситуации, поэтому здесь возможно равновесие дешевого разговора с частичным раскрытием информации.
Концепцию равновесия дешевого разговора с частичным раскрытием информации можно уточнить с помощью концепции разбиения. Напомним, что вы предвидите три возможных сценария, или события, — П, С и Х. Это множество событий можно разделить, или разбить, на отдельные подмножества, и тогда ваш консультант сообщит вам о подмножестве, содержащем правду. (Разумеется, правдивость его сообщения предстоит проанализировать.) В данном случае мы имеем ситуацию с разбиением на два подмножества: одно, состоящее лишь из П, и второе, включающее пару событий {С, Х}. В равновесии с частичным раскрытием информации эти подмножества можно отличить друг от друга на основании сообщения консультанта, однако провести между С и Х более тонкое различие, которое бы привело к максимально точному разбиению на три подмножества, каждое из которых состояло бы из одного элемента, нельзя. Это было бы возможно только при наличии равновесия с полным раскрытием информации.
Мы намеренно сказали ранее о том, что равновесие дешевого разговора с достоверным частичным раскрытием информации возможно. Данная игра относится к категории игр со множеством равновесий, потому что в ней вероятно и равновесие пустого разговора. Конфигурация стратегий и убеждений, при которой вы игнорируете сообщение консультанта, а он отправляет одно и то же сообщение (или даже произвольное сообщение) независимо от того, что соответствует истине, и есть равновесие. С учетом стратегий каждого игрока, у другого игрока нет оснований менять свои действия или убеждения. В терминах разбиений такое равновесие пустого разговора можно считать равновесием с самым грубым, тривиальным разбиением с одним (под)множеством {П, С, Х}, включающим все три варианта. В общем случае всякий раз, когда в игре с дешевым разговором вы находите равновесие, не являющееся равновесием пустого разговора, там будет как минимум еще одно равновесие с более грубым разбиением исходов.
IV.-Множество равновесий. В качестве примера ситуации, в которой более грубые варианты разбиения связаны с дополнительными равновесиями, рассмотрим случай, когда репутационные издержки консультанта выше, чем предполагалось ранее. Пусть они равны 4 (вместо 2) в случае мелкого искажения истины и 8 (вместо 4) при крупном искажении. Согласно выполненному нами анализу, ваш консультант сообщит о типе Х, если актив действительно относится к типу Х, и о типе П, если актив относится к типу П. Эти результаты сохраняются. Консультант хочет, чтобы вы инвестировали в актив типа Х; кроме того, он по-прежнему получает тот же выигрыш от сообщения о типе П, если актив действительно относится к типу П, так же как и в случае сообщения о типе С в той же ситуации. При более высоких репутационных издержках у консультанта еще меньше мотивов лгать вам о том, что рекомендуемый им актив относится к типу Х, тогда как на самом деле это тип П. Таким образом, если актив имеет тип П или Х, можно рассчитывать, что консультант скажет правду.
Проблема с полным раскрытием информации в предыдущем примере возникла только из-за наличия у консультанта стимула солгать в случае, когда актив относится к типу С. Судя по вычисленным нами показателям, выигрыш консультанта от предоставления информации о типе Х, тогда как на самом деле это тип С, был выше, чем при обнародовании правдивой информации. Сохранится ли такое положение вещей и в ситуации с более высокими репутационными издержками?
Предположим, актив относится к типу С, а консультант сообщает о типе Х. Если вы поверите ему и инвестируете в этот актив, ожидаемый выигрыш консультанта составит 2 (комиссионные) + 0,2 × 1 (его доля в фактической прибыли на инвестиции в актив типа С) – 4 (его репутационные издержки) = −1,8 < 0. Правда принесет консультанту выигрыш 0. У него больше нет мотивов завышать качество инвестиционного актива. Исход, при котором консультант всегда говорит правду, а вы верите ему и предпринимаете соответствующее действие, и есть равновесие дешевого разговора с полным раскрытием информации. В нем возможно самое мелкое разбиение на подмножества, состоящие из одного элемента, — {П}, {С} и {Х}.
В данном случае существуют еще три равновесия, каждое с более грубым разбиением, чем при равновесии с полным раскрытием информации. Обе ситуации с двумя подмножествами (одна с подмножествами {П, С} и {Х}, а другая — {П} и {С, Х}), а также ситуация с пустым разговором с одним подмножеством {П, С, Х}, — это альтернативные равновесия, которые возможны в данной игре. Какое из них получит приоритет, зависит от условий, рассмотренных в во время анализа игры со множеством равновесий.
Самая большая реальная трудность, связанная с получением равновесия с достоверной передачей информации, не являющегося равновесием пустого разговора, состоит в знании игроками степени совпадения их интересов, причем это должно быть их общим знанием. В примере с инвестициями для вас крайне важно на основании предыдущего опыта взаимодействия с консультантом или из других источников (таких как контракт) знать, что в целях сохранения репутации он лично заинтересован в благоприятном исходе вашего инвестирования. Если бы вы не знали, в какой степени интересы консультанта совпадают с вашими, у вас были бы все основания подозревать, что он привирает, чтобы склонить вас к инвестициям ради комиссионных, которые он незамедлительно получит.
Что происходит в случае более информативных сообщений? Предположим, консультант может сообщить вам показатель g, представляющий собой его оценку темпов роста курса акций, и уточнить, что g может принимать диапазон непрерывных значений. В этой ситуации, если консультант получит дополнительную выгоду от покупки вами плохих акций по его рекомендации, у него есть стимул завысить значение g. В результате абсолютно точная и правдивая коммуникация больше невозможна. Однако равновесие дешевого разговора с частичным раскрытием информации все же вероятно. Непрерывный диапазон значений темпов роста курса акций можно разделить на интервалы (скажем, от 0 до 1%, от 1 до 2% и т. д) так, чтобы консультант посчитал оптимальным сказать вам правду о том, в какой из этих интервалов на самом деле попадает показатель темпов роста курса акций, а вы сочли бы нужным прислушаться к его совету и предпринять на его основании оптимальное действие. Чем выше ценит консультант свою репутацию, тем мельче будет разбиение диапазона значений g — например, это может быть половина процента вместо целого или четверть процента вместо половины. Дальнейшее объяснение этой темы можно найти в работах, в которых она рассматривается более углубленно.
Г. Формальный анализ игр с дешевым разговором
До сих пор наш анализ игр с дешевым разговором носил эвристический и вербальный характер. Такого подхода обычно достаточно для понимания и прогнозирования поведения, но в подобных играх существуют и при необходимости могут быть использованы формальные методы описания и решения игр — деревья и матрицы игры. Для того чтобы показать, как это делается, и связать игры, представленные в данной главе, с теорией, изложенной в предыдущих главах, проанализируем игру между вами и вашим финансовым консультантом в этом контексте. В рамках анализа будем исходить из предположения, что ваш консультант проводит различие между тремя возможными вариантами П, С и Х, сообщая вам информацию о рекомендуемом активе; иными словами, рассмотрим ее самое мелкое разбиение. Прочитав этот раздел, вы сможете выполнить аналогичный анализ для случая, когда в сообщении консультанта присутствует более грубое разбиение информации об активе на типы П или «не-П».
Начнем с построения дерева игры, представленного на рис. 8.5. Условный игрок «природа», о котором шла речь в , ходит первым, создавая один из трех вариантов доходности ваших инвестиций, а именно П, С и Х, с вероятностью 1/3 каждый. Ваш консультат наблюдает за действиями «природы» и делает свой ход, а именно сообщает вам о трех вариантах доходности инвестиций, в качестве которых снова могут выступать варианты П, С и Х. Мы сразу же немного упростим дерево игры, отметив, что у консультанта нет никаких мотивов занижать рентабельность инвестиций: он никогда не станет сообщать о типе П, если правда — С или Х, или о типе С, если на самом деле это Х. (Эти действия можно было бы оставить в дереве, но они его слишком усложнят. Применение одного шага обратных рассуждений показывает, что ни одно из этих действий не является оптимальным для консультанта, а значит, ни одно из них не может быть частью равновесия.)
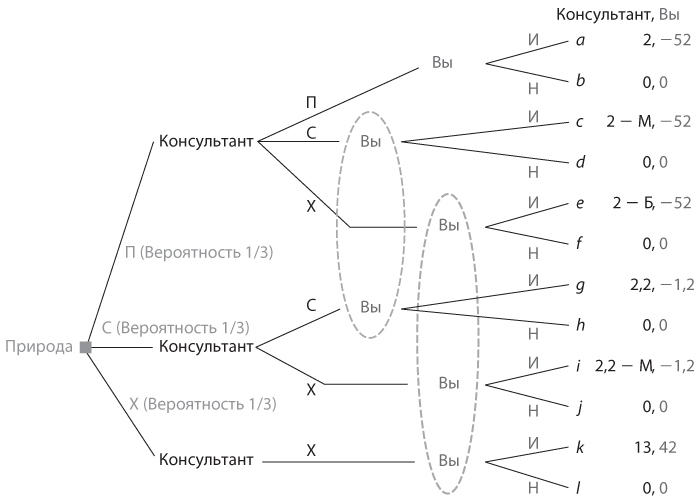
Рис. 8.5. Дерево игры с дешевым разговором между финансовым консультантом и инвестором
И наконец, вы ходите третьим и должны выбрать, инвестировать (И) или не инвестировать (Н). Однако вы не можете наблюдать за действиями «природы» непосредственно и знаете о них только со слов консультанта. Следовательно, для вас оба узла, в которых он сообщает о типе С, объединены в одно информационное множество, тогда как все три узла, в которых он сообщает тип Х, собраны в другое информационное множество (на рис. 8.5 оба информационных множества выделены пунктирными овалами). Наличие информационных множеств говорит о том, что вы ограничены в своих действиях. В том информационном множестве, где консультант сообщает тип С, вы должны сделать один и тот же выбор в отношении инвестиций в обоих узлах множества, то есть выбрать либо И, либо Н в обоих узлах, поскольку не можете провести различия между этими узлами в составе данного информационного множества, с тем чтобы выбрать И в одном узле и Н в другом. Точно так же вы должны выбрать либо И, либо Н во всех трех узлах информационного множества, в котором консультант сообщает тип Х.
В каждом концевом узле выигрыш консультанта показан первым, а ваш — вторым. Выигрыши, которые исчисляются в тысячах долларов, отражают те же числовые значения, что и в выполненном выше эвристическом анализе. Вы выплачиваете консультанту комиссионные 2% от инвестиции в размере 100 000 долларов, и ваша прибыль составляет −50, если вы инвестируете в актив типа П, 1 при инвестициях в актив типа С, и 55 — в актив типа Х. Консультант получает 20% от любой прибыли, которую вы заработаете благодаря его рекомендации. Единственное отличие данной модели от предыдущей: мы не приводим здесь точного значения репутационных издержек консультанта в случае искажения информации, а вместо этого используем символ М для обозначения репутационных издержек при незначительном искажении информации и символ Б — при значительном искажения информации. Для того чтобы привести эти параметры в соответствие с нашим анализом, мы исходим из предположения, что оба имеют положительное значение, а также что М < Б. Этот подход позволяет проанализировать оба уровня репутационных соображений, о которых шла речь выше.
В качестве примера того, как вычисляется каждая пара выигрышей, рассмотрим узел, в котором «природа» создала актив типа С, консультант сообщил о типе Х, а вы выбрали И (на этот узел обозначен символом i). При таком раскладе ваш выигрыш составляет 80% от прибыли 1 на ваши инвестиции, из которого исключаются авансовые комиссионные 2, выплаченные консультанту, что в итоге равно 0,8 – 2 = −1,2. Консультант получает комиссионные 2 и свою долю 20% от прибыли на инвестиции в данный актив (0,2), но при этом несет репутационные издержки М, а значит, его общий выигрыш будет 2,2 – М. Мы предоставляем вам возможность самостоятельно убедиться в том, что все остальные выигрыши, отображенные на данном дереве игры, вычислены правильно.
С помощью дерева игры на мы можем построить для нее таблицу выигрышей. Строго говоря, она должна включать в себя все стратегии, доступные вам и вашему консультанту. Однако, как и при построении дерева игры, мы можем исключить из рассмотрения некоторые стратегии, прежде чем вносить их в таблицу; в частности, удалим все явно плохие стратегии. Это позволит построить гораздо меньшую, а значит, и куда более удобную таблицу по сравнению с той, в которую были бы включены все возможные стратегии.
Какие стратегии мы можем исключить из рассмотрения в качестве равновесных? Ответ на этот вопрос включает два аспекта. Во-первых, мы можем игнорировать стратегии, которые однозначно не будут использованы. Во время построения дерева игры мы уже удалили некоторые из них для консультанта (например, стратегию «сообщать тип П, если истинный тип актива Х»). Теперь мы можем видеть, что у вас также есть несколько вариантов, подлежащих исключению. Например, стратегия «выбрать И, если консультант сообщает тип П» в концевом узле доминируема стратегией «выбрать Н, если консультант сообщает тип П», поэтому мы исключаем ее из рассмотрения. Точно так же в рамках информационного множества «сообщить тип С» ваша стратегия «выбрать И, если консультант сообщает тип С» доминируема стратегией «выбрать Н, если консультант сообщает тип С»; это худший выбор в обоих концевых узлах (c и g) и поэтому тоже может быть проигнорирован. Во-вторых, мы можем исключить все стратегии, не оказывающие никакого влияния на поиск равновесий дешевого разговора. Например, для консультанта обе стратегии «сообщить тип П» и «сообщить тип С» приводят к выбору вами стратегии Н, поэтому мы исключаем обе. Помимо концевых узлов, которые мы уже удалили на (a, c и g), мы можем удалить также узлы b, d и h.
После такой процедуры упрощения у нас остается всего шесть концевых узлов (e, f, i, j, k и l), соответствующих стратегиям, в случае которых консультант сообщает, что актив относится к типу Х, а вы в ответ выбираете стратегию согласно полученной информации. Если конкретно, в распоряжении консультанта осталось три интересные стратегии («всегда сообщать тип Х независимо от того, каков истинный тип актива — П, С или Х», «сообщать тип Х только в случае, если истинный тип актива С или Х» и «сообщать Х только в случае, если и только если истинный тип актива Х»), а в вашем — две («выбрать И, если консультант сообщает тип Х» и «выбрать Н, если консультант сообщает тип Х»). Эти пять стратегий позволяют построить таблицу выигрышей три на два, представленную на рис. 8.6.

Рис. 8.6. Таблица выигрышей игры с дешевым разговором
Выигрыши по каждой комбинации стратегий на рис. 8.6 — это ожидаемые выигрыши, вычисленные с помощью значений в концевых узлах дерева (которых можно достичь при данной комбинации стратегий), взвешенных по соответствующим вероятностям. В качестве примера рассмотрим верхнюю левую ячейку таблицы, в которой консультант сообщает о том, что актив относится к типу Х независимо от его истинного типа. Эта комбинация стратегий приводит к концевым узлам e, i и k, каждый с вероятностью 1/3. Следовательно, ожидаемый выигрыш консультанта в этой ячейке составляет {[1/3 × (2 – Б)] + [1/3 × (2,2 – М)] + (1/3 × 13)} = 1/3 × (17, 2 – Б – М). Точно так же ваш ожидаемый выигрыш в той же ячейке равен [(1/3 × –52) + (1/3 × –1,2) + (1/3 × 42)] = 1/3 × (–11,2). Мы снова предоставляем вам возможность самостоятельно убедиться в том, что оставшиеся ожидаемые выигрыши рассчитаны правильно.
Теперь, имея полную таблицу выигрышей, мы можем использовать представленные в методы для поиска равновесия с оговоркой, что значения М и Б в нашем анализе играют определенную роль. Простой анализ наилучших ответов показывает, что ваш наилучший ответ на стратегию консультанта «всегда Х» — «Н, если Х», а на две его другие стратегии — «И, если Х». Аналогичным образом, наилучшим ответом консультанта на вашу стратегию «Н, если Х» может быть любая из его трех стратегий. Таким образом, мы имеем первый результат: верхняя правая ячейка — это всегда равновесие Нэша. Если консультант сообщает, что актив относится к типу Х, каким бы ни был его истинный тип (или, если уж на то пошло, отправляет любое сообщение, но только одно и то же во всех трех сценариях), вам лучше выбрать Н, а если вы выбираете Н, у консультанта нет причин отклоняться от своего выбора. Это и есть равновесие пустого разговора при полном отсутствии обмена информацией, с которым мы уже сталкивались выше.
Далее рассмотрим наилучший ответ консультанта на ваш выбор стратегии «И, если Х». Единственно возможные равновесия возникают, когда он применяет стратегию «Х, только если С или Х» или «Х, если и только если Х». Однако какой именно из двух вариантов он выберет (или не выберет ни одного их них), зависит от конкретных значений Б и М. Для того чтобы пара стратегий {«Х, только если С или Х», «И, если Х»} была равновесием Нэша, должны выполняться следующие условия: 15,2 – М > 17,2 – Б – М и 15, 2 – М > 13. Первое выражение верно, если Б > 2, второе — если М < 2,2. Таким образом, если значения Б и М удовлетворяют этим условиям, средняя левая ячейка будет равновесием дешевого разговора (по Нэшу). В этом равновесии сообщение консультанта о типе актива Х не позволяет вам определить, каков истинный тип, С или Х, но вы точно знаете, что это не П. Располагая такой информацией, вы можете быть уверены, что ваш ожидаемый выигрыш будет положительным, и решаете инвестировать. В этой ситуации Х действительно означает «не-П», а равновесный исход формально эквивалентен равновесию с частичным раскрытием информации, о котором мы говорили выше.
Мы можем также проверить выполнение условий, при которых пара стратегий {«Х, если и только если Х», «И, если Х»} — это равновесие Нэша. Такой исход требует, чтобы 13 > 17,2 – Б – М и 13 > 15, 2 – М. Проанализировать эти выражения не так легко, как представленные выше. Однако следует отметить, что второе выражение требует, чтобы М > 2,2, а также что мы предположили, что Б > М; следовательно, условие Б > 2,2 должно выполняться при выполнении условия М > 2,2. Теперь можете использовать эти условия для проверки выполнения первого выражения. Возьмите минимальное значение Б и М, равное 2,2, и подставьте его в выражение 13 > 17,2 – Б – М, в результате получите 13 > 12,8, что, безусловно, верно. Эти расчеты указывают на то, что нижняя левая ячейка — это равновесие дешевого разговора, когда М > 2,2, при условии, что Б > М. Это и есть равновесие с полным раскрытием информации, которое мы нашли в конце предыдущего анализа.
В каждом из описанных случаев наряду с равновесиями {«Х, только если С или Х», «И, если Х»} и {«Х, если и только если Х», «И, если Х»} существует равновесие пустого разговора. Обратите внимание, что мы получим только равновесие пустого разговора в случае низких репутационных издержек консультанта (Б < 2 и М < Б), что согласуется со сформулированными ранее интуитивными выводами. И наконец, если мы ограничим язык передаваемых сообщений более грубым разбиением на П и «не-П», то продолжение представленного здесь анализа покажет, что множество стратегий {«не-П, если С или Х», «И, если не-П»} также будет равновесием Нэша в данной игре.
В каждом случае наш формальный анализ подтверждает аргументы, приведенные в . Некоторые из вас могут посчитать вербальный подход достаточным для большинства, если не для всех своих потребностей. Другие отдадут предпочтение более формальной модели, представленной в данном разделе. Однако вы должны осознавать, что деревья и таблицы имеют свои ограничения: как только ваша модель станет достаточно сложной (например, будет включать в себя непрерывный диапазон вариантов сообщений), вам придется практически полностью положиться на математику для поиска равновесий. Способность решать модели с асимметричной информацией в различных формах (вербально, посредством деревьев и таблиц или с помощью алгебры или исчисления) — очень важный навык. Ниже мы приведем дополнительные примеры таких игр; при этом одни из них будут решены путем сочетания интуиции и алгебры, а другие — с помощью дерева игры и таблицы выигрышей. Во всех случаях один метод решения не исключает другой, поэтому вы можете попробовать самостоятельно применить альтернативные варианты решения.
4. Неблагоприятный отбор, сигнализирование и скрининг
А. Неблагоприятный отбор и несостоятельность рынка
Во многих играх один из участников знает об исходе игры нечто такое, что неизвестно другим. Работодатель знает о квалификации потенциального сотрудника гораздо меньше, чем сам сотрудник; еще труднее отслеживать более неопределенные, но важные качества сотрудника, такие как отношение к работе и умение работать в коллективе. Страховой компании гораздо меньше известно о состоянии здоровья или навыках вождения человека, подающего заявку на оформление медицинской страховки или автострахования, чем самому страхователю. Продавец подержанного автомобиля многое о нем знает благодаря длительной эксплуатации, а потенциальный покупатель может в лучшем случае получить минимум информации в ходе осмотра авто.
В таких ситуациях непосредственная коммуникация не обеспечивает достоверной передачи информации. Неквалифицированные работники заявляют о наличии определенных навыков, чтобы получить более высокооплачиваемую должность; люди, которые относятся к категории повышенного риска, утверждают, что у них крепкое здоровье или хорошие навыки вождения, чтобы выплачивать более низкие страховые взносы; владельцы плохих автомобилей утверждают, что их автомобили работают прекрасно и за долгие годы не создавали никаких проблем. Другие стороны подобных сделок знают о наличии стимулов к искажению истины и не доверяют информации, передаваемой на словах. Следовательно, в этих играх нет условий для формирования равновесия дешевого разговора, о котором шла речь в .
Но что происходит, если менее информированные стороны таких сделок вообще не имеют возможности получить соответствующую информацию? Другими словами, выражаясь в терминах, введенных в , в их распоряжении нет ни достоверных инструментов скрининга, ни сигналов. Если страховая компания предлагает страховой полис, который обходится в 5 центов за каждый доллар страхового покрытия, он будет особенно привлекателен для людей, которые знают, что их собственный риск (болезни или автомобильной аварии) превышает 5%. Безусловно, некоторые люди, знающие о том, что их риск ниже 5%, все равно купят такой страховой полис ввиду нерасположенности к риску. Однако в общей совокупности лиц, претендующих на оформление этого страхового полиса, доля лиц с более высокой степенью риска превысит долю лиц с аналогичным риском в общей численности населения. Таким образом, страховая компания выборочно привлекает невыгодную, или неблагоприятную, группу клиентов. Данный феномен известен как неблагоприятный отбор и характерен для сделок с асимметричной информацией. (На самом деле этот термин возник именно в страховой отрасли.)
Потенциальные последствия неблагоприятного отбора для рыночных сделок весьма наглядно продемонстрировал Джордж Акерлоф в статье, которая положила начало экономическому анализу ситуаций с асимметричной информацией и обеспечила ему Нобелевскую премию в 2001 году. Мы приводим этот пример, чтобы ознакомить вас с возможными последствиями неблагоприятного отбора.
Б. Рынок «лимонов»
Представьте себе сформировавшийся в 2014 году рынок определенного типа подержанных автомобилей, скажем Citrus 2011 года выпуска. Предположим, что в эксплуатации эти машины оказались либо безотказными и надежными, либо очень проблемными. Автомобили второго типа принято называть «лимонами», поэтому для контраста назовем автомобили первого типа «апельсинами».
Допустим, каждый владелец «апельсина» Citrus оценивает его в 12 500 долларов и готов с ним расстаться за более высокую, но не более низкую цену по сравнению с этой ценой. В свою очередь, каждый владелец «лимона» Citrus оценивает его в 3000 долларов. Предположим, потенциальные покупатели готовы заплатить больше указанных сумм. Если бы покупатель был уверен, что приобретаемый им автомобиль — «апельсин», он бы выложил за него 16 000 долларов; если бы он знал, что автомобиль — «лимон», то 6000 долларов. Поскольку покупатели оценивают автомобили каждого типа по более высокой цене, чем их непосредственные владельцы, продажа авто была бы взаимовыгодной. Цена «апельсина» могла бы варьироваться в диапазоне от 12 500 до 16 000 долларов, а «лимона» — от 3000 до 6000 долларов. Для определенности допустим, что количество таких автомобилей ограниченно, а потенциальных покупателей больше, чем машин. Тогда покупатели, конкурируя друг с другом, повысят цену автомобилей до максимальной, которую они готовы заплатить, то есть «апельсин» будет стоить 16 000 долларов, а «лимон» — 6000 долларов при условии стопроцентной идентификации типа каждого из них.
Однако информация о качестве любого конкретного автомобиля несимметрично распределена между двумя сторонами сделки. Владелец Citrus точно знает, «апельсин» это или «лимон», а потенциальный покупатель — нет, и владельцу «лимона» абсолютно невыгодно обнародовать такие сведения. Давайте пока ограничимся анализом рынка частных подержанных автомобилей, на котором законы, требующие правдивого раскрытия информации, либо не действуют, либо трудновыполнимы. Кроме того, будем исходить из того, что у потенциального покупателя отсутствует любая возможность заметить нечто такое, что поможет ему определить тип автомобиля; точно так же и владелец автомобиля лишен возможности указать его тип. Таким образом, в данном примере мы проанализируем только последствия асимметричности информации, когда обе стороны сделки не могут воспользоваться инструментами сигнализации или скрининга.
Когда покупатели не могут отличить «апельсины» от «лимонов», на рынке не может быть разных цен на автомобили этих типов. Цена на автомобиль Citrus должна быть только одна — p, а значит, два типа автомобилей, «апельсины» и «лимоны», следует объединить в одну группу. Возможна ли эффективная торговля при таких обстоятельствах — зависит от доли «апельсинов» и «лимонов» в общей совокупности авто. Предположим, доля «апельсинов» — f от подержанных автомобилей Citrus, а «лимонов» — оставшаяся часть (1 – f).
Несмотря на то что покупатели не могут проверить качество отдельного автомобиля, они могут знать долю хороших машин в общей совокупности авто, например, из газет; мы предполагаем, что в действительности так и происходит. Если на продажу выставляются все автомобили, потенциальный покупатель может рассчитывать на случайный выбор с вероятностями получения «апельсина» и «лимона» f и (1 – f) соответственно. Ожидаемое значение цены автомобиля составляет 16 000 × f + 6000 × (1 – f) = 6000 + 10 000 × f > p. Потенциальный покупатель приобретет такой автомобиль, если его ожидаемая стоимость превысит цену, которую ему предлагают заплатить, то есть если 6000 + 10 000 × f > p.
Теперь проанализируем эту ситуацию с точки зрения продавца. Владельцы знают, какие у них автомобили — «апельсины» или «лимоны». Владелец «лимона» готов его продать, если цена превышает для него ценность автомобиля, то есть если p > 3000. Однако владелец «апельсина» требует, чтобы p > 12 500. Если это условие владельца «апельсина» удовлетворяется, то удовлетворяются и условия владельца «лимона».
Таким образом, для выполнения условий всех покупателей и продавцов, чтобы они были готовы заключить сделку, нужно, чтобы 6000 + 10 000 × f > p > 12 500. Если доля «апельсинов» в общей совокупности удовлетворяет условию 6000 + 10 000 × f > 12 500, или f > 0,65, можно найти цену, которая позволит выполнить эту задачу, в противном случае эффективная торговля невозможна. При 6000 + 10 000 × f < 12 500 (если исключить редкий и маловероятный случай равенства между этими двумя вариантами) владельцы «апельсинов» не захотят продавать их по максимальной цене, которую готовы заплатить потенциальные покупатели. В результате в совокупности подержанных автомобилей, выставленных на продажу, будет наблюдаться неблагоприятный отбор и «апельсины» вообще не появятся на рынке. Потенциальные покупатели, понимая, что они наверняка получат «лимон», будут готовы платить не более 6000 долларов. Владельцы «лимонов» будут довольны таким исходом, и «лимоны» будут продаваться. Однако в связи с асимметричностью информации рынок «апельсинов» рухнет. Этот исход станет одним из вариантов закона Грешема, в котором плохие автомобили вытесняют хорошие.
Поскольку отсутствие информации делает невозможным получение обоснованной цены на «апельсины», их владельцам каким-то способом понадобится убедить покупателей, что у них хорошие автомобили. Другими словами, им необходимо подать сигнал о типе автомобиля. Проблема в том, что владельцы «лимонов» тоже захотят сделать вид, будто их автомобили — «апельсины», и с этой целью могут имитировать большинство сигналов, подаваемых владельцами «апельсинов». Майкл Спенс, сформулировавший концепцию сигнализирования и разделивший с Акерлофом и Стиглицем Нобелевскую премию 2001 года за работу в области экономической информации, описывает проблемы владельцев «апельсинов» в своей новаторской книге о сигнализировании так: «Вербальные (словесные) заявления ничего не стоят, а значит, они бесполезны. Кто угодно может солгать о том, почему он продает машину. Кто угодно может предложить покупателю проверить состояние автомобиля. Владелец “лимона” также может сделать такое предложение. Это блеф. В любом случае он ничего не теряет. Кроме того, такие проверки дорогостоящи, а заключение о надежности автомобиля, сделанное механиком владельца, не заслуживает доверия. Умный владелец автомобиля, который не относится к числу “лимонов”, мог бы заплатить за техосмотр, но предоставить покупателю возможность выбрать эксперта. В таком случае у владельца возникает другая проблема — максимально сократить затраты на техосмотр. Никаких гарантий нет. Продавец может уехать в Кливленд, не оставив адреса».
На самом деле ситуация не столь безнадежна, как обрисовал Спенс. Люди и компании, занимающиеся продажей подержанных автомобилей, могут заслужить репутацию честных партнеров и извлекать из нее выгоду, устанавливая надбавку к цене продаваемых автомобилей. (Безусловно, некоторые торговцы подержанными автомобилями поступают непорядочно.) Одни покупатели разбираются в автомобилях, другие приобретают их у знакомых, а значит, могут проверить историю машины. Кроме того, автодилеры могут предлагать покупателям гарантию — эту тему мы рассмотрим подробнее ниже. А на других рынках недобросовестным игрокам труднее имитировать действия добросовестных, поэтому достоверное сигнализирование возможно. Конкретным примером может служить ситуация, в которой образование выступает в качестве сигнала о квалификации. В подобной ситуации людям с низким уровнем квалификации труднее получить такое образование, которое бы позволило ошибочно принять их за высококвалифицированных специалистов. Для того чтобы по уровню образования провести различие между типами специалистов, необходимо выполнение следующего условия: получение образования должно обходиться неквалифицированным работникам гораздо дороже, чем квалифицированным. Для того чтобы продемонстрировать, как и когда сигнализирование может эффективно разделить типы игроков, давайте обратимся к рынку труда.
В. Сигнализирование и скрининг: типичные ситуации
Основная идея использования сигнализирования или скрининга для передачи или сбора информации очень проста: игроки разных типов (то есть владеющие разной информацией о собственных характеристиках или об игре и выигрышах в ней в более общем случае) должны считать оптимальным выполнение различных действий так, чтобы они правдиво раскрывали их истинный тип. Существует множество ситуаций с такой асимметричностью информации, а также стратегий сигнализирования и скрининга, позволяющих справиться с подобными задачами. Ниже описывается ряд ситуаций, в которых применимы методы анализа, представленные в данной главе.
I.-Страхование. Потенциальные покупатели страховых полисов относятся к разным категориям риска, или степени их риска для страховой компании. Например, среди многих водителей, подающих заявки на оформление полисов страхования автотранспортных средств на случай столкновения, есть как более, так и менее осторожные. Каждый потенциальный клиент лучше, чем страховая компания, знает о том, к какой категории риска он принадлежит. С учетом условий того или иного страхового полиса компания заработает меньше прибыли (или понесет более крупные убытки) на страховании клиентов более высокой категории риска. Тем не менее данный страховой полис может оказаться более привлекательным именно для клиентов с повышенным уровнем риска. Таким образом, страховая компания привлекает менее благоприятную группу клиентов, а значит, происходит неблагоприятный отбор. Безусловно, страховая компания заинтересована в проведении различия между категориями риска. Это можно сделать посредством одного из инструментов скрининга.
Предположим, существуют только две категории риска. Следовательно, страховая компания может предложить два полиса страхования, из которых каждый клиент выберет какой-то один. Первый полис предусматривает более низкий страховой взнос (измеряемый в определенном количестве центов на каждый доллар страхового покрытия), но обеспечивает покрытие меньшего процента от понесенных клиентом убытков. Второй полис предусматривает более высокий страховой взнос, но обеспечивает и более высокий процент страхового покрытия убытков, возможно, даже 100 процентов. (При страховании на случай столкновения эти убытки представляют собой стоимость ремонта автомобиля в автомастерской.) Клиент, принадлежащий к более высокой категории риска, с большей вероятностью может понести непокрытые убытки, поэтому он гораздо охотнее заплатит более высокий страховой взнос, чтобы получить большее страховое покрытие. Исходя из этого, страховая компания может установить соотношение между размером страховых взносов и покрытия убытков таким образом, чтобы клиенты более высокой категории риска выбирали полисы с высокими взносами и высоким покрытием, а клиенты более низкой категории риска — полисы с более низкими взносами и низким страховым покрытием. При наличии других категорий риска страховой компании необходимо предлагать потенциальным клиентам больше полисов страхования; в случае непрерывного диапазона категорий риска может быть и соответствующий диапазон страховых полисов.
Безусловно, любая страховая компания вынуждена бороться за каждого клиента. Такая конкуренция влияет на условия пакетов страховых взносов и уровней покрытия, предлагаемых страховой компанией. Иногда конкуренция может даже препятствовать достижению равновесия, поскольку каждое предложение рискует проиграть в противостоянии с другим предложением. Однако общая идея, лежащая в основе создания полисов с дифференцированными страховыми взносами для клиентов разных категорий риска, обоснованна и важна.
II.-Гарантия. Многие типы товаров длительного пользования, такие как автомобили, компьютеры и стиральные машины, отличаются по уровню качества. Любая компания-производитель имеет полное представление о своем продукте. А вот потенциальные покупатели менее информированны. Может ли компания, которая знает, что ее продукт отличается высоким качеством, подать об этом потенциальным покупателям достоверный сигнал?
Самый очевидный и наиболее распространенный сигнал — гарантия. Стоимость гарантии действительно высококачественного продукта ниже, поскольку его производитель реже сталкивается с требованиями о ремонте или замене, чем производитель некачественного продукта. Следовательно, гарантия может служить сигналом о высоком качестве изделия, а покупатели интуитивно учитывают этот факт, принимая решение о покупке.
Как правило, в таких ситуациях сигнал должен быть избыточным, с тем чтобы его имитация обходилась достаточно дорого. В связи с этим компания, выпускающая качественные автомобили, должна предлагать весьма серьезную гарантию, для того чтобы подать достоверный сигнал о качестве автомобиля. Это требование имеет особое значение для любой компании-новичка в отрасли, еще не заслужившей репутации производителя высококачественной продукции. Например, Hyundai вышла на рынок США в 1986 году и на протяжении первых десяти лет имела репутацию компании, выпускающей автомобили низкого качества. В середине 1990-х Hyundai инвестировала большие средства в улучшение технологии, дизайна и производственного процесса. Для того чтобы обновить сложившийся имидж, компания предложила революционную на то время гарантию на свои автомобили, рассчитанную на 10 лет и 100 000 миль пробега. Теперь организации по защите потребителей считают Hyundai одним из лучших производителей высококачественных автомобилей.
III.-Ценовая дискриминация. Покупатели большинства продуктов неоднородны с точки зрения готовности платить, уделять время поиску более выгодной цены и т. д. Компании хотели бы найти способ идентифицировать потенциальных клиентов с более высокой готовностью платить, чтобы назначать им одну, предположительно обоснованно высокую цену, и в то же время выборочно делать выгодные предложения тем клиентам, которые не могут платить так много (до тех пор, пока их готовность платить все же превышает затраты на поставку соответствующего продукта). Компании могут успешно устанавливать разные цены для разных групп потребителей с помощью инструментов скрининга для разделения типов клиентов. Мы обсудим такие стратегии, которые известны в экономической литературе как ценовая дискриминация, подробнее в . Здесь же представим лишь краткий обзор этой темы.
Наиболее показательный пример дискриминационных цен относится к отрасли авиаперевозок. Пассажиры, предпочитающие совершать деловые поездки бизнес-классом, зачастую готовы платить за авиабилеты больше, чем туристы, потому что как минимум часть их стоимости возмещает работодатель. Со стороны авиакомпании было бы незаконно открыто выяснять тип каждого пассажира и назначать разные цены пассажирам разных типов. Однако авиакомпании успешно используют тот факт, что туристы предпочитают составлять маршрут путешествий заранее, тогда как бизнес-пассажирам необходимо сохранять определенную гибкость в своих планах. В связи с этим авиаперевозчики устанавливают разные цены на билеты, подлежащие и не подлежащие возврату, и предоставляют путешественникам самим выбирать тип тарифа. Такая стратегия ценообразования представляет собой пример скрининга посредством самоотбора. Другие инструменты — специальный тариф при условии предварительной покупки билета, требование о минимальном сроке пребывания в ночь с субботы на воскресенье, разные категории обслуживания на борту (первый класс, бизнес-класс и экономкласс) — также применяются в целях скрининга.
Ценовая дискриминация характерна не только для таких дорогостоящих вещей, как авиабилеты. Другие схемы дискриминационного ценообразования можно наблюдать на многих рынках, где цены гораздо ниже цен на воздушные перевозки. Например, кафе и закусочные обычно предлагают завсегдатаям дисконтные карты, обеспечивающие скидку на кофе или закуски. Это объясняется тем, что постоянные клиенты в большей степени готовы искать более выгодные предложения поблизости, тогда как приезжие или случайные посетители идут в первое попавшееся кафе или закусочную и не тратят время на поиск заведения с более низкими ценами. Завышенная обычная цена и скидка в виде бесплатного одиннадцатого заказа — и есть то меню вариантов, из которого выбирают два типа клиентов, что, собственно, и разделяет их на типы.
Книги — еще один пример. Как правило, сначала книги издаются в твердом переплете; более дешевый вариант в мягкой обложке выходит спустя несколько месяцев, а то и через год и даже позже. Разница между затратами на публикацию двух версий книги несущественна. Но эти версии служат для разделения покупателей на тех, которые хотят прочитать книгу сразу же и готовы платить больше за возможность это сделать, и тех, кто намерен ждать дольше, чтобы заплатить меньше.
IV.-Дизайн и реклама продукта. Может ли привлекательный, хорошо продуманный внешний вид продукта служить сигналом о его высоком качестве? Основное условие сводится к тому, что затраты на разработку такого сигнала для компании, которая лишь создает видимость высокого качества, должны быть существенно выше, чем для компании, выпускающей действительно качественный продукт. Как правило, затраты на внешнее оформление продукта не зависят от его качества. Следовательно, подражатель не сталкивается с разницей в затратах, а значит, такой сигнал не будет достоверным.
Однако порой подобные сигналы могут иметь под собой определенное обоснование. Внешнее оформление продукта требует фиксированных затрат, которые распределяются на весь его жизненный цикл. Покупатели действительно узнают о качестве продукта из собственного опыта, от друзей, а также из обзоров и отзывов в СМИ. Эти факторы указывают на то, что товар высокого качества может рассчитывать на более длительный период пребывания на рынке и более высокий общий объем продаж. Стало быть, затраты на дорогостоящее внешнее оформление распределяются на большее количество выпущенной продукции и в меньшей степени увеличивают себестоимость каждой единицы продукта, если он имеет более высокое внутреннее качество. Фактически компания делает такое заявление: «У нас хороший продукт, и мы его продадим в большом количестве. Поэтому мы можем себе позволить потратить столько денег на его дизайн. Такие затраты были бы непомерными для компании-однодневки, которая рассчитывает продать не так уж много единиц продукта, прежде чем люди обнаружат его низкое качество и перестанут покупать». Даже дорогостоящий, на первый взгляд бесполезный и неинформативный запуск продукта и рекламная кампания способны обеспечить аналогичный результат сигнализирования.
Похожая ситуация складывается и в банках. Когда вы заходите в банк и видите добротные мраморные стойки и бархатную мебель, это может убедить вас в его стабильности. Однако чтобы этот сигнал действительно работал, важно, чтобы здание, мебель и внутренняя отделка носили индивидуальный характер и были присущи именно этому банку. Если все это можно без труда продать учреждениям других типов и превратить помещение, скажем, в ресторан, то не заслуживающий доверия владелец мог бы имитировать поистине надежный банк без всяких дополнительных затрат. В данной ситуации такой сигнал был бы недостоверным.
V.-Такси. Приведенные выше примеры взяты в основном из экономики, а теперь давайте рассмотрим пример из области социологии, касающийся службы такси. Подавляющее большинство людей, нанимающих такси, просто хотят доехать до пункта назначения, заплатить за проезд и уйти. Однако некоторые пытаются ограбить таксиста или угнать его автомобиль, возможно, даже применив физическое насилие. Как таксисты могут осуществить скрининг потенциальных клиентов и предоставлять услуги только хорошим людям? Социологи Диего Гамбетта и Хезер Хэмилл проанализировали этот вопрос на основании многочисленных бесед с таксистами в Нью-Йорке (где грабежи — большая проблема) и Северной Ирландии (где в период проведения исследования серьезной проблемой были межрелигиозные конфликты).
Водителям необходим подходящий инструмент скрининга, поскольку они знают, что потенциальные клиенты с плохими намерениями пытаются имитировать действия хороших клиентов. Здесь также применимо условие о разнице в затратах. Нет никаких гарантий того, что житель Нью-Йорка в добротном костюме не представляет опасности, так как грабитель может купить и надеть костюм по той же цене, что и хороший клиент. Расу и пол тоже нельзя использовать для отсеивания клиентов. В Северной Ирландии враждующие группировки также трудноотличимы по внешним характеристикам.
Гамбетта и Хэмилл обнаружили, что некоторые инструменты скрининга более приемлемы для таксистов. Например, заказ такси по телефону — более достоверный сигнал о благонадежности клиента, чем попытки поймать такси на улице: когда вы указываете место, где вас должно забрать такси, служба такси в буквальном смысле знает, где вы живете. Еще важнее то, что некоторые инструменты сигнализирования оказались более эффективны для клиентов (а значит, и выступали в качестве более эффективных инструментов скрининга) при использовании в сочетании друг с другом, а не по отдельности. Ношение костюма само по себе не было достоверным инструментом скрининга, но когда человек в костюме выходил из офисного здания, таксисты считали его более безопасным клиентом, чем человека в костюме, стоящего на углу улицы. В настоящее время в вестибюлях большинства офисных зданий есть охрана, поэтому можно считать, что такой клиент уже прошел один уровень проверки системой безопасности.
Пожалуй, самыми важными оказались бессознательные сигналы, подаваемые людьми (микровыражения лица, жесты и т. д.), которые опытные таксисты умеют читать и интерпретировать. Именно ввиду непроизвольности таких сигналов их имитация потребовала бы невероятных усилий, а значит, они могут считаться самыми эффективными инструментами скрининга, необходимого для разделения типов клиентов.
VI.-Политические бизнес-циклы. Теперь приведем еще два примера из области политэкономии. Действующие правительства часто увеличивают бюджетные расходы, чтобы обеспечить рост экономики накануне выборов, тем самым надеясь привлечь больше голосов избирателей и выиграть выборы. Но разве не должны рационально мыслящие избиратели разгадать эту уловку и понять, что сразу же после завершения выборов правительство будет вынуждено сократить расходы, что может привести к экономическому спаду? Для того чтобы расходы накануне выборов эффективно сигнализировали о типе, избиратели должны испытывать неопределенность в отношении типа правительства в плане его компетентности. Будущая рецессия повлечет за собой определенные политические издержки для правительства. И они будут меньше, если правительство более компетентно в вопросах экономики. Когда разница в издержках между компетентным и некомпетентным правительством достаточно большая, значительное увеличение расходов может выступать в качестве достоверного сигнала о компетентности.
Еще один пример относится к методам управления инфляцией. Многие страны в разные времена переживали периоды высокой инфляции, и их правительства благочестиво заявляли о своем намерении снизить ее уровень. Может ли правительство, которое действительно заботится о стабильности цен, достоверно подать сигнал о своем типе? Да. Правительства могут выпустить облигации, защищенные от инфляции, процентная ставка по которым автоматически повышается с повышением темпов инфляции или капитальная стоимость которых увеличивается пропорционально росту уровня цен. Выпуск государственных долговых обязательств в такой форме обходится правительству, отдающему предпочтение политике, приводящей к росту инфляции, дороже, поскольку ему приходится выплачивать более высокий процент или увеличивать сумму своего долга. Следовательно, правительство с подлинно антиинфляционной политикой может выпустить защищенные от инфляции облигации в качестве достоверного сигнала, отделяя себя тем самым от типа правительства, предпочитающего инфляцию.
VII.-Эволюционная биология. И в заключение — пример из области естественных наук. У многих видов птиц у самцов очень яркое и тяжелое оперение, которое привлекает самок. Казалось бы, самки должны искать генетически более развитых самцов, с тем чтобы увеличить шансы потомства дожить до зрелости и, в свою очередь, привлечь партнера. Но почему яркое оперение указывает на наличие данных генетических качеств? На первый взгляд может показаться, что такое оперение — недостаток, поскольку делает самца более заметным для хищников (и охотников) и менее мобильным, а значит, и в меньшей степени способным спастись. Почему же самки выбирают, казалось бы, столь неполноценных самцов? Ответ связан с условиями достоверного сигнализирования. Хотя тяжелое оперение — действительно физический недостаток, он все же говорит о том, что у самца с подобным оперением генетически более развиты такие качества, как сила и скорость. Чем слабее самец, тем труднее ему вырастить и поддерживать качественное оперение. Следовательно, именно тяжесть оперения делает его достоверным сигналом о качестве самца.
Г. Экспериментальные данные
Определение характеристик и поиск равновесий в играх с сигнализированием и скринингом предполагает использование ряда достаточно тонких концепций и вычислений. В частности, в каждом из приведенных выше примеров формальные модели должны быть тщательно описаны для того, чтобы можно было сформулировать обоснованные и точные прогнозы в отношении выбора игроков. В таких играх участникам следует пересматривать или обновлять значения вероятностей, присваиваемые ими типу (типам) игроков на основании наблюдений за их действиями. Это обновление требует применения теоремы Байеса, которая описана в . Кроме того, в мы подробно проанализируем игру, нуждающуюся в подобном обновлении.
Даже не вдаваясь в детали, вы можете себе представить, что вычисления для обновления вероятностей достаточно сложны. Стоит ли ожидать, что игроки смогут выполнить их правильно? Существует немало доказательств того, что люди очень плохо справляются с вычислениями, включающими вероятности, и еще хуже — с вычислением вероятностей с учетом новой информации. Поэтому нам следует с вполне обоснованным недоверием относиться к равновесиям, зависящим от выполнения таких вычислений.
В связи с этим весьма обнадеживают выводы экономистов, которые проводили лабораторные эксперименты с сигнальными играми. Некоторые чрезвычайно тонкие уточнения байесовского равновесия Нэша и совершенного байесовского равновесия можно изучить с помощью наблюдений, хотя эти уточнения требуют не только обновления информации посредством отслеживания действий на равновесном пути, но и принятия решения о том, как можно логически вывести информацию из неравновесных действий, которые вообще не следовало бы предпринимать. Тем не менее результаты всех этих исследований не позволяют сделать однозначные выводы, поскольку многое зависит от мелких деталей организации эксперимента в лаборатории.

