26
Опять же, очень мало измерений

Вам интересно узнать, как живется в четвертом измерении, но не уверены, где его искать? Не переживайте. Никто не может видеть более чем в трех измерениях. Мы можем говорить о других измерениях, делать в них расчеты и описывать некоторые свойства, которыми они могли бы обладать, но, как бы мы ни напрягали наш мысленный взор, мы не можем их представить. (В одном из эпизодов была фраза, которую позже не включили, где Шелдон презрительно восклицает: «Я вас умоляю! Я могу представить 26 измерений. Неужели вы думаете, у меня не получится водить машину в трех?»  Возможно, он может составить концепцию 26 измерений, но как можно быть уверенным, что он их на самом деле визуализирует?) И это абсолютно нормально. Весь наш опыт приобретен в родном трехмерном измерении, и нам трудно представить то, что мы никогда не испытывали.

Измерение – это не место, это направление, непрерывная величина, база для выражения разделения между вещами. Используя три пространственных измерения, мы можем измерить разделение между точками (например, в одной миле на восток и двух милях на север, в трех милях под землей). Добавив время, мы можем измерить разделение между событиями (например, четыре секунды после восхода солнца). Вот почему время иногда называется «четвертым измерением».

Когда Шелдон использует прямоугольную систему координат (0, 0, 0, 0), чтобы обозначить момент, когда он впервые сел на свое «место», он говорил о событии, чья позиция – (0, 0, 0) и время – (. . ., 0), с которого он ведет отсчет всего .

Но это определение работает, только если он сидит неподвижно. В буквальном смысле этого слова. Теория относительности Эйнштейна основана на наблюдении, что, когда два предмета находятся в движении по отношению друг к другу, пространство и время переплетаются. (По отношению друг к другу… относительность… видите, что тут провернул Эйнштейн? И теперь вы знаете, почему она так называется.) Вместо (только) трех измерений пространства и (только) одного времени мы вынуждены говорить о четырех пространственно-временных измерениях.

Пространственно-временное измерение труднее представить, чем просто пространственное или временное, и что еще хуже, некоторые модели Вселенной требуют десять, одиннадцать или даже двадцать шесть пространственно-временных измерений. Не важно, что никто не может визуализировать все эти измерения; в них нуждаются теории – иначе не сойдутся расчеты. Поэтому, если Шелдон захотел бы дать полные координаты Исторического Момента Первого Сидения, он должен был продекламировать гораздо больше нулей. (Порадуемся, что он этого не сделал.)

Но давайте временно отделим пространство от времени – пожалуйста, посидите немного не шевелясь – и давайте поговорим о каком-нибудь четвертом пространственном измерении. Не об определенном четвертом измерении, а о каком-нибудь из них. Три пространственных измерения, одно временное, а теперь еще одно пространственное? Почему? Потому что физика природы предполагает, что существует больше измерений, чем мы способны разглядеть. (Да, это расстраивает так же, как огорчается ребенок, который только научился считать, а ему сказали, что еще есть числа меньше нуля. Как может быть меньше, чем ничего? Как может существовать направление, в котором невозможно посмотреть?)

Представьте себе абсолютно плоскую стену из бетонных плит с нарисованной на ней точкой. Чтобы дать координаты любой точки на стене по отношению к этой точке, мы можем измерить расстояние по прямой между ними и записать ориентацию этой линии. Можно говорить о точке, которая находится в трех футах на линии, которая проходит от первоначальной точки под углом в десять градусов над горизонталью. Этих двух кусочков информации – расстояние и ориентация – достаточно, чтобы четко определить местонахождение одной точки.

Другой метод, настолько же эффективный и, возможно, требующий меньше слов, – это использование правильной сетки, которую создали сами бетонные блоки. Вы могли бы сказать, например, что точка находится в пяти плитах влево от исходной точки и в двух плитах вверх. Это сочетание направлений описывает только одну возможную точку, опять же, очень четко.

Более того, если блоки выложены правильной сеткой, не важно, прямоугольные ли они или параллельны полу. Вы можете так же просто четко определить любую точку на стене, построенной из ромбовидных блоков или просто стоящих под уклоном.

Системы определения позиции с помощью углов и расстояний и система двух расстояний очень распространены. Вы сами выбирайте, какая вам подходит больше.

Прямоугольная система координат – расстояние в двух направлениях – хорошо работает для путешествия по городу на машине. В море или в воздухе более естественно использовать полярную систему координат: радиус (дальность) плюс угол (угол на огромном воображаемом круге).

Есть еще более экзотические сочетания, которые объединяют круги полярных координат с двумя расстояниями прямоугольной системы. На Гавайях обычно объясняют дорогу, давая расстояние вдоль (изогнутого) берега плюс расстояние вглубь острова или в сторону океана.

Манхэттен известен своей прямоугольной сеткой, Токио – своими кольцевыми дорогами. Но прямоугольная и полярная системы координат – это не все способы, которыми можно найти местоположение в двух измерениях, и диагональные улицы Чикаго тому доказательство.

Большинство улиц в Чикаго расположены в сетке север-юг-восток-запад, похожей на сетку верх-низ-лево-право на карте или на миллиметровке. Вы можете использовать эту сетку, чтобы дать координаты пересечения улицы Фуллертон и Кедзи (отмечено буквой F на карте) по отношению к пересечению Дамен и Норт (S): в двух милях к северу (по Дамен) и в трех милях к западу (по Фуллертон). (Это координаты, а не схема проезда, так что не важно, что они окольные или неточные.)

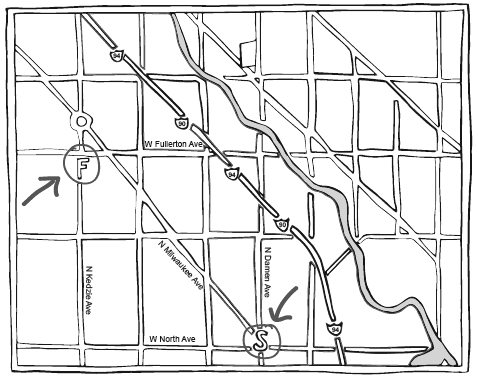
В Чикаго асфальт проложен вдоль трех осей; достаточно любых двух

Север-юг – это одна плоскость, восток-запад – другая. Но два направления, которые вы выберете, не обязательно должны быть перпендикулярны друг другу. Годится любая пара, если только они не указывают в одно и то же направление или в два противоположных. Если вы ограничены только диагональными и западно-восточными дорогами Чикаго, вы все равно сможете подобрать вполне достоверный набор координат: 2¹/₂ миль на северо-запад (по Милуоки) и полмили на запад (по Фуллертон). Или если вы ограничены только диагональными и северо-южными дорогами, вы могли бы сказать: три мили на северо-запад (по Милуоки) и полмили на юг (по Кедзи). Все три системы дают четкое местонахождение F по отношению к S.

Каковы же будут координаты точки в одном дюйме от бетонной стены? Или в футе за ней? У нас может быть самая замечательная линейка в мире, но никакие измерения поверхности стены не приведут нас ни к одной из этих точек. Чтобы справится с этим третьим измерением, нам нужно выбрать третье направление для измерений нашей линейкой: такое, которые выходит из стены. Любое направление подойдет, если оно даст дополнительную информацию, недоступную из двух уже имеющихся. Оно не обязано быть точно перпендикулярным этим двум; оно должно лишь выступать от поверхности стены.

Раз уж на то пошло, мы могли бы добавить и четвертое измерение к координатам, для этого мы бы выбрали четвертое направление, необязательно перпендикулярное остальным трем, но предоставляющее дополнительную информацию. И тут мы сталкиваемся со сложностью. Мы не знаем, как представить направление, которое не является сочетанием длины, ширины и глубины, с которыми мы уже знакомы. У нас нет опыта восприятия этого четвертого независимого направления. Очевидно, что оно не обязательно для выживания, поскольку мы не развили способность его воспринимать. Поэтому не нужно чувствовать себя глупо или опускать руки только потому, что вы не можете представить, как выглядит новое измерение; никто не может.

Иногда помогает представить, как бы вы объяснили, что такое третье измерение, существу, которое только знакомому с двумя. (Иногда. Это. Нужно. Объяснять. Людям. Не переживайте, если вы не относитесь к одному из них.) Например, если бы вы возглавляли строительство дорог для расы человечков – «палка-палка-огуречков», которые живут на поверхности совершенно ровного листа бумаги, вы бы смогли нарисовать огромное количество указателей в одном направлении. Вы бы нарисовали стрелки вверх, вниз и в стороны; вы бы нарисовали длинные стрелки для их автострад и короткие стрелки для дорог, прилегающих к школам; вы бы выбрали двусторонние стрелки для дорог с двусторонним движением и стрелки, заворачивающиеся в кольцо, для кольцевых развязок. Ваши друзья, знакомые только с двумя измерениями, смогли бы увидеть боковые стороны ваших стрелок, но они бы их обошли, потрогали их стороны и углы и поняли бы, куда они указывали.

Но как бы вы нарисовали стрелку, указывающую даже на небольшое расстояние, уходящее с поверхности бумаги? Смогли бы вы использовать законы перспективы, как делают ученые и химики, и нарисовать стрелку, расширяющуюся с одного конца (которые ближе к смотрящему), или кружочек (вид кончика наконечника спереди), или крестик (вид задней части стрелки сзади)? Эти уловки понятны нам, потому что у нас уже есть опыт видения в трех измерениях, но для человечков-огуречков они останутся просто плохо нарисованными стрелками. Они точно не помогут никому из них понять, что такое направление, которое мы называем «выше или ниже листа бумаги».

Это и имел в виду Эдвин Эббот, когда он написал свою «Флатландию» (в 1884 году), очаровательную книгу, которая заставляет задуматься и описывает место, которое Шелдон называет одним из своих любимых для воображаемых посещений . Народ Флатландии, знакомый только с двумя измерениями, живет в своем двухмерном мире, и это похоже на ожившие рисунки на карте. Они не просто довольно-таки плоские, как камбала, например, а они совершенно плоские. У них есть длина и ширина, но у них нет глубины. (Мы знаем много таких людей, на самом деле.) Жители Флатландии имеют форму простых геометрических фигур: квадратов, треугольников и т. д., постоянно смотрящие на стороны, как на портреты друг друга. Они не могут посмотреть друг на друга, стоящими на одной из сторон, но то, что они видят, не кажется им плоским, потому что они не знакомы с понятием толщины. Мистическая сила, которая слегка подтягивает их в южном направлении, дает им ощущение, похожее на силу притяжения.

Флатландцы двигаются, скользя по своему плоскому миру, не осознавая, что существует еще и третье измерение. Их двухмерная вселенная полностью заполняет их восприятие, и они не могут ни нарисовать стрелу, указывающую в каком бы то ни было направлении на поверхности Флатландии, ни отлепиться от нее.

Когда сферическое Нечто, свободно курсирующее по всем трем измерениям, решает пересечь равнину Флатландии, жители воспринимают его как точку, которая неожиданно и необъяснимо появляется, быстро расширяется, превращаясь в круг, а затем снова сжимается в точку перед своим исчезновением. Сфера, летающая неподалеку, видит флатландцев, их очертания и то, что внутри, как рисунки на странице, а они слышат, как она с ними разговаривает. Но как они ни стараются повернуться, они не могут посмотреть на нее, и они ошарашены, когда слышат ее голос «сверху, но при этом не с севера».

Хоть мы и насмехаемся над флатландцами за их невежество, поскольку это дополнительное измерение нам очень понятно, как мы будем выглядеть для гипотетического существа, которое может двигаться в четвертом измерении? И зачем останавливаться на четырех? Есть на самом деле двадцать шесть пространственно-временных измерений, это слишком много направлений, из которых сферическое Нечто сможет смотреть на ваши внутренности, а вы не сможете на него посмотреть в ответ.

Но, возможно, вам не стоит волноваться об этом. Электромагнитное поле, которое переносит свет, скорее всего ограничено уже знакомыми нам измерениями, поэтому никто, кто будет выглядывать из других измерений, не сможет вас увидеть. На самом деле, сила притяжения – это единственное поле, которое может вытекать в другие измерения, а мы так еще и не обнаружили подобные протекания. Так что, если другие измерения и существуют, они скорее всего не простираются очень далеко, а закручиваются, что вполне возможно, потому что пространство может изгибаться.

Если вам сложно представить предмет с бесконечной толщиной, представьте, что Флатландия таки могла простираться в третье измерение. Флатландцы, изображенные Эбботом как живые геометрические фигуры, скользящие по поверхности, вполне могли быть описаны как трехмерные существа, которые воспринимают только части себя (и других), которые находятся в контакте с этой поверхностью.

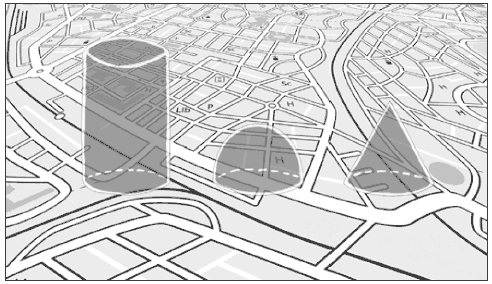
Три «идентичных» флатландских кружочка на прогулке

Цилиндр, полусфера и конус имеют круглый «отпечаток» на флатландской поверхности, поэтому они все могут казаться кругами друг другу и остальным жителям Флатландии, но наблюдатель, способный видеть в третьем измерении, может легко увидеть их различия. Более того, несмотря на их идентичные отпечатки, у них могут быть разные массы – только они не смогут понять причины этого.

Возвращаясь к видению Флатландии как карты, представьте, что вы каким-то образом сможете свести вместе ее восточный и западный края. Флатландец, путешествующий на восток от своего дома, не меняя направления, со временем вернется к западной двери своего собственного дома. Он не почувствует резкий скачок с восточного края карты на западный, поскольку они уже перестанут быть краями; они будут такими же гладкими, как и остальная карта.

Но неужели он не почувствует изгибов бумаги? Не понял бы он – особенно если бы он был так же широк, как и сама карта, – что Флатландия уже не плоская? Нет, если ничего не укажет ему на изогнутость. Он не увидит изгибающийся свет, не почувствует силу, сгибающую его в ту или другую сторону, поскольку свет будет следовать по изгибу бумаги вместе с притяжением и остальными силами. (На самом деле, все наоборот: бумага будет следовать изгибу сил.) И если не было бы никаких экспериментальных возможностей, чтобы различить две вещи (даже в уме), тогда эти вещи останутся идентичными. Как и с суперпозицией состояний, будет так же бесполезно говорить о том, что он ощущает изогнутость пространства, как и говорить, что не ощущает (см. главу 25).

Но есть несколько наблюдений, которые доступны умному флатландцу, чтобы определить, что его мир загнут. Если он может наблюдать два предмета на расстоянии и вычислить размеры огромного треугольника, которые образуют с ним, он может обнаружить, что он не может нарисовать треугольник на плоском листе бумаги, потому что одна из его сторон слишком коротка или длинна, указывая на то, что его пространство загнуто. И если у него хорошее зрение, а Флатландия окажется довольно мала, он может всмотреться и увидеть самого себя (или хотя бы макушку собственной головы) с запада. Или он бы мог посмотреть на запад и увидеть себя с востока. Это не значит, что он увидит другого флатландца, который похож на него как две капли воды, это будет он сам собственной персоной. Если бы он мог видеть еще дальше, он мог бы посмотреть за себя и увидеть еще одного себя на дистанции двух расстояний. И трех. И четырех. Очень подозрительно.

Представим, что северные и южные края карты Флатландии тоже соединили или по отдельности (сформировав шар), или друг с другом (превратив ее в бублик). Теперь наш дальнозоркий флатландец сможет увидеть дополнительные картинки своей головы, глядя на север, юг и во многие другие направления. Если бы его руки были достаточно длинными, он смог бы потянуться и ткнуть сам себя в бок – любого себя, – и одновременно он почувствует тычок. Когда один из него самого переместится, переместятся все остальные, потому что все они – это тот же он.

С его точки зрения, загнутая вселенная совсем не загнутая; это бесконечный плоский лист бумаги, на котором все повторяется до мелочей на определенном расстоянии. Факт, что с вашего «наружного» наблюдательного пункта в третьем измерении вы увидите загибающуюся карту (и свет, и руку), не изменит его собственного восприятия. Он не может «чувствовать» изгиб пространства, но (если он особенно умный флатландец) он может заметить, что этот лес идентичных умных флатландцев создан именно этим. Альтернатива – говорить себе, что пространство не изогнуто и он просто живет в мире из вещей, которые выглядят и ведут себя одинаково, – подпадает под принцип «бритвы Оккама» (см. главу 13).

А разве это не сложный поход к ситуации? Но может ли он каким-то образом аннулировать изогнутость пространства, глядя «мимо», таким же образом, как мы смотрим на восточный горизонт и видим солнце, а не Владивосток? Нет, потому что тогда он будет смотреть в измерении, которое не будет следовать поверхности карты, а мы знаем, что наш флатландец не может этого делать. Каждый луч света, который он видит, приходит к нему вдоль этой поверхности вдоль всех изгибов, и как бы он ни поворачивался, он не сможет отделить свое зрение от него.

Независимо от того, заворачивается ли двухмерный мир вдоль своей поверхности, он может завернуться в третьем измерении. Представьте, что пространство впереди и позади нашей карты Флатландии так плотно завернуто, что оно простирается только на совсем маленькое расстояние, перед тем как завернуться снова. Эффект будет таким же, как будто вокруг бесконечное количество Флатландий, сложенных друг на друга, как стопка карт: в момент, когда вы подниметесь над передней поверхностью Флатландии, вы будете возвращаться в нее с задней стороны. Флатландец, который каким-то образом развил бы способность хоть немного приподнимать свой глаз от поверхности мира, по-прежнему будет смотреть на Флатландию через практически незаметный пробел. Вместо совершенно нового мира, который он надеялся увидеть, он получит все тот же вид.

Ситуация может быть похожей с высшими измерениями, которые Шелдон не изобретал. Принято считать, что во время Большого взрыва все пространственные измерения были одинаково малы; это значит, что их изогнутость была настолько мала, что путешествие вдоль любого из них вернуло бы вас в исходную точку практически сразу же. По непонятным причинам почти четырнадцать миллиардов лет назад некоторые измерения проигнорировали вежливое восклицание в песне Эда Робертсона «Погоди!», и началось быстрое расширение. Но все остальные измерения остались сильно изогнутыми, и мы, словно наш флатландец, смотрящий вверх сквозь бесконечную стопку Флатландий, не получим другого вида, глядя и вдоль любой из них. Когда ученые говорят, что высшие измерения плотно закручены, они не имеют в виду, что они похожи на крошечные спиральки чего-то такого здесь и чего-то другого там. Они говорят, что все, что оставит мир вдоль этих измерений, вернется в него меньше чем через ширину атома.

И почему только некоторые из измерений расширились? Это отличный вопрос, на который нет ответа. Но, когда Шелдон описывает процесс снятия штанов через четвертое измерение (или за него говорил алкоголь), он без сомнения, должен знать, что это невозможно . Не только потому, что мы не знаем, как посылать силу в том направлении, но и потому, что все остальные измерения настолько сильно закручены, что через них невозможно просунуть единственный атом без того, чтобы он не врезался сам в себя, – я уже молчу про пару атомов или пару штанов.

Шелдон: Эль как найтитус эль бозон де Хиггс?

Леонард: В ускорителус частицос .

Большой адронный коллайдер, самый большой ускоритель частиц в мире (или, как сказал Леонард на своем хромающем испанском, «ускорителус частицос»), используется учеными для того, чтобы что есть силы сталкивать атомные ядра друг с другом практически со скоростью света и измерять энергию осколков, которые разлетаются в стороны. Любая энергия, оказывающаяся неучтенной (называемая недостающей поперечной энергией), может быть по причине незамеченных частиц, но также может указывать на энергию, протекающую в другие измерения.

Калтеховский физик-экспериментатор Мария Спиропулу просеивает мусор этих столкновений в поисках доказательств того, что эти новые измерения существуют. Будучи членом проекта Большого адронного коллайдера, который открыл частицу, известную как бозон Хиггса, она еще и является вице-председателем форума Американского физического общества мировой физики.

Спиропулу не понимает презрение Шелдона к физикам-теоретикам, среди которых находится Леонард: «Без экспериментальной физики мы не смогли бы подтвердить существование истинного кварка. Или бозона Хиггса. Но часто мы еще и сталкиваемся с открытиями, которых мы не ожидали и для которых мы не готовили специального оборудования. Космический телескоп Хаббл тому пример: он был создан для получения изображений галактик, а обнаружил доказательства существования темной энергии и искривления Вселенной».

Перед тем как перейти к своему непристойному четырехмерному предложению, Шелдон пытается заставить зрителей подхватить воодушевляющий припев «Песенки про химические элементы» Тома Лерера. На мотив «Песни генерала» из комической оперы Гильберта и Салливана «Пираты Пензаса» положены названия всех 102 известных на тот момент элементов в периодической таблице, и заметьте, в рифму .

За полвека с тех пор, как она была написана, были названы несколько новых элементов. Но последние две строки песни все объясняют:

Лерер писал и исполнял в 50-х и 60-х сатирические песни с отличным умным текстом и идеальными рифмами. Поскольку он получил степень магистра до того, как ему исполнилось двадцать лет, и долгое время проработал учителем математики и музыкального театрального искусства, к нему иногда ошибочно (но вполне объяснимо) обращаются «доктор Лерер».

Вместе с игрой камень-ножницы-бумага-ящерица-Спок (см. главу 23) «Элементы» Лерера стали единственным материалом «Теории Большого взрыва», с которым у Джима Парсонса были проблемы. Парсонс назвал зубрежку песни «без преувеличения самым худшим моментом в моей жизни» .

Вопрос: Джим Парсонс говорит, что теперь «Элементы» врезались ему в память, это как «рана с поля боя – от нее не избавиться» . Вы можете его хоть как-то утешить?

Том Лерер: Возможно, Джим Парсонс просто родился не в то время. Шелдон, живущий всего несколько тысячелетий назад, предпочел бы версию «Элементов» Аристотеля [также написанную Лерером], она немного проще:

Хотя на современном языке их не зарифмуешь. Хотя подозреваю, что на древнегреческом это тоже не получится.