Книга: Решение проблем по методикам спецслужб. 14 мощных инструментов
Назад: Глава 14 Дерево анализа полезности
Дальше: Глава 16 Углубленный анализ полезности
Глава 15
Матрица полезности
Для оценки полезности матрица-таблица заметно удобнее дерева, и тому есть две причины. Во-первых, относительную разницу в степени полезности возможных последствий проще анализировать в формате матрицы. Во-вторых, в таблице проще производить необходимые расчеты. Отчасти дело тут и в том, что эти два инструмента организованы по-разному: дерево оказывается слишком перегружено информацией, оно расползается, иногда оказывается несимметричным, а матрица остается компактной, ясно структурированной, симметричной. Кроме того, в матрице все внимание уделяется исключительно альтернативным вариантам последствий, в то время как в рамках дерева мы вначале представляем все возможные сценарии, а уже потом соответствующие последствия. Работа над сценариями неизбежно отвлекает наше внимание от анализа возможных последствий.
Так чем лучше пользоваться для анализа полезности – матрицей или деревом? Очевидно, что ответ зависит от сути проблемы и предпочтений самого аналитика, работающего над проблемой. Какой бы инструмент мы ни выбрали, основные шаги остаются теми же: нужно построить структуру, то есть матрицу или дерево, записать все варианты сценариев и возможные последствия, решить, с чьей точки зрения будет вестись анализ вариантов, оценить полезности и вероятности, произвести расчет ожидаемых величин и сформировать рейтинг.
С помощью матрицы делать необходимые расчеты проще, поэтому она лучше подходит для работы над проблемами, где требуется посмотреть на ситуацию с разных углов и сравнить возможные последствия разных типов. Я подробно расскажу о подходах к решению подобных задач в следующих двух главах.
А сейчас позвольте мне показать, как использовать матрицу полезности. В табл. 15.1 показаны основные элементы матрицы полезности.
Таблица 15.1. Матрица полезности

В верхнем левом углу мы записываем, с чьей точки зрения ведется анализ. В левой колонке перечисляем все рассматриваемые варианты. Класс рассматриваемых последствий указываем в ячейке над колонками, в названиях которых записываем сами варианты последствий. Для каждой комбинации «вариант – последствия» в матрице должна быть отдельная ячейка, в которой мы записываем полезность и вероятность наступления этой комбинации, а также рассчитанную ожидаемую полезность. Затем суммируем показатели ожидаемой полезности для каждого варианта, результат записываем в колонке «Итого ожидаемая полезность». В последней колонке проставляем позиции в рейтинге.
Сейчас я построю матрицу на основе трех деревьев (рис. 15.1), которые мы делали для упражнения 39, , и вам все станет понятнее. Итоговая матрица приводится в табл. 15.2.
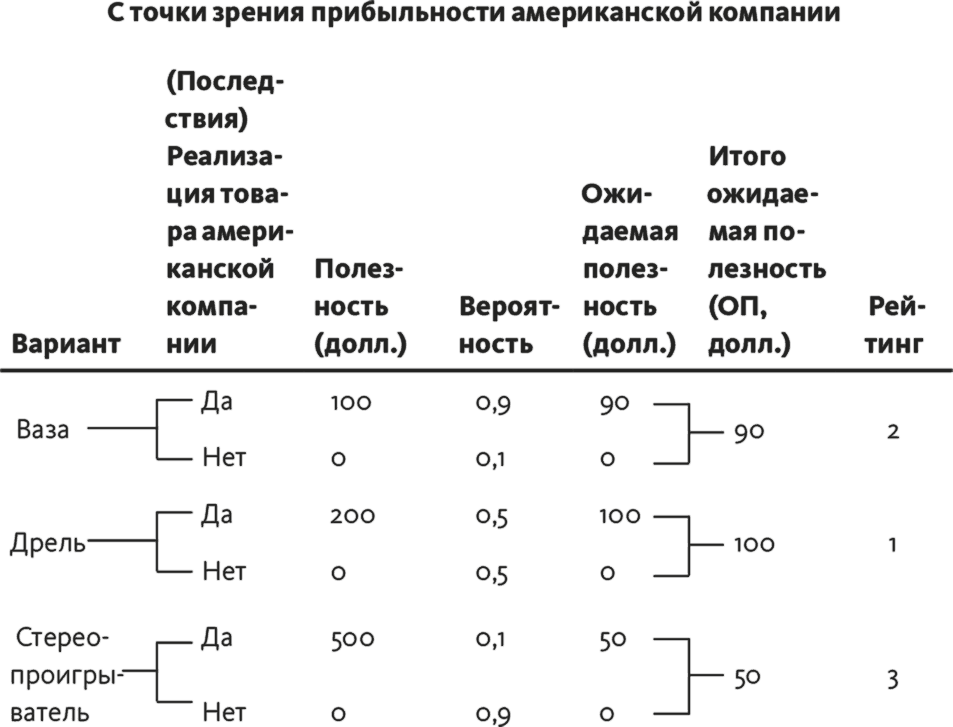
Рис. 15.1
Таблица 15.2

Обратите внимание, как матрица действительно помогает сфокусироваться именно на возможных последствиях: все цифры для каждой комбинации «вариант – последствия» аккуратно заносятся в одну ячейку. Мне лично гораздо проще замечать закономерности, различия и сходства, когда я работаю с матрицей, а не с деревом, – но вообще это вопрос личных предпочтений и привычек, конечно.
Чтобы лучше понять, как работать с матрицей полезности, потренируйтесь и преобразуйте деревья (рис. 15.2), которые мы с вами строили для упражнения из главы 14.
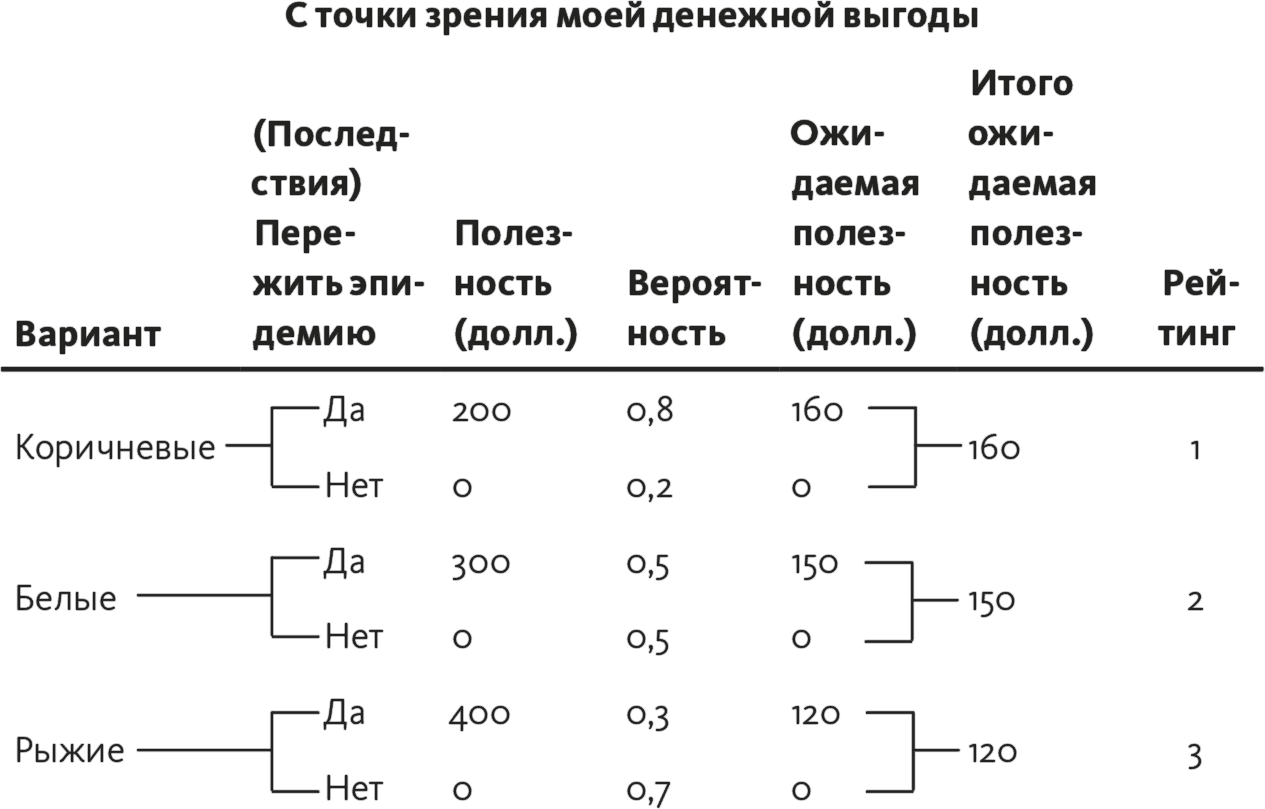
Рис. 15.2

В табл. 15.3 показана матрица полезности для задачи .
Таблица 15.3

Теперь преобразуйте в матрицу деревья полезности из упражнения (рис. 15.3).

Рис. 15.3

В табл. 15.4 показана матрица полезности для задачи .
Таблица 15.4
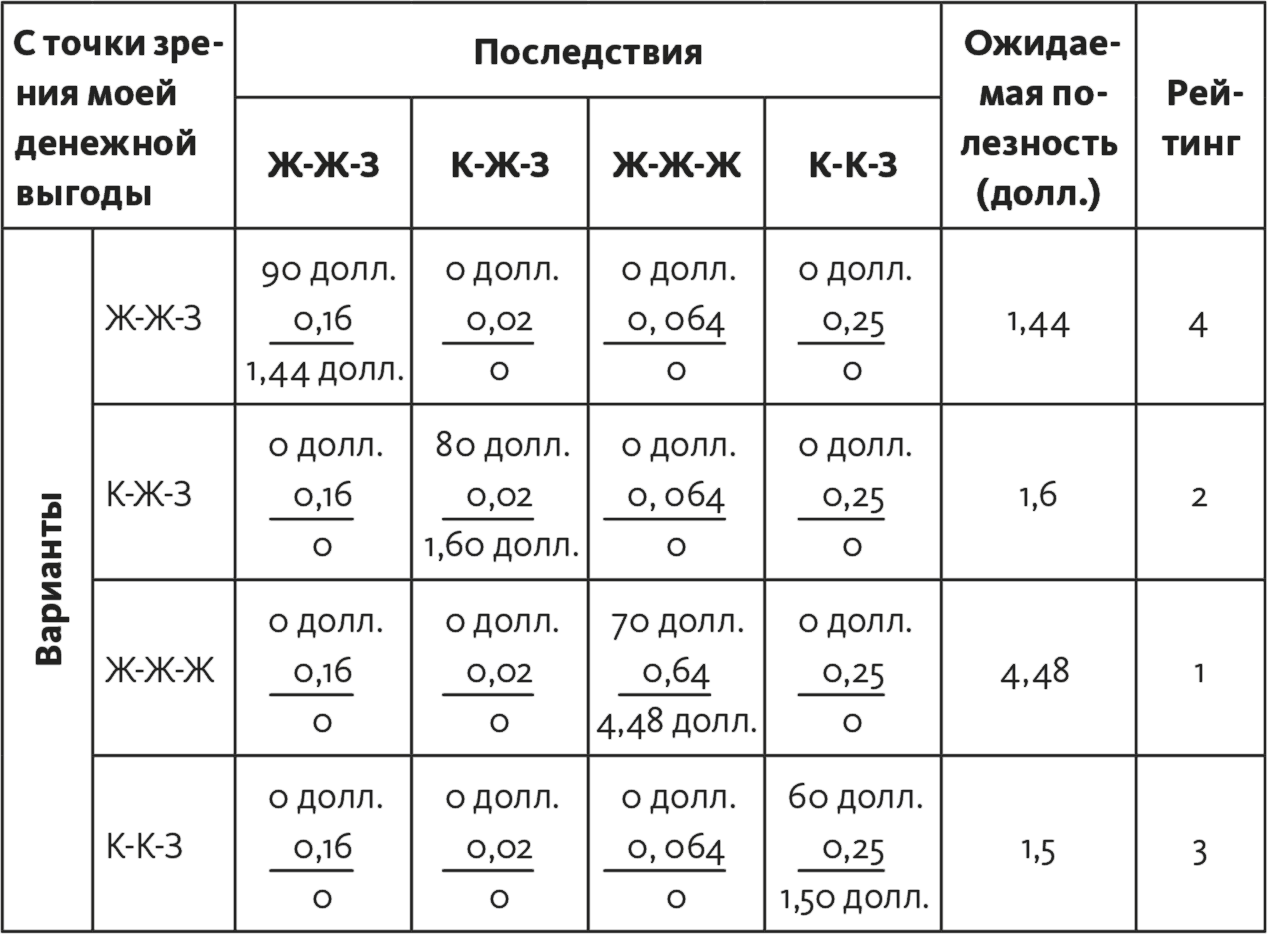
На основе дерева сценариев к задаче постройте матрицу полезности (рис. 15.4).
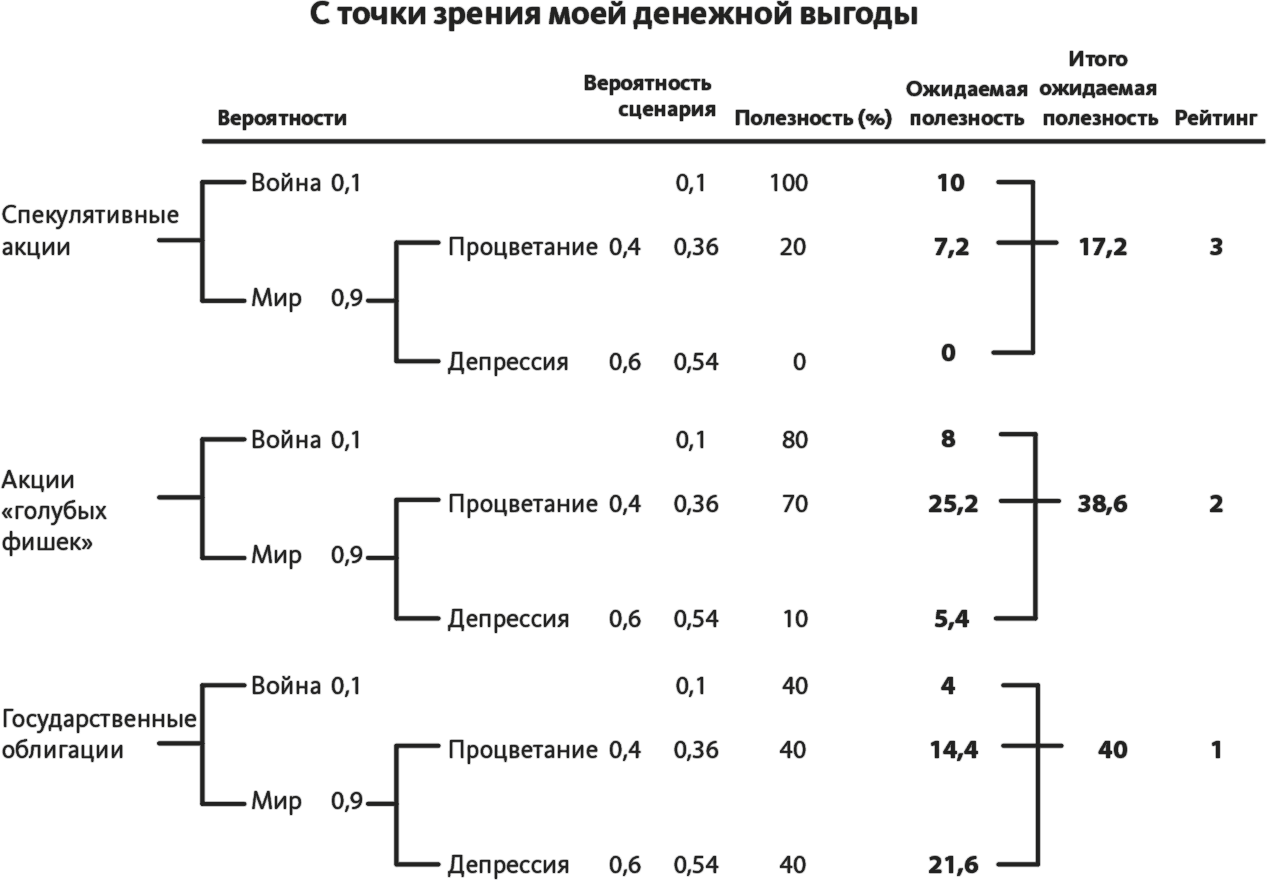
Рис. 15.4

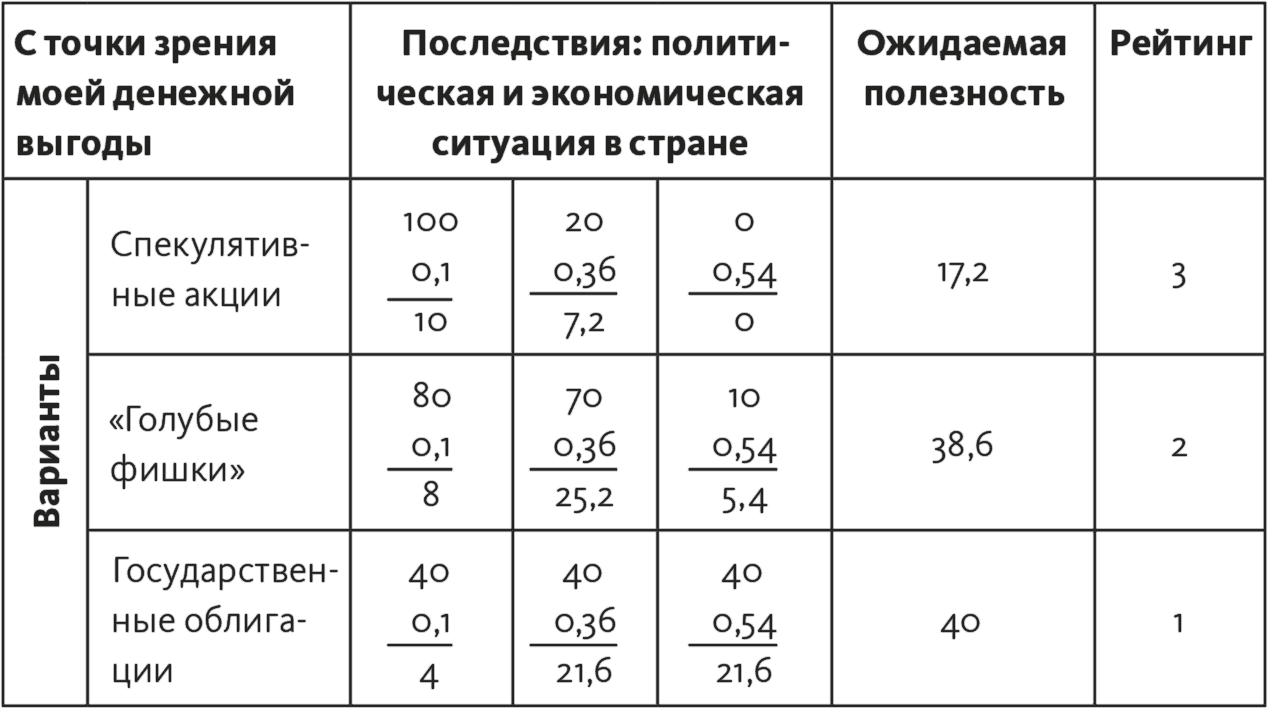
В табл. 15.5 показана матрица полезности для задачи . Типы последствий объединены под общим заголовком «Политическая и экономическая ситуация в стране».
Таблица 15.5
Восемь шагов для анализа матрицы полезности
Шаг 1: очертить круг вариантов и всех возможных последствий, которые нужно проанализировать.
Шаг 2: определить, с чьей точки зрения анализировать ситуацию.
Шаг 3: построить для каждого варианта матрицу полезности
Шаг 4: оценить полезность каждой комбинации «вариант – последствия» для каждого сценария по шкале от 0 до 100 (или использовать полезность в денежном выражении, если есть такие данные). Для этого используется вопрос для оценки полезности: «Если мы выберем этот вариант и наступят ожидаемые последствия, какова будет полезность с точки зрения …?» Хотя бы один вариант должен получить 100 баллов (если не используются цифры в денежном выражении).
Шаг 5: оценить вероятность наступления последствий. Для этого используется вопрос для оценки вероятности: «Если мы выбираем этот вариант, какова вероятность наступления этих последствий?» Сумма вероятностей всех возможных последствий каждого из вариантов должна равняться единице.
Шаг 6: определить ожидаемую полезность, перемножив полезность и вероятность последствий и сложив полученные значения для каждого варианта.
Шаг 7: составить рейтинг вариантов на основе полученных показателей ожидаемой полезности.
Шаг 8: провести проверку результата на здравый смысл.
Проделайте все восемь шагов и проанализируйте задачу (упражнение 15), которую мы обсуждали в главе 8. Вот еще раз условия задачи.
Упражнение 43. Прогноз погоды, дилемма II
Представим, что вы объявляете прогноз погоды на местном телеканале. Вероятность того, что завтра, в рабочий день, пойдет снег, составляет 1 %. С помощью матрицы полезности определите, что выгоднее с точки зрения ваших интересов: объявить, что завтра пойдет снег, или сообщить, что снега не будет. Рассматривайте только два варианта: снег пойдет, или снег не пойдет.

предложены в конце книги.
Я лично присвоил комбинации «объявить, что пойдет снег, – снег пошел» 100 баллов полезности, потому что большинство людей работают, а значит, хотя они и ненавидят снегопады, из-за которых замедляется движение и срываются планы, но все же предпочтут знать о его приближении заранее. Поэтому я считаю, что это лучший вариант в нашей матрице с точки зрения того, кто объявляет погоду в новостях: такое поведение укрепит доверие аудитории и поможет зрителям подготовиться к возможному снегопаду, за что они будут признательны.
Худшим я считаю вариант «объявить, что снега не будет, – снег пошел», его полезность я оцениваю на 0 баллов. И правда, что может быть хуже в контексте интересов синоптика, объявляющего прогноз погоды?
Варианту «объявить, что снег пойдет, – снег не пошел» я присвоил 80 баллов: все-таки люди готовы к снегопаду и рады, что его не было. Это может отчасти компенсировать падение доверия к человеку, объявляющему погоду, хотя в этом случае у него может сложиться репутация паникера.
Вариант «объявить, что снега не будет, – снег не пошел» получает 30 баллов: хотя люди и рады, что снегопада не случилось, это просто ненаступление условий.
Вероятности нам были даны: вероятность снегопада 0,1, тогда вероятность того, что снег не пойдет, 0,9.
Я умножаю вероятность на полезность и получаю ожидаемую полезность. Сложив величины ожидаемой полезности, получаю итоговую ожидаемую полезность и могу сформировать рейтинг. По моей оценке, вариант «объявить о снегопаде» – наиболее предпочтительный. (Кстати, сейчас становится понятнее, почему в прогнозах погоды на телевидении и радио нам так часто объявляют о возможном снегопаде, как только появляется малейшая вероятность: они боятся оказаться в нижней левой ячейке подобной матрицы.)
Предложите эту задачу приятелям на вечеринке: гарантирую, что обсуждение полезности каждой из ячеек будет крайне живым и увлекательным.
И последнее упражнение в этой главе: тут вам придется немного поразмышлять о том, как лучше провести анализ полезности. Пожалуйста, вначале решите задачу с помощью дерева полезности, а потом постройте и матрицу и проведите оценку еще раз.
Упражнение 44. Захват самолета (2)
Группа террористов захватила самолет и требует освободить их товарищей, находящихся в тюрьме в другой стране. Вы командуете группой по борьбе с террористами и получили приказ определить, стоит ли предпринять попытку вооруженного захвата самолета с целью освобождения пассажиров и экипажа.
Вы тщательно проанализировали ситуацию и пришли к выводу, что в случае попытки освобождения заложников вероятность того, что и пассажиры, и члены экипажа погибнут, составляет 0,1; вероятность того, что будут убиты лишь некоторые, составляет 0,8; вероятность того, что никто из заложников не будет убит, составляет 0,1. Если все заложники будут убиты, то вероятность освобождения арестованных террористов составляет 0; если кто-то из заложников останется в живых или вообще никто из них не погибнет, вероятность освобождения арестованных террористов составляет 0,1. Вы также определили, что, если не предпринимать попытки освободить заложников, вероятность, что арестованные террористы будут освобождены, составляет 0,9.
Часть 1: с помощью восьми шагов анализа на основе дерева полезности определите, стоит ли предпринимать попытку освобождения заложников (полезность каждого из возможных последствий оцените сами).
Часть 2: на основе деревьев полезности постройте единую матрицу полезности.

В я предлагаю собственную версию дерева полезности. В показана моя версия матрицы. В результате анализа я прихожу к выводу, что стоит предпринять попытку освободить заложников, так как совокупная ожидаемая полезность этого варианта почти вдвое превосходит полезность варианта, при котором попытки освободить заложников не предпринимается.

