Для начала введем обозначения. Пусть р – заданное простое число, g – заданное натуральное число, g < p. На самом деле g это так называемый первообразный корень числа р. Об этом мы расскажем ниже, в и к главе 6. Цель данного раздела – доказать, что в схеме Диффи – Хеллмана Алиса и Боб действительно получают один и тот же ключ.

Для любых натуральных чисел n и р мы воспользуемся стандартным обозначением для остатка от деления n на р:

n(mod p) = [остаток от деления n на p].

(Читается «n по модулю p».)

Итак, Алиса задумала число х, а Боб число у. Схема Диффи – Хеллмана состоит из двух шагов.

Шаг 1. Алиса передает Бобу

a = (g^x) (mod p).

Боб передает Алисе

b = (g^y) (mod p).

Шаг 2. Алиса вычисляет ключ

K_A = (b^x) (mod p).

Боб вычисляет ключ

K_B = (a^y) (mod p).

Утверждение. Боб и Алиса получили один и тот же ключ K = K_A = K_B.

Доказательство. Нам нужно доказать, что K_A = K_B. Поскольку а и b – это остатки от деления на р, то существуют такие целые числа k и l, при которых

a = g^x − kp, b = g^y − lp.

Подставив эти выражения в формулы для ключей, получаем:

K_A = (g^y − lp)^x (mod p),

K_B = (g^x − kp)^y (mod p).

Заметим, что в выражении для K_A можно расписать (g^y − lp)^x следующим образом:

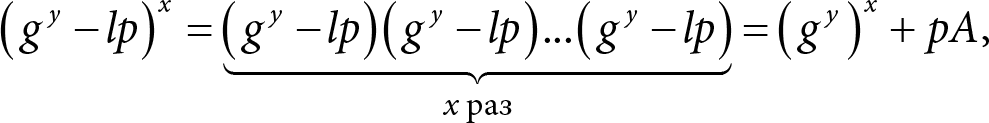
где А – это целое число, то есть рА делится на р. Таким образом получаем

K_A = ((g^y − lp)^x) (mod p) = ((g^y)^x + pA) (mod p) = (g^y)^x (mod p).

Совершенно аналогично для какого-то целого числа B получаем

K_B = ((g^x − kp)^y) (mod p) = ((g^x)^y + pB) (mod p) = (g^x)^y (mod p).

Результат теперь очевиден, поскольку

(g^y)^x = g^yx = g^xy = (g^x)^y.

Вспомним, что логарифм числа у по основанию g – это такое число х, для которого выполняется

g^x = y.

Легко заметить, что очень похожая операция лежит в основе схемы Диффи – Хеллмана.

После возведения в степень мы берем остаток от деления на р. Как мы уже упоминали выше, в математике такая операция обозначается g^x (mod p) (читается «g в степени х по модулю р»). При этом, естественно, g и х натуральные числа и у g нет общих делителей с р.

Одна нетривиальная теорема из теории чисел (см., например,) утверждает, что для каждого простого р существует такое число g, что все числа

разные, то есть служат перестановкой множества 1, 2, …, p − 1 (среди них нет нуля, поскольку g < p и, значит, g^х не делится на р). Например,

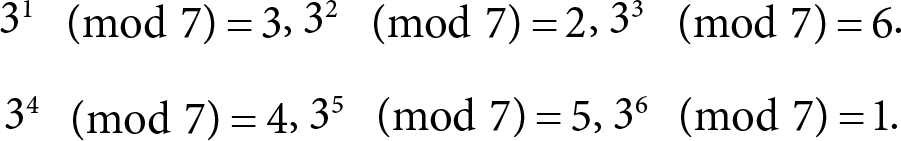
Из этого следует возможность корректного определения дискретного логарифма, который еще называется индексом. А именно: «логарифм» произвольного числа y ∈ {1, 2, …, p − 1} по основанию g – это тот самый, уникальный, x ∈ {1, 2, …, p − 1}, при котором выполняется g^x (mod p) = y. Поскольку для всех x < p остатки разные, то х определяется однозначно. Операция нахождения такого х называется операцией дискретного логарифмирования. Она очень сложная, и никто не знает, можно ли придумать способ ее быстрой реализации.

Как определить такое число g, чтобы все остатки в выражении (П.15) были разные? Число g обладает этим свойством, если оно является первообразным корнем числа р. Мы позволим себе рассказать об этом понятии немножко подробнее.

Есть такая теорема Эйлера: если х и m взаимно просты, то g^φ(m) ≡ 1. Здесь a ≡ b, если a − b делится на m. Другими словами, у а и b одинаковый остаток от деления на m. А φ(m) это функция Эйлера, равная количеству чисел, не превосходящих m и взаимно простых с ним. Например, если m = p, где р простое, то φ(p) = p − 1 и теорема Эйлера превращается в малую теорему Ферма.

Условие теоремы Эйлера достаточное, но не необходимое. Вполне может случиться и так, что x^a ≡ 1 (mod m), хотя a < φ(m). Самый простой пример такой ситуации – это, конечно, x = 1. Действительно, x^a ≡ 1 (mod m) для любых натуральных a и m. Но есть и менее тривиальные примеры. Скажем, p = 5, а 4² = 16 ≡ 1(mod 5), хотя 2 < p − 1 = 4.

Формально число g называется первообразным корнем по модулю m, если

Пример (отсутствие первообразных корней у m = 2^k). Возьмем m = 2^k при k ≥ 3. В этом случае можно показать, что для любого натурального х выполняется

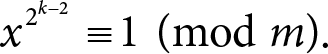
При этом φ(m) = 2^k−1, потому что числа, взаимно простые со степенью двойки, – это все нечетные числа, а их ровно 2^k−1. Значит, для любого х нашлось число

a = 2^k−2 < 2^k−1 = φ(m),

для которого выполняется x^a ≡ 1 (mod m). Получается, что у m = 2^k при k ≥ 3 первообразных корней нет.

Теперь мы можем объяснить, почему в качестве m удобно брать простое число р. Для простого р всегда существуют первообразные корни. На самом деле мы уже говорили о них выше, в , только не называли этим термином. Это те самые числа g, которые дают разные остатки от деления на p в (П.15). Например, при p = 3 это g = 2, при p = 5 это g = 2, а при p = 7 это g = 3. В нашем примере в тексте главы число g = 2 – это один из первообразных корней числа p = 19.

Итак, если g – первообразный корень p, то все остатки в (П.15) разные и каждому остатку соответствует единственная степень х (дискретный логарифм, он же индекс), при которой такой остаток получается. Ничего подобного мы не можем сделать, если будем брать остаток от деления на число m, для которого первообразного корня нет. Именно поэтому работают с простыми числами.

Заметим, что первообразные корни есть еще для m = 4, m = p^k и m = 2p^k. Но все равно с простыми числами работать проще.