Книга: Кому нужна математика? Понятная книга о том, как устроен цифровой мир
Назад: HyperLogLog-счетчики
Дальше: Глава 8 Миллион аукционов в минуту
Четыре виртуальных рукопожатия
Помимо того что задача подсчета важна сама по себе, она находит и другие, совершенно неожиданные применения.
Все мы знаем, что мир тесен. Знакомишься с человеком, и тут же находятся общие знакомые или хотя бы знакомые знакомых. Многих исследователей интересовал вопрос, насколько тесен виртуальный мир социальных сетей.
Вопросы подобного рода имеют длинную историю. В конце 1960-х годов социолог Стэнли Милграм провел свой знаменитый эксперимент. Он раздал случайным людям в штатах Небраска и Канзас письма, адресованные брокеру из Бостона. Географически и по роду занятий эти люди были достаточно далеки от адресата. По правилам эксперимента, участники могли переслать письма только своим знакомым, которые должны были передать их дальше, своим знакомым, и так далее, пока они в конце концов не достигнут адресата. Из 296 писем большинство затерялось в дороге, но 64 письма дошли-таки по назначению. При этом оказалось, что цепочка, связывающая совершенно незнакомых людей, на удивление короткая. В среднем отправителя и адресата разделяло всего 5 человек! На рис. 7.1 мы схематически изобразили, как письмо пересылалось всего шесть раз, через пять промежуточных человек.

Рис. 7.1. Схематическое изображение эксперимента Стэнли Милграма. Участники могли переслать письмо только своим знакомым. Письмо от отправителя до адресата пересылалось 6 раз, через 5 разных человек
Так родилось понятие «шести рукопожатий». Если вы пожмете руку всем своим знакомым, ваши знакомые пожмут руку своим знакомым и так далее, то понадобится всего шесть рукопожатий, чтобы соединить вас с любым человеком на Земле!
Эксперимент Милграма не идеален, неслучайно столько писем затерялось в дороге. Но в то время просто не было другого способа выяснить, кто, с кем и через кого знаком. Зато сейчас таких данных сколько угодно.
Чтобы провести подобный эксперимент в «Фейсбуке», не нужно даже беспокоить участников. На сервере сети хранится полная информация, кто с кем дружит. Остается только вычислить количество «виртуальных рукопожатий», отделяющих одного пользователя от другого. Можем ли мы это сделать? Именно такой вопрос задали научные сотрудники «Фейсбука» профессору Миланского университета Себастьяно Винье.
И Себастьяно, и сотрудники социальной сети понимали, что это колоссальная задача. Неслучайно она не была решена раньше. У «Фейсбука» свыше 700 миллионов активных пользователей, то есть более
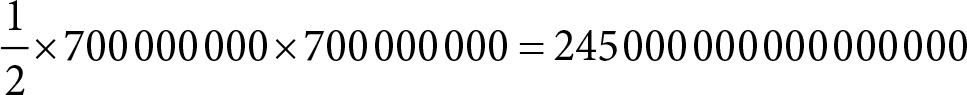
пар пользователей. И нужно вычислить длину цепочки для каждой пары! Но дело не только в этом. Ключевая проблема – опять же в количестве оперативной памяти, и возникает она потому, что между двумя пользователями не одна, а несколько цепочек разной длины. Для примера посмотрим на маленькую социальную сеть на рис. 7.2. А отделяет от В одно рукопожатие или два – через Г. Разных цепочек очень много, потому что друзья друзей зачастую наши друзья. В социальных сетях это известный, проверенный и доказанный феномен. При этом нас интересует самая короткая цепочка.
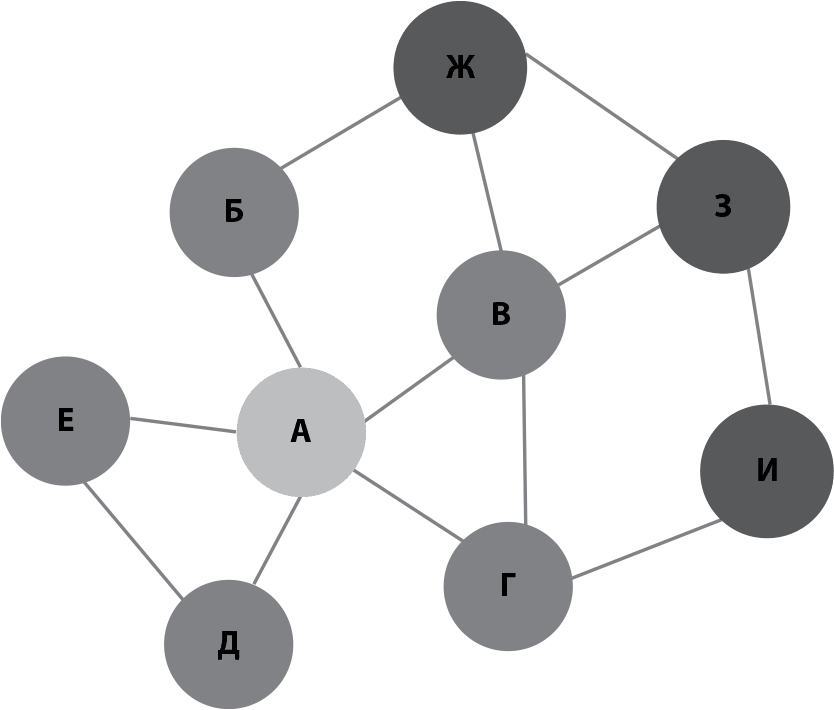
Рис. 7.2. Социальная мини-сеть. Кружками с буквами обозначены пользователи, линия между двумя пользователями означает, что они друзья. Мы обозначили пользователя А светло-серым цветом, а его друзей – серым. Темно-серым цветом обозначены пользователи, которых от А отделяют два рукопожатия
Компьютеру совсем нетрудно считать с диска всех «друзей друзей» пользователя А. Но только некоторых из них отделяет от А одно рукопожатие, а некоторых – два. Например, на рис. 7.2 и В, и Ж – это друзья друзей А. Но В друг А, а Ж – нет. Как определить, что Ж на расстоянии двух рукопожатий? Только одним способом – запомнить всех друзей А. Именно так работает самый распространенный метод под названием поиск в ширину.
Если теперь добавить всех «друзей друзей друзей», а потом их друзей и так далее, то нужно запоминать всех, кого мы видели на расстоянии один, два, три… После пяти-шести шагов мы уже видели практически всех пользователей сети. Держать в оперативной памяти 700 миллионов имен, или разных чисел, – ну просто абсолютно нереально!
Сотрудники «Фейсбука» поверили в успех, потому что Себастьяно Винья и его коллеги придумали абсолютно иной способ подсчета числа рукопожатий. Они заметили, что самая главная проблема – необходимость запоминать увиденных пользователей – совершенно аналогична задаче о подсчете. А последнюю можно решить методом HyperLogLog.
Для интересующихся читателей ниже во врезках мы объясняем основные идеи с помощью примера на рис. 7.2. Этот текст не требует математической подготовки, но, если вы не хотите вдаваться в подробности, можете его пропустить.
Применение HyperLogLog-счетчика для подсчета числа рукопожатийХорошая новость: можно очень легко вычислить всех друзей любого пользователя.Присваиваем хеш-значение каждому пользователю. Запускаем счетчик HyperLogLog и просматриваем пользователей начиная с А. На каждом шаге HyperLogLog будет сообщать, сколько всего разных пользователей мы видели. Оказывается, это все, что нам нужно.Начнем с пользователя А. Это один пользователь, на расстоянии ноль рукопожатий от самого себя. Теперь посмотрим на его друзей:Б В Г Д Е,HyperLogLog сообщит нам, что всего с момента запуска мы видели 6 пользователей. Минус А, получаем 5 пользователей на расстоянии одного рукопожатия. Теперь к А и его друзьям добавляем всех тех, кто дружит с друзьями А:друзья Б: А, Ж,друзья В: А, Г, Ж, Здрузья Г: А, В, Идрузья Д: А, Едрузья Е: А, Д.После этого HyperLogLog сообщит, что всего с момента запуска мы видели 9 разных пользователей. Вычитаем А и число его друзей, получается9 − 1 − 5 = 3пользователя на расстоянии двух рукопожатий от А. Заметьте, что нам не нужно запоминать самих друзей А, а только их количество!В данном случае больше пользователей у нас нет. В реальности процесс продолжается. На третьем шаге мы добавляем всех «друзей друзей друзей». После этого HyperLogLog опять сообщает, сколько разных пользователей мы видели до сих пор. Вычитаем из этого числа количество пользователей на расстоянии ноль, один и два и получаем число пользователей, которых от А отделяют ровно три рукопожатия. И так далее.Процесс будет завершен, когда мы увидим всех пользователей сети. Как вы помните, HyperLogLog держит в памяти лишь максимальное число нулей в хеш-значении. В дополнение к этому надо запомнить только число пользователей на расстоянии одного, двух, трех и так далее рукопожатий. Это тоже занимает очень скромный объем оперативной памяти.
HyperLogLog требует так мало памяти, что процесс можно запустить для всех пользователей одновременно и в результате получить общее число пар на расстоянии одного, двух, трех рукопожатий и так далее. Конечно, результаты приблизительные, но их точность очень высокая.
Оказалось, что двух пользователей «Фейсбука» в среднем разделяет не шесть, а всего 4,74 рукопожатия! Статья Себастьяно Виньи и соавторов быстро обрела известность в научном мире и за его пределами. О ней писали ВВС и New York Times. Результаты уже сейчас попали в популярную литературу и специальные учебники. Виртуальный мир оказался еще теснее, чем реальный – тот, в котором мы живем!
Филипп Флажоле
Филипп Флажоле умер в 2011 году, когда работа над внедрением HyperLogLog была в самом разгаре. Блог под названием «HyperLogLog – краеугольный камень инфраструктуры больших данных» был написан в 2012 году. Статья о 4,74 виртуальных рукопожатий в «Фейсбуке» вышла в том же 2012 году, а статья сотрудников Google – в 2013-м. Система Redis внедрила HyperLogLog в 2014 году. В честь Филиппа Флажоле команды HyperLogLog начинаются с его инициалов PF.Нам неизвестно, успел ли Флажоле узнать, что его результаты уже стояли на пороге широкого внедрения. Мы закончим последними фразами из блога, где автор подробно и с большим энтузиазмом объясняет HyperLogLog широкой технической публике:…Мне очень жаль, что я не был знаком с ним лично. Я уверен, что его труды будут жить дальше, но наука и индустрия, безусловно, потеряли выдающийся интеллект. Продолжай считать, Филипп, мы на тебя рассчитываем!
Назад: HyperLogLog-счетчики
Дальше: Глава 8 Миллион аукционов в минуту

