Математики уже давно договорились, что такое шар. Шар состоит из всех точек, которые удалены от центра не больше чем на какое-то заданное расстояние, обозначаемое буквой r, – радиус. В нашем привычном трехмерном пространстве, где расстояния измеряются в метрах, это обычный шар, как на рис. 3.1.

Рис. 3.1. Шар радиуса r в трехмерном пространстве. Все точки удалены от центра не больше чем на расстояние r

Зато понятия точка и расстояние в математике абсолютно абстрактные. Есть несколько простых правил, которых следует строго придерживаться, но в рамках этих правил – полная свобода. Точками могут быть сигналы, а могут – кривые и даже результаты случайных экспериментов. И расстояния между ними можно определить самыми разными способами. В итоге получаются «шары», не поддающиеся воображению. Тем не менее эти абстрактные шары играют в математике очень большую роль.

В теории кодирования точка – это кодовое слово, то есть последовательность нулей и единиц заданной длины. А расстоянием принято считать так называемое расстояние Хэмминга.

Расстояние Хэмминга между двумя кодовыми словами – это всего-навсего число позиций, на которых у этих слов стоят разные символы: у одного 0, а у другого 1. Например, на рис. 3.2 расстояние Хэмминга между двумя кодовыми словами равно трем. Мы заключили в рамки те позиции, где эти два кодовых слова отличаются друг от друга.

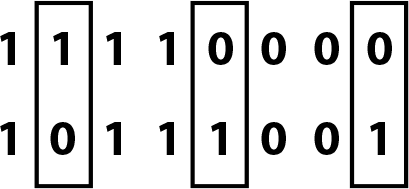
Рис. 3.2. Расстояние Хэмминга между двумя кодовыми словами – число позиций, на которых у этих слов стоят разные символы. На рисунке это расстояние равно трем. Позиции, где два кодовых слова отличаются друг от друга, заключены в рамки

Что происходит, если при передаче, скажем, слова 111000 произошла одна ошибка?

Получится другое слово, которое будет отличаться от 111000 всего на одной позиции. Иначе говоря, если у нас при передаче происходит не больше одной ошибки, расстояние Хэмминга между отправленным и полученным кодовым словом будет не больше единицы. Давайте снова посмотрим на перечень (3.1) предыдущего раздела:

Расстояние Хэмминга между словом 111000 и любым другим словом из перечня не превосходит 1. Значит, этот список – не что иное, как шар радиуса 1 с центром 111000!

Кстати, подобное определение можно ввести и для обычных слов русского языка одинаковой длины. Например, расстояние Хэмминга между словами «дочка» и «точка» равно единице, а между словами «точка» и «галка» – трем. Если слово «точка» – это центр шара Хэмминга радиуса 1, то слово «дочка» входит в этот шар, а слово «галка» – нет.

Шары Хэмминга очень трудно себе представить даже для маленьких кодов. На рис. 3.3 мы изобразили расстояния Хэмминга между кодовыми словами длины 3. Расстояния Хэмминга могут быть 0, 1, 2 или 3. На рисунке чем темнее цвет, тем больше расстояние. Если взять, например, колонку 000, то шар Хэмминга радиуса 1 – это все белые и светло-серые квадратики в этой колонке: 000, 001, 010, 100. Сразу видно, что расположение белых и, скажем, самых темных квадратиков в колонках неодинаковое, хотя, конечно, в рисунке много закономерностей. Например, рисунок из самых светлых тонов (белый и светло-серый) абсолютно симметричен рисунку из двух оставшихся более темных тонов.

Рис. 3.3. Расстояние Хэмминга между кодовыми словами длины 3. Справа изображен цветовой код. Расстояния: 0, 1, 2, 3. Чем темнее цвет, тем больше расстояние

Кодовые слова длины 3 – очень простой пример, их всего восемь. Стоит чуть увеличить длину кодового слова, и из-за уже знакомого нам экспоненциального закона слов станет так много, что картинка нам не поможет. Профессор Джон Слэни из Австралийского национального университета сделал замечательный рисунок, на котором изображены расстояния Хэмминга между кодовыми словами длины 8, а это всего один байт. Таких слов 256. Советуем заглянуть на веб-страницу Слэни и посмотреть на этот рисунок. Вам сразу станет понятно, что он никак не поможет найти хороший код. Картинка скорее напоминает красивый коврик. Нам нужен другой математический аппарат, и, к счастью, такой аппарат есть. Теория кодирования тесно связана с комбинаторикой – наукой о комбинациях тех или иных объектов.

Возможно, вы уже заметили связь между шарами Хэмминга и кодами, исправляющими ошибки. Допустим, мы передаем кодовые слова длины 10 и хотим, чтобы код исправлял две ошибки. Тогда надо построить код, в котором шары с центрами в кодовых словах и радиусами 2 попарно не пересекались бы. Все последовательности нулей и единиц в таком шаре будут означать одно и то же кодовое слово. Иначе говоря, кодовые слова должны отличаться друг от друга настолько, чтобы при наличии двух ошибок их невозможно было перепутать. На языке математики это значит, что расстояния Хэмминга между кодовыми словами должны быть как минимум равны 5.

При создании кодов возникает немало интересных вопросов. Например, очень важно, чтобы количество кодовых слов было как можно большим, так как это позволит передать по каналу связи больше информации, исправляя при этом заданное наперед количество ошибок (характерное для данного канала связи). Отыскание максимальных кодов при заданной длине кодового слова и количестве ошибок – крайне трудная и не до конца решенная математическая задача. По сути, это задача комбинаторики, хотя и мотивированная совершенно практическими вопросами кодирования информации.