Теорема Пифагора является, пожалуй, чуть ли не самой популярной теоремой в геометрии. И уж точно одной из самой популярных в математике вообще. Поэтому в том, что ей посвящен целый раздел нашей «геометрической» главы, нет ничего странного.

Итак, в прямоугольном треугольнике сторона, лежащая напротив угла в 90°, называется гипотенузой, другие две стороны – катетами. В треугольнике, изображенном чуть ниже, катетами являются отрезки BC (длиной a) и AC (длиной b), а гипотенузой – отрезок AB (длиной c).

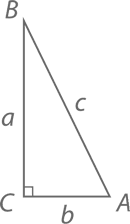
Теорема Пифагора: В прямоугольном треугольнике с катетами длиной a и b и гипотенузой длиной c

Существует более трех сотен различных доказательств этой теоремы, но мы остановимся лишь на самых простых. Можете пропускать некоторые из них, если хотите: моя основная цель заключается в том, чтобы хотя бы одно из них заставило вас улыбнуться, а может быть, даже восхититься.

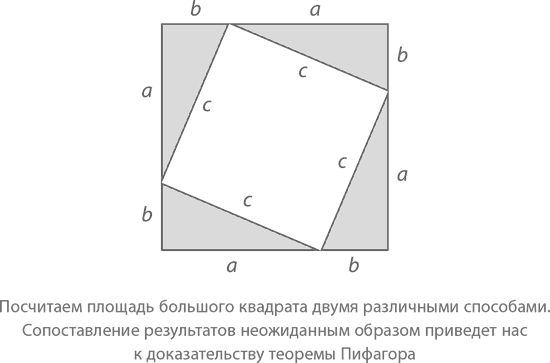
Доказательство 1: Ниже на рисунке изображен квадрат, составленный из четырех конгруэнтных прямоугольных треугольников.

Вопрос: Какова площадь этого квадрата?

Ответ 1: Длина каждой из сторон квадрата равна a + b, следовательно, его площадь составит (a + b)² = a² + 2ab + b².

Ответ 2: С другой стороны, большой квадрат состоит из четырех треугольников, площадь каждого из которых равна ab/2, и пустого (тоже квадратного) пространства между ними, площадь которого равна c². (Кстати, откуда мы взяли, что оно является квадратным? Во-первых, мы знаем, что его стороны равны. Во-вторых, благодаря правилу симметрии, мы можем убедиться в том, что равны и все его углы: если повернуть эту фигуру на 90°, она будет абсолютно идентична изначальной, а значит, все ее углы должны быть одинаковыми. Так как сумма углов любого четырехугольника всегда составляет 360°, мы можем сделать вывод, что каждый из четырех углов нашей фигуры равен 90°.) Следовательно, их общая площадь выглядит как 4(ab)/2 + c² = 2ab + c².

Сведем первый и второй ответы к одному уравнению:

Вычтем 2ab из обеих сторон и получим

что и требовалось доказать.☺

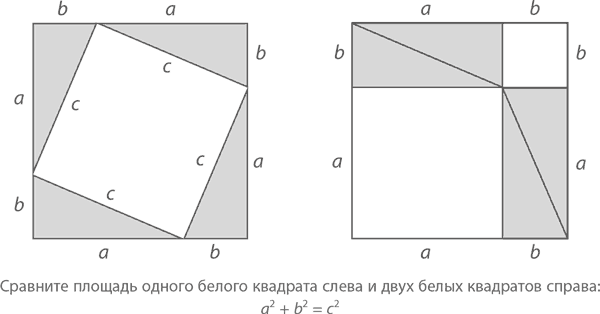
Доказательство 2: Возьмем ту же фигуру, что и в предыдущем доказательстве, только немного поменяем расположение треугольников в ней. И если на левом рисунке очевидно, что площадь пустого пространства равна c², то на правом она уже составит a² + b². Следовательно, c² = a² + b², что и требовалось доказать.☺

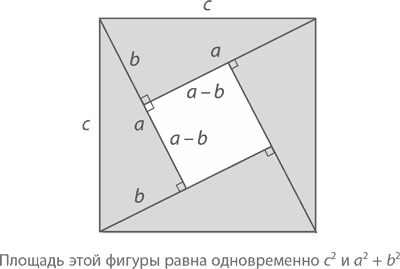
Доказательство 3: Снова передвинем треугольники, только на этот раз так, чтобы они располагались более компактно (как на следующем рисунке), а c² была бы площадью не маленького внутреннего, а большого квадрата (это будет все еще квадрат, ведь каждый его угол есть сумма ∠A и ∠B, то есть 90°). Общая площадь треугольников по-прежнему равна 4(ab/2) = 2ab. Площадь же внутреннего пустого пространства составит (a – b)² = a² – 2ab + b². Соединив все вместе, имеем 2ab + (a² – 2ab + b²) = a² + b², что и требовалось доказать.

Доказательство 4: Это будет доказательство подобием, поэтому нам нужно сначала вспомнить все, что мы знаем и подобных треугольниках. В прямоугольном треугольнике ABC проведем линию CD так, чтобы она была перпендикулярна гипотенузе AB, как на рисунке:

Обратите внимание, что треугольник ADC содержит как прямой угол, так и ∠A, из чего следует, что его третий угол должен быть конгруэнтным ∠B. Подобным же образом треугольник CDB содержит как прямой угол, так и ∠B, из чего следует, что его третий угол должен быть конгруэнтным ∠A. Следовательно, все три треугольника будут подобными:

Имейте в виду, что порядок букв здесь имеет важное значение: ∠ACB = ∠ADC = ∠CDB = 90° являются прямыми углами, как и ∠A = ∠BAC = ∠CAD = ∠BCD и ∠B = ∠CBA = ∠DCA = ∠DBC. Сопоставление длин сторон первых двух треугольников дает

Точно так же для первого и третьего треугольников –

Сложим эти два уравнения и получим

А так как AD + DB = AB = c, мы приходим к

что и требовалось доказать.☺

Следующее доказательство будет чисто геометрическим – никакой алгебры, зато очень много непростой визуализации.

Доказательство 5: В этот раз возьмем два квадрата с площадями a² и b². Расположим их вплотную друг к другу – как показано на рисунке слева, и их общая площадь тогда составит a² + b². «Разрежем» получившуюся фигуру на два прямоугольных треугольника (длины катетов составят a и b, длина гипотенузы – c) и один странной формы геометрический объект. Обратите внимание, что угол в нижней части этого «странного объекта» должен быть равен 90°, потому что его окружают ∠A и ∠B. Представьте себе, что в левом верхнем углу большого квадрата и правом верхнем углу маленького квадрата расположено нечто вроде опорных стержней, вокруг которых потенциально может происходить «вращение» (подобно тому, как комнатная дверь «вращается» вокруг дверной петли, закрепленной на косяке).

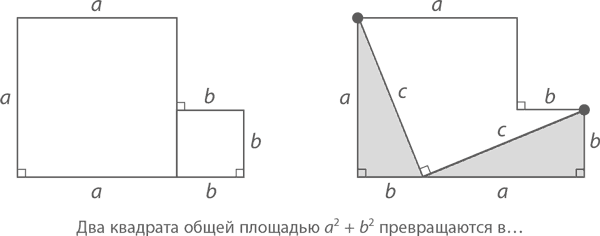
А теперь мысленно поверните нижнюю часть левого треугольника на 90° против часовой стрелки – так, чтобы «вывести» его за верхнюю границу большого квадрата. Поверните на 90° и второй треугольник, только теперь по часовой стрелке – так, чтобы прямые углы «легли» один на другой в точке сочленения двух квадратов, как показано на рисунке:

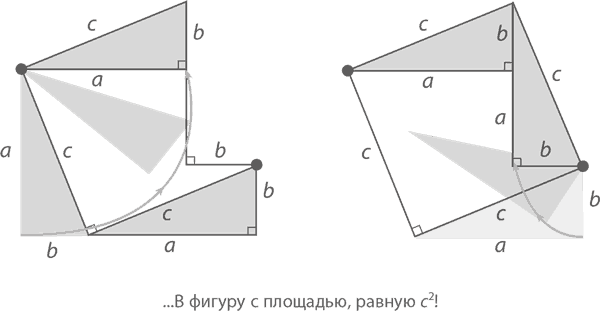
В результате получится квадрат, площадь которого будет равна c². Следовательно, a² + b² = c², что и требовалось доказать.☺

Теорема Пифагора нужна нам для того, чтобы объяснить ответ на четвертый вопрос нашей викторины – вопрос о футбольном поле и двух его воротах, расположенных в 110 метрах друг от друга, с натянутой между ними веревкой длиной 110 метров 30 сантиметров.

Расстояние от ворот до центра поля составляет 55 метров. Поднятая в этом месте вверх – до точки h – веревка дает нам прямоугольный треугольник с длиной одного катета 55 и длиной гипотенузы 55,15. Берем теорему Пифагора, добавляем немного алгебры по вкусу, перемешиваем… и получаем

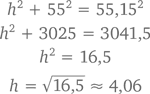
Достаточно высоко даже для самого большого грузовика, правда?